DeepMind開發用於量子化學計算的神經網路變分蒙特卡羅

編輯 | X

近百年前，狄拉克提出正電子概念，如今在醫學物理、天文物理及材料科學等多個領域都具有技術相關性。然而，正電子-分子複合物基態性質的量子化學計算具有挑戰性。

在此，DeepMind 和倫敦帝國學院的研究人員，使用最近開發的費米子神經網路 (FermiNet) 波函數來解決這個問題，該波函數不依賴基組。研究發現 FermiNet 可以在一系列具有各種不同定性正電子結合特性的原子和小分子中產生高度精確的、在某些情況下是最先進的基態能量。

研究人員計算了具有挑戰性的非極性苯分子的結合能，發現與實驗值高度一致，並得到了與使用顯式相關的高斯波函數獲得的湮滅率相比更有利的湮滅率。結果證明了基於神經網路波函數的方法的通用優勢，並將其應用於標準分子哈密頓量以外的系統。

相關研究以《Neural network variational Monte Carlo for positronic chemistry》為題，於 6 月 18 日發佈在《Nature Communications》上。

論文連結：https://www.nature.com/articles/s41467-024-49290-1隨著捕獲大量正電子實驗裝置的進步，推動了更有效率計算工具的發展，以描述正電子束縛態，加速反物質技術革新。
正電子-分子複合物基態性質的量子化學計算具有挑戰性。主要困難在於採用適當的基組來表示電子和正子之間的融合（coalescence）。
儘管正電子與電子接觸時會湮滅，但它們很容易與普通分子形成束縛態。已經有許多計算化學標準工具對正電子結合能和湮滅率進行了理論計算。但由於多種原因，描述正電子波函數仍然具有挑戰性。
在此，研究人員提出了一種計算分子正電子束縛態基態特性的新方法，該方法基於最近為 QMC 開發的神經網路波函數假設。費米子神經網路 (FermiNet) 無需參考一組基底函數即可對多體波函數進行建模。這方便地避開了上述描述正電子波函數的許多困難。
研究人員擴展了 FermiNet，以與電子分量同等地表示波函數的正電子分量。只需對神經網路架構進行最小程度的改動，就可以獲得靈活且準確的混合電子-正電子波函數假設。計算了一系列具有不同正電子結合機制的系統的正電子結合能和湮滅率，並獲得了這些系統基態能量的最高精度。
對正電子氫化物、鈉和鎂原子以及小雙原子分子的結果表明，與先前的研究相比，該方法可以達到最先進的精度。此外，對非極性二鋰和苯分子的結果表明，在描述完全由強電子-正電子關聯效應控制的正電子結合模式時，這種精度得以保留。
下圖提供了對非極性分子和正電子之間結合機制的直觀理解：關聯主導的結合是由遠離分子原子核的電子密度增加的中心促進的。在雙鋰中，這是共價鍵；在苯中，這是由於環中 π 鍵的離域而導致的分子中心電子密度的增加。

圖示：正電子鋰和苯的基態單粒子密度。 （資料來源：論文）此方法得到的苯的正電子結合能與實驗值和英國女王大學 Hofierka 等人的多體理論非常接近。而得到的湮沒率與鹼金屬原子和小分子的高精度 ECG-SVM 計算結果相當。此外，使用FermiNet 波函數累積的正電子原子和分子的2γ 湮滅率與透過其他各種計算方法獲得的結果相比較，如下表所示：
表：與透過其他各種計算方法獲得的湮滅率相比，使用FermiNet 波函數累積的正電子原子和分子的2γ 湮滅率。 （資料來源：論文）

1. 與其他方法比較，ECG-SVM 透過構造最能捕捉波函數的特徵來計算湮沒率。

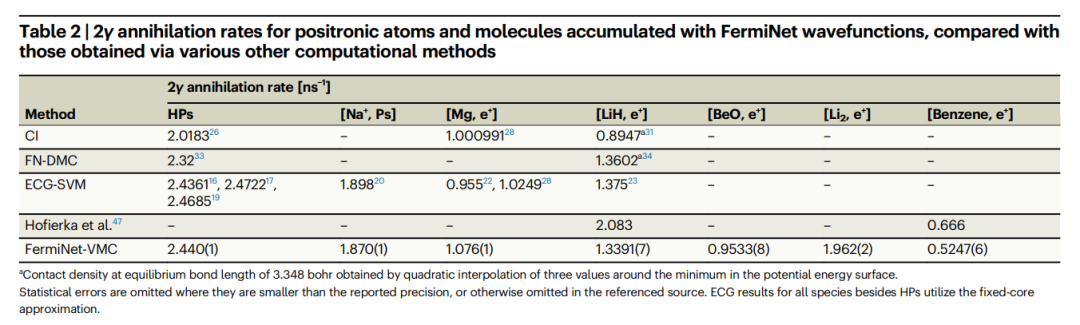
2.研究發現，對於正電子氫化物、氫化鋰和鹼金屬原子，FermiNet-VMC 和 ECG-SVM 的湮沒率結果非常一致。

3. 這表明 FermiNet-VMC 提供了準確的電子-正電子相關性描述，並且比 Hofierka 等人的多體理論結果更適合計算湮沒率。
4. 總之，ECG-SVM 方法無需系統特定的調整，即可為具有各種正電子結合機制的多種分子產生高度準確的結果。

以上是DeepMind開發用於量子化學計算的神經網路變分蒙特卡羅的詳細內容。更多資訊請關注PHP中文網其他相關文章！