Diilhamkan oleh algoritma pengoptimuman tertib pertama, pasukan Universiti Peking Lin Zhouchen mencadangkan kaedah reka bentuk untuk seni bina rangkaian saraf dengan sifat penghampiran universal

Sebagai asas teknologi pembelajaran mendalam, rangkaian saraf telah mencapai hasil yang berkesan dalam banyak bidang aplikasi. Dalam amalan, seni bina rangkaian boleh menjejaskan kecekapan pembelajaran dengan ketara Seni bina rangkaian saraf yang baik boleh menggabungkan pengetahuan terdahulu tentang masalah, mewujudkan latihan rangkaian, dan meningkatkan kecekapan pengkomputeran. Pada masa ini, kaedah reka bentuk seni bina rangkaian klasik termasuk reka bentuk manual, carian seni bina rangkaian saraf (NAS) [1], dan kaedah reka bentuk rangkaian berasaskan pengoptimuman [2]. Seni bina rangkaian yang direka secara buatan seperti ResNet, dsb.; mencari struktur rangkaian terbaik dalam ruang carian melalui pencarian atau pembelajaran pengukuhan dalam kaedah reka bentuk berasaskan pengoptimuman Kaedah ini biasanya mereka bentuk rangkaian struktur dari perspektif algoritma pengoptimuman dengan fungsi objektif yang jelas. Kaedah ini mereka bentuk struktur rangkaian dari perspektif algoritma pengoptimuman sambil mereka bentuk struktur rangkaian dari perspektif algoritma pengoptimuman.

Kini, kebanyakan reka bentuk seni bina rangkaian neural klasik mengabaikan anggaran universal rangkaian - ini adalah salah satu faktor utama untuk prestasi hebat rangkaian saraf. Oleh itu, kaedah reka bentuk ini kehilangan jaminan prestasi apriori rangkaian pada tahap tertentu. Walaupun rangkaian saraf dua lapisan mempunyai sifat penghampiran sejagat apabila lebar cenderung kepada infiniti [3], dalam praktiknya, kita biasanya hanya boleh mempertimbangkan struktur rangkaian dengan lebar terhad, dan hasil analisis prestasi dalam bidang ini sangat terhad. Sebenarnya, adalah sukar untuk mempertimbangkan sifat penghampiran universal dalam reka bentuk rangkaian, sama ada reka bentuk buatan heuristik atau carian seni bina rangkaian neural kotak hitam. Walaupun reka bentuk rangkaian saraf berasaskan pengoptimuman agak lebih boleh ditafsir, ia biasanya memerlukan fungsi objektif yang jelas, yang menghasilkan pelbagai struktur rangkaian yang direka bentuk dan mengehadkan skop aplikasinya. Cara mereka bentuk secara sistematik seni bina rangkaian saraf dengan sifat penghampiran universal kekal menjadi isu penting.

Pasukan Profesor Lin Zhouchen dari Universiti Peking mencadangkan seni bina rangkaian saraf berdasarkan alat reka bentuk algoritma pengoptimuman Kaedah ini meningkatkan kelajuan latihan dengan menggabungkan algoritma pengoptimuman tertib pertama berasaskan kecerunan dengan tertib kedua berasaskan cincang. algoritma pengoptimuman dan prestasi penumpuan, dan meningkatkan jaminan kekukuhan rangkaian saraf. Modul rangkaian saraf ini juga boleh digunakan dengan kaedah reka bentuk rangkaian berasaskan modulariti sedia ada dan terus meningkatkan prestasi model. Baru-baru ini, mereka menganalisis sifat penghampiran persamaan pembezaan rangkaian saraf (NODE) ​​dan membuktikan bahawa rangkaian saraf bersambung lapisan silang mempunyai sifat penghampiran universal Mereka juga menggunakan rangka kerja yang dicadangkan untuk mereka bentuk rangkaian varian seperti ConvNext dan ViT, dan mencapai hasil. yang melebihi garis dasar. Kertas kerja itu diterima oleh TPAMI, jurnal kecerdasan buatan teratas. . Kaedah Pengenalan

Kaedah reka bentuk rangkaian neural berasaskan pengoptimuman tradisional selalunya bermula daripada fungsi objektif dengan ungkapan eksplisit, menggunakan algoritma pengoptimuman khusus untuk menyelesaikannya, dan kemudian memetakan hasil pengoptimuman kepada struktur rangkaian saraf, seperti LISTA yang terkenal - NN ialah ungkapan eksplisit yang diperoleh dengan menggunakan algoritma LISTA untuk menyelesaikan masalah LASSO, dan mengubah keputusan pengoptimuman kepada struktur rangkaian saraf [4]. Kaedah ini mempunyai pergantungan yang kuat pada ekspresi eksplisit fungsi objektif, jadi struktur rangkaian yang terhasil hanya boleh dioptimumkan untuk ekspresi eksplisit fungsi objektif, dan terdapat risiko untuk mereka bentuk andaian yang tidak sesuai dengan keadaan sebenar. Sesetengah penyelidik cuba mereka bentuk struktur rangkaian dengan menyesuaikan fungsi objektif dan kemudian menggunakan kaedah seperti pengembangan algoritma, tetapi mereka juga memerlukan andaian seperti pengikatan semula berat yang mungkin tidak semestinya memenuhi andaian dalam situasi sebenar. Oleh itu, beberapa penyelidik telah mencadangkan menggunakan algoritma evolusi berdasarkan rangkaian saraf untuk mencari seni bina rangkaian bagi mendapatkan struktur rangkaian yang lebih munasabah.

• Format pelan reka bentuk seni bina rangkaian yang dikemas kini harus mengikut idea ​​dari algoritma pengoptimuman tertib pertama kepada algoritma titik yang lebih dekat dan menjalankan pengoptimuman secara beransur-ansur. Sebagai contoh, algoritma sudut Euler boleh ditukar kepada algoritma kuaternion, atau algoritma lelaran yang lebih cekap boleh digunakan untuk menganggarkan penyelesaian. Format yang dikemas kini harus mempertimbangkan untuk meningkatkan ketepatan pengiraan dan meningkatkan kecekapan operasi.

di mana 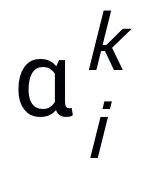dan 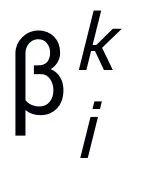mewakili pekali (saiz langkah) pada kemas kini langkah ke-k, dan kemudian menggantikan istilah kecerunan dengan modul yang boleh dipelajari T dalam rangkaian saraf untuk mendapatkan rangka rangkaian saraf lapisan L:



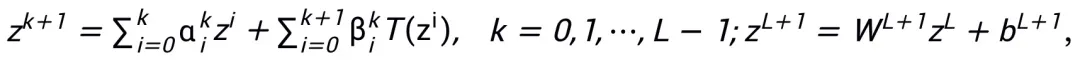
Rangka kerja kaedah keseluruhan ditunjukkan dalam Rajah 1. . terhad kepada fungsi objektif tertentu.



Pemilihan modul dan butiran seni bina

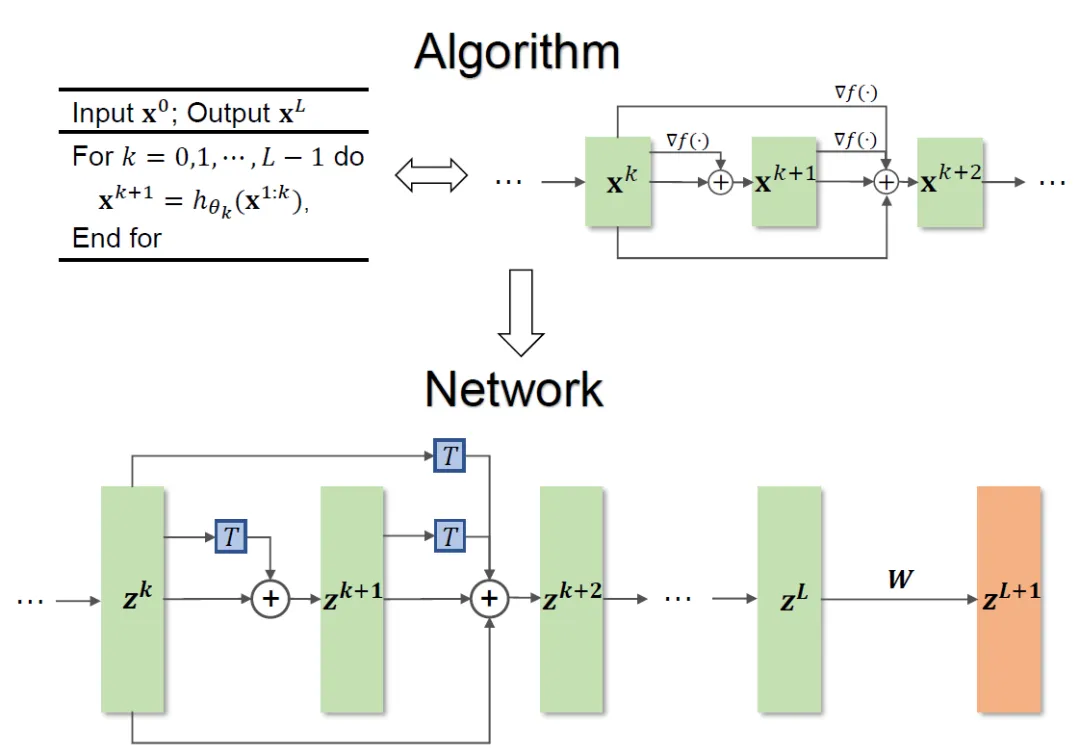
Modul rangkaian T yang direka oleh kaedah ini hanya memerlukan struktur rangkaian dua lapisan, iaitu

, sebagai substrukturnya, ia dapat memastikan bahawa rangkaian mempunyai sifat penghampiran universal, di mana

lebar lapisan yang dinyatakan adalah terhad (iaitu, ia tidak berkembang dengan peningkatan ketepatan anggaran), sifat penghampiran universal keseluruhan rangkaian tidak diperoleh dengan meluaskan lapisan. Modul T boleh menjadi blok pra-pengaktifan yang digunakan secara meluas dalam ResNet, atau ia boleh menjadi perhatian + struktur lapisan suapan dalam Transformer. Fungsi pengaktifan dalam T boleh menjadi fungsi pengaktifan biasa seperti ReLU, GeLU, Sigmoid, dll. Lapisan normalisasi yang sepadan juga boleh ditambah mengikut tugas tertentu. Selain itu, apabila

, rangkaian yang direka bentuk ialah rangkaian tersirat [5], dan kaedah lelaran titik tetap boleh digunakan untuk menghampiri format tersirat, atau kaedah pembezaan tersirat boleh digunakan untuk menyelesaikan kecerunan untuk kemas kini. 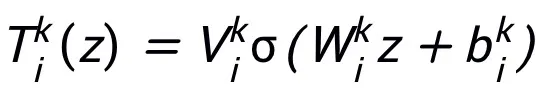Buat lebih banyak rangkaian melalui perwakilan yang setara. Kaedah ini tidak memerlukan algoritma yang sama hanya dapat sesuai dengan satu struktur. seni bina , mencerminkan fleksibilitinya. Sebagai contoh, kaedah pengganda arah selang seli linear sering digunakan untuk menyelesaikan masalah pengoptimuman yang terhad: 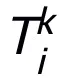Dengan membiarkan 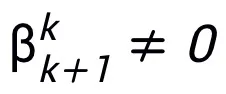kita boleh mendapatkan format lelaran yang dikemas kini yang boleh memberi inspirasi kepada rangkaian:

Struktur rangkaian

diilhamkan Lihat Rajah 2. .

Seni bina rangkaian yang direka oleh kaedah ini boleh membuktikan bahawa, di bawah syarat modul memenuhi syarat sebelumnya dan algoritma pengoptimuman (secara amnya) adalah stabil dan menumpu, rangkaian saraf yang diilhamkan oleh mana-mana algoritma pengoptimuman tertib pertama mempunyai perkara berikut ciri-ciri dalam ruang fungsi berterusan berdimensi tinggi Semua sifat penghampiran diberikan, dan kelajuan penghampiran diberikan. Buat pertama kalinya, kertas kerja membuktikan sifat penghampiran universal rangkaian saraf dengan sambungan rentas lapisan umum di bawah tetapan lebar terhad (penyelidikan terdahulu pada asasnya tertumpu pada FCNN dan ResNet, lihat Jadual 1 Teorem utama kertas itu). diterangkan secara ringkas seperti berikut:

Teorem utama (versi pendek): Biarkan 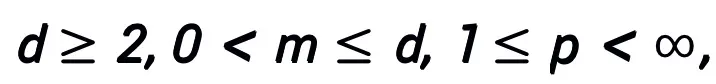A menjadi algoritma pengoptimuman tertib pertama kecerunan. Jika algoritma A mempunyai format kemas kini dalam formula (1) dan memenuhi keadaan penumpuan (pilihan saiz langkah biasa untuk algoritma pengoptimuman semuanya memenuhi keadaan penumpuan. Jika semuanya boleh dipelajari dalam rangkaian heuristik, keadaan ini tidak diperlukan), saraf rangkaian yang diilhamkan oleh algoritma:



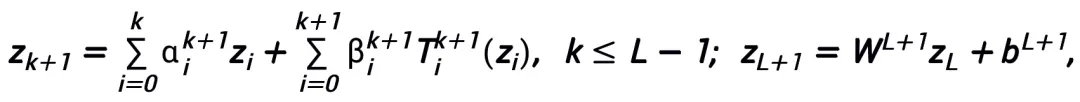
mempunyai sifat penghampiran universal di bawah ruang fungsi berterusan (bernilai vektor) 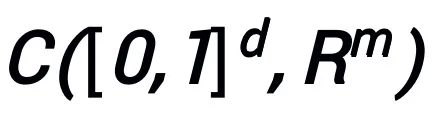dan norma 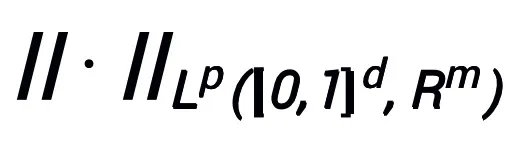sahaja, di mana struktur modul A yang boleh dipelajari sahaja dengan bentuk lapisan seperti (σ boleh menjadi fungsi pengaktifan yang biasa digunakan) boleh digunakan sebagai substrukturnya.

Struktur T yang biasa digunakan ialah:

1) Dalam rangkaian konvolusi, blok pra-pengaktifan: BN-ReLU-Conv-BN-ReLU-Conv (z),

2) Att Transformer : (z) + MLP (z+Attn (z)). Bukti teorem utama menggunakan sifat penghampiran universal NODE dan sifat penumpuan kaedah berbilang langkah linear adalah untuk membuktikan rangkaian yang diilhamkan oleh reka bentuk algoritma pengoptimuman. Struktur sepadan dengan pendiskretan NODE berterusan dengan kaedah berbilang langkah linear konvergen, oleh itu rangkaian yang diilhamkan "mewarisi" keupayaan penghampiran NODE. Dalam buktinya, kertas itu juga memberikan kelajuan anggaran NODE untuk menganggarkan fungsi berterusan dalam ruang dimensi-d, menyelesaikan masalah baki kertas sebelumnya [6].

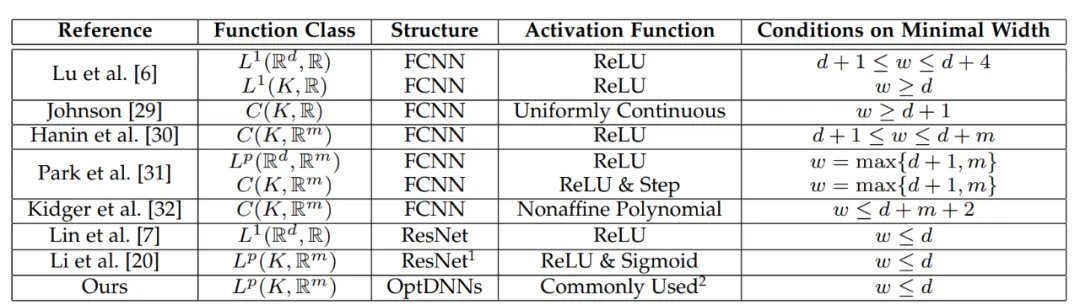Jadual 1 Penyelidikan terdahulu tentang sifat penghampiran universal pada asasnya tertumpu pada FCNN dan ResNet

Hasil eksperimen

Kertas ini menggunakan rangka kerja rangkaian dan rangkaian implisit yang dicadangkan (dipanggil OptDNN), maklumat rangkaian ditunjukkan dalam Jadual 2, dan eksperimen telah dijalankan ke atas masalah seperti pemisahan cincin bersarang, penghampiran fungsi dan klasifikasi imej. Kertas kerja ini juga menggunakan ResNet, DenseNet, ConvNext dan ViT sebagai garis dasar, menggunakan kaedah yang dicadangkan untuk mereka bentuk OptDNN yang dipertingkatkan, dan menjalankan eksperimen tentang masalah pengelasan imej, dengan mengambil kira dua penunjuk ketepatan dan FLOP.

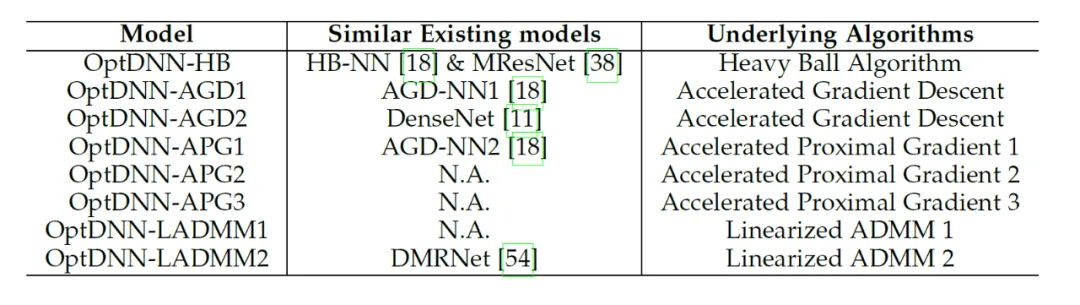Jadual 2 Maklumat berkaitan rangkaian yang direka bentuk

Pertama, OptDNN menjalankan eksperimen ke atas dua masalah: pemisahan cincin bersarang dan anggaran fungsi untuk mengesahkan sifat penghampiran universalnya. Dalam masalah penghampiran fungsi, fungsi pariti penghampiran dan fungsi Talgarsky dianggap masing-masing yang pertama boleh dinyatakan sebagai masalah klasifikasi binari, dan yang terakhir adalah masalah regresi kedua-dua masalah sukar untuk dianggarkan oleh rangkaian cetek. Keputusan eksperimen OptDNN dalam pemisahan cincin bersarang ditunjukkan dalam Rajah 3, dan keputusan eksperimen dalam anggaran fungsi ditunjukkan dalam Rajah 3. OptDNN bukan sahaja mencapai keputusan pemisahan/penghampiran yang baik, tetapi juga mencapai keputusan yang lebih besar daripada ResNet sebagai garis dasar selang klasifikasi dan ralat regresi yang lebih kecil sudah cukup untuk mengesahkan sifat penghampiran universal OptDNN.



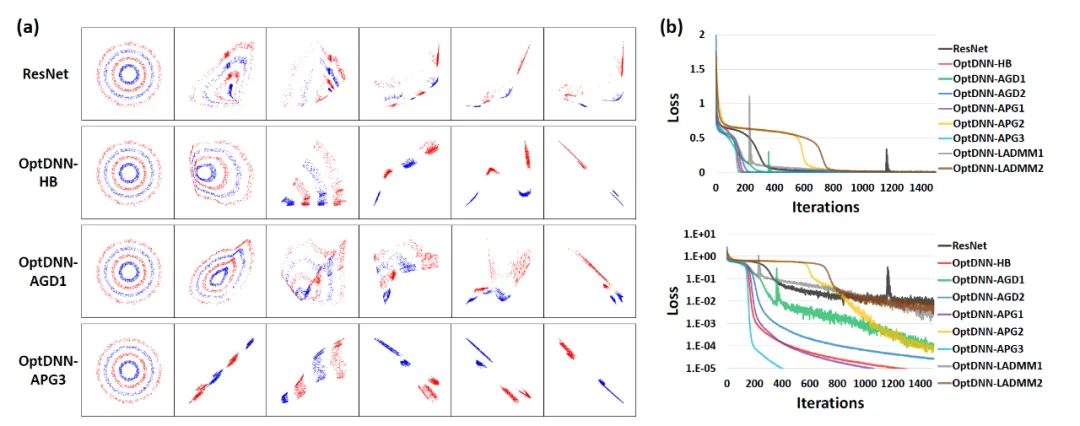
Figure 3 OPTNN Menghampiri fungsi pariti






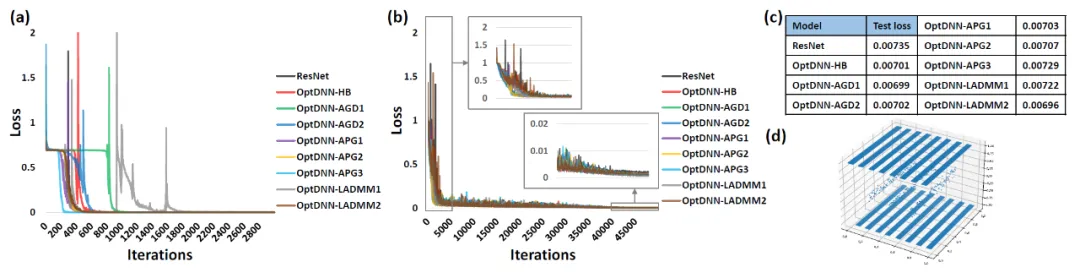
Figure 4 OPTNN Menghirakan fungsi Talgarsky kemudian, OPTDNN melakukan di CIF di bawah tetapan yang luas dan sempit masing-masing . AR Satu eksperimen mengenai tugas pengelasan imej telah dijalankan pada set data, dan hasilnya ditunjukkan dalam Jadual 3 dan 4. Percubaan semuanya dijalankan di bawah tetapan penambahan data yang kukuh. Dapat dilihat bahawa sesetengah OptDNN mencapai kadar ralat yang lebih kecil daripada ResNet pada overhed FLOP yang sama atau lebih kecil. Kertas kerja itu juga menjalankan eksperimen di bawah tetapan ResNet dan DenseNet dan mencapai keputusan percubaan yang serupa.

Table 3 Hasil eksperimen optdnn di bawah tetapan punca lebar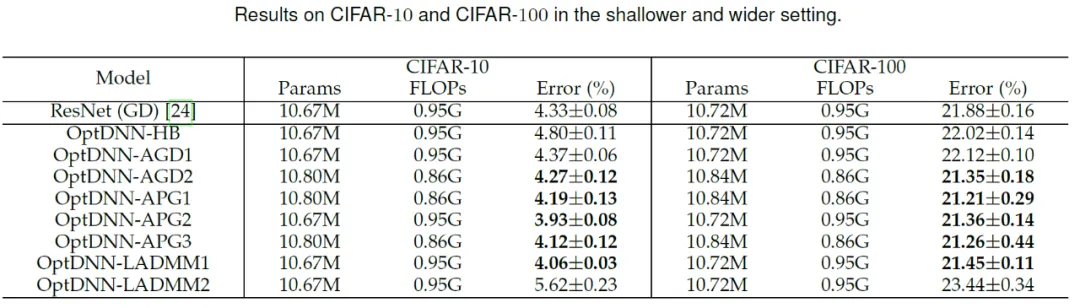

Table 4 Hasil eksperimen optdnn di bawah tetapan sempit dalam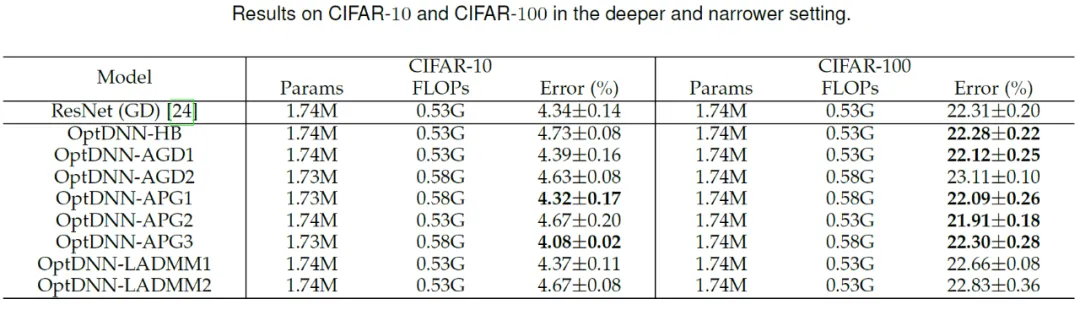

Kertas selanjutnya memilih prestasi sebelumnya yang lebih baik optdnn- Rangkaian APG2 telah diuji selanjutnya pada set data ImageNet di bawah tetapan ConvNext dan ViT Struktur rangkaian OptDNN-APG2 ditunjukkan dalam Rajah 5, dan keputusan eksperimen adalah dalam Jadual 5 dan 6. OptDNN-APG2 mencapai kadar ketepatan melebihi ConvNext dan ViT lebar yang sama, seterusnya mengesahkan kebolehpercayaan kaedah reka bentuk seni bina ini.

Rajah 5 Struktur rangkaian OptDNN-APG2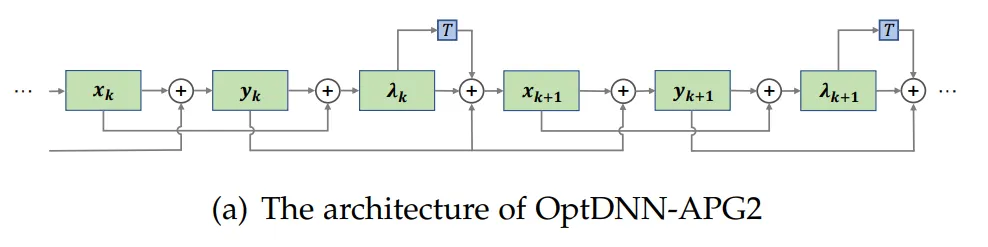

Perbandingan prestasi OptDNN-APG2 pada ImageNet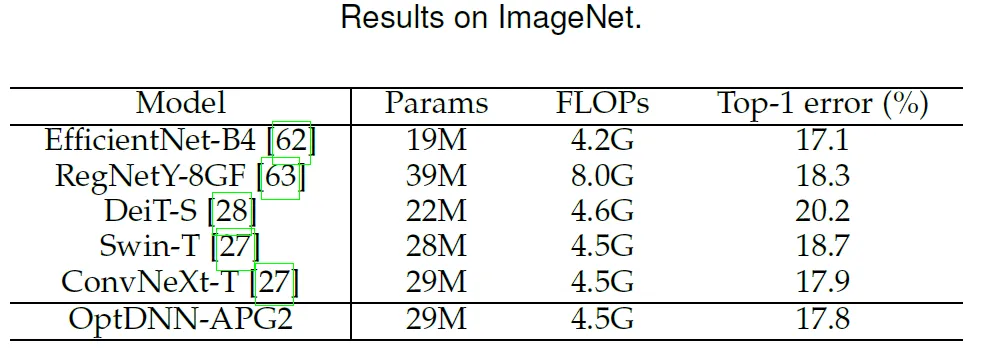

6 OptDNN-AP G2 dan isotropik ) Perbandingan prestasi of ConvNeXt dan ViT

Akhir sekali, kertas kerja itu mereka bentuk 3 rangkaian tersirat berdasarkan algoritma seperti Proximal Gradient Descent dan FISTA, dan melakukan eksperimen pada set data CIFAR dengan ResNet eksplisit dan beberapa rangkaian tersirat yang biasa digunakan Sebagai perbandingan, keputusan percubaan ditunjukkan dalam Jadual 7. Ketiga-tiga rangkaian tersirat mencapai keputusan percubaan yang setanding dengan rangkaian tersirat lanjutan, yang juga menggambarkan fleksibiliti kaedah tersebut.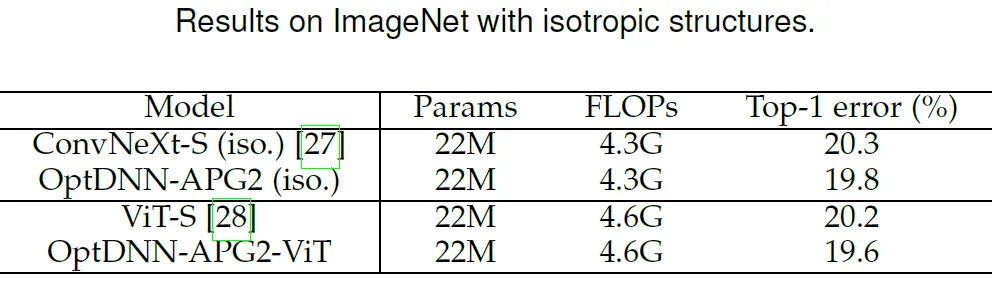

Jadual 7 Perbandingan prestasi rangkaian tersirat

Ringkasan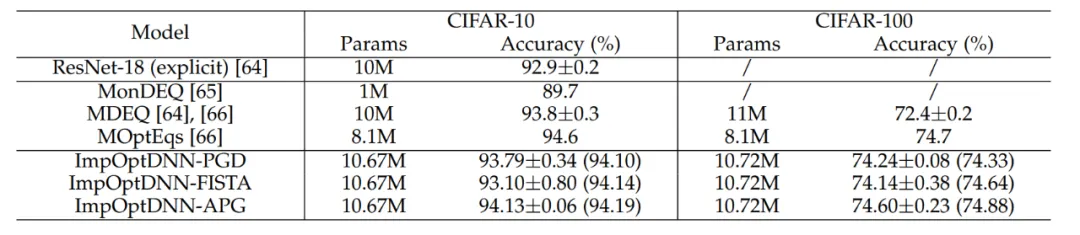

Reka bentuk seni bina rangkaian saraf merupakan salah satu isu teras dalam pembelajaran mendalam. Makalah ini mencadangkan rangka kerja bersatu untuk menggunakan algoritma pengoptimuman tertib pertama untuk mereka bentuk seni bina rangkaian saraf dengan sifat penghampiran universal, dan mengembangkan kaedah berdasarkan paradigma seni bina rangkaian reka bentuk pengoptimuman. Kaedah ini boleh digabungkan dengan kebanyakan kaedah reka bentuk seni bina sedia ada yang memfokuskan pada modul rangkaian, dan model yang cekap boleh direka bentuk dengan hampir tiada peningkatan dalam usaha pengiraan. Secara teori, kertas itu membuktikan bahawa seni bina rangkaian yang disebabkan oleh algoritma pengoptimuman konvergen mempunyai sifat penghampiran universal di bawah keadaan sederhana, dan merapatkan keupayaan perwakilan NODE dan rangkaian sambungan rentas lapisan umum. Kaedah ini juga dijangka akan digabungkan dengan NAS, reka bentuk seni bina SNN dan bidang lain untuk mereka bentuk seni bina rangkaian yang lebih cekap.

Atas ialah kandungan terperinci Diilhamkan oleh algoritma pengoptimuman tertib pertama, pasukan Universiti Peking Lin Zhouchen mencadangkan kaedah reka bentuk untuk seni bina rangkaian saraf dengan sifat penghampiran universal. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!