Bolehkah AI menakluki teorem terakhir Fermat? Ahli matematik melepaskan 5 tahun kerjayanya untuk mengubah 100 halaman bukti menjadi kod

Teorem Terakhir Fermat bakal ditakluki oleh AI?

Dan bahagian yang paling bermakna dari keseluruhannya ialah Teorem Terakhir Fermat yang akan diselesaikan oleh AI adalah tepat untuk membuktikan bahawa AI tidak berguna.

Dulu, matematik tergolong dalam alam kecerdasan manusia tulen kini, wilayah ini dihuraikan dan diinjak oleh algoritma canggih.

Gambar

Teorem Terakhir Fermat ialah teka-teki "terkenal" yang telah membingungkan ahli matematik selama berabad-abad.

Ia telah dibuktikan pada tahun 1993, dan kini, ahli matematik mempunyai rancangan yang hebat: menggunakan komputer untuk menghasilkan semula proses pembuktian.

Mereka berharap dalam versi pembuktian ini, jika terdapat sebarang kesilapan logik, ia boleh disemak oleh komputer.

Alamat projek: https://github.com/riccardobrasca/flt3

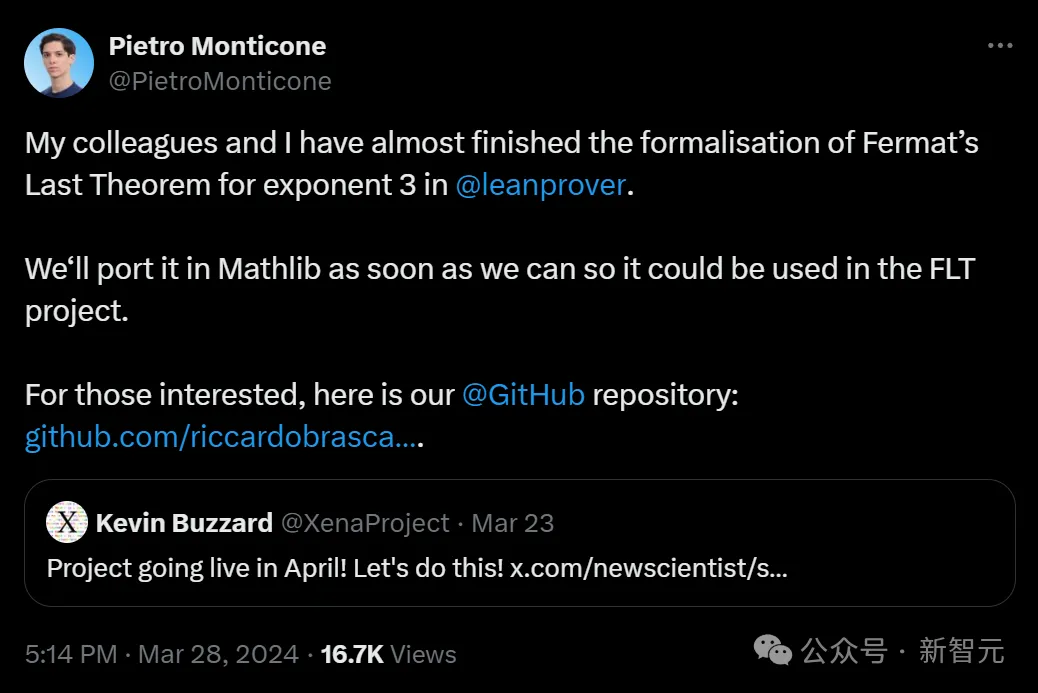
Pada penghujung bulan Mac, ahli matematik Pietro Monticone berkata dengan penuh teruja bahawa dia dan rakan sekerjanya dalam bidang Formalitas 3 hampir selesai. daripada Teorem Terakhir.

Mereka akan memindahkan proses rasmi ke Mathlib secepat mungkin untuk digunakan dalam projek FLT.

Gambar

Proses pembuktian secara kasarnya mengikut pembuktian Wiles, tetapi dengan sedikit perubahan.

Gunakan Lean untuk menukar Teorem Terakhir Fermat menjadi kod

Apabila tiba bulan April, ahli matematik dan pengaturcara Kevin Buzzard akan mengeluarkan pelan ini: untuk melengkapkan bukti Teorem Terakhir Fermat melalui kod komputer.

Selepas projek disiarkan dalam talian pada bulan April, pelan tindakan awam akan muncul dalam talian Pada masa itu, sesiapa sahaja dalam komuniti Lean boleh membuat sumbangan mereka sendiri kepada bukti rasmi.

Gambar

Mengubah bukti matematik 100 muka surat yang inovatif kepada kod komputer Adakah proses ini mudah dilaksanakan?

Ini sudah tentu terima kasih kepada alat bukti Lean, yang sangat dipuji dan ketagih untuk digunakan oleh Terence Tao, yang membolehkan pengguna menukar bukti gaya prosa kepada peraturan dan logik untuk ujian.

Pictures

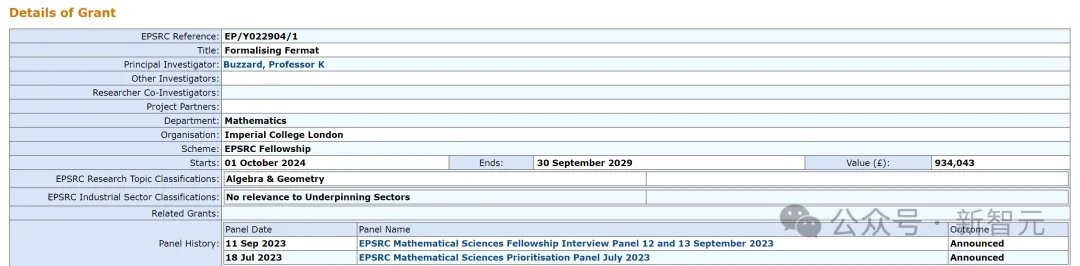
Walau bagaimanapun, projek ini tidak mudah dan dijangka mengambil masa bertahun-tahun, dan Kevin Buzzard Page memperoleh sokongan kewangan untuk projek itu.

Gambar

Semua orang faham bahawa projek ini mungkin salah satu demonstrasi berkomputer yang paling kompleks setakat ini.

Gambar

Teorem Terakhir Fermat

Teorem Terakhir Fermat ialah teka-teki matematik paling menarik dalam sejarah.

Proses membuktikan Teorem Terakhir Fermat secara langsung adalah sejarah matematik.

Gambar

Teorem Terakhir Fermat yang biasa dicadangkan oleh ahli matematik Perancis abad ke-17 Pierre de Fermat. Malangnya, dia tidak dapat mencari bukti semasa hayatnya.

Jadi, masalah yang berpunca lebih daripada 300 tahun yang lalu telah mencabar manusia secara langsung selama tiga abad, mengejutkan dunia berkali-kali, meletihkan tenaga kebanyakan otak manusia yang paling hebat, dan mempesonakan beribu-ribu orang amatur.

Gambar

Teorem ini mendakwa bahawa tiada tiga integer positif a, b, c yang memenuhi persamaan (a^n + b^n = c^n), dengan n ialah sebarang integer lebih besar daripada 2 .

Kesukaran pembuktian ini ialah sukar bagi ahli matematik untuk mencari kes negatif: Bagaimana kita boleh menjamin bahawa tidak ada integer tak terhingga n yang boleh memenuhi persamaan ini?

Gambar

Nasib baik, bagi ahli matematik hari ini, menukar konsep infiniti kepada logik bukanlah perkara baharu.

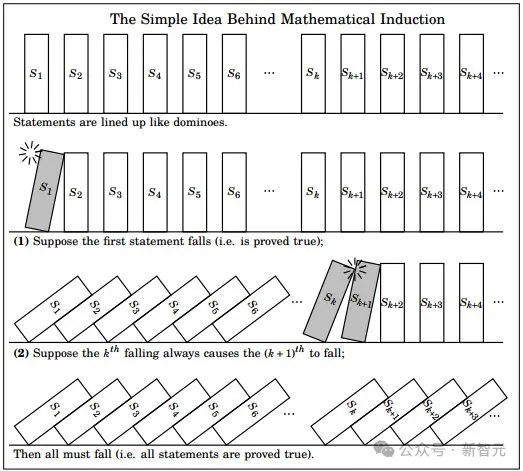
Dalam pembuktian yang lebih mudah, kita boleh bergantung pada aruhan -

Setelah logik tertentu benar untuk nombor tertentu (seperti 8), maka ia akan menjadi benar untuk setiap nombor berikutnya (seperti 9, 10). , 11, dsb.) adalah sama benar sehingga infiniti.

Gambar

Walau bagaimanapun, Teorem Terakhir Fermat telah menjadi batu penghalang dalam dunia matematik selama beratus-ratus tahun.

Pada tahun 1993 barulah ahli matematik British Andrew Wiles menyelesaikan misteri ini dengan bukti bertulis setebal 100 muka surat.

Gambar

Mengapa komputer tidak boleh membuktikan Teorem Terakhir Fermat?

Industri percaya bahawa terdapat tiga sebab:

1. Komputer tidak dapat menyimpulkan spesis yang tidak terhingga s boleh muncul Kesilapan sekejap

Nasib baik, ada bukti tambahan Lean

Bukti matematik 100 muka surat tidak begitu mudah dikawal, sama ada untuk pelajar matematik biasa atau ahli matematik.

Nasib baik, kita tidak boleh lagi bergantung pada kaedah bukti tradisional dan boleh beralih kepada alat seperti Lean.

Ia adalah alat pengaturcaraan yang dibangunkan berdasarkan C++, direka khas untuk menulis dan mengesahkan bukti induksi.

Banyak daripada apa yang dipanggil "kecerdasan buatan" hari ini tidak lebih daripada perkataan yang disusun dengan bijak yang meniru bahasa manusia. Tetapi bukti berbantukan komputer seperti Lean lebih menyepadukan pemikiran manusia dan keupayaan dipertingkatkan berbantukan komputer. .

Melalui alatan ini, pelajar boleh memecahkan kandungan yang dibincangkan dalam kelas kepada langkah-langkah operasi logik dan matematik.

Ini seperti Batu Rosetta pembuktian matematik.

Clarissa Littler, yang juga seorang guru matematik, sangat bersetuju dengan falsafah Kevin Buzzard.

Dia mengajar matematik diskret di Kolej Komuniti Portland. Dalam dua semester yang lalu, dia telah menggunakan "Permainan Pengenalan Klasik Lean" yang dibangunkan oleh Kevin Buzzard dalam kelas matematik diskretnya.

Gambar

Alamat: https://adam.math.hhu.de/

Dia akan menggunakan "Permainan Nombor Asli" untuk membantu pelajar membiasakan diri dengan idea induksi matematik, dan melalui "Permainan Teori Set", dia akan membiasakan mereka membuat penaakulan tentang set.

Gambar

Dalam proses ini, jurang pemahaman pelajar antara "mengikut peraturan logik untuk menulis bukti dengan ketat" dan "menggunakan bahasa popular untuk menerangkan kebenaran sesuatu" akan dirapatkan secara beransur-ansur.

Littler menekankan bahawa fokus utama kursus ini adalah untuk membolehkan pelajar yang mempunyai asas matematik yang lemah untuk berfikir dengan lebih bebas mengikut cara ahli matematik, pada masa yang sama lebih memahami bukti, bukti dan kaedah menunjukkan kebenaran.

Peralihan daripada logik formal kepada senarai peraturan kepada ungkapan dalam prosa adalah kunci untuk memecahkan projek kepada kepingan kod yang bekerjasama.

Gambar

Ini amat penting dalam persimpangan pengaturcaraan dan matematik tulen, dan di sinilah alat seperti Lean boleh bersinar.

Buzzard berkata bahawa dia berharap dapat mengubah idea matematik kompleks yang dicetuskan oleh Teorem Terakhir Fermat kepada bentuk yang boleh diprogramkan.

Selama berabad-abad lamanya, banyak cabang matematik baharu yang berharga telah dicipta untuk membuktikan teorem ini, yang pada pendapat Buzzard adalah "tiada kepentingan praktikal".

Ya, pada pandangan Buzzard, teorem terakhir Fermat tidak bermakna dan tidak mempunyai aplikasi dalam dunia nyata Namun, disebabkan masalah "terkenal" ini, banyak idea baharu yang cemerlang telah dihasilkan dalam beberapa tahun kebelakangan ini.

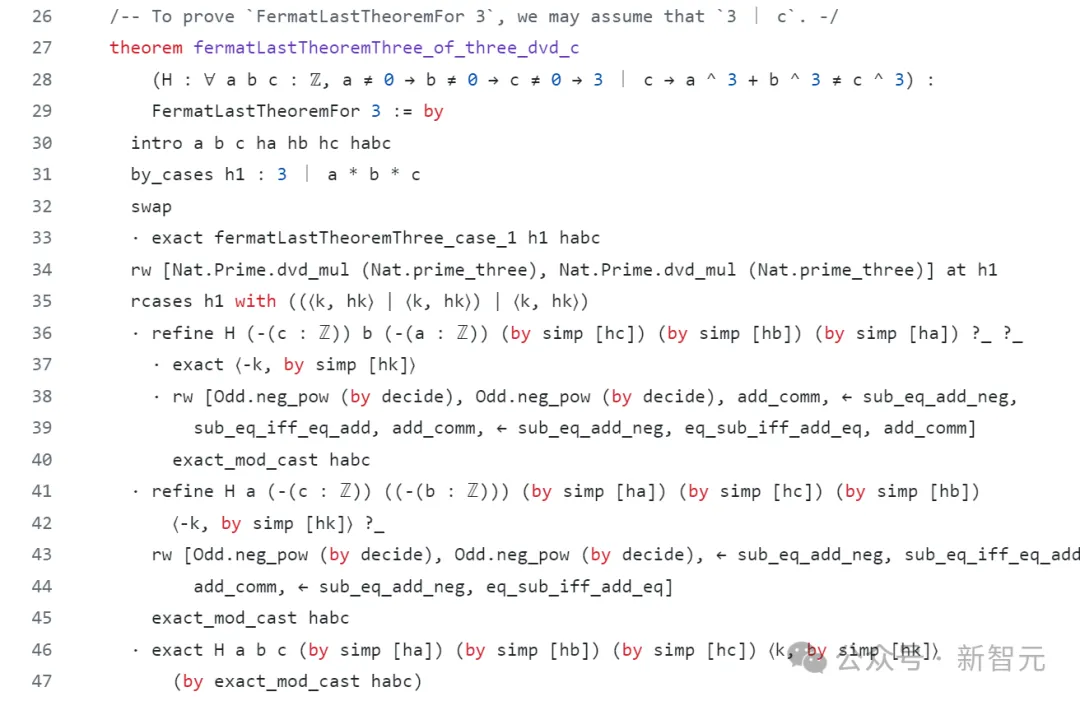
Kini, menukar bukti 100 muka surat Wiles kepada bahasa dan peraturan formal yang boleh difahami oleh komputer dijangka membuka pintu kepada bukti bantuan komputer untuk ahli matematik generasi baharu.

Gambar

Dan alat penukaran ini juga boleh membantu pengaturcara.

Littler berkata dalam bidang ini, projek bercita-cita tinggi sentiasa berbaloi untuk dicuba kerana kita semua boleh mendapat manfaat daripada pelajaran yang dipelajari dan perpustakaan yang ditulis.

Walaupun pembuktian teorem interaktif masih merupakan bidang yang agak baharu, komuniti Lean telah melakukan banyak kerja yang cemerlang.

Kevin Buzzard: Penginjil kurus

Kevin Mark Buzzard, dilahirkan pada tahun 1968, mempunyai pengetahuan profesional yang mendalam dalam geometri aritmetik dan program Langlands.

Beliau kini seorang profesor matematik tulen di Imperial College London dan "penginjil" alat AI Lean.

Semasa belajar di Royal Grammar School, Kevin Buzzard telah menyertai International Mathematical Olympiad dan memenangi pingat gangsa pada tahun 1986 dan pingat emas dengan markah sempurna pada tahun 1987.

Pictures

Selepas itu, beliau menamatkan pengajian sarjana dalam bidang matematik di Kolej Trinity, Universiti Cambridge, menerima gelaran Senior Wrangler pada tahun 1990 dan ijazah C.A.S.M.

Di bawah bimbingan Richard Taylor, tesis kedoktorannya "Tahap perwakilan modular" telah disiapkan pada tahun 1995, meneroka bidang yang kompleks dalam matematik.

Gambar

Pada tahun 1998, beliau mula bekerja sebagai pensyarah di Imperial College London, dinaikkan pangkat sebagai pensyarah kanan pada tahun 2002, dan dilantik sebagai profesor pada tahun 2004.

Beliau juga menjalankan penyelidikan lawatan di Universiti Harvard (Oktober hingga Disember 2002) dan beberapa institusi terkenal lain.

Untuk sumbangan cemerlangnya dalam bidang teori nombor, beliau memenangi Anugerah Whitehead pada tahun 2002 dan Anugerah Berwick Senior pada tahun 2008.

Pada 2017, Buzzard melancarkan projek dan blog tentang Lean Theorem Prover, khusus untuk mempromosikan penggunaan alat bukti berbantukan komputer dalam penyelidikan matematik.

Beliau juga membimbing pemuzik Dan Snaith (nama pentas Caribou) untuk menyiapkan tesis kedoktoran matematiknya mengenai kajian simbol modul super-convergen Siegel, yang mana Snaith menerima PhD dari Imperial College London.

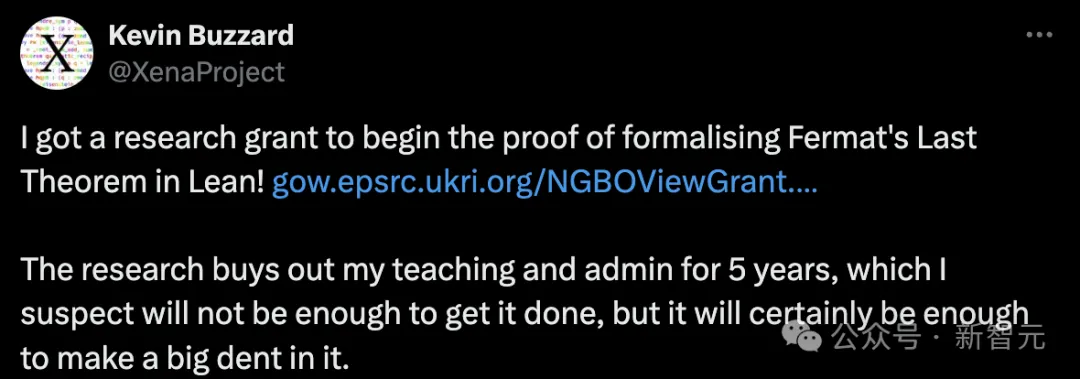
Pada Oktober 2023, Kevin Buzzard menyatakan di media sosial bahawa dia menerima pembiayaan penyelidikan dan mula menggunakan Lean untuk membuktikan Teorem Terakhir Fermat.

Gambar

Buzzard berkata, "Sepuluh tahun yang lalu, ini akan mengambil masa yang tidak terhingga." Beliau akan menangguhkan tugas mengajarnya selama lima tahun untuk menyiapkan projek itu.

Adakah berbaloi untuk menangguhkan tugas anda sendiri?

Pada pendapat rakan sekerjanya, Chris Williams dari University of Nottingham di UK, projek jenis ini mungkin mempunyai faedah yang tidak dijangka dan kesan yang meluas.

"Saya fikir tidak mungkin dia akan merasmikan keseluruhan bukti dalam tempoh lima tahun akan datang, jika tidak, ia akan menjadi menakjubkan. Walau bagaimanapun, banyak alat kini terdapat di mana-mana dalam teori nombor dan geometri aritmetik, jadi saya meramalkan bahawa masa depan Kemajuan yang besar akan sangat berguna."

Signifikan untuk penyelidikan matematik

Projek ini juga mendedahkan nilai yang lebih mendalam.

Dengan kemajuan berterusan alat pengkomputeran, sempadan antara cabang matematik yang berbeza, malah antara disiplin yang berbeza, menjadi semakin kabur, yang telah membawa kepada kemunculan beberapa bukti yang hampir mustahil untuk disahkan.

Sebagai contoh, ahli matematik Jepun Mochizuki Shinichi dari Universiti Kyoto menulis bukti 500 muka surat yang mengambil masa beberapa tahun untuk diterbitkan kerana ia sangat rumit, sebahagiannya kerana orang tidak tahu apa yang perlu dilakukan dengannya.

Mulai sekarang, kita mungkin mendapati bahawa sempadan matematik semakin kabur.

Ini tidak merujuk kepada kebenaran atau kekaburan logik, tetapi kepada julat idea berbeza yang boleh digabungkan dalam bukti.

Lean membolehkan ahli matematik menukar idea mereka kepada kod, yang memudahkan rakan sebaya untuk memahami. Melihat kepada preseden yang dicatatkan oleh pendahulu, ahli matematik masa depan boleh terus memajukan penyelidikan mereka sendiri atas dasar ini.

Buzzard berkata bahawa ciri penulisan matematik dalam Lean ialah anda boleh meninggalkan keputusan yang dinyatakan dengan tepat tetapi tidak terbukti, dan orang lain boleh menyelesaikannya kemudian.

Lean sendiri memudahkan aliran kerja sedemikian.

Gambar

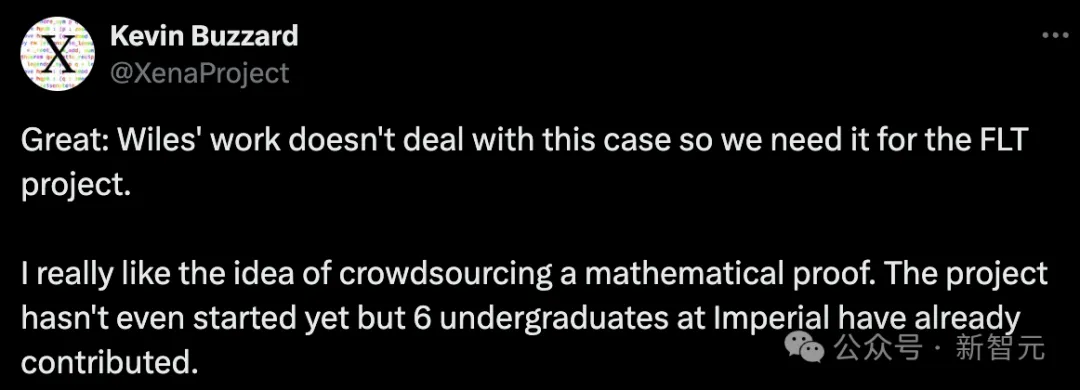
Dalam erti kata lain, teorem terakhir Fermat sedang bersedia untuk diselesaikan dengan "crowdsourcing" - terutamanya jika kerja pengekodan melebihi baki tahun bekerja Buzzard.

Melengkapkan pembuktian matematik memerlukan usaha seluruh masyarakat.

Mungkin, pada masa hadapan, kita boleh mempunyai platform yang serupa dengan Genius.com untuk berkongsi dan mentafsir bukti matematik.

Rujukan:

https://www.php.cn/link/845375903f6dbadda379558e905089f2

650 4a4a5a1e679e2eaad38b595

🎜🎜

Atas ialah kandungan terperinci Bolehkah AI menakluki teorem terakhir Fermat? Ahli matematik melepaskan 5 tahun kerjayanya untuk mengubah 100 halaman bukti menjadi kod. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!