Model besar juga boleh dihiris, dan Microsoft SliceGPT sangat meningkatkan kecekapan pengiraan LLAMA-2

Model bahasa berskala besar (LLM) biasanya mempunyai berbilion parameter dan dilatih menggunakan trilion token. Walau bagaimanapun, model sedemikian sangat mahal untuk dilatih dan digunakan. Untuk mengurangkan keperluan pengiraan, pelbagai teknik pemampatan model sering digunakan.

Teknik pemampatan model ini secara amnya boleh dibahagikan kepada empat kategori: penyulingan, penguraian tensor (termasuk pemfaktoran peringkat rendah), pemangkasan dan kuantisasi. Kaedah pemangkasan telah wujud sejak sekian lama, tetapi banyak yang memerlukan penalaan halus pemulihan (RFT) selepas pemangkasan untuk mengekalkan prestasi, menjadikan keseluruhan proses mahal dan sukar untuk skala.

Para penyelidik dari ETH Zurich dan Microsoft telah mencadangkan penyelesaian kepada masalah ini, yang dipanggil SliceGPT. Idea teras kaedah ini adalah untuk mengurangkan dimensi benam rangkaian dengan memadamkan baris dan lajur dalam matriks berat untuk mengekalkan prestasi model. Kemunculan SliceGPT menyediakan penyelesaian yang berkesan untuk masalah ini.

Para penyelidik menyatakan bahawa dengan SliceGPT, mereka dapat memampatkan model besar dalam beberapa jam menggunakan GPU tunggal, mengekalkan prestasi kompetitif dalam penjanaan dan tugas hiliran walaupun tanpa RFT. Pada masa ini, penyelidikan telah diterima oleh ICLR 2024. . 2401 .15024.pdf

Kaedah pemangkasan berfungsi dengan menetapkan elemen tertentu matriks berat dalam LLM kepada sifar dan mengemas kini elemen sekeliling secara terpilih untuk mengimbangi. Ini menghasilkan mod jarang yang melangkau beberapa operasi titik terapung dalam laluan hadapan rangkaian saraf, sekali gus meningkatkan kecekapan pengiraan.

• Tahap sparsity dan sparsity adalah faktor yang menentukan peningkatan relatif dalam kelajuan pengkomputeran. Apabila mod jarang adalah lebih munasabah, ia akan membawa lebih banyak kelebihan pengiraan. Tidak seperti kaedah pemangkasan lain, SliceGPT memangkas dengan memotong (memotong!) keseluruhan baris atau lajur matriks berat. Sebelum pemotongan semula, rangkaian mengalami transformasi yang memastikan ramalan tidak berubah tetapi membenarkan proses ricih terjejas sedikit. Hasilnya ialah matriks berat dikurangkan, penghantaran isyarat menjadi lemah, dan dimensi rangkaian saraf dikurangkan.
• Rajah 1 di bawah membandingkan kaedah SliceGPT dengan kaedah sparsity sedia ada.

Melalui eksperimen yang meluas, pengarang mendapati bahawa SliceGPT boleh mengalih keluar sehingga 25% parameter model (termasuk benam) untuk model LLAMA-2 70B, OPT-26B dan Phi 9, model padat masing-masing , 99% dan 90% prestasi tugasan sampel sifar.

Model yang diproses oleh SliceGPT boleh dijalankan pada GPU yang lebih sedikit dan lebih pantas tanpa sebarang pengoptimuman kod tambahan: pada GPU gred pengguna 24GB, pengarang mengira jumlah pengiraan inferens LLAMA-2 hingga 70B Jumlah dikurangkan kepada 64% pada model padat; pada 40GB A100 GPU, mereka mengurangkannya kepada 66%.

Selain itu, mereka juga mencadangkan konsep baharu, invarian pengiraan dalam rangkaian Transformer, yang membolehkan SliceGPT.

SliceGPT secara terperinci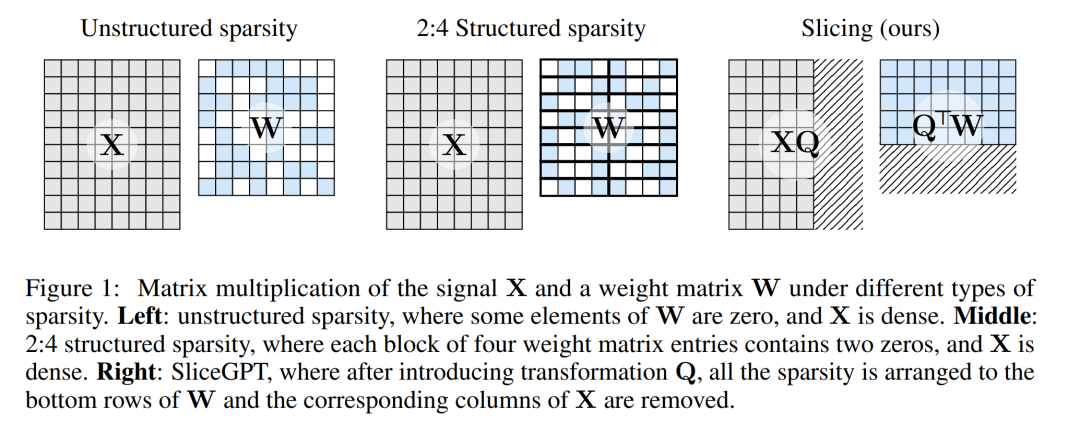

Kaedah SliceGPT bergantung pada invarian pengiraan yang wujud dalam seni bina Transformer. Ini bermakna anda boleh menggunakan transformasi ortogon pada output satu komponen dan kemudian buat asalnya dalam komponen seterusnya. Penulis memerhatikan bahawa operasi RMSNorm yang dilakukan antara blok rangkaian tidak menjejaskan transformasi: operasi ini adalah komutatif.

Dalam kertas kerja, penulis mula-mula memperkenalkan cara mencapai invarian dalam rangkaian Transformer dengan sambungan RMSNorm, dan kemudian menerangkan cara menukar rangkaian yang dilatih dengan sambungan LayerNorm kepada RMSNorm. Seterusnya, mereka memperkenalkan kaedah menggunakan analisis komponen utama (PCA) untuk mengira transformasi setiap lapisan, dengan itu mengunjurkan isyarat antara blok ke komponen utamanya. Akhir sekali, mereka menunjukkan cara mengalih keluar komponen utama kecil sepadan dengan memotong baris atau lajur rangkaian.

Invarian pengiraan rangkaian Transformer

Gunakan Q untuk mewakili matriks ortogon:

• Perhatikan bahawa mendarab vektor

Andaikan X_ℓ ialah keluaran blok transformer Selepas diproses oleh RMSNorm, ia adalah input kepada blok seterusnya dalam bentuk RMSNorm (X_ℓ). Jika anda memasukkan lapisan linear dengan matriks ortogon Q sebelum RMSNorm dan Q^⊤ selepas RMSNorm, rangkaian akan kekal tidak berubah kerana setiap baris matriks isyarat didarab dengan Q, dinormalkan dan didarab dengan Q^ ⊤. Di sini kita ada:

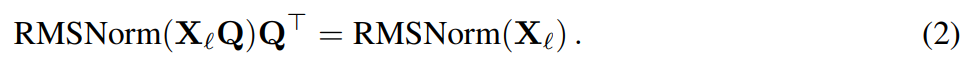
Kini, memandangkan setiap perhatian atau blok FFN dalam rangkaian melakukan operasi linear pada input dan output, operasi tambahan Q boleh diserap ke dalam lapisan linear modul. Memandangkan rangkaian mengandungi sambungan baki, Q juga mesti digunakan pada output semua lapisan sebelumnya (sehingga pembenaman) dan semua lapisan berikutnya (sehingga LM Head).

Fungsi invarian merujuk kepada fungsi yang transformasi inputnya tidak menyebabkan output berubah. Dalam contoh artikel ini, sebarang penjelmaan ortogonal Q boleh digunakan pada pemberat pengubah tanpa mengubah hasilnya, jadi pengiraan boleh dilakukan dalam sebarang keadaan penjelmaan. Penulis memanggil invarian pengiraan ini dan mentakrifkannya dalam teorem berikut.

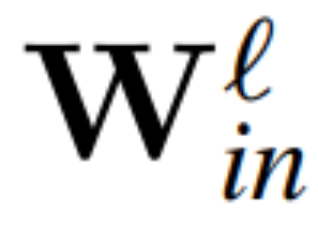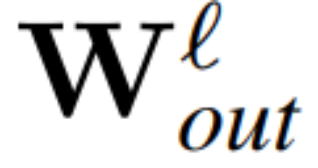Teorem 1: Biarkan dan menjadi matriks berat ℓ lapisan linear rangkaian pengubah bersambung RMSNorm, 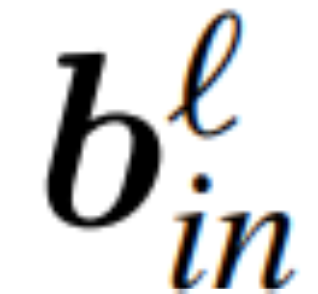dan 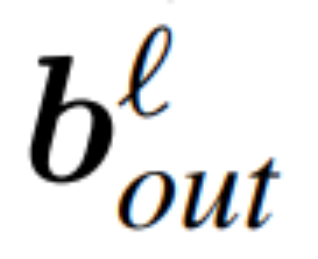menjadi pincang sepadan (jika ada), W_embd dan kepala matriks W_embd dan Wdding_head matriks . Dengan mengandaikan Q ialah matriks ortogon dengan dimensi D, maka rangkaian berikut adalah bersamaan dengan rangkaian transformer asal:

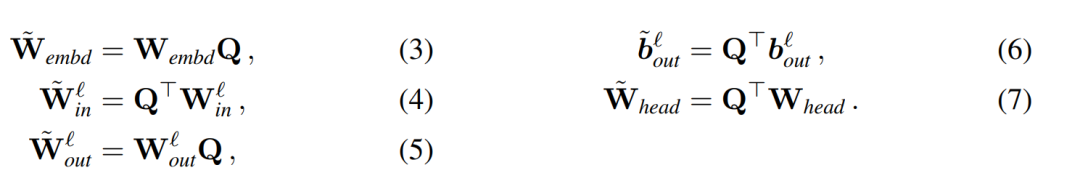
Menyalin bias input dan bias kepala:

boleh dilakukan melalui algoritma 1 untuk membuktikan bahawa rangkaian yang ditukar mengira hasil yang sama seperti rangkaian asal.

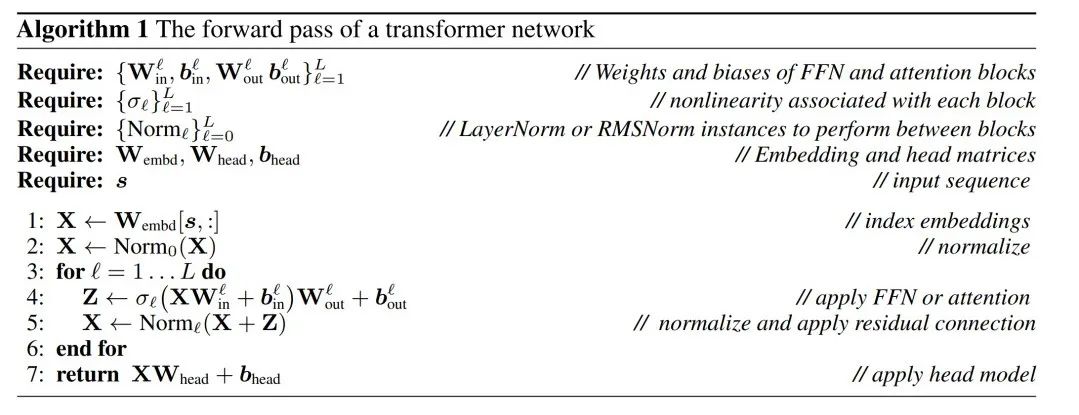
LayerNorm Transformer boleh ditukar kepada RMSNorm

Transformer Peranti pengiraan RM hanya disambungkan kepada rangkaian RMS Sebelum memproses rangkaian menggunakan LayerNorm, penulis terlebih dahulu menukar rangkaian kepada RMSNorm dengan menyerap blok linear LayerNorm ke dalam blok bersebelahan.

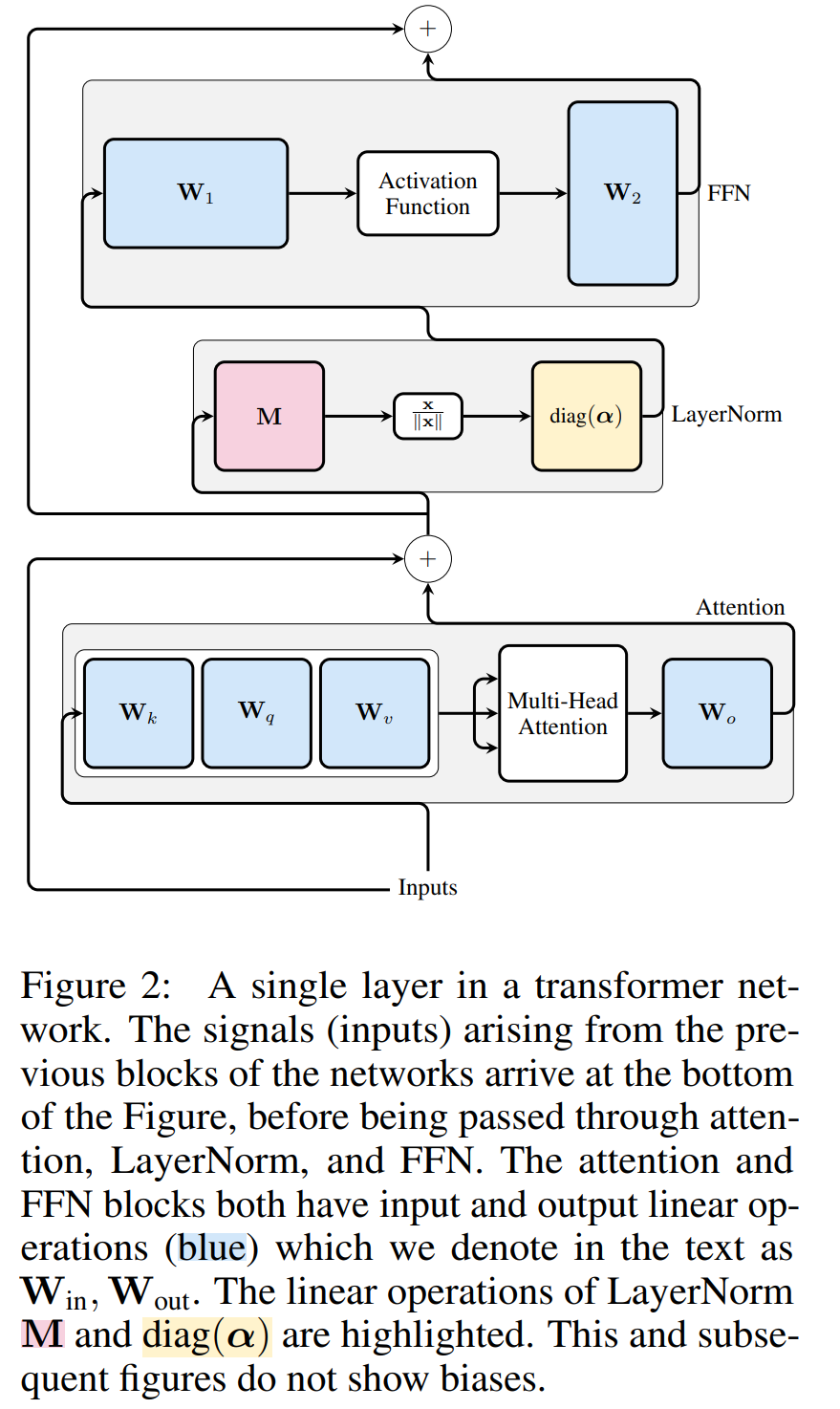
Rajah 3 menunjukkan transformasi rangkaian Transformer ini (lihat Rajah 2). Dalam setiap blok, pengarang mendarabkan matriks keluaran W_out dengan matriks tolak min M, yang mengambil kira penolakan min dalam LayerNorm berikutnya. Matriks input W_in didarabkan dengan bahagian blok LayerNorm sebelumnya. Matriks benam W_embd mesti menjalani penolakan min, dan W_head mesti diskala semula mengikut bahagian LayerNorm terakhir. Ini adalah perubahan mudah dalam susunan operasi dan tidak akan menjejaskan output rangkaian.

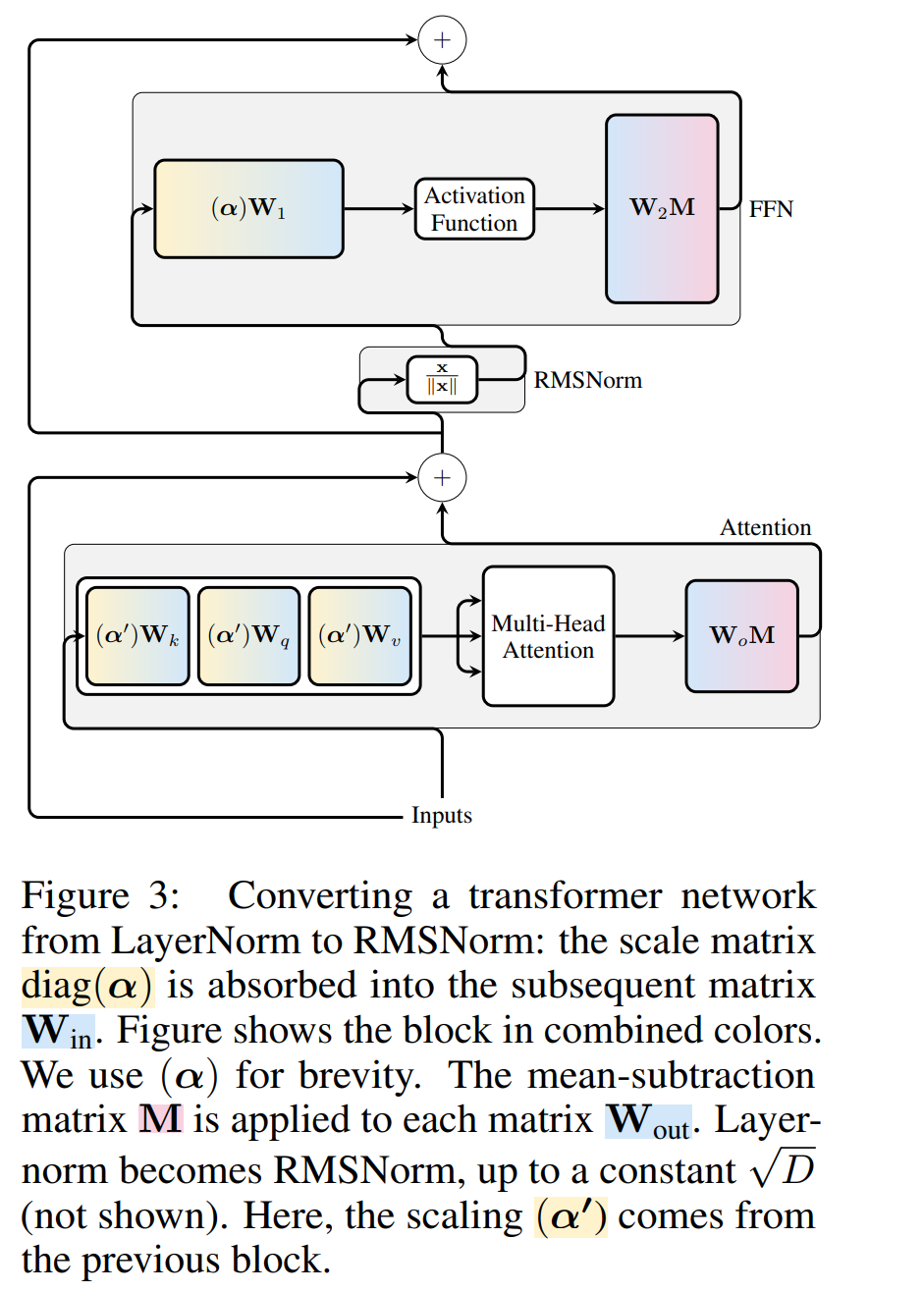
Transformasi setiap blok

Sekarang setiap LayerNorm dalam transformer telah ditukar kepada RMSNorm, mana-mana Q boleh dipilih untuk mengubah suai. Rancangan asal pengarang adalah untuk mengumpul isyarat daripada model, menggunakan isyarat ini untuk membina matriks ortogon, dan kemudian memadamkan bahagian rangkaian. Mereka dengan cepat mendapati bahawa isyarat daripada blok berbeza dalam rangkaian tidak sejajar, jadi mereka perlu menggunakan matriks ortogon yang berbeza, Q_ℓ, pada setiap blok.

Jika matriks ortogon yang digunakan dalam setiap blok adalah berbeza, model tidak akan berubah Kaedah pembuktian adalah sama dengan Teorem 1, kecuali untuk baris 5 Algoritma 1. Di sini anda boleh melihat bahawa output sambungan baki dan blok mesti mempunyai putaran yang sama. Untuk menyelesaikan masalah ini, penulis mengubah suai sambungan baki dengan menukarkan baki secara linear.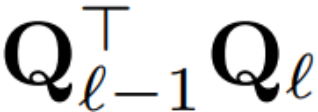

Rajah 4 menunjukkan cara melakukan putaran berbeza pada blok berbeza dengan melakukan operasi linear tambahan pada sambungan baki. Tidak seperti pengubahsuaian pada matriks berat, operasi tambahan ini tidak boleh diprakira dan menambah overhed kecil (D × D) pada model. Namun, operasi ini diperlukan untuk memotong model, dan anda dapat melihat bahawa kelajuan keseluruhan meningkat.

Untuk mengira matriks Q_ℓ, penulis menggunakan PCA. Mereka memilih set data penentukuran daripada set latihan, menjalankannya melalui model (selepas menukar operasi LayerNorm kepada RMSNorm), dan mengekstrak matriks ortogon untuk lapisan tersebut. Lebih tepat lagi, jika mereka menggunakan output rangkaian yang diubah untuk mengira matriks ortogon lapisan seterusnya. Lebih tepat lagi, jika 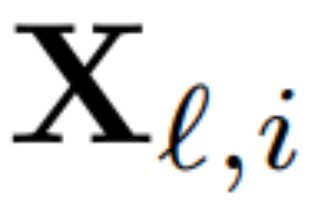ialah output modul RMSNorm ke-ℓ-th untuk jujukan ke-i dalam set data penentukuran, hitung: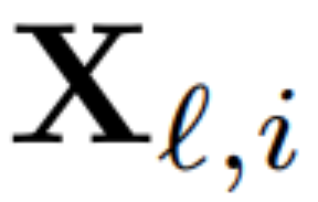

dan tetapkan Q_ℓvector bagi C_ℓ dalam nilai eigen Sort.成 Penyingkiran 分 Sasaran analisis komponen utama adalah untuk mendapatkan matriks data X dan mengira perwakilan berdimensi rendah Z dan anggaran pembinaan semula :

Antaranya Q ialah

, ialah vektor eigen. a D × D matriks pemadaman kecil (mengandungi D lajur kecil matriks homotopik D × D) digunakan untuk memadam beberapa lajur di sebelah kiri matriks. Pembinaan semula adalah L_2 optimum dalam erti kata bahawa QD ialah peta linear yang meminimumkan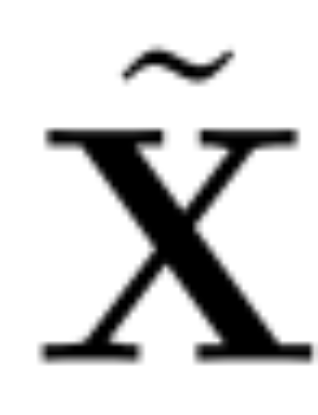

.

Apabila menggunakan PCA pada matriks isyarat antara blok Dalam operasi di atas, matriks ini telah didarab dengan Q. Pengarang mengalih keluar baris W_in dan lajur W_out dan W_embd. Mereka juga mengeluarkan baris dan lajur matriks

yang dimasukkan ke dalam sambungan baki (lihat Rajah 4).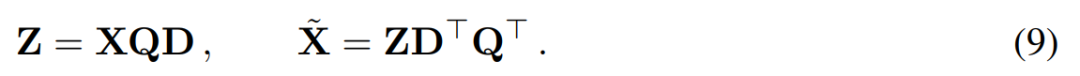

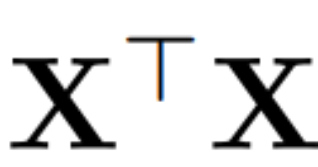
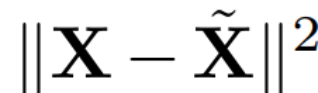Hasil eksperimen

Tugas penjanaan

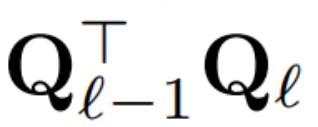
Pengarang menjalankan penilaian prestasi ke atas siri model OPT dan LLAMA-2 dengan saiz yang berbeza dan SxGPT yang dipangkas oleh Wikisett SxGPT-2. set data. Jadual 1 menunjukkan kerumitan yang dikekalkan selepas pelbagai tahap pemangkasan model. Berbanding model LLAMA-2, SliceGPT menunjukkan prestasi unggul apabila digunakan pada model OPT, yang konsisten dengan spekulasi penulis berdasarkan analisis spektrum model.

Prestasi SliceGPT akan bertambah baik apabila saiz model bertambah. Mod SparseGPT 2:4 berprestasi lebih teruk daripada SliceGPT pada keratan 25% untuk semua model siri LLAMA-2. Bagi OPT, boleh didapati bahawa sparsity model dengan nisbah resection 30% adalah lebih baik daripada 2:4 dalam semua model kecuali model 2.7B.

Tugas sampel sifar

Pengarang menggunakan lima tugasan: PIQA, WinoGrande, HellaSwag, ARC-e dan ARCc untuk menilai prestasi SliceGPT pada tugasan sampel sifar mereka menggunakan LM Evaluation Harness dalam parameter penilaian.

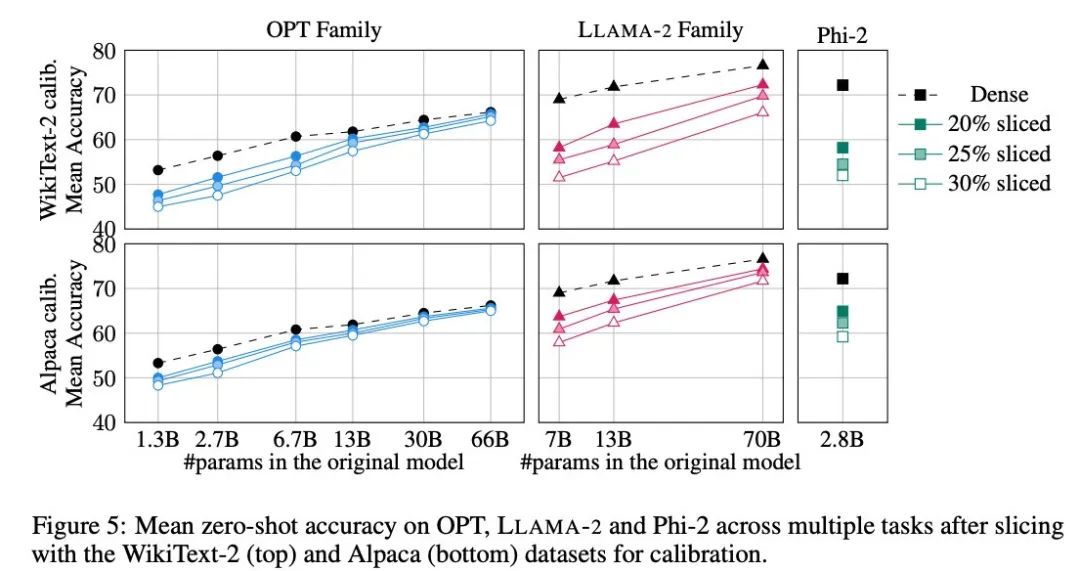
Rajah 5 menunjukkan purata markah yang dicapai oleh model yang disesuaikan pada tugasan di atas. Baris atas rajah menunjukkan ketepatan purata SliceGPT dalam WikiText-2, dan baris bawah menunjukkan ketepatan purata SliceGPT dalam Alpaca. Kesimpulan yang sama boleh diperhatikan daripada keputusan seperti dalam tugas penjanaan: model OPT lebih mudah disesuaikan dengan pemampatan daripada model LLAMA-2, dan semakin besar model, semakin kurang jelas penurunan ketepatan selepas pemangkasan.

Pengarang menguji kesan SliceGPT pada model kecil seperti Phi-2. Model Phi-2 yang dipangkas menunjukkan prestasi yang setanding dengan model LLAMA-2 7B yang dipangkas. Model OPT dan LLAMA-2 terbesar boleh dimampatkan dengan cekap, dan SliceGPT hanya kehilangan beberapa mata peratusan apabila mengeluarkan 30% daripada model OPT 66B.

Pengarang juga menjalankan eksperimen penalaan halus pemulihan (RFT). Sebilangan kecil RFT telah dilakukan pada model LLAMA-2 dan Phi-2 yang dipangkas menggunakan LoRA.

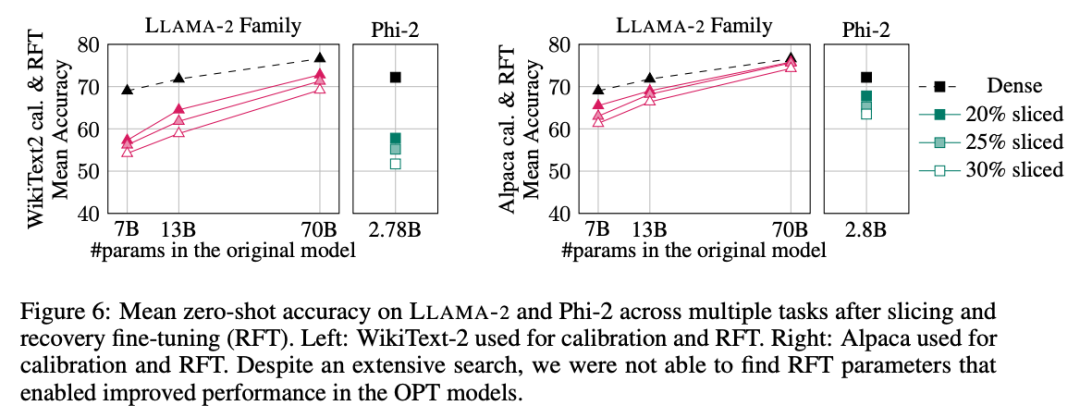
Keputusan eksperimen ditunjukkan dalam Rajah 6. Ia boleh didapati bahawa terdapat perbezaan yang ketara dalam keputusan RFT antara set data WikiText-2 dan Alpaca, dan model menunjukkan prestasi yang lebih baik dalam set data Alpaca. Penulis percaya bahawa sebab perbezaan adalah bahawa tugasan dalam set data Alpaca lebih dekat dengan tugas garis dasar.

Untuk model LLAMA-2 70B terbesar, selepas pemangkasan 30% dan melakukan RFT, ketepatan purata akhir dalam dataset Alpaca ialah 74.3%, dan ketepatan model tumpat asal ialah 76.6%. Model yang disesuaikan LLAMA-2 70B mengekalkan kira-kira 51.6B parameter dan daya pemprosesannya dipertingkatkan dengan ketara.

Pengarang juga mendapati bahawa Phi-2 tidak dapat memulihkan ketepatan asal daripada model yang dipangkas dalam set data WikiText-2, tetapi ia boleh memulihkan beberapa titik peratusan ketepatan dalam set data Alpaca. Phi-2, dipotong sebanyak 25% dan RFTed, mempunyai ketepatan purata 65.2% dalam dataset Alpaca, dan ketepatan model tumpat asal ialah 72.2%. Model yang dipangkas mengekalkan parameter 2.2B dan mengekalkan 90.3% ketepatan model 2.8B. Ini menunjukkan model bahasa kecil pun boleh dipangkas dengan berkesan. . Pendekatan ini meningkatkan kerumitan pengiraan (bilangan operasi titik terapung) model mampatan SliceGPT dan meningkatkan kecekapan pemindahan data.

Pada GPU 80GB H100, tetapkan panjang jujukan kepada 128 dan gandakan panjang jujukan untuk mencari daya pemprosesan maksimum sehingga memori GPU habis atau daya pemprosesan menurun. Pengarang membandingkan daya pengeluaran 25% dan 50% model pemangkasan kepada model padat asal pada GPU 80GB H100. Model yang dipangkas sebanyak 25% mencapai peningkatan daya pemprosesan sehingga 1.55x. Dengan 50% keratan, model terbesar mencapai peningkatan ketara dalam daya pengeluaran sebanyak 3.13x dan 1.87x menggunakan satu GPU. Ini menunjukkan bahawa apabila bilangan GPU ditetapkan, daya pemprosesan model yang dipangkas akan mencapai 6.26 kali dan 3.75 kali masing-masing daripada model tumpat asal.

Selepas 50% pemangkasan, walaupun kerumitan yang dikekalkan oleh SliceGPT dalam WikiText2 adalah lebih teruk daripada SparseGPT 2:4, daya pemprosesan jauh melebihi kaedah SparseGPT. Untuk model bersaiz 13B, daya pemprosesan juga mungkin bertambah baik untuk model yang lebih kecil pada GPU pengguna dengan memori yang kurang.

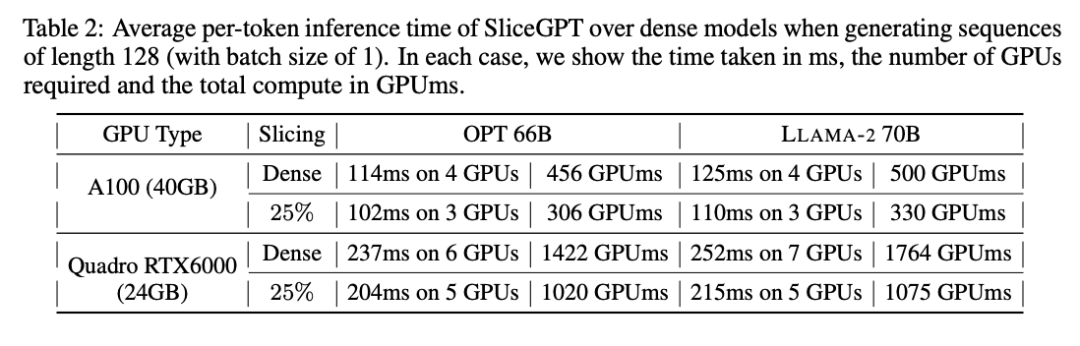
Masa inferens

Pengarang juga mengkaji masa berjalan hujung ke hujung model yang dimampatkan menggunakan SliceGPT. Jadual 2 membandingkan masa yang diperlukan untuk menjana token tunggal untuk model OPT 66B dan LLAMA-2 70B pada GPU Quadro RTX6000 dan A100. Ia boleh didapati bahawa pada GPU RTX6000, selepas memangkas model sebanyak 25%, kelajuan inferens meningkat sebanyak 16-17% pada GPU A100, kelajuan meningkat sebanyak 11-13%. Untuk LLAMA-2 70B, usaha pengiraan yang diperlukan menggunakan GPU RTX6000 dikurangkan sebanyak 64% berbanding model tumpat asal. Pengarang mengaitkan peningkatan ini kepada penggantian SliceGPT bagi matriks berat asal dengan matriks berat yang lebih kecil dan penggunaan biji padat, yang tidak boleh dicapai oleh skim pemangkasan lain.

Pengarang menyatakan bahawa pada masa penulisan, garis dasar mereka SparseGPT 2:4 tidak dapat mencapai peningkatan prestasi hujung ke hujung. Sebaliknya, mereka membandingkan SliceGPT kepada SparseGPT 2:4 dengan membandingkan masa relatif setiap operasi dalam lapisan pengubah. Mereka mendapati bahawa untuk model besar, SliceGPT (25%) bersaing dengan SparseGPT (2:4) dari segi peningkatan kelajuan dan kebingungan.

Kos Pengiraan

Semua model LLAMA-2, OPT dan Phi-2 boleh dibahagikan dalam 1 hingga 3 jam pada satu GPU. Seperti yang ditunjukkan dalam Jadual 3, dengan penalaan halus pemulihan, semua LM boleh dimampatkan dalam masa 1 hingga 5 jam.

Untuk maklumat lanjut, sila rujuk kertas asal.

Atas ialah kandungan terperinci Model besar juga boleh dihiris, dan Microsoft SliceGPT sangat meningkatkan kecekapan pengiraan LLAMA-2. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!