Mengapakah Gaussian Splatting begitu popular dalam pemanduan autonomi sehingga NeRF mula ditinggalkan?

Ditulis di hadapan & pemahaman peribadi pengarang

Percikan Gaussian tiga dimensi (3DGS) ialah teknologi revolusioner yang telah muncul dalam bidang medan sinaran eksplisit dan grafik komputer sejak beberapa tahun kebelakangan ini. Kaedah inovatif ini dicirikan oleh penggunaan berjuta-juta Gaussians 3D, yang sangat berbeza daripada kaedah medan sinaran saraf (NeRF), yang terutamanya menggunakan model berasaskan koordinat tersirat untuk memetakan koordinat spatial kepada nilai piksel. Dengan perwakilan adegan yang eksplisit dan algoritma pemaparan yang boleh dibezakan, 3D GS bukan sahaja menjamin keupayaan pemaparan masa nyata, tetapi juga memperkenalkan tahap kawalan dan pengeditan adegan yang tidak pernah berlaku sebelum ini. Ini meletakkan 3D GS sebagai penukar permainan yang berpotensi untuk pembinaan semula dan perwakilan 3D generasi akan datang. Untuk tujuan ini, kami menyediakan gambaran sistematik pertama tentang perkembangan terkini dan sumbangan utama dalam bidang 3D GS. Pertama, prinsip dan formula asas untuk kemunculan GS 3D diterokai secara terperinci, meletakkan asas untuk memahami kepentingannya. Kemudian kepraktisan 3D GS dibincangkan secara mendalam. Dengan memudahkan prestasi masa nyata, 3D GS membuka pelbagai aplikasi, daripada realiti maya kepada media interaktif dan banyak lagi. Di samping itu, analisis perbandingan model GS 3D terkemuka dijalankan dan dinilai pada pelbagai tugas penanda aras untuk menyerlahkan prestasi dan praktikalnya. Semakan ini diakhiri dengan mengenal pasti cabaran semasa dan mencadangkan jalan yang berpotensi untuk penyelidikan masa depan dalam bidang ini. Dengan tinjauan ini, kami berhasrat untuk menyediakan kedua-dua pendatang baru dan penyelidik berpengalaman dengan sumber yang berharga, merangsang penerokaan dan kemajuan selanjutnya dalam representasi medan sinaran yang boleh digunakan dan tidak jelas.

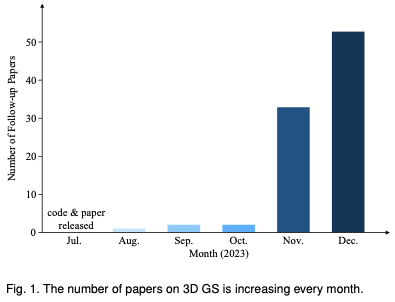
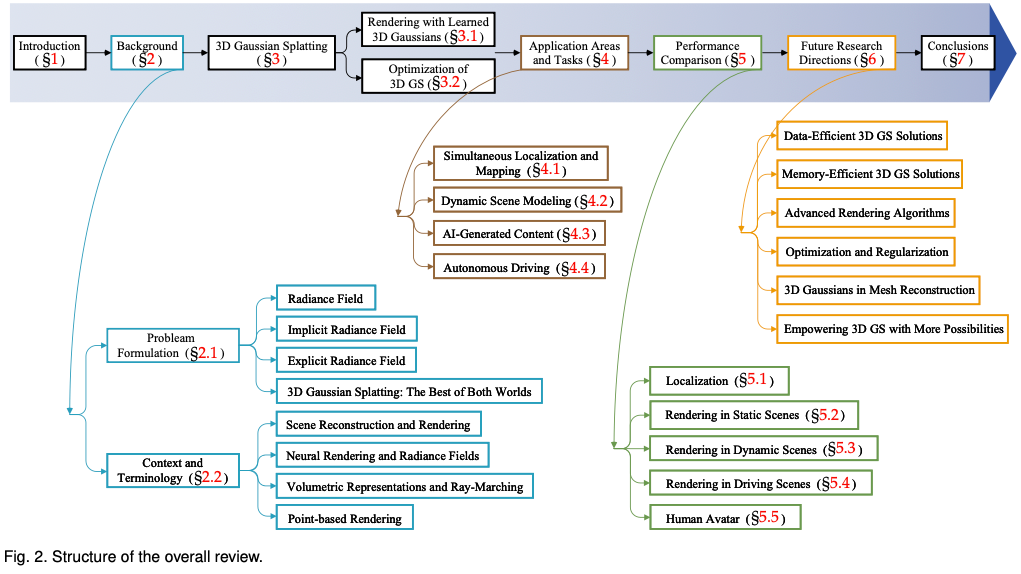
Untuk membantu pembaca mengikuti perkembangan pesat 3D GS, kami menyediakan tinjauan tinjauan pertama tentang 3D GS. Kami telah secara sistematik dan tepat pada masanya mengumpul literatur terkini yang paling penting mengenai topik ini, terutamanya daripada arxiv. Matlamat artikel ini adalah untuk menyediakan analisis yang komprehensif dan terkini tentang pembangunan awal, asas teori, dan aplikasi baru muncul 3D GS, yang menonjolkan potensi revolusionernya dalam bidang. Memandangkan sifat 3D GS yang baru lahir tetapi berkembang pesat, tinjauan ini juga bertujuan untuk mengenal pasti dan membincangkan cabaran semasa dan prospek masa depan dalam bidang ini. Kami memberikan pandangan tentang hala tuju penyelidikan yang sedang berjalan dan potensi kemajuan yang 3D GS mungkin memudahkan. Kajian semula ini diharap bukan sahaja memberi pengetahuan akademik tetapi juga merangsang penyelidikan dan inovasi seterusnya dalam bidang ini. Struktur artikel ini adalah seperti berikut: (Rajah 2) Sila ambil perhatian bahawa semua kandungan adalah berdasarkan kesusasteraan dan hasil penyelidikan terkini dan bertujuan untuk memberikan pembaca maklumat yang komprehensif dan tepat pada masanya tentang 3D GS.

Pengenalan Latar Belakang

Bahagian ini memperkenalkan formula ringkas medan sinaran, yang merupakan konsep utama dalam pemaparan pemandangan. Medan sinaran boleh diwakili oleh dua jenis utama: tersirat, seperti NeRF, yang menggunakan rangkaian saraf untuk pemaparan langsung tetapi memerlukan pengiraan dan eksplisit, seperti jejaring, yang menggunakan struktur diskret untuk akses yang lebih pantas tetapi kurang memori Penggunaan yang lebih tinggi; Seterusnya, kami akan meneroka lebih lanjut sambungan ke kawasan yang berkaitan seperti pembinaan semula pemandangan dan rendering.

Definisi Masalah

Medan Sinaran: Medan sinaran ialah perwakilan taburan cahaya dalam ruang tiga dimensi, yang merakam cara cahaya berinteraksi dengan permukaan dan bahan dalam persekitaran. Secara matematik, medan sinaran boleh digambarkan sebagai fungsi yang memetakan titik dalam ruang dan arah yang ditentukan oleh koordinat sfera kepada nilai sinaran bukan negatif. Medan sinaran boleh dirangkumkan oleh perwakilan tersirat atau eksplisit, setiap satunya mempunyai perwakilan pemandangan tertentu dan kelebihan rendering.

Medan Sinaran Tersirat: Medan sinaran tersirat mewakili taburan cahaya dalam pemandangan tanpa mentakrifkan geometri tempat kejadian secara eksplisit. Dalam era pembelajaran mendalam, ia sering menggunakan rangkaian saraf untuk mempelajari perwakilan adegan volumetrik berterusan. Contoh yang paling menonjol ialah NeRF. Dalam NeRF, rangkaian MLP digunakan untuk memetakan satu set koordinat spatial dan melihat arah kepada warna dan nilai ketumpatan. Sinaran mana-mana titik tidak disimpan secara eksplisit tetapi dikira dalam masa nyata dengan menanyakan rangkaian saraf. Oleh itu, fungsi boleh ditulis sebagai:

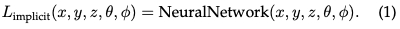
Format ini membenarkan perwakilan padat dan boleh dibezakan bagi pemandangan kompleks, walaupun dengan beban pengiraan yang lebih tinggi semasa pemaparan disebabkan oleh perjalanan sinar volumetrik.

Medan sinaran eksplisit: Sebaliknya, medan sinaran eksplisit secara langsung mewakili taburan cahaya dalam struktur spatial diskret, seperti grid voxel atau set titik. Setiap elemen dalam struktur menyimpan maklumat sinaran untuk kedudukannya yang sepadan dalam ruang. Pendekatan ini membolehkan akses yang lebih langsung dan selalunya lebih pantas kepada data radiometrik, tetapi pada kos penggunaan memori yang lebih tinggi dan kemungkinan resolusi yang lebih rendah. Bentuk umum perwakilan medan sinaran eksplisit boleh ditulis sebagai:

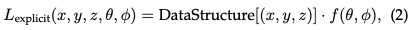
Di mana DataStructure boleh menjadi grid atau awan titik, iaitu fungsi yang mengubah suai sinaran berdasarkan arah tontonan.

Yang terbaik dari kedua-dua dunia 3D Gaussian Splatting: 3D GS mewakili peralihan daripada medan sinaran tersirat kepada eksplisit. Ia mengeksploitasi kelebihan kedua-dua kaedah dengan memanfaatkan Gaussians 3D sebagai perwakilan yang fleksibel dan cekap. Pekali Gaussian ini dioptimumkan untuk mewakili pemandangan dengan tepat, menggabungkan kelebihan pengoptimuman berasaskan rangkaian saraf dan penyimpanan data berstruktur eksplisit. Pendekatan hibrid ini bertujuan untuk mencapai pemaparan berkualiti tinggi dengan latihan yang lebih pantas dan prestasi masa nyata, terutamanya untuk adegan yang kompleks dan output resolusi tinggi. Perwakilan Gaussian 3D dirumuskan sebagai:

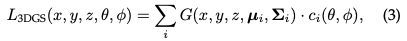
Konteks dan Terminologi

Banyak teknologi dan disiplin penyelidikan berkait rapat dengan 3D GS, yang akan diterangkan secara ringkas di bawah.

Pembinaan Semula Adegan dan Perenderan: Secara kasarnya, pembinaan semula pemandangan melibatkan penciptaan model 3D pemandangan daripada koleksi imej atau data lain. Rendering ialah istilah yang lebih khusus yang memfokuskan pada menukar maklumat yang boleh dibaca komputer (contohnya, objek 3D dalam pemandangan) kepada imej berasaskan piksel. Teknik awal adalah berdasarkan medan cahaya untuk menghasilkan imej yang realistik. Algoritma Structure-from-motion (SfM) dan stereo multi-view (MVS) memajukan lagi medan dengan menganggar struktur 3D daripada jujukan imej. Kaedah sejarah ini meletakkan asas untuk pembinaan semula adegan dan teknik rendering yang lebih kompleks.

Rendering Neural dengan Medan Radiant: Rendering Neural menggabungkan pembelajaran mendalam dengan teknik grafik tradisional untuk mencipta imej fotorealistik. Percubaan awal menggunakan rangkaian saraf konvolusi (CNN) untuk menganggarkan pemberat hibrid atau penyelesaian ruang tekstur. Medan sinaran mewakili fungsi yang menerangkan jumlah cahaya yang bergerak dalam setiap arah melalui setiap titik dalam ruang. NeRF menggunakan rangkaian saraf untuk memodelkan medan sinaran, membolehkan pemaparan pemandangan yang terperinci dan realistik.

Perwakilan Jilid dan Ray-Marching: Perwakilan volum memodelkan objek dan pemandangan bukan sahaja sebagai permukaan, tetapi juga sebagai jilid yang diisi dengan bahan atau ruang kosong. Kaedah ini membolehkan pemaparan fenomena yang lebih tepat seperti kabus, asap atau bahan lut sinar. Ray-Marching ialah teknik yang digunakan dengan perwakilan isipadu untuk memaparkan imej dengan menjejaki laluan cahaya melalui volum secara berperingkat. NeRF berkongsi semangat yang sama dalam perarakan sinar volumetrik dan memperkenalkan pensampelan kepentingan dan pengekodan kedudukan untuk meningkatkan kualiti imej yang disintesis. Semasa memberikan hasil yang berkualiti tinggi, perjalanan sinar volum adalah mahal dari segi pengiraan, mendorong carian untuk kaedah yang lebih cekap seperti 3D GS.

Perenderan Berasaskan Titik: Perenderan berasaskan titik ialah teknik untuk menggambarkan pemandangan 3D menggunakan titik dan bukannya poligon tradisional. Pendekatan ini amat berkesan untuk menghasilkan data geometri yang kompleks, tidak berstruktur atau jarang. Mata boleh dipertingkatkan dengan sifat tambahan, seperti deskriptor saraf yang boleh dipelajari, dan diberikan dengan cekap, tetapi pendekatan ini mungkin mengalami masalah seperti lubang dalam rendering atau kesan aliasing. GS 3D memanjangkan konsep ini dengan menggunakan Gaussians anisotropik untuk mencapai perwakilan adegan yang lebih berterusan dan padat.

Gaussian 3D untuk Medan Sinaran Eksplisit

3D GS ialah satu kejayaan dalam pemaparan imej masa nyata, resolusi tinggi tanpa bergantung pada komponen saraf.

Belajar Gaussians 3D untuk sintesis perspektif baharu

Pertimbangkan pemandangan yang diwakili oleh (berjuta-juta) Gaussians 3D yang dioptimumkan. Matlamatnya adalah untuk menjana imej berdasarkan pose kamera yang ditentukan. Ingat bahawa NeRF melaksanakan tugas ini dengan menuntut perjalanan sinar volumetrik secara pengiraan, mensampel titik ruang 3D untuk setiap piksel. Mod ini menyukarkan untuk mencapai sintesis imej resolusi tinggi dan tidak dapat mencapai kelajuan pemaparan masa nyata. Sebaliknya, 3D GS mula-mula menayangkan Gaussian 3D ini pada satah imej berasaskan piksel, satu proses yang dipanggil "percikan" (Rajah 3a). 3D GS kemudian mengisih Gaussian ini dan mengira nilai setiap piksel. Seperti yang ditunjukkan dalam rajah, pemaparan NeRF dan 3D GS boleh dilihat sebagai proses songsang antara satu sama lain. Dalam perkara berikut, kita mulakan dengan definisi Gaussian 3D, yang merupakan elemen terkecil perwakilan pemandangan dalam GS 3D. Seterusnya kami menerangkan cara menggunakan Gaussians 3D ini untuk pemaparan yang boleh dibezakan. Akhirnya, teknologi pecutan yang digunakan dalam 3D GS diperkenalkan, yang merupakan kunci kepada pemaparan pantas.

Sifat Gaussian tiga dimensi: Ciri Gaussian tiga dimensi ialah pusat (kedudukan) μ, kelegapan α, matriks kovarian tiga dimensi ∑ dan warna c. Untuk penampilan bergantung pada pandangan, c diwakili oleh harmonik sfera. Semua atribut boleh dipelajari dan dioptimumkan melalui perambatan belakang.

Frustum Culling: Memandangkan pose kamera yang ditentukan, langkah ini menentukan Gaussians 3D yang terletak di luar frustum kamera. Dengan melakukan ini, Gaussians 3D di luar paparan yang diberikan tidak akan terlibat dalam pengiraan seterusnya, sekali gus menjimatkan sumber pengiraan.

Percikan: ** Dalam langkah ini, Gaussian 3D (elipsoid) ditayangkan ke dalam ruang imej 2D (elipsoid) untuk pemaparan. Memandangkan penjelmaan paparan W dan matriks kovarians 3D Σ, matriks kovarians 2D yang diunjurkan Σ′ dikira menggunakan formula berikut:

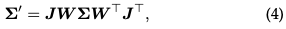
di mana J ialah matriks Jacobian bagi penghampiran affine bagi transformasi unjuran.

Perenderan Pixel: Sebelum kita menyelami versi akhir 3D GS, kami mula-mula memperincikan bentuknya yang lebih ringkas untuk mendapatkan pemahaman yang lebih mendalam tentang cara ia berfungsi. 3D GS menggunakan pelbagai teknologi untuk memudahkan pengkomputeran selari. Diberi kedudukan piksel Sintesis alfa kemudiannya digunakan untuk mengira warna akhir untuk piksel tersebut:

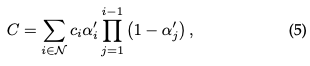
di manakah warna yang dipelajari dan kelegapan akhir ialah hasil daripada kelegapan yang dipelajari dan nilai Gaussian:

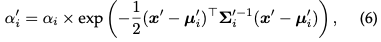
di mana x′ dan μ ialah koordinat dalam ruang unjuran. Memandangkan menjana senarai diisih yang diperlukan sukar untuk disejajarkan, proses pemaparan yang diterangkan mungkin lebih perlahan berbanding dengan NeRF, yang merupakan kebimbangan yang sah. Malah, kebimbangan ini adalah sah; kelajuan pemaparan boleh terjejas dengan ketara apabila menggunakan pendekatan piksel demi piksel yang mudah ini. Untuk mencapai pemaparan masa nyata, 3DGS membuat beberapa konsesi untuk menampung pengkomputeran selari.

Jubin (Tampalan): Untuk mengelakkan kos pengiraan memperoleh pekali Gaussian bagi setiap piksel, 3D GS memindahkan ketepatan dari aras piksel ke butiran tahap tampalan. Khususnya, 3D GS pada mulanya membahagikan imej kepada berbilang blok tidak bertindih, dipanggil "jubin" dalam kertas asal. Rajah 3b menyediakan ilustrasi jubin. Setiap jubin terdiri daripada 16×16 piksel. GS 3D selanjutnya menentukan jubin yang bersilang dengan peta Gaussian yang diunjurkan ini. Dengan mengandaikan bahawa Gaussian yang diunjurkan mungkin meliputi berbilang jubin, pendekatan logiknya terdiri daripada menyalin Gaussian, memberikan setiap salinan pengecam jubin yang berkaitan (iaitu, ID jubin).

Perenderan selari: Selepas menyalin, 3D GS menggabungkan ID jubin individu dengan nilai kedalaman yang diperoleh daripada transformasi pandangan setiap Gaussian. Ini menghasilkan senarai bait yang tidak diisih, di mana bit tertib tinggi mewakili ID jubin dan bit tertib rendah mewakili kedalaman. Dengan melakukan ini, senarai yang diisih boleh digunakan secara langsung untuk pemaparan (iaitu penggubahan alfa). Rajah 3c dan 3d menyediakan demonstrasi visual konsep ini. Perlu ditekankan bahawa pemaparan setiap jubin dan piksel berlaku secara berasingan, menjadikan proses ini sesuai untuk pengkomputeran selari. Faedah lain ialah setiap piksel jubin mempunyai akses kepada memori dikongsi bersama dan mengekalkan jujukan bacaan yang seragam, membolehkan penggbahan alfa dilakukan secara selari dengan kecekapan yang lebih tinggi. Dalam pelaksanaan rasmi kertas asal, rangka kerja memperlakukan pemprosesan jubin dan piksel masing-masing sebagai serupa dengan blok dan benang dalam seni bina pengaturcaraan CUDA.

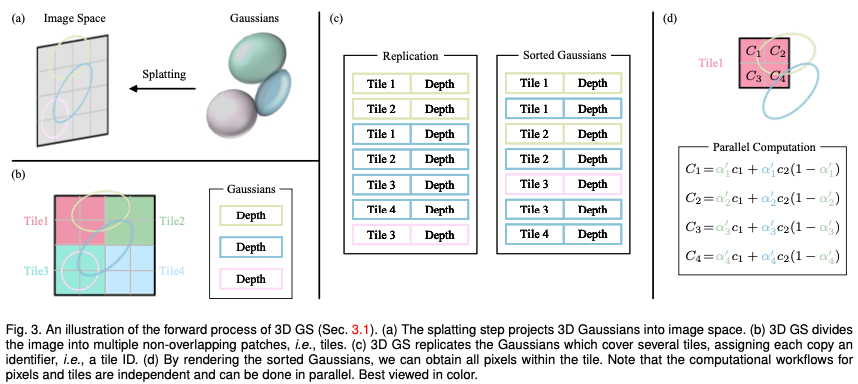
Ringkasnya, 3D GS memperkenalkan beberapa anggaran dalam peringkat pemprosesan hadapan untuk meningkatkan kecekapan pengiraan sambil mengekalkan standard kualiti sintesis imej yang tinggi. . Di satu pihak, sifat Gaussians 3D harus dioptimumkan melalui pemaparan yang boleh dibezakan untuk menyesuaikan diri dengan tekstur adegan tertentu. Sebaliknya, bilangan Gaussians 3D yang boleh mewakili pemandangan tertentu dengan baik tidak diketahui terlebih dahulu. Satu pendekatan yang menjanjikan adalah untuk mempunyai rangkaian saraf secara automatik mempelajari ketumpatan Gaussian 3D. Kami akan membincangkan cara mengoptimumkan sifat setiap Gaussian dan cara mengawal ketumpatan Gaussian. Kedua-dua proses ini dijalin dalam aliran kerja pengoptimuman. Memandangkan terdapat banyak hiperparameter yang ditetapkan secara manual semasa pengoptimuman, kami meninggalkan simbol kebanyakan hiperparameter demi kejelasan.

Pengoptimuman parameter

Fungsi kehilangan:

Setelah sintesis imej selesai, kerugian dikira sebagai perbezaan antara imej yang diberikan dan GT:

ialah fungsi 3D-GS ialah sedikit berbeza daripada NeRFs . Disebabkan kawad sinar yang memakan masa, NeRF biasanya dikira pada tahap piksel dan bukannya tahap imej.

Kemas kini parameter: 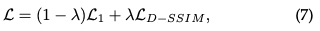Kebanyakan sifat Gaussian 3D boleh dioptimumkan terus melalui perambatan belakang. Perlu diingatkan bahawa mengoptimumkan secara langsung matriks kovarians Σ membawa kepada matriks semidefinite bukan positif, yang tidak mematuhi tafsiran fizikal yang biasanya dikaitkan dengan matriks kovarians. Untuk mengelakkan masalah ini, 3D GS memilih untuk mengoptimumkan kuaternion q dan vektor 3D s. q dan s masing-masing mewakili putaran dan skala. Pendekatan ini membolehkan matriks kovarians ∑ dibina semula seperti berikut:

Kawalan Ketumpatan

Permulaan: 3D GS bermula dari set awal SfM atau titik jarang yang dimulakan secara rawak. Kemudian, ketumpatan titik dan pemangkasan digunakan untuk mengawal ketumpatan Gaussian tiga dimensi.

Pempadatan titik: Dalam peringkat penumpuan titik, 3D GS secara adaptif meningkatkan ketumpatan Gaussian untuk menangkap butiran pemandangan dengan lebih baik. Proses ini memberi perhatian khusus kepada kawasan yang tiada ciri geometri atau taburan Gaussian terlalu berselerak. Pemadatan dilakukan selepas bilangan lelaran tertentu, menyasarkan Gaussian yang mempamerkan kecerunan kedudukan ruang pandangan yang besar (iaitu, di atas ambang tertentu). Ia melibatkan pengklonan Gaussian kecil di kawasan yang kurang dibina semula, atau membelah Gaussian besar di kawasan yang terlalu dibina semula. Untuk pengklonan, salinan Gaussian dibuat dan dialihkan ke arah kecerunan kedudukan. Untuk membelah, dua Gaussian yang lebih kecil menggantikan satu Gaussian yang lebih besar, mengurangkan saiznya dengan faktor tertentu. Langkah ini mencari pengedaran dan perwakilan Gaussian yang optimum dalam ruang 3D, sekali gus meningkatkan kualiti keseluruhan pembinaan semula.

Pencantas mata: Peringkat pemangkasan titik melibatkan penyingkiran Gaussian yang berlebihan atau kurang berpengaruh, yang boleh dianggap sebagai proses penyelarasan sedikit sebanyak. Langkah ini dilakukan dengan menghapuskan Gaussian yang hampir lutsinar (α di bawah ambang tertentu) dan Gaussian yang terlalu besar dalam ruang dunia atau ruang paparan. Tambahan pula, untuk mengelakkan peningkatan tidak munasabah dalam ketumpatan Gaussians berhampiran kamera input, nilai alfa Gaussians ditetapkan hampir kepada sifar selepas bilangan lelaran tertentu. Ini membolehkan mengawal peningkatan yang diperlukan dalam ketumpatan Gaussians sambil menghapuskan Gaussian yang berlebihan. Proses ini bukan sahaja membantu menjimatkan sumber pengiraan tetapi juga memastikan bahawa perwakilan pemandangan oleh Gaussians dalam model kekal tepat dan cekap.

Bidang dan tugasan aplikasi

Potensi transformatif GS 3D menjangkau jauh melebihi kemajuan teori dan pengiraannya. Bahagian ini menyelidiki pelbagai bidang aplikasi perintis di mana GS 3D mempunyai kesan yang ketara, seperti robotik, pembinaan semula dan perwakilan pemandangan, kandungan yang dijana AI, pemanduan autonomi dan juga disiplin saintifik yang lain. Aplikasi 3D GS menunjukkan kepelbagaian dan potensi revolusionernya. Di sini, kami menggariskan beberapa kawasan aplikasi yang paling ketara, memberikan pandangan tentang cara 3D GS membentuk sempadan baharu di setiap kawasan.

SLAM

SLAM ialah masalah pengiraan teras untuk sistem robotik dan autonomi. Ia melibatkan cabaran robot atau peranti memahami kedudukannya dalam persekitaran yang tidak diketahui sambil memetakan susun atur persekitaran. SLAM adalah kritikal dalam pelbagai aplikasi, termasuk kereta pandu sendiri, realiti tambahan dan navigasi robot. Teras SLAM adalah untuk mencipta peta persekitaran yang tidak diketahui dan menentukan lokasi peranti pada peta dalam masa nyata. Oleh itu, SLAM menimbulkan cabaran besar kepada teknologi perwakilan pemandangan intensif pengiraan dan juga merupakan tempat ujian yang baik untuk GS 3D.

3D GS memasuki bidang SLAM sebagai kaedah perwakilan adegan yang inovatif. Sistem SLAM tradisional biasanya menggunakan awan titik/permukaan atau jerat voxel untuk mewakili persekitaran. Sebaliknya, GS 3D menggunakan Gaussians anisotropik untuk mewakili alam sekitar dengan lebih baik. Perwakilan ini memberikan beberapa faedah: 1) Kecekapan: Kawal ketumpatan Gaussians 3D secara adaptif untuk mewakili data spatial secara padat dan mengurangkan beban pengiraan. 2) Ketepatan: Anisotropik Gaussian membolehkan pemodelan persekitaran yang lebih terperinci dan tepat, terutamanya sesuai untuk adegan yang kompleks atau berubah secara dinamik. 3) Kebolehsuaian: GS 3D boleh menyesuaikan diri dengan pelbagai skala dan persekitaran yang kompleks, menjadikannya sesuai untuk aplikasi SLAM yang berbeza. Beberapa kajian inovatif telah menggunakan percikan Gaussian 3D dalam SLAM, menunjukkan potensi dan serba boleh paradigma ini.

Pemodelan Adegan Dinamik

Pemodelan adegan dinamik merujuk kepada proses menangkap dan mewakili struktur tiga dimensi dan rupa adegan yang berubah mengikut masa. Ini melibatkan penciptaan model digital yang menggambarkan geometri, gerakan dan aspek visual objek dalam pemandangan dengan tepat. Pemodelan pemandangan dinamik adalah penting dalam pelbagai aplikasi, termasuk realiti maya dan tambahan, animasi 3D dan penglihatan komputer. 4D Gaussian Scattering (4D GS) memanjangkan konsep 3D GS kepada adegan dinamik. Ia menggabungkan dimensi temporal, membenarkan perwakilan dan pemaparan adegan yang berubah dari semasa ke semasa. Paradigma ini memberikan peningkatan yang ketara dalam menghasilkan pemandangan dinamik dalam masa nyata sambil mengekalkan output visual berkualiti tinggi.

AIGC

AIGC merujuk kepada kandungan digital yang dicipta secara autonomi atau diubah dengan ketara oleh sistem kecerdasan buatan, terutamanya dalam bidang penglihatan komputer, pemprosesan bahasa semula jadi dan pembelajaran mesin. AIGC dicirikan oleh keupayaannya untuk mensimulasikan, melanjutkan atau meningkatkan kandungan yang dijana secara buatan, membolehkan aplikasi daripada sintesis imej fotorealistik kepada penciptaan naratif dinamik. Kepentingan AIGC terletak pada potensi transformatifnya dalam pelbagai bidang, termasuk hiburan, pendidikan dan pembangunan teknologi. Ia merupakan elemen utama dalam landskap penciptaan kandungan digital yang sedang berkembang, menyediakan alternatif berskala, boleh disesuaikan dan selalunya lebih cekap kepada kaedah tradisional.

Ciri 3D GS yang tidak jelas ini memudahkan keupayaan pemaparan masa nyata dan tahap kawalan dan penyuntingan yang belum pernah berlaku sebelum ini, menjadikannya sangat relevan untuk aplikasi AIGC. Perwakilan adegan eksplisit 3D GS dan algoritma pemaparan boleh dibezakan memenuhi sepenuhnya keperluan AIGC untuk menjana kandungan kesetiaan tinggi, masa nyata dan boleh diedit, yang penting untuk aplikasi dalam realiti maya, media interaktif dan bidang lain.

Pemandu Autonomi

Pemandu Autonomi direka untuk membolehkan kenderaan mengemudi dan beroperasi tanpa campur tangan manusia. Kenderaan ini dilengkapi dengan set penderia, termasuk kamera, LiDAR dan radar, digabungkan dengan algoritma lanjutan, model pembelajaran mesin dan kuasa pengkomputeran yang berkuasa. Matlamat utama adalah untuk merasakan persekitaran, membuat keputusan termaklum, dan melaksanakan manuver dengan selamat dan cekap. Pemanduan autonomi berpotensi untuk mengubah pengangkutan, memberikan faedah utama seperti meningkatkan keselamatan jalan raya dengan mengurangkan kesilapan manusia, meningkatkan mobiliti bagi mereka yang tidak dapat memandu, dan mengoptimumkan aliran trafik, sekali gus mengurangkan kesesakan dan kesan alam sekitar.

Kenderaan autonomi perlu merasakan dan mentafsir persekitaran sekeliling untuk memandu dengan selamat. Ini termasuk membina semula adegan pemanduan dalam masa nyata, mengenal pasti objek statik dan dinamik dengan tepat, dan memahami hubungan ruang dan pergerakannya. Dalam senario pemanduan dinamik, persekitaran sentiasa berubah disebabkan oleh objek yang bergerak seperti kenderaan lain, pejalan kaki atau haiwan. Membina semula adegan ini dengan tepat dalam masa nyata adalah penting untuk navigasi yang selamat, tetapi merupakan satu cabaran kerana kerumitan dan kebolehubahan elemen yang terlibat. Dalam pemanduan autonomi, GS 3D boleh digunakan untuk membina semula pemandangan dengan menggabungkan titik data, seperti yang diperoleh daripada penderia seperti LiDAR, ke dalam perwakilan yang padu dan berterusan. Ini amat berguna untuk mengendalikan ketumpatan titik data yang berbeza dan memastikan pembinaan semula latar belakang statik dan objek dinamik yang lancar dan tepat dalam adegan. Setakat ini, terdapat beberapa karya yang menggunakan Gaussian 3D untuk memodelkan pemandangan pemanduan/jalanan dinamik dan menunjukkan prestasi cemerlang dalam pembinaan semula pemandangan berbanding kaedah sedia ada.

Perbandingan Prestasi

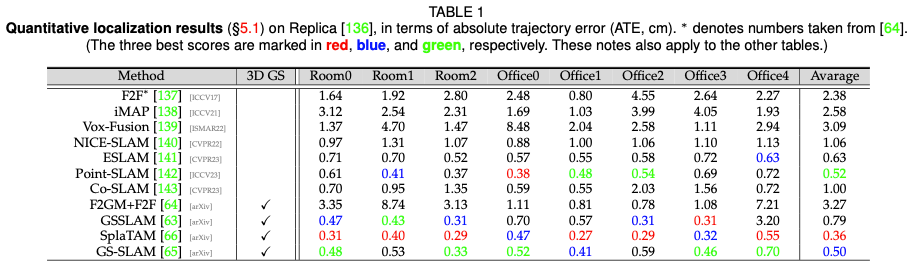
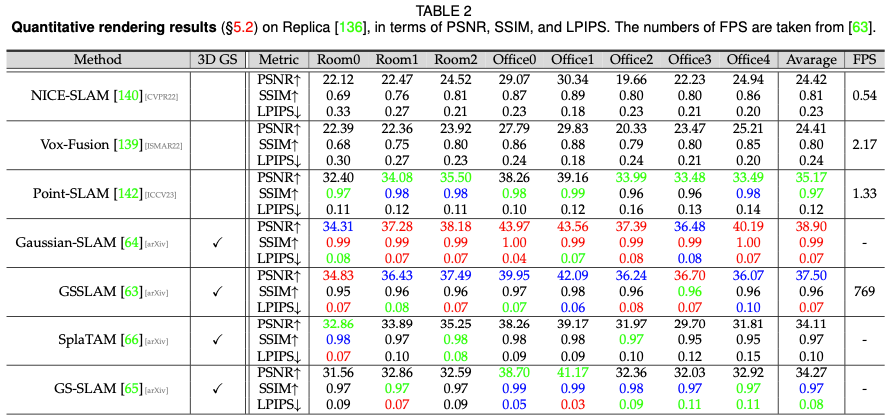
Bahagian ini menyediakan lebih banyak bukti empirikal dengan menunjukkan prestasi beberapa algoritma GS 3D yang kami bincangkan sebelum ini. Aplikasi 3D GS yang pelbagai dalam banyak tugas, ditambah dengan reka bentuk algoritma tersuai untuk setiap tugas, menjadikan perbandingan seragam semua algoritma 3D GS dalam satu tugasan atau set data tidak praktikal. Oleh itu, kami memilih tiga tugas perwakilan dalam medan GS 3D untuk penilaian prestasi yang mendalam. Persembahan diperoleh terutamanya daripada kertas asal melainkan dinyatakan sebaliknya. Prestasi pemaparan kedudukan prestasi rendering

Prestasi Manusia Digital

Arah Penyelidikan Masa Depan

Walaupun kerja susulan pada 3D GS telah mencapai kemajuan yang ketara dalam beberapa bulan kebelakangan ini, kami percaya bahawa masih terdapat beberapa cabaran yang perlu diatasi.

• Penyelesaian GS 3D yang cekap data: Menjana paparan baharu dan membina semula adegan daripada titik data terhad amat menarik, terutamanya kerana ia berpotensi untuk meningkatkan realisme dan pengalaman pengguna dengan input yang minimum. Kemajuan terkini telah meneroka penggunaan maklumat mendalam, taburan kebarangkalian padat dan pemetaan piksel-ke-Gaussian untuk memudahkan keupayaan ini. Walau bagaimanapun, penerokaan lanjut di kawasan ini masih diperlukan segera. Di samping itu, masalah ketara GS 3D ialah kejadian artifak di kawasan yang mempunyai data pemerhatian yang tidak mencukupi. Cabaran ini adalah had biasa dalam pemaparan medan sinaran, kerana data yang jarang sering membawa kepada pembinaan semula yang tidak tepat. Oleh itu, membangunkan kaedah interpolasi atau penyepaduan data baharu di kawasan yang jarang ini merupakan jalan yang menjanjikan untuk penyelidikan masa hadapan.
• Penyelesaian 3D GS yang cekap memori: Walaupun GS 3D menunjukkan keupayaan luar biasa, kebolehskalaannya menimbulkan cabaran yang ketara, terutamanya apabila digabungkan dengan pendekatan berasaskan NeRF. Yang terakhir mendapat manfaat daripada kesederhanaan menyimpan hanya parameter MLP yang dipelajari. Masalah kebolehskalaan ini menjadi semakin teruk dalam konteks pengurusan pemandangan berskala besar, di mana keperluan pengiraan dan memori meningkat dengan ketara. Oleh itu, terdapat keperluan mendesak untuk mengoptimumkan penggunaan memori semasa fasa latihan dan penyimpanan model. Meneroka struktur data yang lebih cekap dan menyiasat teknik pemampatan lanjutan merupakan jalan yang menjanjikan untuk menangani batasan ini.
• Algoritma pemaparan lanjutan: Saluran paip pemaparan semasa 3D GS adalah berpandangan ke hadapan dan boleh dioptimumkan lagi. Sebagai contoh, algoritma keterlihatan mudah boleh menyebabkan penukaran drastik tertib kedalaman/campuran Gaussian. Ini menyerlahkan peluang penting untuk penyelidikan masa depan: melaksanakan algoritma pemaparan yang lebih maju. Kaedah yang dipertingkatkan ini harus bertujuan untuk mensimulasikan dengan lebih tepat interaksi kompleks sifat cahaya dan bahan dalam adegan tertentu. Pendekatan yang menjanjikan mungkin melibatkan mengasimilasikan dan menyesuaikan prinsip yang telah ditetapkan daripada grafik komputer tradisional kepada konteks khusus GS 3D. Yang ketara dalam hal ini ialah usaha berterusan untuk menyepadukan teknik pemaparan yang dipertingkatkan atau model hibrid ke dalam rangka kerja pengiraan semasa GS 3D. Di samping itu, penerokaan rendering songsang dan aplikasinya menyediakan tanah yang subur untuk penyelidikan.
• Pengoptimuman dan penyelarasan: Walaupun Gaussian anisotropik berguna untuk mewakili geometri kompleks, ia boleh menghasilkan artifak visual. Contohnya, Gaussian 3D yang besar itu, terutamanya di kawasan yang mempunyai penampilan bergantung pada paparan, boleh menyebabkan artifak pop-in, di mana unsur-unsur visual tiba-tiba muncul atau hilang, memecahkan rendaman. Terdapat potensi penerokaan yang besar dalam penyelarasan dan pengoptimuman GS 3D. Memperkenalkan anti-aliasing boleh mengurangkan perubahan mendadak dalam kedalaman Gaussian dan susunan campuran. Penambahbaikan kepada algoritma pengoptimuman mungkin memberikan kawalan yang lebih baik ke atas pekali Gaussian dalam ruang. Selain itu, menggabungkan penyelarasan ke dalam proses pengoptimuman boleh mempercepatkan penumpuan, bunyi visual yang lancar atau meningkatkan kualiti imej. Tambahan pula, bilangan hiperparameter yang begitu besar mempengaruhi generalisasi 3D GS, yang memerlukan penyelesaian segera.
• Gaussians 3D dalam pembinaan semula jaringan: Potensi GS 3D dalam pembinaan semula jaringan dan tempatnya dalam spektrum volum dan perwakilan permukaan masih belum diterokai sepenuhnya. Terdapat keperluan mendesak untuk mengkaji bagaimana primitif Gaussian sesuai untuk tugas pembinaan semula jaringan. Penerokaan ini boleh merapatkan jurang antara pemaparan volumetrik dan kaedah berasaskan permukaan tradisional, memberikan cerapan tentang teknik dan aplikasi pemaparan baharu.
• Memperkasakan 3D GS dengan lebih banyak kemungkinan: Walaupun potensi besar 3D GS, rangkaian penuh aplikasi 3D GS masih belum diterokai. Satu jalan yang menjanjikan untuk diterokai ialah mempertingkatkan Gaussian 3D dengan sifat tambahan, seperti sifat linguistik dan fizikal yang disesuaikan untuk aplikasi tertentu. Tambahan pula, penyelidikan baru-baru ini telah mula mendedahkan keupayaan GS 3D dalam beberapa bidang, seperti anggaran pose kamera, tangkapan interaksi objek tangan dan kuantifikasi ketidakpastian. Penemuan awal ini memberikan peluang penting kepada sarjana antara disiplin untuk meneroka lebih lanjut GS 3D.

Kesimpulan

Untuk pengetahuan kami, ulasan ini memberikan gambaran menyeluruh pertama 3D GS, medan sinaran eksplisit revolusioner dan teknologi grafik komputer. Ia menggambarkan anjakan paradigma daripada kaedah NeRF tradisional, menonjolkan kelebihan 3D GS dalam pemaparan masa nyata dan kebolehkawalan yang dipertingkatkan. Analisis terperinci kami menunjukkan kelebihan 3D GS dalam aplikasi dunia sebenar, terutamanya yang memerlukan prestasi masa nyata. Kami memberikan pandangan tentang hala tuju penyelidikan masa depan dan cabaran yang tidak dapat diselesaikan dalam lapangan. Secara keseluruhannya, 3D GS ialah teknologi transformatif yang dijangka memberi impak yang besar kepada pembangunan masa depan pembinaan semula dan perwakilan 3D. Tinjauan ini bertujuan untuk berfungsi sebagai sumber asas untuk memacu penerokaan dan kemajuan selanjutnya dalam bidang yang pesat membangun ini.

Pautan asal: https://mp.weixin.qq.com/s/jH4g4Cx87nPUYN8iKaKcBA

Atas ialah kandungan terperinci Mengapakah Gaussian Splatting begitu popular dalam pemanduan autonomi sehingga NeRF mula ditinggalkan?. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!