Rumah >Peranti teknologi >AI >Meningkatkan keupayaan pengesanan dengan cekap: menembusi pengesanan sasaran kecil melebihi 200 meter
Meningkatkan keupayaan pengesanan dengan cekap: menembusi pengesanan sasaran kecil melebihi 200 meter
- PHPzke hadapan
- 2024-01-15 19:51:291119semak imbas
Artikel ini dicetak semula dengan kebenaran akaun awam Autonomous Driving Heart Sila hubungi sumber untuk mencetak semula.
Pengesanan Objek 3D berdasarkan awan titik LiDAR sentiasa menjadi masalah yang sangat klasik, kedua-dua ahli akademik dan industri telah mencadangkan pelbagai model untuk meningkatkan ketepatan, kelajuan dan keteguhan. Walau bagaimanapun, disebabkan persekitaran luar yang kompleks, prestasi Pengesanan Objek untuk awan titik luar tidak begitu baik. Awan titik LiDAR bersifat jarang Bagaimana untuk menyelesaikan masalah ini dengan cara yang disasarkan? Kertas itu memberikan jawapannya sendiri: mengekstrak maklumat berdasarkan pengagregatan maklumat siri masa. 1. Maklumat kertas Ini penting untuk kebolehpercayaan dan keselamatan kenderaan autonomi. Khususnya, kenderaan autonomi perlu dapat mengenali objek sekeliling, seperti kenderaan dan pejalan kaki, dan menentukan lokasi, saiz dan orientasinya dengan tepat. Biasanya, orang menggunakan rangkaian saraf dalam untuk memproses data LiDAR untuk menyelesaikan tugas ini.
Kebanyakan literatur sedia ada memfokuskan pada kaedah bingkai tunggal, iaitu menggunakan data yang diimbas oleh satu sensor pada satu masa. Pendekatan ini berprestasi baik pada penanda aras klasik dengan objek pada jarak sehingga 75 meter. Walau bagaimanapun, awan titik lidar sememangnya jarang, terutamanya pada julat yang jauh. Oleh itu, kertas itu menyatakan bahawa menggunakan hanya satu imbasan untuk pengesanan jarak jauh (cth., sehingga 200 meter) tidak mencukupi. Ini bermakna kaedah gabungan berbilang bingkai diperlukan untuk meningkatkan ketumpatan awan titik dan meningkatkan ketepatan pengukuran jarak. Dengan mendaftar dan menggabungkan data imbasan daripada beberapa langkah masa, pembinaan semula pemandangan dan hasil pengukuran jarak yang lebih lengkap dan tepat boleh diperolehi. Kaedah sedemikian mempunyai kebolehpercayaan dan keteguhan yang lebih tinggi dalam tugas seperti pengesanan sasaran jarak jauh dan mengelakkan halangan. Oleh itu, sumbangan kertas kerja adalah untuk mencadangkan kaedah berdasarkan gabungan pelbagai bingkaiUntuk menyelesaikan masalah ini, satu kaedah adalah dengan terus memperoleh data imbasan lidar melalui pengagregatan awan titik untuk mendapatkan input yang lebih padat. Walau bagaimanapun, pendekatan ini adalah mahal dari segi pengiraan dan gagal memanfaatkan sepenuhnya pengagregatan dalam rangkaian. Oleh itu, alternatif yang jelas adalah dengan menggunakan pendekatan rekursif untuk menyelesaikan masalah ini dengan mengumpul maklumat secara beransur-ansur. Kaedah rekursif sentiasa mengemas kini maklumat dari semasa ke semasa, memberikan hasil yang lebih tepat dan komprehensif. Dengan kaedah rekursif, sejumlah besar data input boleh diproses dengan cekap dan lebih cekap dari segi pengiraan. Dengan cara ini, kita boleh menjimatkan sumber pengkomputeran semasa menyelesaikan masalah.
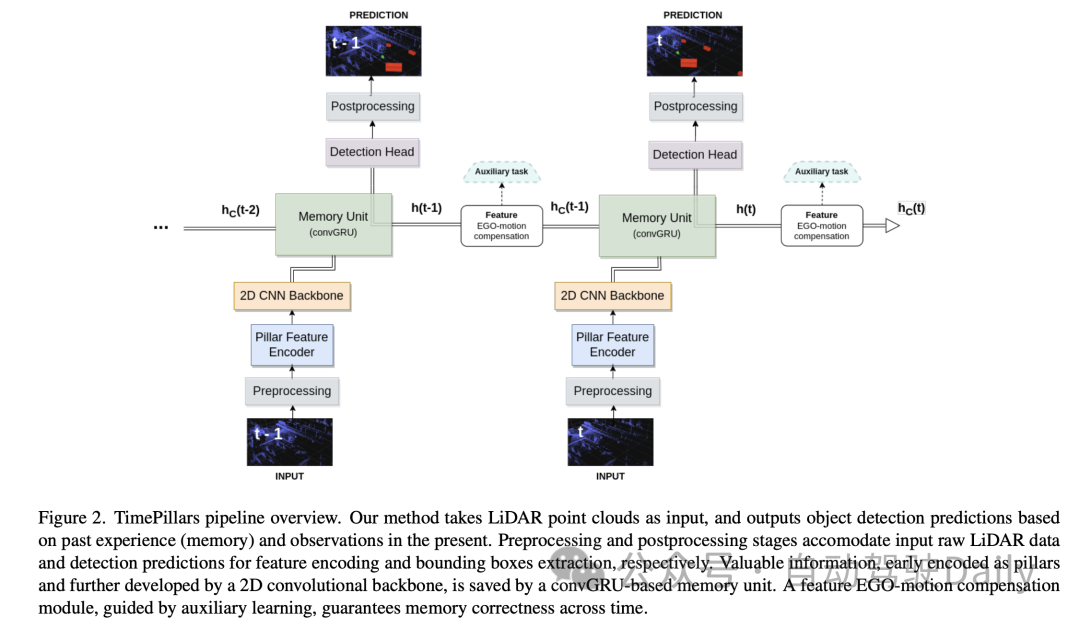
Artikel itu juga menyebut teknik lain untuk meningkatkan julat pengesanan, seperti lilitan jarang, modul perhatian dan lilitan 3D. Walau bagaimanapun, kaedah ini sering mengabaikan isu keserasian perkakasan sasaran. Apabila menggunakan dan melatih rangkaian saraf, perkakasan yang digunakan boleh berbeza dengan ketara dalam operasi dan kependaman yang disokong. Contohnya, perkakasan sasaran seperti Nvidia Orin DLA selalunya tidak menyokong operasi seperti lilitan atau perhatian yang jarang. Selain itu, menggunakan lapisan seperti lilitan 3D mungkin tidak dapat dilaksanakan kerana keperluan kependaman masa nyata. Oleh itu, menggunakan operasi mudah, seperti lilitan 2D, menjadi lebih perlu. Makalah ini mencadangkan model rekursif temporal baharu, TimePillars, yang menghormati set operasi yang disokong pada perkakasan sasaran biasa, bergantung pada lilitan 2D, berdasarkan perwakilan input tiang-titik (Tiang) dan unit rekursif konvolusi. Pampasan Pergerakan Kendiri digunakan pada keadaan tersembunyi unit berulang dengan bantuan satu lilitan dan pembelajaran tambahan. Penggunaan tugas tambahan untuk memastikan ketepatan manipulasi ini telah ditunjukkan melalui kajian ablasi adalah sesuai. Kertas kerja ini juga menyiasat penempatan optimum modul rekursif dalam saluran paip dan dengan jelas menunjukkan bahawa meletakkannya di antara tulang belakang rangkaian dan kepala pengesanan menghasilkan prestasi terbaik. Mengenai Zenseact Open Dataset (ZOD) yang baru dikeluarkan, kertas kerja menunjukkan keberkesanan kaedah TimePillars. Berbanding dengan garis dasar titik dan tiang bingkai tunggal dan berbilang bingkai, TimePillars mencapai peningkatan prestasi penilaian yang ketara, terutamanya pada pengesanan jarak jauh (sehingga 200 meter) dalam kategori penunggang basikal dan pejalan kaki yang penting. Akhir sekali, TimePillars mempunyai kependaman yang jauh lebih rendah daripada tiang titik berbilang bingkai, menjadikannya sesuai untuk sistem masa nyata.
Makalah ini mencadangkan model rekursif temporal baharu, TimePillars, yang menghormati set operasi yang disokong pada perkakasan sasaran biasa, bergantung pada lilitan 2D, berdasarkan perwakilan input tiang-titik (Tiang) dan unit rekursif konvolusi. Pampasan Pergerakan Kendiri digunakan pada keadaan tersembunyi unit berulang dengan bantuan satu lilitan dan pembelajaran tambahan. Penggunaan tugas tambahan untuk memastikan ketepatan manipulasi ini telah ditunjukkan melalui kajian ablasi adalah sesuai. Kertas kerja ini juga menyiasat penempatan optimum modul rekursif dalam saluran paip dan dengan jelas menunjukkan bahawa meletakkannya di antara tulang belakang rangkaian dan kepala pengesanan menghasilkan prestasi terbaik. Mengenai Zenseact Open Dataset (ZOD) yang baru dikeluarkan, kertas kerja menunjukkan keberkesanan kaedah TimePillars. Berbanding dengan garis dasar titik dan tiang bingkai tunggal dan berbilang bingkai, TimePillars mencapai peningkatan prestasi penilaian yang ketara, terutamanya pada pengesanan jarak jauh (sehingga 200 meter) dalam kategori penunggang basikal dan pejalan kaki yang penting. Akhir sekali, TimePillars mempunyai kependaman yang jauh lebih rendah daripada tiang titik berbilang bingkai, menjadikannya sesuai untuk sistem masa nyata.
Kertas kerja ini mencadangkan model rekursif temporal baharu yang dipanggil TimePillars untuk menyelesaikan tugas pengesanan objek lidar 3D. Berbanding dengan garis dasar tiang titik bingkai tunggal dan berbilang bingkai, TimePillars menunjukkan prestasi yang lebih baik dengan ketara dalam pengesanan jarak jauh dan menghormati set operasi yang disokong oleh perkakasan sasaran biasa. Kertas itu juga menanda aras model pengesanan objek lidar 3D pada dataset terbuka Zenseact baharu buat kali pertama. Walau bagaimanapun, batasan kertas adalah bahawa ia hanya mempertimbangkan data lidar, tanpa pertimbangan menyeluruh terhadap input sensor lain, dan pendekatannya adalah berdasarkan garis asas tunggal yang terkini. Walau bagaimanapun, pengarang percaya bahawa rangka kerja mereka adalah umum dan bahawa penambahbaikan masa depan kepada garis dasar akan membawa kepada peningkatan prestasi keseluruhan. 3. Kaedah

3.1 Prapemprosesan input
Dalam bahagian "prapemprosesan input" kertas ini, penulis menggunakan teknologi "Pillarisation" untuk memproses data awan titik input. Kaedah ini berbeza daripada vokselisasi konvensional, yang membahagikan awan titik kepada struktur kolumnar menegak hanya dalam arah mendatar (paksi x dan y) sambil mengekalkan ketinggian tetap dalam arah menegak (paksi z). Melakukannya memastikan dimensi input rangkaian konsisten dan membolehkan pemprosesan yang cekap menggunakan lilitan 2D.
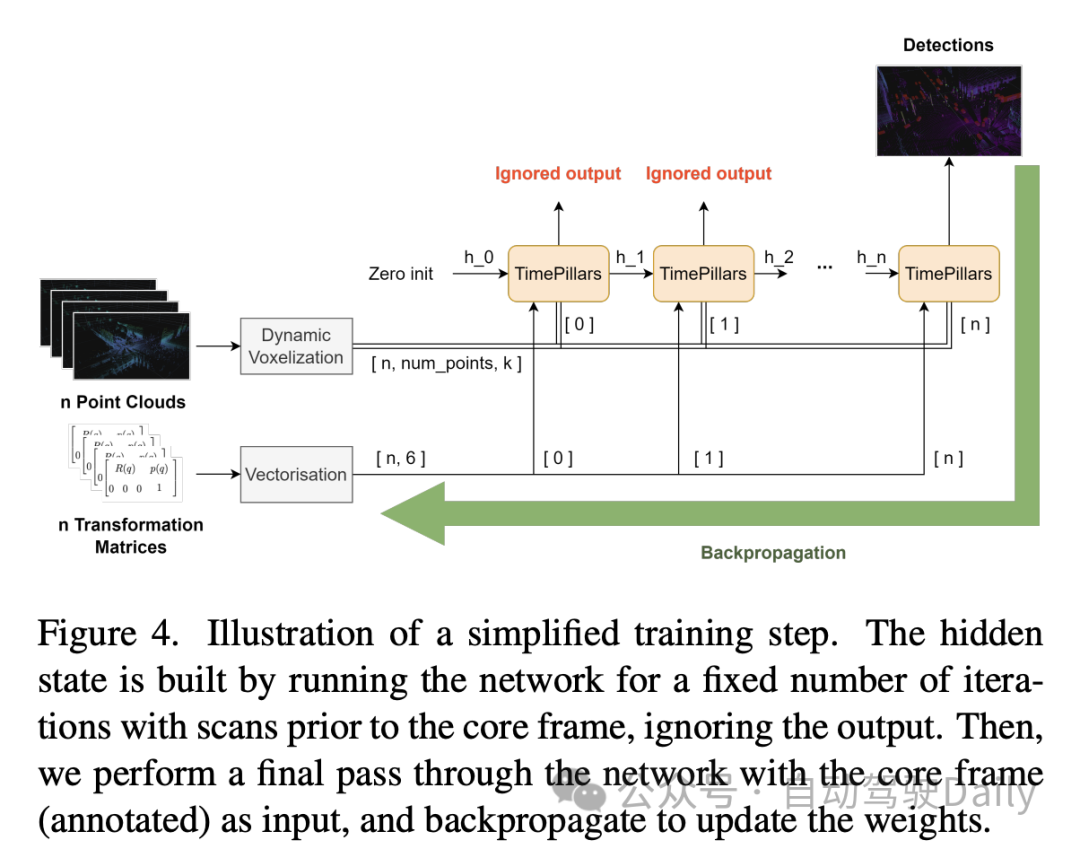
Walau bagaimanapun, satu masalah dengan Pilarisasi ialah ia menghasilkan banyak lajur kosong, mengakibatkan data yang sangat jarang. Untuk menyelesaikan masalah ini, makalah ini mencadangkan penggunaan teknologi voxelisasi dinamik. Teknik ini mengelakkan keperluan untuk mempunyai bilangan mata yang telah ditetapkan untuk setiap lajur, dengan itu menghapuskan keperluan untuk operasi pemotongan atau pengisian pada setiap lajur. Sebaliknya, keseluruhan data awan titik diproses secara keseluruhan untuk memadankan jumlah mata yang diperlukan, di sini ditetapkan kepada 200,000 mata. Faedah kaedah prapemprosesan ini ialah ia meminimumkan kehilangan maklumat dan menjadikan perwakilan data yang dihasilkan lebih stabil dan konsisten.
3.2 Seni bina model
Kemudian untuk seni bina Model, penulis memperkenalkan secara terperinci seni bina rangkaian saraf yang terdiri daripada Pengekod Ciri Pilar, tulang belakang Rangkaian Neural Konvolusi 2D (CNN) dan kepala pengesan.
-
Pillar Feature Encoder: Bahagian ini memetakan tensor input praproses ke dalam imej pseudo Bird's Eye View (BEV). Selepas menggunakan vokselisasi dinamik, PointNet yang dipermudahkan dilaraskan dengan sewajarnya. Input diproses oleh lilitan 1D, normalisasi kelompok dan fungsi pengaktifan ReLU, menghasilkan tensor bentuk , di mana mewakili bilangan saluran. Sebelum lapisan maksimum serakan terakhir, pengumpulan maksimum digunakan pada saluran, membentuk ruang terpendam bentuk . Oleh kerana tensor awal dikodkan sebagai , yang menjadi selepas lapisan sebelumnya, operasi pengumpulan maksimum dialih keluar.
-
Backbone: Menggunakan seni bina tulang belakang CNN 2D yang dicadangkan dalam kertas kolumnar asal kerana kecekapan kedalaman yang unggul. Ruang terpendam dikurangkan menggunakan tiga blok pensampelan bawah (Conv2D-BN-ReLU) dan dipulihkan menggunakan tiga blok pensampelan naik dan lilitan terbalik, dengan bentuk keluaran .
-
Unit Memori: Modelkan memori sistem sebagai rangkaian saraf berulang (RNN), khususnya menggunakan GRU (convGRU), yang merupakan versi konvolusi bagi Unit Berulang Berpagar. Kelebihan GRU konvolusi ialah ia mengelakkan masalah kecerunan yang hilang dan meningkatkan kecekapan sambil mengekalkan ciri data spatial. Berbanding dengan pilihan lain seperti LSTM, GRU mempunyai lebih sedikit parameter boleh dilatih kerana bilangan getnya yang lebih kecil dan boleh dianggap sebagai teknik regularisasi memori (mengurangkan kerumitan keadaan tersembunyi). Dengan menggabungkan operasi yang serupa, bilangan lapisan konvolusi yang diperlukan dikurangkan, menjadikan unit lebih cekap.
-
Kepala Pengesan: Pengubahsuaian ringkas kepada SSD (Pengesan MultiBox Pukulan Tunggal). Konsep teras SSD dikekalkan, iaitu pas tunggal tanpa cadangan wilayah, tetapi penggunaan kotak sauh dihapuskan. Mengeluarkan ramalan secara langsung untuk setiap sel dalam grid, walaupun kehilangan keupayaan pengesanan berbilang objek sel, mengelakkan pelarasan parameter kotak anchor yang membosankan dan selalunya tidak tepat dan memudahkan proses inferens. Lapisan linear mengendalikan keluaran klasifikasi dan penyetempatan (kedudukan, saiz dan sudut) regresi masing-masing. Hanya saiz yang menggunakan fungsi pengaktifan (ReLU) untuk mengelakkan mengambil nilai negatif. Di samping itu, tidak seperti kesusasteraan berkaitan, makalah ini mengelakkan masalah regresi sudut langsung dengan meramalkan komponen sinus dan kosinus arah pemanduan kenderaan secara bebas dan mengekstrak sudut daripadanya.
3.3 Pampasan Ego-Gerak Ciri
Dalam bahagian kertas ini, penulis membincangkan cara memproses output ciri keadaan tersembunyi oleh GRU konvolusi, yang diwakili oleh sistem koordinat bingkai sebelumnya. Jika disimpan terus dan digunakan untuk mengira ramalan seterusnya, ketidakpadanan spatial akan berlaku disebabkan oleh pergerakan ego.
Untuk penukaran, teknik yang berbeza boleh digunakan. Sebaik-baiknya, data yang diperbetulkan akan dimasukkan ke dalam rangkaian dan bukannya diubah dalam rangkaian. Walau bagaimanapun, ini bukan kaedah yang dicadangkan dalam kertas itu, kerana ia memerlukan penetapan semula keadaan tersembunyi pada setiap langkah dalam proses inferens, mengubah awan titik sebelumnya dan menyebarkannya ke seluruh rangkaian. Ini bukan sahaja tidak cekap, ia mengalahkan tujuan menggunakan RNN. Oleh itu, dalam konteks gelung, pampasan perlu dilakukan pada peringkat ciri. Ini menjadikan penyelesaian hipotesis lebih cekap, tetapi juga menjadikan masalah lebih kompleks. Kaedah interpolasi tradisional boleh digunakan untuk mendapatkan ciri dalam sistem koordinat yang diubah.
Sebaliknya, diilhamkan oleh kerja Chen et al., kertas kerja itu mencadangkan untuk menggunakan operasi konvolusi dan tugas tambahan untuk melaksanakan transformasi. Memandangkan butiran terhad kerja yang disebutkan di atas, kertas kerja mencadangkan penyelesaian yang disesuaikan untuk masalah ini.
Pendekatan yang diambil oleh kertas itu adalah untuk menyediakan rangkaian dengan maklumat yang diperlukan untuk melakukan transformasi ciri melalui lapisan konvolusi tambahan. Matriks penjelmaan relatif antara dua bingkai berturut-turut mula-mula dikira, iaitu operasi yang diperlukan untuk berjaya mengubah ciri. Kemudian, maklumat 2D (bahagian putaran dan terjemahan) diekstrak daripadanya:
Pemudahan ini mengelakkan pemalar matriks utama dan berfungsi dalam domain 2D (imej pseudo) 16, mengurangkan nilai 16 ke 6. Matriks kemudiannya diratakan dan dikembangkan untuk dipadankan dengan bentuk ciri tersembunyi yang akan diberi pampasan. Dimensi pertama mewakili bilangan bingkai yang perlu ditukar. Perwakilan ini menjadikannya sesuai untuk menggabungkan setiap tiang berpotensi dalam dimensi saluran ciri tersembunyi.
Akhir sekali, ciri keadaan tersembunyi dimasukkan ke dalam lapisan konvolusi 2D, yang disesuaikan dengan proses transformasi. Aspek utama yang perlu diberi perhatian ialah melakukan konvolusi tidak menjamin bahawa transformasi akan berlaku. Penggabungan saluran hanya menyediakan rangkaian maklumat tambahan tentang cara transformasi mungkin dilakukan. Dalam hal ini, penggunaan pembelajaran berbantu adalah sesuai. Semasa latihan, objektif pembelajaran tambahan (transformasi koordinat) ditambah selari dengan objektif utama (pengesan objek). Tugas tambahan direka bentuk yang tujuannya adalah untuk membimbing rangkaian melalui proses transformasi di bawah penyeliaan untuk memastikan ketepatan pampasan Tugas tambahan adalah terhad kepada proses latihan. Setelah rangkaian belajar mengubah ciri dengan betul, ia kehilangan kebolehgunaannya. Oleh itu, tugasan ini tidak dipertimbangkan semasa inferens. Dalam bahagian seterusnya eksperimen lanjut akan dijalankan untuk membandingkan kesannya.
4. Eksperimen

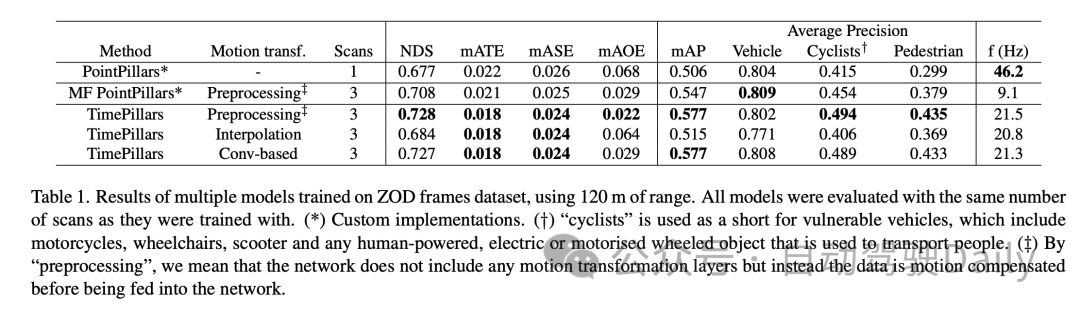
Hasil eksperimen menunjukkan bahawa model TimePillars berprestasi baik semasa memproses set data bingkai Zenseact Open Dataset (ZOD), terutamanya apabila memproses julat sehingga 120 meter. Keputusan ini menyerlahkan perbezaan prestasi TimePillars di bawah kaedah transformasi gerakan yang berbeza dan bandingkan dengan kaedah lain.
Selepas membandingkan PointPillars model garis dasar dan PointPillars berbilang bingkai (MF), dapat dilihat bahawa TimePillars telah mencapai peningkatan yang ketara dalam berbilang penunjuk prestasi utama. Terutama pada Skor Pengesanan NuScenes (NDS), TimePillars menunjukkan skor keseluruhan yang lebih tinggi, mencerminkan kelebihannya dalam prestasi pengesanan dan ketepatan kedudukan. Selain itu, TimePillars juga mencapai nilai yang lebih rendah dalam ralat penukaran purata (mATE), ralat skala purata (mASE) dan ralat orientasi purata (mAOE), menunjukkan bahawa ia lebih tepat dalam ketepatan kedudukan dan anggaran orientasi. Nota khusus ialah pelaksanaan TimePillars yang berbeza dari segi penukaran gerakan mempunyai kesan yang signifikan terhadap prestasi. Apabila menggunakan transformasi gerakan berasaskan lilitan (berasaskan Conv), TimePillars berprestasi baik pada NDS, mATE, mASE dan mAOE, membuktikan keberkesanan kaedah ini dalam pampasan gerakan dan meningkatkan ketepatan pengesanan. Sebaliknya, TimePillars menggunakan kaedah interpolasi juga mengatasi model garis dasar, tetapi lebih rendah daripada kaedah konvolusi dalam beberapa penunjuk. Keputusan ketepatan purata (mAP) menunjukkan bahawa TimePillars berprestasi baik dalam pengesanan kategori kenderaan, penunggang basikal dan pejalan kaki, terutamanya apabila berhadapan dengan kategori yang lebih mencabar seperti penunggang basikal dan pejalan kaki, peningkatan prestasinya adalah lebih ketara. Dari perspektif kekerapan pemprosesan (f (Hz)), walaupun TimePillars tidak sepantas PointPillars bingkai tunggal, ia lebih pantas daripada PointPillars berbilang bingkai sambil mengekalkan prestasi pengesanan yang tinggi. Ini menunjukkan bahawa TimePillars boleh melakukan pengesanan jarak jauh dan pampasan gerakan dengan berkesan sambil mengekalkan pemprosesan masa nyata. Dalam erti kata lain, model TimePillars menunjukkan kelebihan ketara dalam pengesanan jarak jauh, pampasan gerakan dan kelajuan pemprosesan, terutamanya apabila memproses data berbilang bingkai dan menggunakan teknologi penukaran gerakan berasaskan konvolusi. Keputusan ini menyerlahkan potensi aplikasi TimePillars dalam bidang pengesanan objek lidar 3D untuk kenderaan autonomi.

Keputusan percubaan di atas menunjukkan bahawa model TimePillars berprestasi cemerlang dalam prestasi pengesanan objek dalam julat jarak yang berbeza, terutamanya berbanding dengan model penanda aras PointPillars. Keputusan ini dibahagikan kepada tiga julat pengesanan utama: 0 hingga 50 meter, 50 hingga 100 meter dan ke atas 100 meter.
Pertama sekali, NuScenes Detection Score (NDS) dan Average Precision (mAP) ialah penunjuk prestasi keseluruhan. TimePillars mengatasi PointPillars pada kedua-dua metrik, menunjukkan keseluruhan keupayaan pengesanan yang lebih tinggi dan ketepatan kedudukan. Secara khusus, TimePillars' NDS ialah 0.723, yang jauh lebih tinggi daripada PointPillars' 0.657 dari segi mAP, TimePillars juga dengan ketara mengatasi PointPillars' 0.475 dengan 0.570.

Dalam perbandingan prestasi dalam julat jarak yang berbeza, dapat dilihat bahawa TimePillars berprestasi lebih baik dalam setiap julat. Bagi kategori kenderaan, ketepatan pengesanan TimePillars dalam julat 0 hingga 50 meter, 50 hingga 100 meter dan lebih 100 meter masing-masing ialah 0.884, 0.776 dan 0.591, yang semuanya lebih tinggi daripada prestasi PointPillars dalam julat yang sama. Ini menunjukkan bahawa TimePillars mempunyai ketepatan yang lebih tinggi dalam pengesanan kenderaan, baik pada jarak dekat dan jauh. TimePillars juga menunjukkan prestasi pengesanan yang lebih baik apabila berurusan dengan kenderaan yang terdedah (seperti motosikal, kerusi roda, skuter elektrik, dsb.). Terutamanya dalam julat lebih daripada 100 meter, ketepatan pengesanan TimePillars ialah 0.178, manakala PointPillars hanya 0.036, menunjukkan kelebihan ketara dalam pengesanan jarak jauh. Bagi pengesanan pejalan kaki, TimePillars juga menunjukkan prestasi yang lebih baik, terutamanya dalam julat 50 hingga 100 meter, dengan ketepatan pengesanan 0.350, manakala PointPillars hanya 0.211. Walaupun pada jarak yang lebih jauh (lebih 100 meter), TimePillars masih mencapai tahap pengesanan tertentu (ketepatan 0.032), manakala PointPillars melakukan sifar pada julat ini.
Keputusan percubaan ini menyerlahkan prestasi unggul TimePillars dalam mengendalikan tugas pengesanan objek dalam julat jarak yang berbeza. Sama ada pada jarak dekat atau pada jarak jauh yang lebih mencabar, TimePillars memberikan hasil pengesanan yang lebih tepat dan boleh dipercayai, yang penting untuk keselamatan dan kecekapan kenderaan autonomi.
5. Perbincangan

Pertama sekali, kelebihan utama model TimePillars ialah keberkesanannya untuk pengesanan objek jarak jauh. Dengan menggunakan vokselisasi dinamik dan struktur GRU konvolusi, model ini lebih mampu mengendalikan data lidar yang jarang, terutamanya dalam pengesanan objek jarak jauh. Ini penting untuk operasi selamat kenderaan autonomi dalam persekitaran jalan yang kompleks dan berubah-ubah. Di samping itu, model ini juga menunjukkan prestasi yang baik dari segi kelajuan pemprosesan, yang penting untuk aplikasi masa nyata. Sebaliknya, TimePillars menggunakan kaedah berasaskan konvolusi untuk Pampasan Pergerakan, yang merupakan peningkatan besar berbanding kaedah tradisional. Pendekatan ini memastikan ketepatan transformasi melalui tugas tambahan semasa latihan, meningkatkan ketepatan model semasa mengendalikan objek bergerak.
Walau bagaimanapun, penyelidikan kertas ini juga mempunyai beberapa batasan. Pertama, sementara TimePillars berprestasi baik dalam mengendalikan pengesanan objek jauh, peningkatan prestasi ini mungkin berlaku dengan mengorbankan beberapa kelajuan pemprosesan. Walaupun kelajuan model masih sesuai untuk aplikasi masa nyata, ia masih berkurangan berbanding kaedah bingkai tunggal. Di samping itu, kertas kerja ini tertumpu terutamanya pada data LiDAR dan tidak mempertimbangkan input sensor lain, seperti kamera atau radar, yang mungkin mengehadkan penggunaan model dalam persekitaran berbilang penderia yang lebih kompleks.
Maksudnya, TimePillars telah menunjukkan kelebihan ketara dalam pengesanan objek lidar 3D untuk kenderaan autonomi, terutamanya dalam pengesanan jarak jauh dan Pampasan Pergerakan. Walaupun terdapat sedikit pertukaran dalam kelajuan pemprosesan dan had dalam memproses data berbilang sensor, TimePillars masih mewakili kemajuan penting dalam bidang ini.
6. Kesimpulan
Kerja ini menunjukkan bahawa mengambil kira data sensor lepas adalah lebih baik daripada hanya menggunakan maklumat semasa. Mengakses maklumat persekitaran pemanduan terdahulu boleh mengatasi sifat jarang awan titik lidar dan membawa kepada ramalan yang lebih tepat. Kami menunjukkan bahawa rangkaian berulang sesuai sebagai cara untuk mencapai yang terakhir. Pemberian memori sistem membawa kepada penyelesaian yang lebih mantap berbanding kaedah pengagregatan awan titik yang mencipta perwakilan data yang lebih padat melalui pemprosesan yang meluas. Kaedah cadangan kami, TimePillars, melaksanakan cara untuk menyelesaikan masalah rekursif. Dengan hanya menambah tiga lapisan konvolusional tambahan pada proses inferens, kami menunjukkan bahawa blok binaan rangkaian asas adalah mencukupi untuk mencapai hasil yang ketara dan memastikan kecekapan sedia ada dan spesifikasi penyepaduan perkakasan dipenuhi. Untuk pengetahuan terbaik kami, kerja ini menyediakan hasil penanda aras pertama untuk tugas pengesanan objek 3D pada set data terbuka Zenseact yang baru diperkenalkan. Kami berharap kerja kami dapat menyumbang kepada jalan raya yang lebih selamat dan lebih mampan pada masa hadapan.

Pautan asal: https://mp.weixin.qq.com/s/94JQcvGXFWfjlDCT77gjlA



Atas ialah kandungan terperinci Meningkatkan keupayaan pengesanan dengan cekap: menembusi pengesanan sasaran kecil melebihi 200 meter. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!
Artikel berkaitan
Lihat lagi- Artikel tentang sistem membuat keputusan pemanduan berautonomi
- Teknologi pemanduan autonomi dan amalan sistem pengangkutan pintar yang dilaksanakan di Jawa
- Masalah pengesanan berbilang sasaran dalam teknologi pengesanan sasaran
- Sebarkan semuanya? 3DifFusionDet: Model resapan memasuki pengesanan sasaran 3D gabungan LV!
- Tesla sekali lagi memperbaharui teknologi pemanduan autonomi: memperkenalkan paparan pemandangan 3D untuk meningkatkan fungsi bantuan tempat letak kereta

