Pernahkah anda membuat jalur Mobius sendiri?
Jalur Möbius ialah struktur matematik yang pelik. Ia sebenarnya sangat mudah untuk membina permukaan satu sisi yang cantik, malah seorang kanak-kanak boleh menyiapkannya dengan mudah. Anda hanya perlu mengambil sekeping pita kertas, pintal sekali, dan rekatkan kedua-dua hujungnya. Walau bagaimanapun, jalur Möbius yang mudah dibuat sedemikian mempunyai ciri-ciri kompleks yang telah lama menarik minat ahli matematik. Baru-baru ini, penyelidik telah diganggu oleh soalan yang kelihatan mudah, iaitu, berapakah panjang minimum pita kertas yang diperlukan untuk membuat jalur Möbius? Richard Evan Schwartz dari Brown University berkata bahawa masalah ini tidak dapat diselesaikan untuk jalur Möbius kerana ia "terbenam" dan bukannya "direndam", bermakna ia tidak menembusi satu sama lain atau bersilang sendiri. Jalur Möbius sebenarnya ialah hologram, angka yang diunjurkan ke dalam ruang tiga dimensi: untuk jalur Möbius yang "direndam", beberapa lapisan jalur boleh bertindih antara satu sama lain, sedikit seperti hantu yang melalui dinding untuk Möbius "tertanam". jalur, tiada pertindihan sedemikian.  Pada tahun 1977, ahli matematik Charles Sidney Weaver dan Benjamin Rigler Halpern mengemukakan masalah dimensi minimum ini, dengan menyatakan bahawa ia adalah mudah jika jalur Möbius dibenarkan bersilang sendiri. Masalah yang tinggal, kemudian, adalah untuk menentukan berapa banyak ruang yang diperlukan untuk mengelakkan persimpangan diri. Halpern dan Weaver mencadangkan saiz minimum, tetapi mereka tidak dapat membuktikan idea itu, jadi ia dikenali sebagai sangkaan Halpern-Weaver. Schwartz mula-mula mengetahui tentang masalah ini empat tahun lalu dan terpesona dengannya sebaik sahaja dia mengetahuinya. Kini, minatnya telah bertukar menjadi buah baru. Alamat kertas: https://arxiv.org/pdf/2308.12641.pdfDia membuktikan Halpern dalam kertas pracetak yang disiarkan di arXiv.org pada 24 Ogos, 20233ure. Dia menunjukkan bahawa jalur Möbius "terbenam" yang diperbuat daripada kertas hanya boleh dibina dengan nisbah bidang lebih besar daripada
Pada tahun 1977, ahli matematik Charles Sidney Weaver dan Benjamin Rigler Halpern mengemukakan masalah dimensi minimum ini, dengan menyatakan bahawa ia adalah mudah jika jalur Möbius dibenarkan bersilang sendiri. Masalah yang tinggal, kemudian, adalah untuk menentukan berapa banyak ruang yang diperlukan untuk mengelakkan persimpangan diri. Halpern dan Weaver mencadangkan saiz minimum, tetapi mereka tidak dapat membuktikan idea itu, jadi ia dikenali sebagai sangkaan Halpern-Weaver. Schwartz mula-mula mengetahui tentang masalah ini empat tahun lalu dan terpesona dengannya sebaik sahaja dia mengetahuinya. Kini, minatnya telah bertukar menjadi buah baru. Alamat kertas: https://arxiv.org/pdf/2308.12641.pdfDia membuktikan Halpern dalam kertas pracetak yang disiarkan di arXiv.org pada 24 Ogos, 20233ure. Dia menunjukkan bahawa jalur Möbius "terbenam" yang diperbuat daripada kertas hanya boleh dibina dengan nisbah bidang lebih besar daripada  . Contohnya, jika panjang tali ialah 1 cm, lebarnya mestilah lebih besar daripada
. Contohnya, jika panjang tali ialah 1 cm, lebarnya mestilah lebih besar daripada  cm. Menyelesaikan teka-teki ini memerlukan kreativiti matematik. Apabila seseorang mengambil pendekatan standard untuk menyelesaikan jenis masalah ini, sukar untuk membezakan antara permukaan bersilang sendiri dan tidak bersilang sendiri melalui formula. Ia memerlukan penglihatan geometri Schwartz untuk mengatasi kesukaran ini, tetapi ini jarang berlaku. Dalam bukti Schwartz, dia berjaya memecahkan masalah itu kepada bahagian yang boleh diurus, yang setiap satunya hanya memerlukan pengetahuan asas geometri untuk diselesaikan. Malah, Schwartz mencuba strategi lain secara aktif dan luar selama beberapa tahun sebelum menemui strategi yang berkesan. Dia baru-baru ini memutuskan untuk menyemak semula masalah itu kerana dia sentiasa merasakan bahawa kaedah yang dia gunakan dalam kertas 2021 sepatutnya sah. Jelas sekali, gerak hati dia betul. Apabila dia melihat semula masalah itu, dia melihat ralat dalam lemma yang melibatkan carta-T dalam kertas sebelumnya. Dengan membetulkan kesilapan ini, Schwartz dengan cepat dan mudah membuktikan sangkaan Halpern-Weaver. Schwartz sendiri mengatakan bahawa jika tidak kerana kesilapan itu, dia akan menyelesaikan masalah itu tiga tahun lalu.
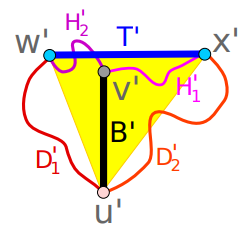
cm. Menyelesaikan teka-teki ini memerlukan kreativiti matematik. Apabila seseorang mengambil pendekatan standard untuk menyelesaikan jenis masalah ini, sukar untuk membezakan antara permukaan bersilang sendiri dan tidak bersilang sendiri melalui formula. Ia memerlukan penglihatan geometri Schwartz untuk mengatasi kesukaran ini, tetapi ini jarang berlaku. Dalam bukti Schwartz, dia berjaya memecahkan masalah itu kepada bahagian yang boleh diurus, yang setiap satunya hanya memerlukan pengetahuan asas geometri untuk diselesaikan. Malah, Schwartz mencuba strategi lain secara aktif dan luar selama beberapa tahun sebelum menemui strategi yang berkesan. Dia baru-baru ini memutuskan untuk menyemak semula masalah itu kerana dia sentiasa merasakan bahawa kaedah yang dia gunakan dalam kertas 2021 sepatutnya sah. Jelas sekali, gerak hati dia betul. Apabila dia melihat semula masalah itu, dia melihat ralat dalam lemma yang melibatkan carta-T dalam kertas sebelumnya. Dengan membetulkan kesilapan ini, Schwartz dengan cepat dan mudah membuktikan sangkaan Halpern-Weaver. Schwartz sendiri mengatakan bahawa jika tidak kerana kesilapan itu, dia akan menyelesaikan masalah itu tiga tahun lalu.  . Lemma ini berdasarkan idea asas: beberapa garis lurus pada jalur Möbius dipanggil permukaan yang diperintah. Schwartz menegaskan bahawa jalur kertas di angkasa, walaupun ia berada dalam beberapa kedudukan yang rumit, masih mempunyai garis lurus yang melaluinya pada setiap titik Anda boleh bayangkan melukis garis lurus ini supaya ia melintasi jalur Möbius dan Kedua-dua hujungnya bersentuhan sempadan.Dalam kerja sebelum ini, Schwartz mengenal pasti dua garis lurus selari antara satu sama lain dan dalam satah yang sama, yang membentuk corak berbentuk T dalam setiap jalur Möbius. Beliau menegaskan bahawa perkara-perkara ini tidak jelas wujud dan ia perlu dibuktikan, yang merupakan bahagian pertama untuk membuktikan lemma. Langkah seterusnya ialah menyediakan dan menyelesaikan masalah pengoptimuman, yang memerlukan pemotongan jalur Möbius pada sudut di sepanjang segmen garisan memanjangkan lebar jalur dan mendapatkan bentuk akhir. Schwartz tersilap membuat kesimpulan dalam kertas tahun 2021 bahawa bentuk itu ialah segi empat selari. Musim panas ini, Schwartz memutuskan untuk mencuba strategi yang berbeza. Dia mula cuba meratakan jalur Möbius. Jika boleh ditunjukkan bahawa ia boleh ditekan ke permukaan rata, masalah kompleks ini akan dikurangkan kepada masalah permukaan rata yang lebih mudah dikendalikan. Dalam eksperimen, Schwartz memotong jalur Möbius dan menyedari bahawa ia bukan segi empat selari tetapi trapezium. Akhirnya terjawab juga soalan 50 tahun itu. Ia memerlukan keberanian untuk cuba menyelesaikan masalah yang telah lama wujud, dan ini adalah kekuatan Schwartz dalam matematik: dia suka menyelesaikan masalah yang kelihatan agak mudah tetapi sebenarnya sukar. Dia akan melihat masalah yang pengkaji terdahulu tidak perasan. Pautan rujukan: https://www.scientificamerican.com/article/mathematicians-solve-50-year-old-moebius-strip-puzzle1/
. Lemma ini berdasarkan idea asas: beberapa garis lurus pada jalur Möbius dipanggil permukaan yang diperintah. Schwartz menegaskan bahawa jalur kertas di angkasa, walaupun ia berada dalam beberapa kedudukan yang rumit, masih mempunyai garis lurus yang melaluinya pada setiap titik Anda boleh bayangkan melukis garis lurus ini supaya ia melintasi jalur Möbius dan Kedua-dua hujungnya bersentuhan sempadan.Dalam kerja sebelum ini, Schwartz mengenal pasti dua garis lurus selari antara satu sama lain dan dalam satah yang sama, yang membentuk corak berbentuk T dalam setiap jalur Möbius. Beliau menegaskan bahawa perkara-perkara ini tidak jelas wujud dan ia perlu dibuktikan, yang merupakan bahagian pertama untuk membuktikan lemma. Langkah seterusnya ialah menyediakan dan menyelesaikan masalah pengoptimuman, yang memerlukan pemotongan jalur Möbius pada sudut di sepanjang segmen garisan memanjangkan lebar jalur dan mendapatkan bentuk akhir. Schwartz tersilap membuat kesimpulan dalam kertas tahun 2021 bahawa bentuk itu ialah segi empat selari. Musim panas ini, Schwartz memutuskan untuk mencuba strategi yang berbeza. Dia mula cuba meratakan jalur Möbius. Jika boleh ditunjukkan bahawa ia boleh ditekan ke permukaan rata, masalah kompleks ini akan dikurangkan kepada masalah permukaan rata yang lebih mudah dikendalikan. Dalam eksperimen, Schwartz memotong jalur Möbius dan menyedari bahawa ia bukan segi empat selari tetapi trapezium. Akhirnya terjawab juga soalan 50 tahun itu. Ia memerlukan keberanian untuk cuba menyelesaikan masalah yang telah lama wujud, dan ini adalah kekuatan Schwartz dalam matematik: dia suka menyelesaikan masalah yang kelihatan agak mudah tetapi sebenarnya sukar. Dia akan melihat masalah yang pengkaji terdahulu tidak perasan. Pautan rujukan: https://www.scientificamerican.com/article/mathematicians-solve-50-year-old-moebius-strip-puzzle1/Atas ialah kandungan terperinci Berapakah panjang minimum pita kertas yang diperlukan untuk membuat jalur Möbius? Misteri berusia 50 tahun diselesaikan. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!


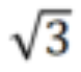 . Contohnya, jika panjang tali ialah 1 cm, lebarnya mestilah lebih besar daripada
. Contohnya, jika panjang tali ialah 1 cm, lebarnya mestilah lebih besar daripada  cm.
cm.