Rumah >Peranti teknologi >AI >Melalui MAmmoT, LLM menjadi generalis matematik: daripada logik formal kepada empat operasi aritmetik
Melalui MAmmoT, LLM menjadi generalis matematik: daripada logik formal kepada empat operasi aritmetik
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBke hadapan
- 2023-09-25 13:53:121447semak imbas
Penaakulan matematik ialah keupayaan penting model bahasa besar moden (LLM). Walaupun terdapat beberapa kemajuan terkini dalam bidang ini, masih terdapat jurang yang jelas antara sumber tertutup dan LLM sumber terbuka. Model sumber tertutup seperti GPT-4, PaLM-2 dan Claude 2 mendominasi penanda aras penaakulan matematik biasa seperti GSM8K dan MATH, manakala model sumber terbuka seperti Llama, Falcon dan OPT ketinggalan dengan ketara pada semua penanda aras
Untuk menyelesaikan Mengenai isu ini, komuniti penyelidik bekerja dalam dua arah
(1) Kaedah pra-latihan berterusan seperti Galactica dan MINERVA boleh melatih LLM secara berterusan berdasarkan lebih daripada 100 bilion data rangkaian berkaitan matematik. Kaedah ini boleh meningkatkan keupayaan penaakulan saintifik umum model, tetapi kos pengiraan lebih tinggi
Kaedah penalaan halus set data khusus seperti penalaan halus pensampelan penolakan (RFT) dan WizardMath, yang menggunakan data diselia daripada set data tertentu untuk memperhalusi LLM. Walaupun kaedah ini boleh meningkatkan prestasi dalam domain tertentu, kaedah ini tidak digeneralisasikan kepada tugas penaakulan matematik yang lebih luas di luar data penalaan halus. Sebagai contoh, RFT dan WizardMath boleh meningkatkan ketepatan lebih daripada 30% pada GSM8K (salah satunya ialah set data yang diperhalusi), tetapi menjejaskan ketepatan pada set data di luar domain seperti MMLU-Math dan AQuA, menjadikannya lebih rendah As sebanyak 10%
Baru-baru ini, pasukan penyelidik dari institusi seperti University of Waterloo dan Ohio State University telah mencadangkan kaedah penalaan halus arahan matematik yang ringan tetapi boleh digeneralisasikan yang boleh digunakan untuk meningkatkan keluasan LLM (iaitu tidak Terhad untuk menyempurnakan tugasan) keupayaan penaakulan matematik.
Kandungan yang ditulis semula: Pada masa lalu, kaedah fokus terutamanya kaedah rantaian pemikiran (CoT), iaitu menyelesaikan masalah matematik melalui penerangan bahasa semula jadi langkah demi langkah. Kaedah ini sangat umum dan boleh digunakan untuk kebanyakan disiplin matematik, tetapi terdapat beberapa kesukaran dalam ketepatan pengiraan dan proses penaakulan matematik atau algoritma yang kompleks (seperti menyelesaikan punca persamaan kuadratik dan mengira nilai eigen matriks)
Sebagai perbandingan Seterusnya, kaedah reka bentuk segera format kod seperti Program of Thought (PoT) dan PAL menggunakan alat luaran (iaitu, jurubahasa Python) untuk memudahkan proses penyelesaian matematik. Pendekatan ini adalah untuk memunggah proses pengiraan kepada penterjemah Python luaran untuk menyelesaikan penaakulan matematik dan algoritma yang kompleks (seperti menyelesaikan persamaan kuadratik menggunakan sympy atau pengkomputeran nilai eigen matriks menggunakan numpy). Walau bagaimanapun, PoT bergelut dengan senario penaakulan yang lebih abstrak, seperti penaakulan akal, logik formal dan algebra abstrak, terutamanya tanpa API terbina dalam.
Untuk mengambil kira kelebihan kedua-dua kaedah CoT dan PoT, pasukan memperkenalkan set data penalaan halus arahan hibrid matematik baharu MathInstruct, yang mempunyai dua ciri utama: (1) Meliputi secara meluas bidang matematik yang berbeza dan Ijazah kompleks , (2) Gabungan prinsip CoT dan PoT
MathInstruct adalah berdasarkan tujuh set data prinsip matematik sedia ada dan enam set data yang baru disusun. Mereka menggunakan MathInstruct untuk memperhalusi model Llama dengan saiz yang berbeza (dari 7B hingga 70B). Mereka memanggil model yang terhasil sebagai model MAmmoTH, dan mendapati bahawa MAmmoTH mempunyai keupayaan yang tidak pernah berlaku sebelum ini, seperti generalis matematik.
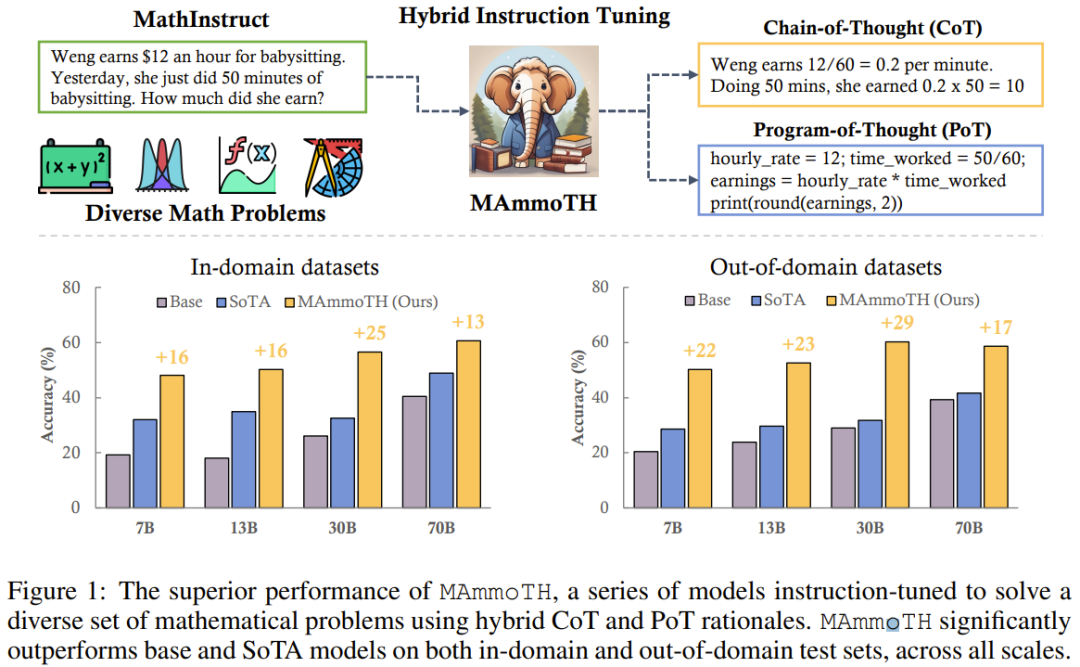
Untuk menilai MAmmoTH, pasukan penyelidik menggunakan satu siri set data penilaian, termasuk set ujian dalam domain (GSM8K, MATH, AQuA-RAT, NumGLUE) dan set ujian di luar domain (SVAMP, SAT, MMLU-Math, Mathematics, SimulEq)
Hasil penyelidikan menunjukkan bahawa model MAmmoTH berprestasi lebih baik dalam generalisasi kepada set data luar domain, dan juga meningkatkan dengan ketara keupayaan LLM sumber terbuka dalam penaakulan matematik
Perlu diingat bahawa pada set data MATH peringkat persaingan yang biasa digunakan, versi 7B MAmmoTH dapat mengalahkan WizardMath (yang merupakan model sumber terbuka terbaik sebelumnya pada MATH) sebanyak 3.5 kali (35.2% vs 10.7%), dan selepas penalaan halus 34B MAmmoTH-Coder malah boleh melebihi GPT-4 menggunakan CoT
Sumbangan penyelidikan ini boleh diringkaskan dalam dua aspek: (1) Dari segi kejuruteraan data, mereka mencadangkan pengajaran matematik berkualiti tinggi set data penalaan halus , yang mengandungi pelbagai masalah matematik yang berbeza dan prinsip pencampuran. (2) Dari segi pemodelan, mereka melatih dan menilai lebih daripada 50 model baharu dan model asas yang berbeza dalam julat saiz dari 7B hingga 70B untuk meneroka kesan sumber data dan format input-output yang berbeza
Hasil penyelidikan menunjukkan bahawa , Model baharu seperti MAmmoTH dan MAmmoTH-Coder dengan ketara mengatasi model sumber terbuka terdahulu dari segi ketepatan

- Kertas: https://arxiv.org/pdf/2309.05653.pdf
- Kod: https://github.com/TIGER-AI-Lab/MAmmoTH
- Data model: https://huggingface.co/datasets/TIGER-Lab/MathInstruct
Pasukan telah mengeluarkan set data yang mereka susun dan sumber terbuka kod kaedah baharu dan mengeluarkannya pada Hugging Face di masa yang sama Pasukan berhasrat untuk menyusun senarai set data penalaan halus arahan matematik yang berkualiti tinggi dan pelbagai harus mempunyai dua ciri utama: (1) secara meluas meliputi domain matematik yang berbeza dan tahap kerumitan, dan (2) menggabungkan prinsip CoT dan PoT.
Untuk ciri pertama, para penyelidik mula-mula memilih beberapa set data berkualiti tinggi yang digunakan secara meluas meliputi medan matematik dan tahap kerumitan yang berbeza, seperti GSM8K, MATH, AQuA, Camel dan TheoremQA. Mereka kemudian menyedari kekurangan matematik peringkat kolej, seperti algebra abstrak dan logik formal, dalam set data sedia ada. Untuk menyelesaikan masalah ini, mereka menggunakan sebilangan kecil contoh benih yang terdapat dalam talian, mensintesis prinsip CoT bagi soalan dalam TheoremQA menggunakan GPT-4, dan mencipta pasangan "soalan-CoT" dengan cara berpandu sendiri
Untuk ciri kedua, menggabungkan prinsip CoT dan PoT boleh meningkatkan kepelbagaian set data, menjadikan model yang dilatihnya mampu menyelesaikan pelbagai jenis masalah matematik. Walau bagaimanapun, kebanyakan set data sedia ada menyediakan rasional prosedur yang terhad, mengakibatkan ketidakseimbangan antara prinsip CoT dan PoT. Untuk tujuan ini, pasukan menggunakan GPT-4 untuk menambah prinsip PoT untuk set data terpilih, termasuk MATH, AQuA, GSM8K dan TheoremQA. Program yang disintesis GPT-4 ini kemudiannya ditapis dengan membandingkan hasil pelaksanaannya dengan kebenaran asas beranotasi manusia, memastikan bahawa hanya prinsip berkualiti tinggi ditambahkan.
Mengikut garis panduan ini, mereka mencipta set data baharu MathInstruct, seperti yang diperincikan dalam Jadual 1 di bawah.
Ia mengandungi 260,000 pasangan (arahan, tindak balas), meliputi pelbagai bidang teras matematik (aritmetik, algebra, kebarangkalian, kalkulus dan geometri, dsb.), termasuk campuran prinsip CoT dan PoT, dan mempunyai prinsip CoT dan PoT yang berbeza, dan bahasa dan kesukaran.
Tetapkan semula latihan
Semua subset MathInstruct disatukan ke dalam struktur yang serupa dengan set data arahan Alpaca. Operasi penormalan ini memastikan model diperhalusi yang terhasil boleh mengendalikan data secara konsisten, tanpa mengira format set data asal 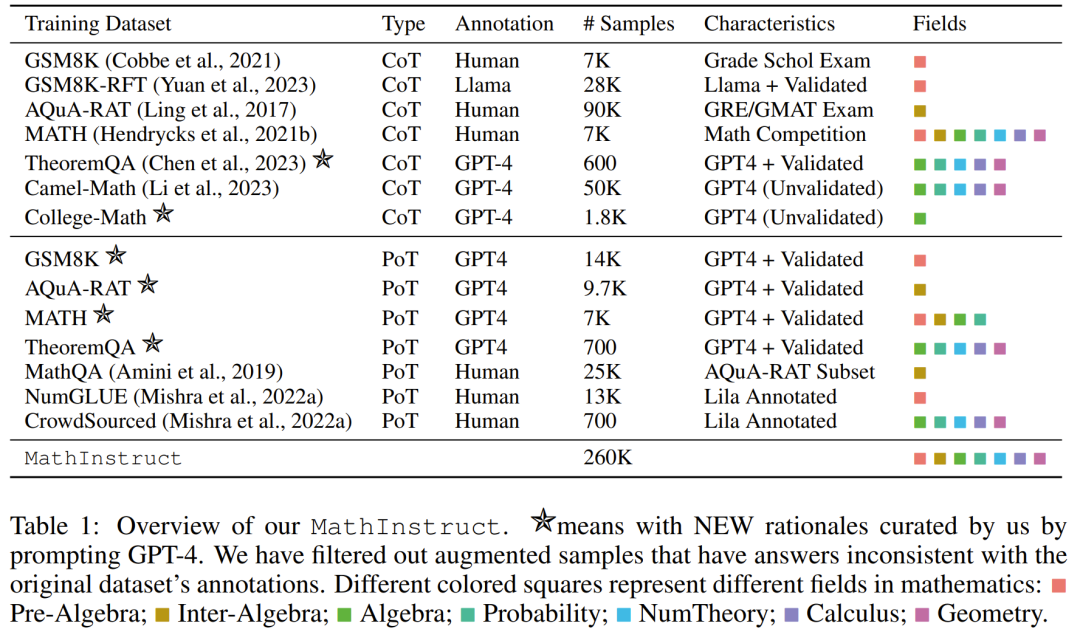
Untuk model asas, pasukan memilih Llama-2 dan Kod Llama
melalui MathInstruct Untuk pelarasan, mereka memperoleh model saiz yang berbeza, termasuk 7B, 13B, 34B dan 70B
Eksperimen
Set Data Penilaian
Eksperimen
Set Data Penilaian
penilaian model yang dipilih oleh pasukan yang dipilih. set, lihat Jadual 2 di bawah, mengandungi banyak sampel dalam medan dan luar medan yang berbeza, merangkumi beberapa bidang matematik yang berbeza. 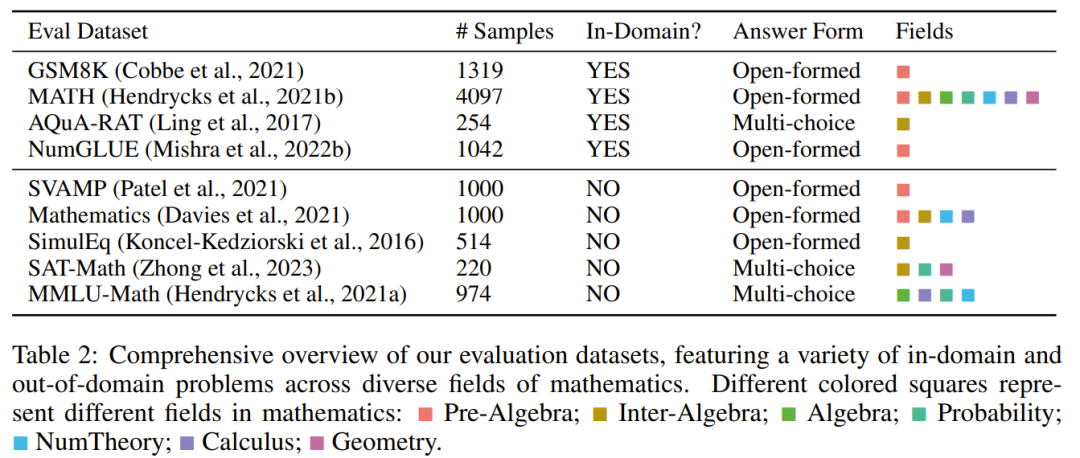
Set data penilaian mengandungi tahap kesukaran yang berbeza, termasuk peringkat rendah, menengah dan universiti. Sesetengah set data juga termasuk logik formal dan penaakulan akal
Setset penilaian yang dipilih mempunyai kedua-dua soalan terbuka dan aneka pilihan.
Untuk masalah terbuka (seperti GSM8K dan MATH), penyelidik menggunakan penyahkodan PoT kerana kebanyakan masalah ini boleh diselesaikan secara pemrograman. ,
Untuk soalan aneka pilihan (seperti AQuA dan MMLU), penyelidik menggunakan penyahkodan CoT kerana kebanyakan soalan dalam set data ini boleh dikendalikan dengan lebih baik oleh CoT.
Penyahkodan CoT tidak memerlukan sebarang perkataan pencetus, manakala penyahkodan PoT memerlukan perkataan pencetus: "Mari kita tulis program untuk menyelesaikan masalah".
Keputusan utama🎜 Jadual 3 dan 4 di bawah masing-masing melaporkan keputusan mengenai data di dalam dan di luar domain. 🎜🎜
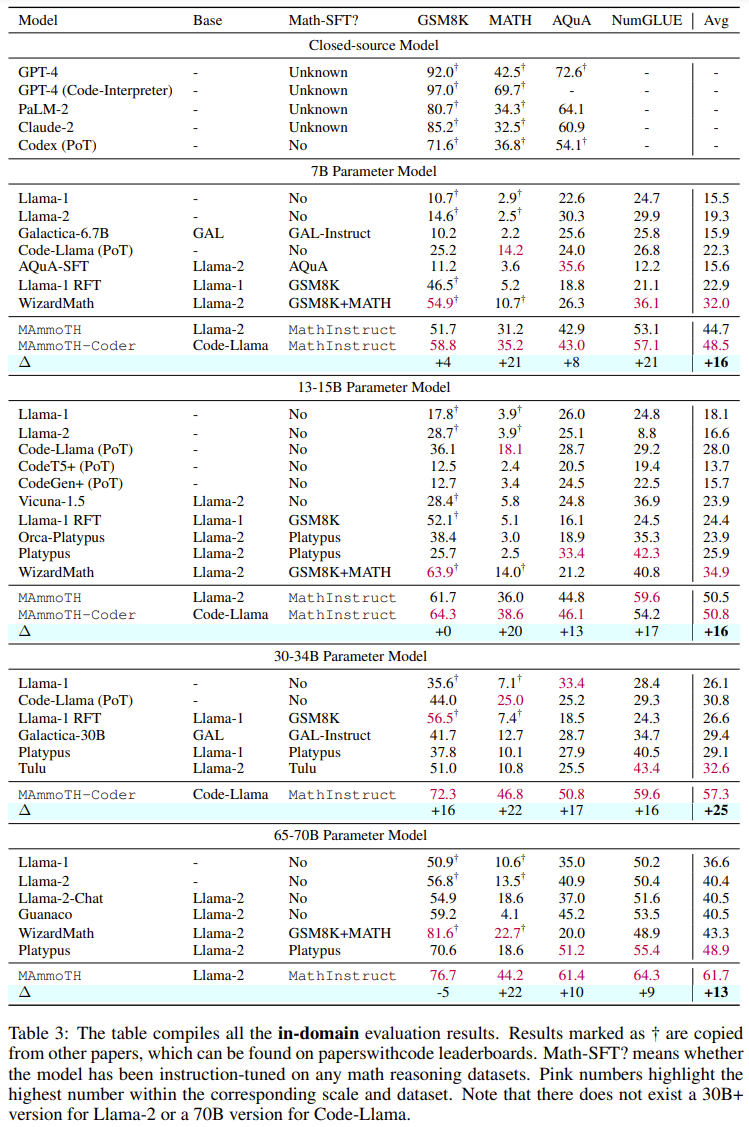
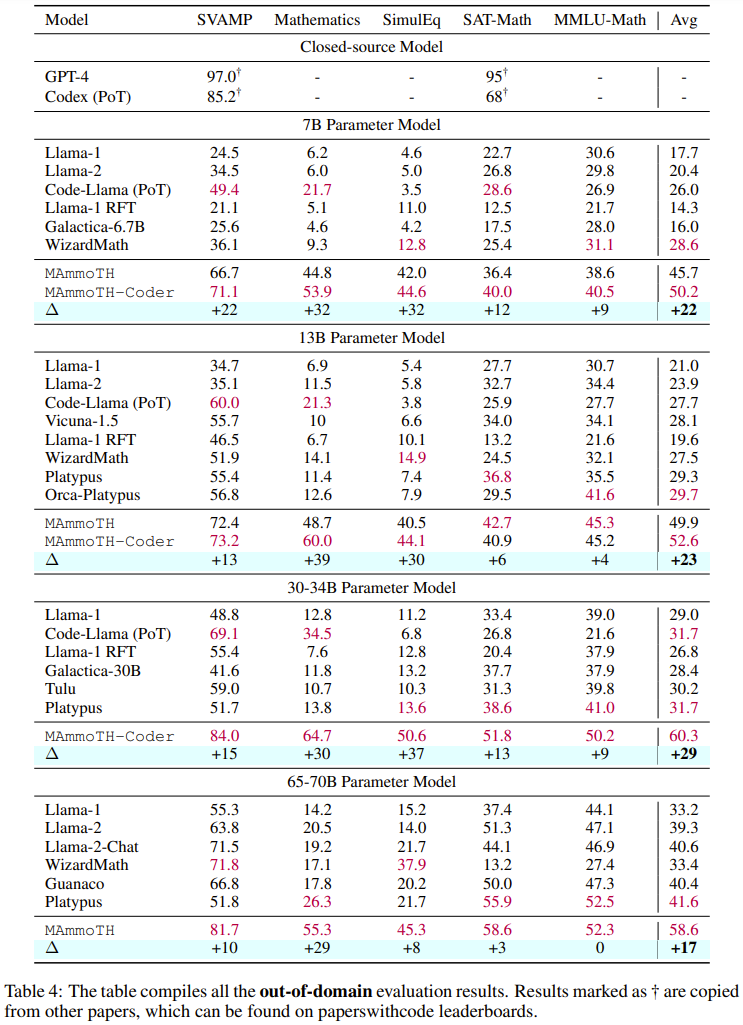
Secara keseluruhan, kedua-dua MAmmoTH dan MAmmoTH-Coder mengatasi model terbaik sebelumnya pada saiz model yang berbeza. Model baharu mencapai lebih banyak keuntungan prestasi pada set data luar domain berbanding set data dalam domain. Keputusan ini menunjukkan bahawa model baharu itu memang berpotensi untuk menjadi generalis matematik. MAmmoTH-Coder-34B dan MAmmoTH-70B malah mengatasi LLM sumber tertutup pada beberapa set data.
Para penyelidik juga membandingkan menggunakan model asas yang berbeza. Secara khusus, mereka menjalankan eksperimen membandingkan dua model asas, Llama-2 dan Code-Llama. Seperti yang dapat dilihat daripada dua jadual di atas, Code-Llama secara keseluruhan lebih baik daripada Llama-2, terutamanya pada set data luar medan. Jurang antara MAmmoTH dan MAmmoTH-Coder bahkan boleh mencapai 5%
Penerokaan penyelidikan ablasi mengenai sumber data
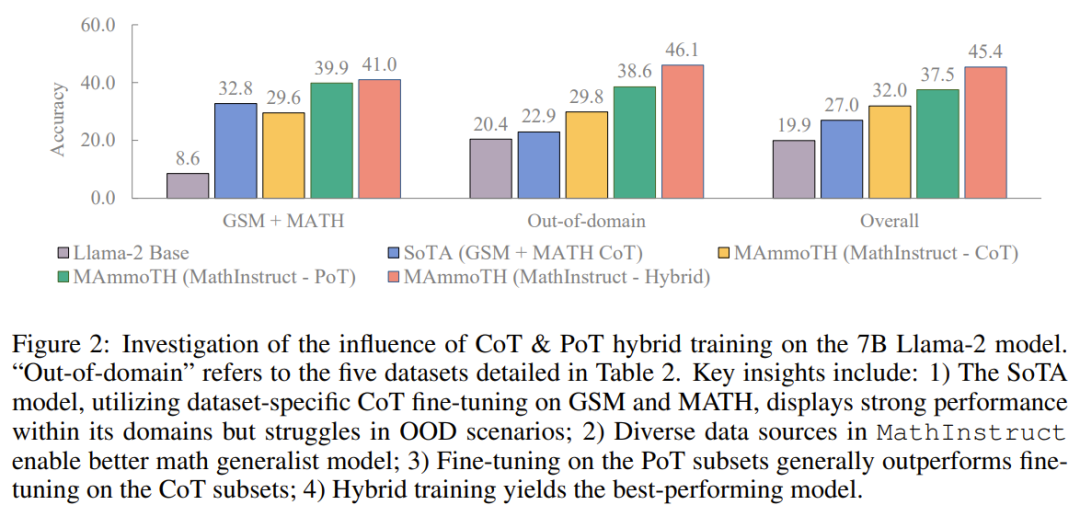
Mereka menjalankan penyelidikan untuk meneroka sumber keuntungan prestasi. Untuk lebih memahami sumber kelebihan MAmmoTH berbanding model penanda aras sedia ada, para penyelidik menjalankan satu siri eksperimen terkawal. Hasilnya ditunjukkan dalam Rajah 2. Secara ringkasnya, kelebihan prestasi ketara MAmmoTH boleh dikaitkan dengan : 1) Sumber data yang pelbagai meliputi. domain matematik yang berbeza dan tahap kerumitan, 2) Strategi hibrid untuk penalaan halus arahan CoT dan PoT.
 Mereka juga mengkaji kesan subset utama. Berkenaan dengan pelbagai sumber MathInstruct yang digunakan untuk melatih MAmmoTH, adalah penting juga untuk memahami sejauh mana setiap sumber menyumbang kepada prestasi keseluruhan model. Mereka menumpukan pada empat subset utama: GSM8K, MATH, Camel dan AQuA. Mereka menjalankan percubaan di mana setiap set data ditambahkan secara beransur-ansur pada latihan dan membandingkan prestasi dengan model yang diperhalusi pada keseluruhan MathInstruct.
Mereka juga mengkaji kesan subset utama. Berkenaan dengan pelbagai sumber MathInstruct yang digunakan untuk melatih MAmmoTH, adalah penting juga untuk memahami sejauh mana setiap sumber menyumbang kepada prestasi keseluruhan model. Mereka menumpukan pada empat subset utama: GSM8K, MATH, Camel dan AQuA. Mereka menjalankan percubaan di mana setiap set data ditambahkan secara beransur-ansur pada latihan dan membandingkan prestasi dengan model yang diperhalusi pada keseluruhan MathInstruct.
Menurut keputusan dalam Jadual 5, dapat dilihat bahawa jika kepelbagaian set data latihan tidak mencukupi (contohnya, apabila terdapat hanya GSM8K), keupayaan generalisasi model adalah sangat lemah: model hanya boleh menyesuaikan diri dengan situasi dalam pengagihan data , sukar untuk menyelesaikan masalah di luar masalah GSM
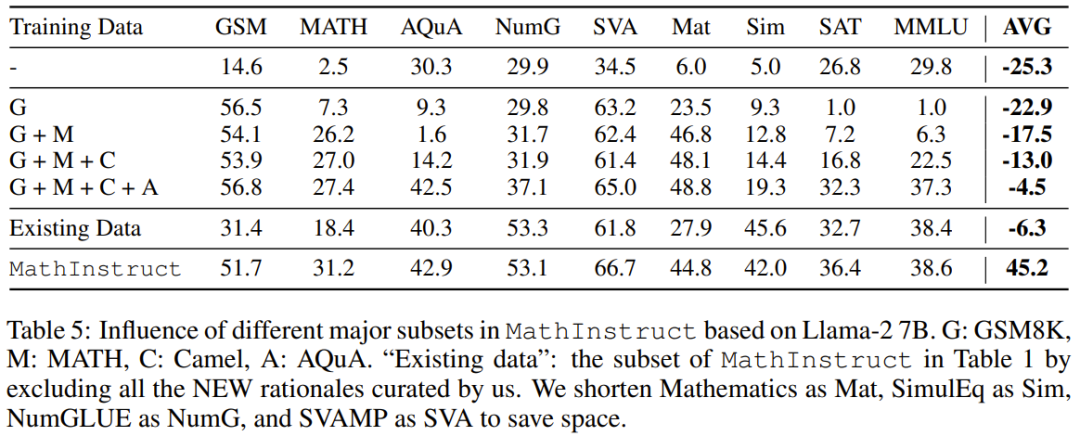 Impak penting sumber data yang pelbagai pada MAmmoTH diserlahkan dalam keputusan ini, yang juga merupakan kunci teras kepada menjadikan MAmmoTH seorang generalis matematik. Keputusan ini juga memberikan pandangan dan panduan yang berharga untuk usaha penyusunan data dan pengumpulan data masa hadapan kami, contohnya kami harus sentiasa mengumpul data yang pelbagai dan mengelak daripada mengumpul hanya jenis data tertentu
Impak penting sumber data yang pelbagai pada MAmmoTH diserlahkan dalam keputusan ini, yang juga merupakan kunci teras kepada menjadikan MAmmoTH seorang generalis matematik. Keputusan ini juga memberikan pandangan dan panduan yang berharga untuk usaha penyusunan data dan pengumpulan data masa hadapan kami, contohnya kami harus sentiasa mengumpul data yang pelbagai dan mengelak daripada mengumpul hanya jenis data tertentu
Atas ialah kandungan terperinci Melalui MAmmoT, LLM menjadi generalis matematik: daripada logik formal kepada empat operasi aritmetik. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!

