Bilangan segi tiga sama kaki dalam pokok binari

Pohon binari ialah struktur data di mana setiap nod boleh mempunyai sehingga dua nod anak. Kanak-kanak ini dipanggil anak kiri dan anak kanan masing-masing. Katakan kita diberi perwakilan tatasusunan induk, anda perlu menggunakannya untuk mencipta pokok binari. Pokok binari mungkin mempunyai beberapa segi tiga sama kaki. Kita perlu mencari jumlah bilangan segi tiga sama kaki yang mungkin dalam pokok binari ini.

Dalam artikel ini, kami akan meneroka beberapa teknik untuk menyelesaikan masalah ini dalam C++.

Memahami masalah

Memberi anda susunan induk. Anda perlu mewakilinya dalam bentuk pokok binari supaya indeks tatasusunan membentuk nilai nod pokok dan nilai dalam tatasusunan memberikan nod induk indeks tertentu itu.

Sila ambil perhatian bahawa -1 sentiasa menjadi nod induk akar. Diberikan di bawah adalah tatasusunan dan perwakilan pokok binarinya.

Parent array = [0, -1, 3, 1, 1, 2, 2, 3, 4, 4]

Pokok binari -

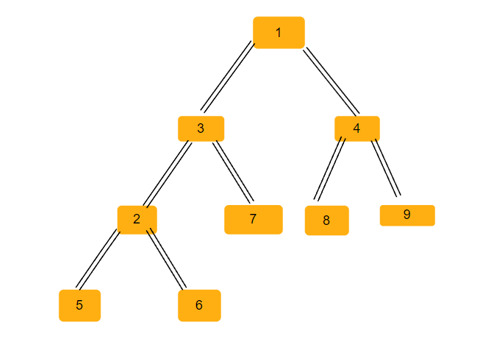
Dalam mana-mana pokok binari kita boleh mempunyai tiga jenis segi tiga sama kaki -

Segitiga Sama Kaki Kiri nod kanak-kanak. Nod anak boleh secara langsung atau tidak langsung. Dalam pokok di atas, kita mempunyai dua segi tiga sama kaki - (2, 6, 3), (3, 7, 1).

• . Kanak-kanak boleh secara langsung atau tidak langsung. Dalam pokok di atas, kita hanya mempunyai satu segi tiga sama kaki (4, 1, 8). Balanced Isosceles Triangle − Dalam segi tiga ini, bucu yang membentuk tapak ialah nod anak kiri dan kanan nod bucu. Dalam pokok di atas, kita mempunyai lima segi tiga sama kaki (1, 3, 4), (3, 2, 7), (4, 8, 9), (2, 5, 6), (1, 2, 9)

• Jadi, untuk pokok binari di atas, kami mempunyai sejumlah 8 segi tiga sama kaki. Perjalanan menggunakan carian depth-first Depth First Search (DFS) ialah kaedah merentasi semua nod pokok secara mendalam. Ia bermula pada nod akar, bergerak ke setiap cawangan, dan kemudian berundur. Pertama, kami menggunakan

  DFS
untuk merentasi setiap nod pokok binari dan menukarnya menjadi graf supaya setiap nod diwakili sebagai bersebelahan antara satu sama lain. Ini menjadikan perjalanan lebih mudah.

• Untuk setiap nod, kami menyemak sama ada ia mempunyai nod anak. Selepas menyemak, kami mengisihnya menggunakan fungsi sort(node[x].begin(), node[x].end()).

Seterusnya, kami menyemak sama ada nod semasa ialah pengganti kiri atau kanan nod induknya yang sepadan. Kami menggunakan fungsi DFS secara rekursif pada semua nod pokok binari.

Jika nod semasa mempunyai dua anak (langsung atau tidak langsung), kami menyemak kemungkinan segi tiga sama kaki wujud dengan mengira tepi di antara mereka. Kami akan mencari tepi di antara mereka melalui fungsi

graf

yang diberikan dalam kod di bawah.

Akhir sekali, kami mengira jumlah bilangan segi tiga sama kaki dengan menjumlahkan semua segi tiga yang mungkin dalam kedudukan yang berbeza.

• Contoh

  #include <iostream>
  #include <vector>
  #include <algorithm>
  #include <cstring>
  using namespace std;
  
  #define MAX int(1e5)
  vector < int > * node;
  int right_down[MAX];
  int right_up[MAX];
  int left_down[MAX];
  int left_up[MAX];
  
  // DFS traversal over a node
  void DFS(int x, int * parent) {
     // Check if adjacent nodes are present for node x
     if (node[x].size() != 0)
        sort(node[x].begin(), node[x].end());
  
     // Check whether the node has a parent node
     if (parent[x] != -1) {
        int indexOfParent = parent[x];
        int childrenCount = node[indexOfParent].size();
  
        if (childrenCount > 1) {
           int parentFirstChild = node[indexOfParent][0];
  
           // Check if current node is left node of the parent
           if (x == parentFirstChild) {
              right_up[x] += right_up[indexOfParent] + 1;
              // Check if current node is right node of the parent  
           } else {
              left_up[x] += left_up[indexOfParent] + 1;
           }
        } else {
           right_up[x] += right_up[indexOfParent] + 1;
        }
     }
  
     // Iterate over children of current node  
     for (int i = 0; i < node[x].size(); ++i) {
        int y = node[x][i];
        DFS(y, parent);
  
        // left child of current node
        if (i == 0) {
           left_down[x] += left_down[y] + 1;
        }
        // right child of current node
        else {
           right_down[x] += right_down[y] + 1;
        }
     }
  }
  
  int graph(int * parent, int N) {
     int rootNode;
     node = new vector < int > [N];
  
     for (int i = 0; i < N; ++i) {
        if (parent[i] != -1) {
           node[parent[i]].push_back(i);
        } else {
           rootNode = i;
        }
  
        left_up[i] = 0;
        right_up[i] = 0;
        left_down[i] = 0;
        right_down[i] = 0;
     }
     return rootNode;
  }
  
  int main() {
     int N = 10;
     int parent[] = { 0, -1, 3, 1, 1, 2, 2, 3, 4, 4 };
     int rootNode = graph(parent, N);
     DFS(rootNode, parent);
     int count = 0;
     // Counting the total isosceles triangles
     for (int i = 0; i < N; ++i) {
        count += min(right_down[i], right_up[i]);
        count += min(left_down[i], left_up[i]);
        count += min(left_down[i], right_down[i]);
     }
     cout << "Number of isosceles triangles in the binary tree are " <<
        count;
     return 0;
  }
  

  Output

  Number of isosceles triangles in the binary tree are 8
  

Kesimpulan

• Kami telah membincangkan cara mencari jumlah bilangan segi tiga sama sisi dalam pokok binari apabila diberikan tatasusunan induk. Kita boleh mencapai ini dengan menggunakan carian mendalam-pertama, yang membolehkan kita melintasi pokok binari.

Atas ialah kandungan terperinci Bilangan segi tiga sama kaki dalam pokok binari. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!