Tutorial melukis lengkok dan bulatan melalui HTML5 Canvas API_html5 petua tutorial

Dalam HTML5, objek CanvasRenderingContext2D juga menyediakan kaedah khusus untuk melukis bulatan atau lengkok Sila rujuk atribut dan pengenalan kaedah berikut:

Kod JavaScriptSalin kandungan ke papan keratan

1. arka(x, y, jejari, startRad, endRad, lawan jam)

Lukis lengkok pada bulatan dengan titik koordinat (x, y) sebagai pusat dan jejari sebagai jejari pada kanvas. Arka permulaan arka ini ialah startRad, dan arka penamat ialah endRad. Radian di sini dikira sebagai sudut putaran mengikut arah jam berdasarkan arah positif paksi-x (jam tiga pada jam). lawan arah jam menunjukkan sama ada hendak mula melukis mengikut arah lawan jam atau mengikut arah jam Jika benar, ia bermakna lawan jam, dan jika ia salah, ia bermakna mengikut arah jam. Parameter lawan jam adalah pilihan dan lalai kepada palsu, yang bermaksud mengikut arah jam.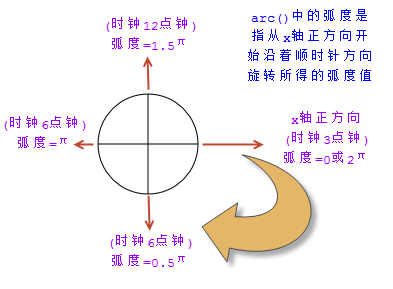

Kaedah pengiraan radian dalam kaedah arka()

Kod JavaScriptSalin kandungan ke papan keratan

1. arcTo(x1, y1, x2, y2, radius)

Kaedah ini akan menggunakan sudut yang dibentuk oleh titik akhir semasa, titik akhir 1 (x1, y1) dan titik akhir 2 (x2, y2), dan kemudian melukis bahagian yang bertangen kepada kedua-dua belah sudut dan mempunyai jejari jejari Lengkok pada bulatan. Secara umumnya, kedudukan permulaan melukis arka ialah titik akhir semasa, kedudukan penamat ialah titik akhir 2, dan arah melukis arka ialah arah arka terpendek yang menghubungkan dua titik akhir. Selain itu, jika titik akhir semasa tidak berada pada bulatan yang ditentukan, kaedah ini juga akan melukis garis lurus dari titik akhir semasa ke titik permulaan lengkok.
Memandangkan terdapat banyak ruang untuk memperkenalkan kaedah arcTo() secara terperinci, sila ke sini untuk melihat penggunaan terperinci arcTo().

Setelah memahami API di atas untuk melukis arka pada kanvas, mari kita lihat cara menggunakan arc() untuk melukis arka. Kita sudah tahu bahawa parameter ke-4 dan ke-5 yang diterima oleh arc() mewakili radian permulaan dan penamat lengkok. Saya percaya bahawa semua pembaca telah mempelajari tentang radian dalam matematik sekolah atau kursus geometri. Radian ialah unit sudut. Untuk lengkok yang panjang lengkoknya bersamaan dengan jejarinya, sudut pusat yang dicantumkannya ialah 1 radian. Kita juga tahu bahawa bulatan dengan jejari r mempunyai lilitan 2πr. Dengan pengetahuan geometri ini, kita boleh menggunakan kaedah arc() untuk melukis lengkok.

Gunakan kanvas untuk melukis arka

Sekarang, mari kita lukis 1/4 lengkok bulatan dengan jejari 50px.

Kod JavaScriptSalin kandungan ke papan keratan

3. "UTF-8">
6. "myCanvas"
7. lebar="400px"
8. tinggi="300px"
9. style="sempadan: 1px merah pepejal;"
10. > Pelayar anda tidak menyokong teg kanvas. "teks/javascript">
11. //Dapatkan objek Kanvas (kanvas)
13. var kanvas = document.getElementById(
14. "myCanvas"); //Cukup mengesan sama ada penyemak imbas semasa menyokong objek Canvas untuk mengelakkan ralat sintaks dalam sesetengah penyemak imbas yang tidak menyokong html5
15. jika
16. (canvas.getContext){  //Dapatkan objek CanvasRenderingContext2D (berus) yang sepadan
17.  var ctx = canvas.getContext("2d"
18. );   
19. //Mulakan laluan lukisan baharu ctx.beginPath();
20. //Tetapkan warna arka kepada biru ctx.strokeStyle =
21. "biru";
22. var bulatan = {
23. y : 100,
24. //Nilai koordinat paksi-Y pusat bulatan r : 50
25. //Jejari bulatan };
26. //Lukis lengkok mengikut arah jam bulatan dengan titik koordinat (100,100) sebagai pusat dan jejari 50px
27. ctx.arc(circle.x, circle.y, circle.r, 0, Math.PI / 2, false);
28. //Lukis lengkok mengikut laluan yang ditentukan
29. ctx.stroke(); }

31. Kesan paparan yang sepadan adalah seperti berikut:
    

    Gunakan kanvas untuk melukis lengkok mengikut arah jam
    Seperti yang ditunjukkan di atas, kami menetapkan koordinat tengah bulatan di mana lengkok yang dilukis terletak kepada (100,100) dan jejari kepada 50px. Oleh kerana lilitan bulatan dengan jejari r ialah 2πr, iaitu, radian sepadan bulatan lengkap ialah 2π (ditukar kepada sudut sekata ialah 360°), jadi kita ingin melukis 1/4 daripada Lengkok bulatan, selagi radian ialah π/2 (iaitu, 90°). Dalam kod di atas, kami menggunakan Math.PI tetap yang mewakili π dalam JavaScript.

    Selain itu, dalam kod di atas, kami juga menetapkan arah lukisan lengkok kepada arah jam (palsu). Oleh kerana radian permulaan ialah 0 dan radian berakhir ialah π/2, lengkok akan dilukis mengikut arah jam bermula dari arah positif paksi-x, menghasilkan graf di atas. Jika kita menukar arah lukisan arka dalam kod di atas kepada lawan jam, apakah kesannya?

    Kod JavaScriptSalin kandungan ke papan keratan

    1. "teks/javascript">
    2. //Dapatkan objek Kanvas (kanvas)
    3. var kanvas = document.getElementById("myCanvas"); //Cukup mengesan sama ada penyemak imbas semasa menyokong objek Canvas untuk mengelakkan ralat sintaks dalam sesetengah penyemak imbas yang tidak menyokong html5
    4. jika
    5. (canvas.getContext){  //Dapatkan objek CanvasRenderingContext2D (berus) yang sepadan
    6.  var
    7. ctx = canvas.getContext("2d");   
    8. //Mulakan laluan lukisan baharu
    9. ctx.beginPath();
    10. //Tetapkan warna arka kepada biru
    11. ctx.strokeStyle = "biru";
    12. var bulatan = {
    13. y : 100, //Nilai koordinat paksi-Y pusat bulatan
    14. r : 50 //Jejari bulatan
    15. };
    16. //Lukis lengkok mengikut arah lawan jam bulatan dengan titik koordinat (100,100) sebagai pusat dan jejari 50px ctx.arc(circle.x, circle.y, circle.r, 0, Math.PI / 2,
    17. true
    18. //Lukis lengkok mengikut laluan yang ditentukan
    19. ctx.stroke(); }

    20. Kesan paparan yang sepadan adalah seperti berikut:
        

        Gunakan kanvas untuk melukis lengkok mengikut arah lawan jam

        
        Gunakan kanvas untuk melukis bulatan

        Selepas kita belajar melukis lengkok, mudah untuk melukis bulatan dengan analogi Kita hanya perlu menukar lengkok pengakhiran kod di atas kepada 2π.

        Kod JavaScriptSalin kandungan ke papan keratan

        1. "teks/javascript">
        2. //Dapatkan objek Kanvas (kanvas)
        3. var kanvas = document.getElementById("myCanvas"); //Cukup mengesan sama ada penyemak imbas semasa menyokong objek Canvas untuk mengelakkan ralat sintaks dalam sesetengah penyemak imbas yang tidak menyokong html5
        4. jika
        5. (canvas.getContext){  //Dapatkan objek CanvasRenderingContext2D (berus) yang sepadan
        6.  var
        7. ctx = canvas.getContext("2d");   
        8. //Mulakan laluan lukisan baharu
        9. ctx.beginPath();
        10. //Tetapkan warna arka kepada biru
        11. ctx.strokeStyle = "biru";
        12. var bulatan = {
        13. y : 100, //Nilai koordinat paksi-Y pusat bulatan
        14. r : 50 //Jejari bulatan
        15. };
        16. //Dengan titik koordinat (100,100) dalam kanvas sebagai tengah, lukis bulatan dengan jejari 50px ctx.arc(circle.x, circle.y, circle.r, 0, Math.PI * 2,
        17. true
        18. //Lukis lengkok mengikut laluan yang ditentukan
        19. ctx.stroke(); }
        20. Kesan paparan yang sepadan adalah seperti berikut:
        22. Kod JavaScriptSalin kandungan ke papan keratan
        23. 3. Hinweis: Der Start-Radiant-Parameter startRad und der End-Radiant-Parameter endRad in der arc()-Methode sind beide im Bogenmaß angegeben. Auch wenn Sie eine Zahl wie 360 ​​eingeben, wird diese immer noch als 360 Bogenmaß betrachtet. Welche Konsequenzen hat es, wenn der Endbogen des obigen Codes auf 360 gesetzt wird? Dies hängt von der Zeichenrichtung ab (d. h. vom Wert des Parameters gegen den Uhrzeigersinn). Wenn er im Uhrzeigersinn gezeichnet wird (falsch), wird ein vollständiger Kreis gezeichnet, wenn er im Gegenuhrzeigersinn gezeichnet wird, werden Bogenmaße größer als 2π in a umgewandelt Bogenmaß gleich, aber nicht größer als 2π. Stellen Sie beispielsweise den Endbogen im obigen Code auf 3π (Math.PI * 3) ein. Wenn „gegen den Uhrzeigersinn“ falsch ist, wird er als vollständiger Kreis angezeigt. Wenn dies der Fall ist, ist der Anzeigeeffekt derselbe ist auf π gesetzt. Der Effekt ist konsistent.
            4. Wenn der Endbogen auf 3π eingestellt ist, wird der Zeicheneffekt einer (falschen) Drehung im Uhrzeigersinn erzielt

            Wenn der Endbogen auf 3π eingestellt ist, wird der Zeicheneffekt einer (echten) Drehung gegen den Uhrzeigersinn erzielt