Fahami dan satukan 14 algoritma atribusi untuk menjadikan rangkaian saraf boleh ditafsir

Walaupun DNN telah mencapai kejayaan yang meluas dalam pelbagai aplikasi praktikal, proses mereka sering dianggap sebagai kotak hitam kerana sukar untuk menerangkan cara DNN membuat keputusan. Kekurangan kebolehtafsiran menjejaskan kebolehpercayaan DNN, sekali gus menghalang penggunaannya yang meluas dalam tugasan berisiko tinggi seperti pemanduan autonomi dan perubatan AI. Oleh itu, DNN yang boleh dijelaskan telah menarik perhatian yang semakin meningkat.

Sebagai perspektif tipikal untuk menerangkan DNN, kaedah atribusi bertujuan untuk mengira skor atribusi/kepentingan/sumbangan setiap pembolehubah input kepada output rangkaian. Contohnya, memandangkan DNN terlatih untuk klasifikasi imej dan imej input, skor atribut untuk setiap pembolehubah input merujuk kepada kesan berangka setiap piksel pada skor keyakinan klasifikasi.

Walaupun penyelidik telah mencadangkan banyak kaedah atribusi dalam beberapa tahun kebelakangan ini, kebanyakannya adalah berdasarkan heuristik yang berbeza. Pada masa ini terdapat kekurangan perspektif teori yang bersatu untuk menguji ketepatan kaedah atribusi ini, atau sekurang-kurangnya untuk menjelaskan secara matematik mekanisme terasnya.

Penyelidik telah cuba menyatukan kaedah atribusi yang berbeza, tetapi kajian ini hanya merangkumi beberapa kaedah.

Dalam artikel ini, kami mencadangkan "penjelasan bersatu tentang mekanisme intrinsik 14 algoritma atribusi kepentingan unit input."

Alamat kertas: https://arxiv.org/pdf/2303.01506.pdf

Malah, sama ada "12 algoritma untuk meningkatkan ketahanan terhadap penghijrahan" atau "14 algoritma atribusi kepentingan unit input", semuanya paling teruk terjejas oleh algoritma kejuruteraan. Dalam kedua-dua bidang ini, kebanyakan algoritma adalah empirikal. Orang mereka bentuk beberapa algoritma kejuruteraan yang munasabah berdasarkan pengalaman percubaan atau pemahaman intuitif. Kebanyakan kajian tidak membuat definisi yang ketat dan demonstrasi teori tentang "apa sebenarnya kepentingan unit input". Sudah tentu, masalah "kekurangan definisi dan demonstrasi yang ketat" merangkumi seluruh bidang kecerdasan buatan, tetapi amat menonjol dalam kedua-dua arah ini.

• Pertama, dalam persekitaran di mana banyak algoritma atribusi empirikal membanjiri bidang pembelajaran mesin boleh tafsir, kami berharap dapat membuktikan bahawa "semua 14 algoritma atribusi (mentafsir input rangkaian saraf mekanisme algoritma kepentingan unit boleh dinyatakan sebagai pengedaran utiliti interaksi yang dimodelkan oleh rangkaian saraf, dan algoritma atribusi yang berbeza sepadan dengan perkadaran pengedaran utiliti interaksi yang berbeza." Dengan cara ini, walaupun algoritma yang berbeza mempunyai fokus reka bentuk yang berbeza sama sekali (contohnya, sesetengah algoritma mempunyai fungsi objektif yang digariskan, dan sesetengah algoritma adalah saluran paip tulen), kami mendapati bahawa secara matematik, algoritma ini boleh dimasukkan dalam pengedaran "utiliti interaksi" " " logik naratif.
• Berdasarkan rangka kerja peruntukan utiliti interaktif di atas, kami seterusnya boleh mencadangkan tiga kriteria penilaian untuk algoritma atribusi kepentingan unit input rangkaian saraf untuk mengukur kepentingan unit input yang diramalkan oleh algoritma atribusi Adakah nilai yang munasabah?

Sudah tentu, analisis teori kami bukan sahaja terpakai pada 14 algoritma atribusi, dan secara teori boleh menyatukan lebih banyak penyelidikan yang serupa. Oleh kerana tenaga kerja yang terhad, kami hanya membincangkan 14 algoritma dalam kertas ini.

Kesukaran sebenar dalam penyelidikan ialah algoritma atribusi empirikal yang berbeza selalunya dibina berdasarkan gerak hati yang berbeza dan setiap kertas hanya berusaha untuk "membenarkan dirinya sendiri" dari perspektifnya sendiri, setiap algoritma atribusi reka bentuk berdasarkan intuisi atau perspektif yang berbeza, tetapi tidak mempunyai bahasa matematik yang seragam untuk menerangkan secara seragam intipati pelbagai algoritma.

Semakan Algoritma

Sebelum bercakap tentang matematik, artikel ini akan menyemak secara ringkas algoritma sebelumnya dari tahap intuitif.

1. Algoritma atribusi berasaskan kecerunan. Algoritma jenis ini secara amnya percaya bahawa kecerunan output rangkaian saraf kepada setiap unit input boleh mencerminkan kepentingan unit input. Sebagai contoh, algoritma Gradien*Input memodelkan kepentingan unit input sebagai hasil keluaran kecerunan unsur dan nilai unit input. Memandangkan kecerunan hanya boleh mencerminkan kepentingan setempat bagi unit input, algoritma Kecerunan Licin dan Kecerunan Bersepadu memodelkan kepentingan sebagai hasil darab unsur kecerunan purata dan nilai unit input, di mana kecerunan purata dalam kedua-dua kaedah ini merujuk kepada jiran sampel input masing-masing Nilai purata kecerunan dalam domain atau kecerunan purata titik interpolasi linear antara sampel input dan titik garis dasar. Begitu juga, algoritma Grad-CAM mengambil purata keluaran rangkaian ke atas semua kecerunan ciri dalam setiap saluran untuk mengira skor kepentingan. Tambahan pula, algoritma Kecerunan Jangkaan percaya bahawa memilih satu titik penanda aras selalunya akan membawa kepada hasil atribusi berat sebelah, dengan itu mencadangkan untuk memodelkan kepentingan sebagai jangkaan hasil atribusi Kecerunan Bersepadu di bawah titik penanda aras yang berbeza.

2. Algoritma Atribusi berdasarkan perambatan balik lapisan demi lapisan. Rangkaian saraf dalam selalunya sangat kompleks, dan struktur setiap lapisan rangkaian saraf adalah agak mudah (contohnya, ciri dalam biasanya merupakan jumlah linear bagi ciri cetek + fungsi pengaktifan bukan linear), yang memudahkan analisis kepentingan ciri cetek kepada ciri yang mendalam. Oleh itu, jenis algoritma ini memperoleh kepentingan unit input dengan menganggar kepentingan ciri peringkat pertengahan dan menyebarkan kepentingan ini lapisan demi lapisan sehingga lapisan input. Algoritma dalam kategori ini termasuk LRP-epsilon, LRP-alphabeta, Deep Taylor, DeepLIFT Rescale, DeepLIFT RevealCancel, DeepShap, dsb. Perbezaan asas antara algoritma perambatan belakang yang berbeza ialah mereka menggunakan peraturan perambatan kepentingan yang berbeza lapisan demi lapisan.

3. Algoritma jenis ini menyimpulkan kepentingan unit input berdasarkan kesan penutupan unit input pada output model. Sebagai contoh, algoritma Occlusion-1 (Occlusion-patch) memodelkan kepentingan piksel ke-i (blok piksel) sebagai perubahan dalam output apabila piksel i tidak terhalang dan terhalang apabila piksel lain tidak terhalang. Algoritma nilai Shapley secara menyeluruh mempertimbangkan semua kemungkinan situasi oklusi bagi piksel lain dan memodelkan kepentingan kerana purata perubahan output sepadan dengan piksel i di bawah situasi oklusi yang berbeza. Penyelidikan telah membuktikan bahawa nilai Shapley ialah satu-satunya algoritma atribusi yang memenuhi aksiom lineariti, dummy, simetri dan kecekapan.

Menyatukan mekanisme dalaman 14 algoritma atribusi empirikal

Selepas kajian mendalam tentang pelbagai algoritma atribusi empirikal, kami tidak boleh tidak memikirkan soalan: di tahap matematik Apakah masalah atribusi penyelesaian rangkaian saraf? Adakah terdapat beberapa pemodelan dan paradigma matematik bersatu di sebalik banyak algoritma atribusi empirikal? Untuk tujuan ini, kami cuba mempertimbangkan isu di atas bermula daripada definisi atribusi. Atribusi merujuk kepada skor kepentingan/sumbangan setiap unit input kepada output rangkaian saraf. Kemudian, kunci untuk menyelesaikan masalah di atas adalah untuk (1) memodelkan "mekanisme pengaruh unit input pada output rangkaian" pada tahap matematik dan (2) menerangkan berapa banyak algoritma atribusi empirikal menggunakan mekanisme pengaruh ini untuk mereka bentuk kepentingan. Formula atribusi.

Mengenai perkara utama pertama, penyelidikan kami mendapati bahawa setiap unit input sering mempengaruhi output rangkaian saraf dalam dua cara. Di satu pihak, unit input tertentu tidak perlu bergantung pada unit input lain dan boleh bertindak secara bebas dan mempengaruhi output rangkaian ini dipanggil "kesan bebas". Sebaliknya, unit input perlu bekerjasama dengan unit input lain untuk membentuk corak tertentu, dengan itu mempengaruhi output rangkaian ini dipanggil "kesan interaksi". Teori kami membuktikan bahawa output rangkaian saraf boleh didekonstruksi secara ketat kepada kesan bebas pembolehubah input yang berbeza, serta kesan interaktif antara pembolehubah input dalam set yang berbeza.

Antaranya, mewakili kesan bebas unit input ke-i, dan mewakili kesan berbilang dalam set S Kesan interaksi antara unit input. Mengenai perkara utama kedua, kami mendapati bahawa mekanisme dalaman semua 14 algoritma atribusi empirikal sedia ada boleh mewakili peruntukan utiliti bebas dan utiliti interaktif di atas, dan atribusi berbeza Algoritma mengedarkan utiliti bebas dan utiliti interaktif. daripada unit input rangkaian saraf dalam perkadaran yang berbeza. Khususnya, biarkan ​ mewakili skor atribusi unit input ke-i. Kami membuktikan dengan teliti bahawa yang diperolehi oleh kesemua 14 algoritma atribusi empirikal boleh dinyatakan secara seragam sebagai paradigma matematik berikut (iaitu, jumlah wajaran utiliti bebas dan utiliti interaktif): ​ ​ di mana, menggambarkan perkadaran memberikan kesan bebas unit input ke-j kepada unit input ke-i, Mewakili perkadaran kesan interaksi antara berbilang unit input dalam set S yang diberikan kepada unit input ke-i. "Perbezaan asas" antara banyak algoritma atribusi ialah algoritma atribusi yang berbeza sepadan dengan nisbah peruntukan yang berbeza .

Jadual 1 menunjukkan cara empat belas algoritma atribusi berbeza memperuntukkan kesan bebas dan kesan interaktif. Carta 1. Empat belas algoritma atribusi boleh ditulis sebagai kesan bebas dan kesan interaktif Paradigma matematik untuk jumlah wajaran. Antaranya,

mewakili kesan bebas Taylor dan kesan interaksi Taylor masing-masing, memuaskan

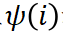ialah penghalusan kesan bebas dan kesan interaktif .

Tiga kriteria utama untuk menilai kebolehpercayaan algoritma atribusi

Dalam penyelidikan penjelasan atribusi, memandangkan tiada cara untuk mendapatkan/melabelkan nilai sebenar penjelasan atribusi rangkaian saraf, orang tidak boleh menilai kebolehpercayaan algoritma penjelasan atribusi tertentu daripada perspektif empirikal. Kelemahan asas "kekurangan kriteria penilaian objektif untuk kebolehpercayaan algoritma penjelasan atribusi" telah mencetuskan kritikan dan persoalan yang meluas dalam bidang akademik penyelidikan penjelasan atribusi.

Pendedahan mekanisme awam algoritma atribusi dalam kajian ini membolehkan kami menilai dan membandingkan dengan adil kebolehpercayaan algoritma atribusi yang berbeza di bawah rangka kerja teori yang sama. Secara khusus, kami mencadangkan tiga kriteria penilaian berikut untuk menilai sama ada algoritma atribusi tertentu mengedarkan kesan bebas dan kesan interaktif secara adil dan munasabah.

(1) Garis Panduan 1: Merangkumi semua kesan bebas dan kesan interaktif dalam proses peruntukan. Selepas kami menyahbina keluaran rangkaian saraf kepada kesan bebas dan kesan interaktif, algoritma atribusi yang boleh dipercayai harus meliputi semua kesan bebas dan kesan interaktif sebanyak mungkin dalam proses peruntukan. Sebagai contoh, atribusi kepada ayat Saya tidak gembira harus meliputi semua kesan bebas daripada tiga perkataan saya, tidak, gembira, dan juga meliputi J (saya, tidak), J (saya, gembira ), J (tidak, gembira), J (Saya, tidak, gembira), dsb. semua kemungkinan kesan interaksi.

(2) Garis Panduan 2: Elakkan memberikan kesan bebas dan interaksi kepada unit input yang tidak berkaitan . Kesan bebas unit input ke-i hanya harus diberikan kepada unit input ke-i dan bukan kepada unit input lain. Begitu juga, kesan interaksi antara unit input dalam set S hanya harus diberikan kepada unit input dalam set S dan bukan kepada unit input di luar set S (tidak mengambil bahagian dalam interaksi). Sebagai contoh, kesan interaksi antara tidak dan gembira tidak boleh diberikan kepada perkataan saya.

(3) Garis Panduan 3: Pengedaran lengkap . Setiap kesan bebas (kesan interaksi) hendaklah diberikan sepenuhnya kepada unit input yang sepadan. Dalam erti kata lain, nilai atribusi yang diperuntukkan kepada semua unit input yang sepadan dengan kesan bebas tertentu (kesan interaksi) harus menambah sehingga tepat nilai kesan bebas (kesan interaksi). Sebagai contoh, kesan interaksi J (tidak, gembira) akan menetapkan sebahagian daripada kesan (tidak, gembira) kepada perkataan tidak, dan juga menetapkan sebahagian daripada kesan (tidak, gembira) Berikan perkataan gembira. Kemudian, nisbah pengagihan harus memenuhi .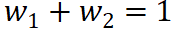

Seterusnya, kami menggunakan tiga kriteria penilaian ini untuk menilai 14 algoritma atribusi berbeza di atas (seperti ditunjukkan dalam Jadual 2). Kami mendapati bahawa algoritma Kecerunan Bersepadu, Kecerunan Jangkaan, nilai Shapley, Deep Shap, DeepLIFT Rescale dan DeepLIFT RevealCancel memenuhi semua kriteria kebolehpercayaan.

Jadual 2. Ringkasan sama ada 14 algoritma atribusi yang berbeza memenuhi ketiga-tiga kebolehpercayaan kriteria penilaian kriteria.

Pengenalan kepada pengarang

Pengarang artikel ini, Deng Huiqi, adalah Ph.D dalam matematik gunaan dari Universiti Sun Yat-sen. Semasa Ph.D., beliau bekerja di Jabatan Sains Komputer di Hong Kong Baptist University dan pelajar Texas A&M University Visiting, kini menjalankan penyelidikan pasca doktoral dalam pasukan Zhang Quanshi. Arah penyelidikan terutamanya adalah pembelajaran mesin yang boleh dipercayai/boleh ditafsir, termasuk menerangkan kepentingan atribusi rangkaian saraf dalam, menerangkan keupayaan ekspresif rangkaian saraf, dsb.

Deng Huiqi melakukan banyak kerja pada peringkat awal. Cikgu Zhang hanya membantunya menyusun semula teori selepas kerja awal selesai untuk menjadikan kaedah pembuktian dan sistem lebih lancar. Deng Huiqi tidak menulis banyak kertas kerja sebelum tamat pengajian Selepas datang ke Teacher Zhang pada penghujung tahun 2021, dia melakukan tiga tugas dalam lebih setahun di bawah sistem interaksi permainan, termasuk (1) menemui dan secara teori menjelaskan kesesakan representasi biasa saraf. rangkaian, iaitu, rangkaian Neural telah terbukti kurang mahir dalam memodelkan perwakilan interaktif dengan kerumitan sederhana. Kerja ini cukup bernasib baik kerana dipilih sebagai kertas lisan ICLR 2022, dan skor ulasannya berada dalam lima teratas (skor 8 8 8 10). (2) Teori ini membuktikan trend perwakilan konsep rangkaian Bayesian dan menyediakan perspektif baharu untuk menerangkan prestasi klasifikasi, keupayaan generalisasi dan keteguhan lawan bagi rangkaian Bayesian. (3) Secara teorinya menerangkan keupayaan rangkaian saraf untuk mempelajari konsep interaktif kerumitan yang berbeza semasa proses latihan.

Atas ialah kandungan terperinci Fahami dan satukan 14 algoritma atribusi untuk menjadikan rangkaian saraf boleh ditafsir. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!