Rumah >pembangunan bahagian belakang >Tutorial Python >Fungsi kehilangan yang biasa digunakan dan contoh pelaksanaan Python
Fungsi kehilangan yang biasa digunakan dan contoh pelaksanaan Python
- 王林ke hadapan
- 2023-04-26 13:40:071740semak imbas
Apakah fungsi kehilangan?
Fungsi kehilangan ialah algoritma yang mengukur sejauh mana model sesuai dengan data. Fungsi kerugian ialah satu cara untuk mengukur perbezaan antara ukuran sebenar dan nilai ramalan. Semakin tinggi nilai fungsi kerugian, semakin tidak tepat ramalannya, dan semakin rendah nilai fungsi kerugian, semakin dekat ramalan dengan nilai sebenar. Fungsi kehilangan dikira untuk setiap pemerhatian individu (titik data). Fungsi yang meratakan nilai semua fungsi kerugian dipanggil fungsi kos Pemahaman yang lebih mudah ialah fungsi kehilangan adalah untuk satu sampel, manakala fungsi kos adalah untuk semua sampel.
Fungsi dan metrik kerugian
Sesetengah fungsi kehilangan juga boleh digunakan sebagai metrik penilaian. Tetapi fungsi dan metrik kerugian mempunyai tujuan yang berbeza. Walaupun metrik digunakan untuk menilai model akhir dan membandingkan prestasi model yang berbeza, fungsi kehilangan digunakan semasa fasa pembinaan model sebagai pengoptimum untuk model yang dibuat. Fungsi kehilangan membimbing model tentang cara meminimumkan ralat.
Dalam erti kata lain, fungsi kehilangan mengetahui cara model dilatih, dan indeks pengukuran menerangkan prestasi model
Mengapa menggunakan fungsi kehilangan?
Kerana ukuran fungsi kehilangan ialah perbezaan antara nilai ramalan dan nilai sebenar, jadi ia boleh digunakan untuk membimbing penambahbaikan model semasa melatih model (kaedah turunan kecerunan biasa). Dalam proses membina model, jika berat ciri berubah dan mendapat ramalan yang lebih baik atau lebih buruk, adalah perlu untuk menggunakan fungsi kehilangan untuk menilai sama ada berat ciri dalam model perlu diubah, dan arah berubah.
Kami boleh menggunakan pelbagai fungsi kehilangan dalam pembelajaran mesin, bergantung pada jenis masalah yang kami cuba selesaikan, kualiti data dan pengedaran, dan algoritma yang kami gunakan. Rajah berikut menunjukkan 10 yang kami ada disusun fungsi kehilangan biasa:
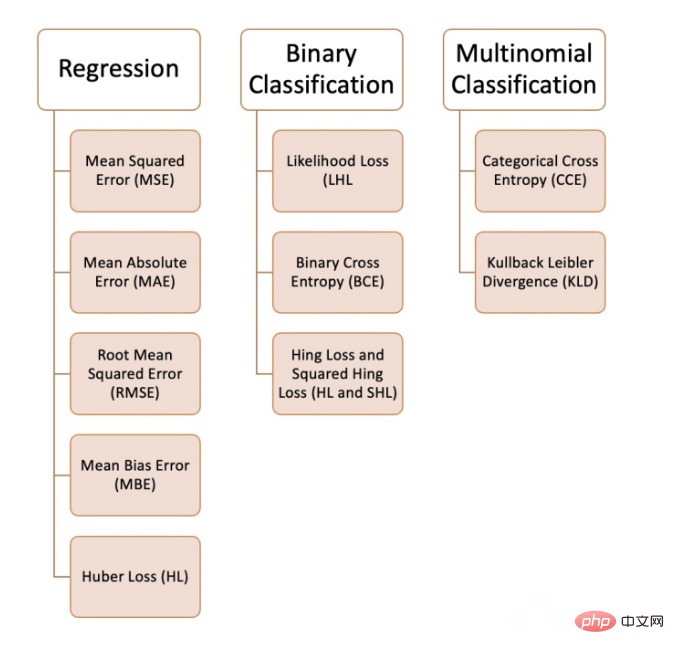
Masalah regresi
1. Ralat min kuasa dua (MSE)
Ralat kuasa dua min merujuk kepada semua nilai yang diramalkan. dan nilai sebenar, dan purata mereka. Selalunya digunakan dalam masalah regresi.
def MSE (y, y_predicted): sq_error = (y_predicted - y) ** 2 sum_sq_error = np.sum(sq_error) mse = sum_sq_error/y.size return mse
2. Min ralat mutlak (MAE)
dikira sebagai purata perbezaan mutlak antara nilai ramalan dan nilai sebenar. Ini adalah ukuran yang lebih baik daripada ralat kuasa dua min apabila data mempunyai outlier.
def MAE (y, y_predicted): error = y_predicted - y absolute_error = np.absolute(error) total_absolute_error = np.sum(absolute_error) mae = total_absolute_error/y.size return mae
3. Ralat min kuasa dua akar (RMSE)
Fungsi kehilangan ini ialah punca kuasa dua ralat min kuasa dua. Ini adalah pendekatan yang ideal jika kita tidak mahu menghukum kesilapan yang lebih besar.
def RMSE (y, y_predicted): sq_error = (y_predicted - y) ** 2 total_sq_error = np.sum(sq_error) mse = total_sq_error/y.size rmse = math.sqrt(mse) return rmse
4. Min Ralat Bias (MBE)
adalah serupa dengan min ralat mutlak tetapi tidak mengira nilai mutlak. Kelemahan fungsi kehilangan ini ialah ralat negatif dan positif boleh membatalkan satu sama lain, jadi adalah lebih baik untuk mengaplikasikannya apabila pengkaji tahu bahawa ralat hanya pergi ke satu arah.
def MBE (y, y_predicted): error = y_predicted -y total_error = np.sum(error) mbe = total_error/y.size return mbe
5. Kehilangan Huber
Fungsi kerugian Huber menggabungkan kelebihan ralat mutlak min (MAE) dan ralat kuasa dua min (MSE). Ini kerana Hubber loss adalah fungsi dengan dua cawangan. Satu cabang digunakan pada MAE yang sepadan dengan nilai yang dijangkakan, dan cabang lain digunakan pada outlier. Fungsi umum Hubber Loss ialah:
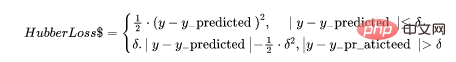
Di sini
def hubber_loss (y, y_predicted, delta) delta = 1.35 * MAE y_size = y.size total_error = 0 for i in range (y_size): erro = np.absolute(y_predicted[i] - y[i]) if error < delta: hubber_error = (error * error) / 2 else: hubber_error = (delta * error) / (0.5 * (delta * delta)) total_error += hubber_error total_hubber_error = total_error/y.size return total_hubber_error
Pengkelasan binari
6. Kehilangan kemungkinan maksimum (Likelihood Loss/LHL)
Fungsi kehilangan ini digunakan terutamanya untuk masalah klasifikasi binari. Kebarangkalian setiap nilai yang diramalkan didarabkan untuk mendapatkan nilai kerugian, dan fungsi kos yang berkaitan ialah purata semua nilai yang diperhatikan. Mari kita ambil contoh klasifikasi binari berikut di mana kelasnya ialah [0] atau [1]. Jika kebarangkalian keluaran adalah sama dengan atau lebih besar daripada 0.5, kelas yang diramalkan ialah [1], sebaliknya ia adalah [0]. Contoh kebarangkalian keluaran adalah seperti berikut:
[0.3 , 0.7 , 0.8 , 0.5 , 0.6 , 0.4]
Kelas ramalan yang sepadan ialah:
[0 , 1 , 1 , 1 , 1 , 0]
Dan kelas sebenar ialah:
[0 , 1 , 1 , 0 , 1 , 0]
Sekarang yang sebenar akan digunakan kelas dan kebarangkalian keluaran untuk mengira kerugian. Jika kelas sebenar ialah [1], kami menggunakan kebarangkalian keluaran, jika kelas sebenar ialah [0], kami menggunakan kebarangkalian 1:
((1–0.3)+0.7+0.8+(1–0.5)+0.6+(1–0.4)) / 6 = 0.65
Kod Python adalah seperti berikut:
def LHL (y, y_predicted): likelihood_loss = (y * y_predicted) + ((1-y) * (y_predicted)) total_likelihood_loss = np.sum(likelihood_loss) lhl = - total_likelihood_loss / y.size return lhl
7 , Binary Cross Entropy (BCE)
Fungsi ini ialah pengubahsuaian kehilangan kemungkinan logaritma. Susunan nombor boleh menghukum ramalan yang sangat yakin tetapi salah. Formula umum untuk fungsi kehilangan entropi silang binari ialah:
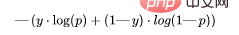
Mari kita teruskan menggunakan nilai dari contoh di atas:
- Kebarangkalian output = [0.3, 0.7, 0.8, 0.5, 0.6, 0.4]
- Kelas sebenar = [0, 1, 1, 0, 1, 0]
- (0 . log (0.3) + (1–0) . log (1–0.3)) = 0.155
- (1 . log(0.7) + (1–1) . log ( 0.3)) = 0.155
- (1 . log(0.8) + (1–1) . log (0.2)) = 0.097
- (0 . log (0.5) + (1–0 ) . log ( 1–0.5)) = 0.301
- (1 . log(0.6) + (1–1) . log (0.4)) = 0.222
- (0 . log (0.4 ) + (1 –0) . log (1–0.4)) = 0.222
Kemudian hasil daripada fungsi kos ialah:
(0.155 + 0.155 + 0.097 + 0.301 + 0.222 + 0.222) / 6 = 0.192
Kod Python adalah seperti berikut :
def BCE (y, y_predicted): ce_loss = y*(np.log(y_predicted))+(1-y)*(np.log(1-y_predicted)) total_ce = np.sum(ce_loss) bce = - total_ce/y.size return bce
8. Kehilangan Engsel dan Kehilangan Engsel Kuasa Dua (HL dan SHL)
Kehilangan Engsel diterjemahkan sebagai Kehilangan Engsel atau Kehilangan Engsel akan diguna pakai di sini.
Hinge Loss主要用于支持向量机模型的评估。错误的预测和不太自信的正确预测都会受到惩罚。所以一般损失函数是:
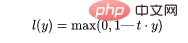
这里的t是真实结果用[1]或[-1]表示。
使用Hinge Loss的类应该是[1]或-1。为了在Hinge loss函数中不被惩罚,一个观测不仅需要正确分类而且到超平面的距离应该大于margin(一个自信的正确预测)。如果我们想进一步惩罚更高的误差,我们可以用与MSE类似的方法平方Hinge损失,也就是Squared Hinge Loss。
如果你对SVM比较熟悉,应该还记得在SVM中,超平面的边缘(margin)越高,则某一预测就越有信心。如果这块不熟悉,则看看这个可视化的例子:
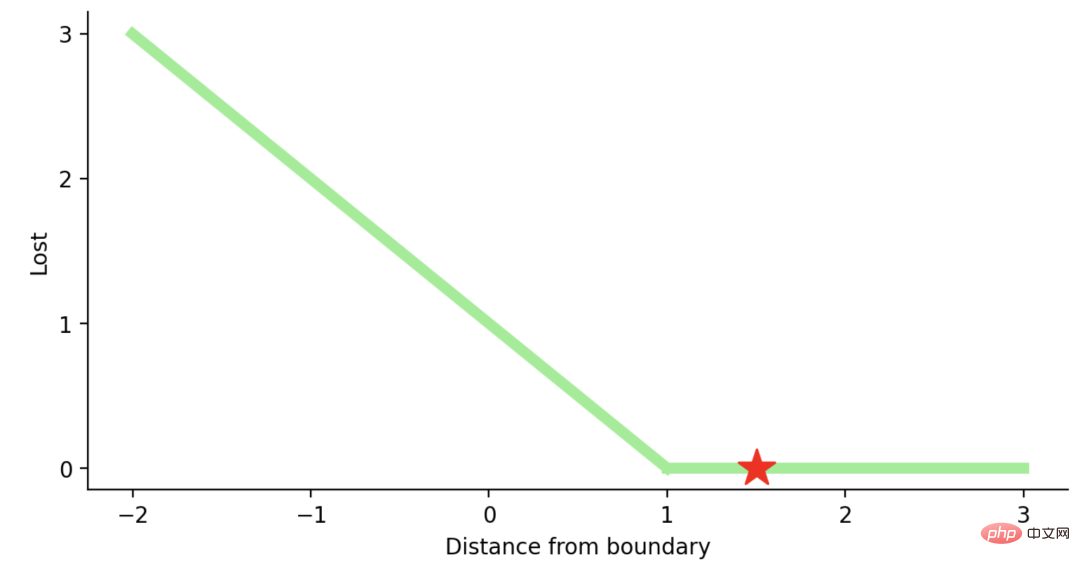
如果一个预测的结果是1.5,并且真正的类是[1],损失将是0(零),因为模型是高度自信的。
loss= Max (0,1 - 1* 1.5) = Max (0, -0.5) = 0
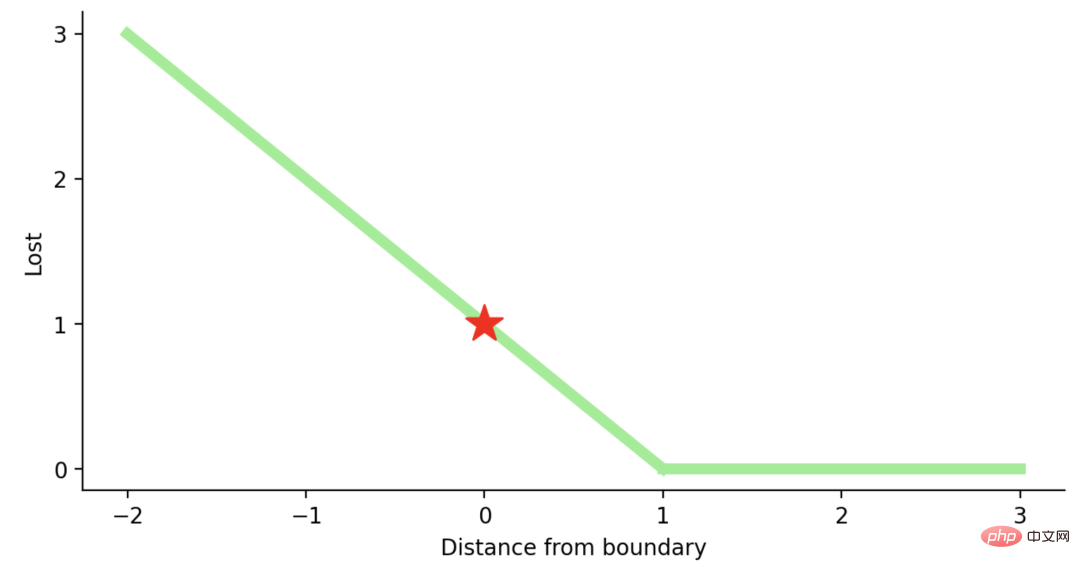
如果一个观测结果为0(0),则表示该观测处于边界(超平面),真实的类为[-1]。损失为1,模型既不正确也不错误,可信度很低。
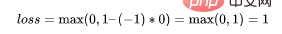
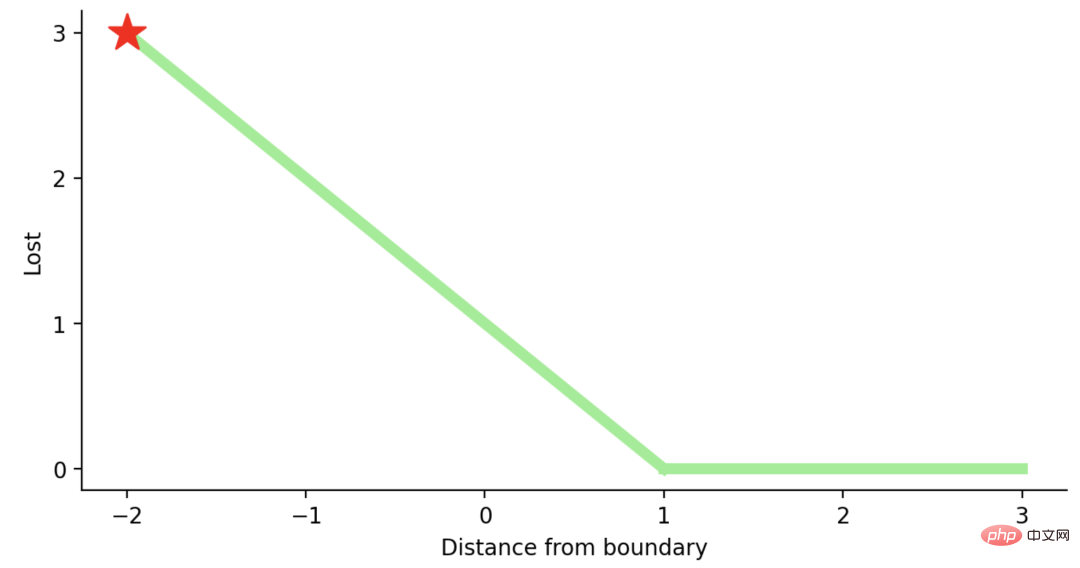
如果一次观测结果为2,但分类错误(乘以[-1]),则距离为-2。损失是3(非常高),因为我们的模型对错误的决策非常有信心(这个是绝不能容忍的)。
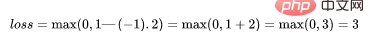
python代码如下:
#Hinge Loss def Hinge (y, y_predicted): hinge_loss = np.sum(max(0 , 1 - (y_predicted * y))) return hinge_loss #Squared Hinge Loss def SqHinge (y, y_predicted): sq_hinge_loss = max (0 , 1 - (y_predicted * y)) ** 2 total_sq_hinge_loss = np.sum(sq_hinge_loss) return total_sq_hinge_loss
多分类
9、交叉熵(CE)
在多分类中,我们使用与二元交叉熵类似的公式,但有一个额外的步骤。首先需要计算每一对[y, y_predicted]的损失,一般公式为:
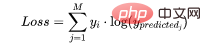
如果我们有三个类,其中单个[y, y_predicted]对的输出是:

这里实际的类3(也就是值=1的部分),我们的模型对真正的类是3的信任度是0.7。计算这损失如下:
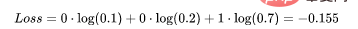
为了得到代价函数的值,我们需要计算所有单个配对的损失,然后将它们相加最后乘以[-1/样本数量]。代价函数由下式给出:
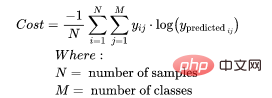
使用上面的例子,如果我们的第二对:

那么成本函数计算如下:
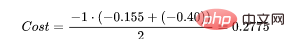
使用Python的代码示例可以更容易理解;
def CCE (y, y_predicted): cce_class = y * (np.log(y_predicted)) sum_totalpair_cce = np.sum(cce_class) cce = - sum_totalpair_cce / y.size return cce
10、Kullback-Leibler 散度 (KLD)
又被简化称为KL散度,它类似于分类交叉熵,但考虑了观测值发生的概率。如果我们的类不平衡,它特别有用。
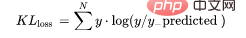
def KL (y, y_predicted): kl = y * (np.log(y / y_predicted)) total_kl = np.sum(kl) return total_kl
以上就是常见的10个损失函数,希望对你有所帮助。
Atas ialah kandungan terperinci Fungsi kehilangan yang biasa digunakan dan contoh pelaksanaan Python. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!

