Apakah kaedah untuk melaksanakan fungsi ajaib dan simulasi pengkomputeran kuantum dalam Python?

Latar belakang simulasi pengkomputeran kuantum

ProjectQ ialah rangka kerja pengaturcaraan kuantum sumber terbuka yang sangat elegan Pengarang asalnya ialah Dr. Damian dari Institut Persekutuan Switzerland Teknologi dan Thomas. Rangka kerja pengaturcaraan pengkomputeran kuantum ini ialah rangka kerja pengaturcaraan pengkomputeran kuantum yang sangat komprehensif yang dilaksanakan daripada aplikasi pengkomputeran kuantum ->penyusunan litar kuantum ->simulasi Hamiltonian ->simulasi pengkomputeran kuantum ->dok API perkakasan kuantum. Menyokong pemasangan menggunakan pip: python3 -m pip install projectq --upgrade.

Mari kita lihat contoh cara menggunakan projectq untuk mensimulasikan pengkomputeran kuantum:

[dechin@dechin-manjaro simulator]$ ipython
Python 3.8.5 (default, Sep  4 2020, 07:30:14) 
Type 'copyright', 'credits' or 'license' for more information
IPython 7.19.0 -- An enhanced Interactive Python. Type '?' for help.
 
In [1]: from projectq import MainEngine
 
In [2]: from projectq.ops import X
 
In [3]: eng = MainEngine()
 
In [4]: qubits = eng.allocate_qureg(2)
 
In [5]: X | qubits[0]
 
In [6]: from projectq.ops import CX
 
In [7]: CX | (qubits[0], qubits[1])
 
In [8]: eng.flush()
 
In [9]: print (eng.backend.cheat()[1])
[0j, 0j, 0j, (1+0j)]

Dalam kes ini, kami memperuntukkan sejumlah 2 qubit. Keadaan awal adalah semua |0〉 keadaan, dan vektor amplitud yang sepadan dengan output projectq hendaklah [1, 0, 0, 0]. Empat elemen dalam vektor ini sepadan dengan amplitud kebarangkalian bagi empat keadaan kuantum masing-masing 00, 01, 10, dan 11 Jika anda perlu mengira kebarangkalian keadaan tertentu diukur, anda perlu melakukan operasi kuasa dua modulo padanya . :

P(00)=(a₀₀+b₀₀i)(a₀₀&tolak;b₀₀i)

Perhatikan bahawa amplitud kebarangkalian ialah nombor kompleks, jadi adalah perlu untuk mengambil konjugat Hermitian dan kemudian melakukan operasi pendaraban titik.

Jadi kembali kepada kes penggunaan projectq di atas, selepas memperuntukkan dua bit, operasi matriks Pauli σ^X dilakukan pada bit pertama, dan kemudian Gerbang kekusutan. operasi CX dilakukan. Di sini, operasi yang sepadan dengan operasi get kuantum CX(i,j) ialah: jika qubit i berada dalam keadaan |0〉 diambil. Operasi songsang, iaitu, jika j asal ialah |0〉, ia akan menjadi |1〉, jika j asal ialah |1〉, ia akan menjadi |0〉. Ini ialah peranan kuantum kuantum dalam pengkomputeran kuantum, dan pelaksanaan berkualiti tinggi bagi operasi get berbilang bit dalam sistem perkakasan sebenar masih menjadi masalah besar. Ciri superposisi kuantum dicerminkan bahawa qubit mungkin berada dalam keadaan |0〉 atau ia mungkin berada dalam keadaan pertengahan antara |0〉 akan menjadi seperti yang dinyatakan di atas untuk membahagikan |0〉 dan |1〉 >i)&sdot ;(a

0

&tolak;b₀i)P(1)=(a₁+b₁i)⋅(a

1

&tolak;b₁i)Amplitud kebarangkalian ini boleh disusun dalam bentuk vektor: |ψ〉=(a₀+b

0

i,a

1

+b₁i) _TAkhirnya, bilangan elemen dalam vektor ini akan meningkat secara eksponen apabila bilangan bit bertambah Apabila bilangan bit meningkat kepada 41, ruang memori yang diperlukan untuk menyimpannya akan memerlukan lebih daripada 32TB! Perlu diingat bahawa kerana semua amplitud kebarangkalian perlu dimuatkan ke dalam memori semasa proses pengiraan, ini berbeza daripada ruang storan cakera keras Memori sahaja perlu bersaiz 32TB! Oleh itu, menggunakan komputer klasik untuk mensimulasikan pengkomputeran kuantum sebenarnya adalah kaedah yang sangat memakan sumber. Sudah tentu, simulator pengkomputeran kuantum masih mempunyai nilai penyelidikan mereka Pada peringkat ini, apabila skala dan kualiti cip kuantum tidak dapat diperbaiki, simulator memainkan peranan penting. Pelaksanaan fungsi sihir dalam PythonJika pembaca perlu mengetahui pelaksanaan fungsi sihir yang terperinci dan menyeluruh dalam Python, mereka boleh mendapatkan dua artikel yang bagus daripada pautan rujukan artikel ini. Di sini kita hanya menumpukan pada beberapa fungsi yang boleh digunakan dalam kes penggunaan kod projectq di atas: __or__ dan __str__, dan kita boleh membuat pembiakan mudah bagi mereka.

Fungsi ajaib Python boleh digunakan untuk menentukan pengendali khas untuk kelas, seperti penambahan, penolakan, pendaraban dan pembahagian kelas Selepas fungsi ajaib diperkenalkan, tidak perlu mengendalikan elemen dalam kelas secara berasingan, dan operasi boleh dirangkumkan dengan fungsi ajaib. Kesan terakhir ialah kita boleh menggunakan operator secara langsung dalam kod untuk beroperasi pada kelas yang berbeza Sebagai contoh, kita boleh menyesuaikan operator binari seperti class1 + class2. Kami tidak akan memperkenalkannya secara terperinci dalam bab ini Anda boleh merujuk kepada contoh penggunaan khusus di bawah atau catatan blog dalam pautan.

Takrif dan pelaksanaan keadaan kuantum

Menurut pengenalan vektor keadaan kuantum dalam bab pertama, di sini kita boleh melaksanakan kelas keadaan kuantum mudah, dan kita hanya boleh mempertimbangkan dua qubit Sistem ringkas:

Takrifan kelas keadaan kuantum ini sangat mudah, ia adalah matriks 4&kali;1. Ia harus ditambah bahawa di sini kita mentakrifkan fungsi ajaib __str__(self), yang digunakan terutamanya untuk mencetak perwakilan rentetan kelas Sebagai contoh, di sini kita terus menukar vektor keadaan kuantum ke dalam format str dan kemudian mengeluarkannya. Kemudian jika kita mencetak kelas QubitPair tersuai, perwakilan rentetan bagi amplitud kebarangkalian sepadan dengan kelas semasa akan dipaparkan.

Takrifan dan pelaksanaan operasi get kuantum

Mengenai operasi get kuantum, kita boleh menganggapnya sebagai matriks yang bertindak pada vektor keadaan kuantum Di sini kita boleh menunjukkan Python operasi get yang ditentukan kelas kemudian mengembangkan dan menerangkannya:

# QubitPair.py
import numpy as np
 
class QubitPair:
    def __init__(self):
        self.state = np.array([1, 0, 0, 0], dtype=complex)
 
    def __str__(self):
        return str(self.state)

Takrifan matriks identiti dan matriks Pauli

这些是基本的泡利矩阵，这三个两能级体系的泡利矩阵具有非常好的物理性质，如都是酉矩阵且存在特殊的对易关系等：

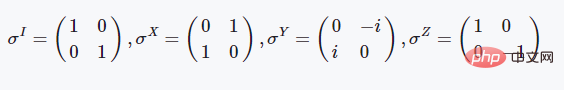
矩阵指数与旋转门操作

矩阵的指数计算一般采用泰勒级数展开的方法来进行定义：

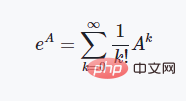
这里如果我们代入上述介绍的泡利矩阵就会得到这样的结果：

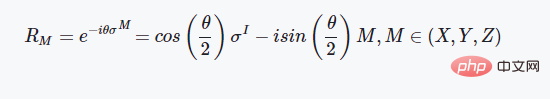
CX门操作的定义

在上述提到的所有的量子门操作中，CX是唯一的一个两比特量子门操作，也就是同时作用在两个量子比特上面，其矩阵形式的定义如下所示：

使用魔法函数__or__来实现量子门操作运算

我们首先简单谈一下为什么要用__or__这个魔法函数而不是其他的二元运算符来实现，这点跟开源库ProjectQ是同步的，理由是我们在量子力学中的运算，一般写成如下的形式：

|ψt〉=U|ψ0〉

将量子态写成狄拉克符号的形式，中文称为"左矢"和"右矢"，英文称之为"bra"和"ket"。因此竖线形式的定义，在形式上会更加契合量子力学的思维，当然，就算是换成其他的符号也是无可厚非的。

功能测试验证

在定义了量子态的类和量子门操作的类之后，我们可以写如下所示的一个测试脚本来测试程序的执行效果：

# TestQubits.py
from QubitPair import QubitPair
from Operator import QubitOperator
 
if __name__ == '__main__':
    qubits = QubitPair()
    print ('The initial state is: {}'.format(qubits))
    QubitOperator('X', 3.1415926, 0) | qubits
    print ('Applying X on the 0th qubit...')
    print ('The new state is: {}'.format(qubits))
    QubitOperator('CX') | qubits
    print ('Applying entanglement on qubits...')
    print ('The new state is: {}'.format(qubits))
    QubitOperator('X', 3.1415926, 0) | qubits
    print ('Applying X on the 0th qubit...')
    print ('The new state is: {}'.format(qubits))
    QubitOperator('CX') | qubits
    print ('Applying entanglement on qubits...')
    print ('The new state is: {}'.format(qubits))

这个程序的测试逻辑为：先定义一个两比特的量子系统，然后对第一个比特执行X门操作，使得其从|0〉态变成|1〉态，再对这两个比特执行纠缠门CX操作，观察其态的变化情况。之后再将第一个比特的状态变回|0〉态，再观察作用CX的态的变化情况，执行结果如下所示：

[dechin@dechin-manjaro simulator]$ python3 TestQubits.py 
The initial state is: [1.+0.j 0.+0.j 0.+0.j 0.+0.j]
Applying X on the 0th qubit...
The new state is: [2.67948966e-08+0.j 0.00000000e+00+0.j 0.00000000e+00-1.j
 0.00000000e+00+0.j]
Applying entanglement on qubits...
The new state is: [2.67948966e-08+0.j 0.00000000e+00+0.j 0.00000000e+00+0.j
 0.00000000e+00-1.j]
Applying X on the 0th qubit...
The new state is: [ 7.17966483e-16+0.00000000e+00j -1.00000000e+00+0.00000000e+00j
  0.00000000e+00-2.67948966e-08j  0.00000000e+00-2.67948966e-08j]
Applying entanglement on qubits...
The new state is: [ 7.17966483e-16+0.00000000e+00j -1.00000000e+00+0.00000000e+00j
  0.00000000e+00-2.67948966e-08j  0.00000000e+00-2.67948966e-08j]

这个结果所展示出来的数字也许比较乱，这是因为在运算过程中的计算精度不足所导致的，这里低于1e-06的数字其实我们可以认为就是0。那么我们从这个结果中可以分析总结出量子态的演变历程：

|00〉⇒|10〉⇒|11〉⇒|01〉⇒|01〉

注意：上面的这种写法，其实不太合乎程序语言的逻辑，一般从右到左的方向才是从低位到高位的写法。因此，严格来说写法应该是：|00〉⇒|01〉⇒|11〉⇒|10〉⇒|10〉。

这里我们就完成了基于魔法函数的量子计算模拟的过程，感兴趣的读者可以自行尝试更多的玩法，这里就不进行更多的测试了！

Atas ialah kandungan terperinci Apakah kaedah untuk melaksanakan fungsi ajaib dan simulasi pengkomputeran kuantum dalam Python?. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!