Rumah >Peranti teknologi >AI >Belajar = sesuai? Adakah pembelajaran mendalam dan statistik klasik adalah perkara yang sama?
Belajar = sesuai? Adakah pembelajaran mendalam dan statistik klasik adalah perkara yang sama?
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBke hadapan
- 2023-04-16 21:28:01768semak imbas
Dalam artikel ini, Boaz Barak, seorang saintis komputer teori dan profesor terkenal di Universiti Harvard, membandingkan perbezaan antara pembelajaran mendalam dan statistik klasik secara terperinci Dia percaya bahawa "jika anda memahami pembelajaran mendalam semata-mata dari perspektif statistik , anda akan mengabaikan keputusannya yang berjaya." faktor utama".
Pembelajaran mendalam (atau pembelajaran mesin secara umum) sering dianggap sebagai statistik semata-mata, iaitu pada asasnya konsep yang sama yang dikaji oleh ahli statistik, tetapi diterangkan menggunakan istilah yang berbeza daripada statistik. Rob Tibshirani pernah merumuskan "perbendaharaan kata" yang menarik ini di bawah:

Adakah sesuatu dalam senarai ini benar-benar bergema? Hampir sesiapa sahaja yang terlibat dalam pembelajaran mesin tahu bahawa banyak istilah di sebelah kanan jadual yang disiarkan oleh Tibshiriani digunakan secara meluas dalam pembelajaran mesin.
Jika anda memahami pembelajaran mendalam semata-mata daripada perspektif statistik, anda akan mengabaikan faktor utama kejayaannya. Penilaian pembelajaran mendalam yang lebih sesuai ialah ia menggunakan istilah statistik untuk menerangkan konsep yang sama sekali berbeza.
Penilaian pembelajaran mendalam yang betul bukanlah kerana ia menggunakan perkataan yang berbeza untuk menerangkan istilah statistik lama, tetapi ia menggunakan istilah ini untuk menerangkan proses yang sama sekali berbeza.
Artikel ini akan menerangkan sebab asas pembelajaran mendalam sebenarnya berbeza daripada statistik, malah berbeza daripada pembelajaran mesin klasik. Artikel ini mula-mula membincangkan perbezaan antara tugas "penjelasan" dan tugas "ramalan" apabila menyesuaikan model kepada data. Dua senario proses pembelajaran kemudiannya dibincangkan: 1. Memasang model statistik menggunakan pengurangan risiko empirikal 2. Mengajar kemahiran matematik kepada pelajar; Kemudian, artikel membincangkan senario mana yang lebih dekat dengan intipati pembelajaran mendalam.
Walaupun matematik dan kod untuk pembelajaran mendalam hampir sama dengan model statistik yang sesuai. Tetapi pada tahap yang lebih mendalam, pembelajaran mendalam lebih seperti mengajar kemahiran matematik kepada pelajar. Dan sepatutnya ada sangat sedikit orang yang berani mendakwa: Saya telah menguasai teori pembelajaran mendalam yang lengkap! Malah, adalah diragui sama ada teori sedemikian wujud. Sebaliknya, aspek pembelajaran mendalam yang berbeza difahami dengan baik dari perspektif yang berbeza, dan statistik sahaja tidak dapat memberikan gambaran yang lengkap.
Artikel ini membandingkan pembelajaran mendalam dan statistik di sini secara khusus merujuk kepada "statistik klasik" kerana ia telah dikaji untuk masa yang paling lama dan telah berada dalam buku teks untuk masa yang lama. Ramai ahli statistik sedang mengusahakan pembelajaran mendalam dan kaedah teori bukan klasik, sama seperti ahli fizik abad ke-20 diperlukan untuk mengembangkan rangka kerja fizik klasik. Malah, mengaburkan garis antara saintis komputer dan ahli statistik memberi manfaat kepada kedua-dua pihak.
Ramalan dan pemasangan model
Para saintis sentiasa membandingkan hasil pengiraan model dengan hasil pemerhatian sebenar untuk mengesahkan ketepatan model. Ahli astronomi Mesir Ptolemy mencadangkan model cerdik gerakan planet. Model Ptolemy mengikuti geosentrisme tetapi mempunyai satu siri epicycle (lihat rajah di bawah), memberikan ketepatan ramalan yang sangat baik. Sebaliknya, model heliosentrik asal Copernicus adalah lebih mudah daripada model Ptolemaic tetapi kurang tepat dalam meramalkan pemerhatian. (Copernicus kemudiannya menambah epicyclesnya sendiri untuk setanding dengan model Ptolemy.)
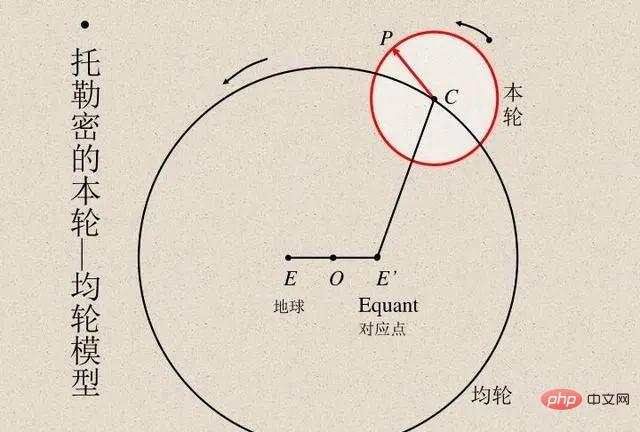
Kedua-dua model Ptolemy dan Copernicus tiada tandingannya. Jika kita ingin membuat ramalan dari "kotak hitam", maka model geosentrik Ptolemy adalah lebih unggul. Tetapi jika anda mahukan model mudah yang anda boleh "melihat ke dalam" (yang merupakan titik permulaan untuk teori yang menerangkan gerakan bintang), maka model Copernicus adalah cara untuk pergi. Kemudian, Kepler menambah baik model Copernicus kepada orbit elips dan mencadangkan tiga undang-undang pergerakan planet Kepler, yang membolehkan Newton menerangkan undang-undang planet dengan undang-undang graviti yang terpakai kepada bumi.
Oleh itu adalah penting bahawa model heliosentrik bukan sekadar "kotak hitam" yang menyediakan ramalan, tetapi diberikan oleh beberapa persamaan matematik mudah, tetapi dengan sangat sedikit "bahagian bergerak" dalam persamaan. Astronomi telah menjadi sumber inspirasi untuk membangunkan teknik statistik selama bertahun-tahun. Gauss dan Legendre secara bebas mencipta regresi kuasa dua terkecil sekitar tahun 1800 untuk meramalkan orbit asteroid dan jasad angkasa yang lain. Pada tahun 1847, Cauchy mencipta kaedah penurunan kecerunan, yang juga didorong oleh ramalan astronomi.
Dalam fizik, kadangkala sarjana boleh menguasai semua butiran untuk mencari teori "betul", mengoptimumkan ketepatan ramalan dan memberikan penjelasan terbaik tentang data. Ini adalah dalam skop idea seperti pisau cukur Occam, yang boleh dianggap sebagai mengandaikan bahawa kesederhanaan, kuasa ramalan dan kuasa penjelasan semuanya selaras antara satu sama lain.
Namun, dalam banyak bidang lain, hubungan antara dua matlamat penjelasan dan ramalan tidak begitu harmoni. Jika anda hanya ingin meramalkan pemerhatian, melalui "kotak hitam" mungkin adalah yang terbaik. Sebaliknya, jika seseorang ingin mendapatkan maklumat penjelasan, seperti model sebab akibat, prinsip umum, atau ciri penting, maka lebih mudah model yang boleh difahami dan dijelaskan, lebih baik.
Pilihan model yang betul bergantung pada tujuannya. Contohnya, pertimbangkan set data yang mengandungi ekspresi genetik dan fenotip bagi banyak individu (cth. beberapa penyakit jika matlamatnya adalah untuk meramalkan peluang seseorang untuk jatuh sakit, maka tidak kira betapa kompleksnya atau berapa banyak gen yang bergantung padanya, gunakan Model ramalan terbaik yang disesuaikan dengan tugas. Sebaliknya, jika tujuannya adalah untuk mengenal pasti beberapa gen untuk kajian lanjut, maka "kotak hitam" yang kompleks dan sangat tepat adalah penggunaan terhad.
Ahli statistik Leo Breiman menyatakan perkara ini dalam artikel 2001nya yang terkenal tentang Dua Budaya dalam Pemodelan Statistik. Yang pertama ialah "budaya pemodelan data" yang memfokuskan pada model generatif mudah yang boleh menerangkan data. Yang kedua ialah "budaya pemodelan algoritma" yang agnostik tentang cara data dijana dan memfokuskan pada mencari model yang boleh meramalkan data, tidak kira betapa rumitnya.

Tajuk kertas:
Pemodelan Statistik: Dua Budaya
Pautan kertas:
https://projecteuclid .
halang ahli statistik daripada mengkaji masalah baharu yang menarik
- Kertas Breiman menimbulkan beberapa kontroversi apabila ia keluar. Rakan perangkaan Brad Efron menjawab bahawa walaupun dia bersetuju dengan beberapa perkara, dia juga menekankan bahawa hujah Breiman nampaknya bertentangan dengan jimat cermat dan pandangan saintifik yang memihak kepada usaha keras untuk mencipta "kotak hitam" yang kompleks. Tetapi dalam artikel baru-baru ini, Efron meninggalkan pandangannya sebelum ini dan mengakui bahawa Breima lebih tepat kerana "fokus statistik pada abad ke-21 adalah pada algoritma ramalan, yang telah berkembang secara besar-besaran mengikut garis yang dicadangkan oleh Breiman."
- Model Ramalan Klasik dan Moden
Petikan daripada buku teks Duda dan Hart "Klasifikasi corak dan analisis adegan" dan kertas Highleyman 1962 "Reka Bentuk dan Analisis Eksperimen Pengecaman Corak".
Begitu juga, imej di bawah set data aksara tulisan tangan Highleyman dan seni bina yang digunakan untuk menyesuaikannya, Chow (1962) (ketepatan ~58%), akan bergema dengan ramai orang. 
Mengapa pembelajaran mendalam berbeza?
Pada tahun 1992, Geman, Bienenstock dan Doursat menulis artikel yang pesimis tentang rangkaian saraf, dengan alasan bahawa "rangkaian neural suapan semasa sebahagian besarnya tidak mencukupi untuk menyelesaikan masalah sukar dalam persepsi mesin dan pembelajaran mesin" . Secara khusus, mereka berpendapat bahawa rangkaian neural tujuan umum tidak akan berjaya mengendalikan tugas yang sukar, dan satu-satunya cara mereka boleh berjaya adalah melalui ciri yang direka bentuk secara buatan. Dalam kata-kata mereka: "Sifat penting mesti terbina dalam atau "berwayar keras"... dan bukannya dipelajari dalam apa-apa erti kata statistik Sekarang nampaknya Geman et al benar-benar salah, tetapi ia lebih menarik untuk difahami mengapa mereka Salah. 
(
ialah matriks;
ialah vektor berdimensi2. Gunakan data di atas untuk memuatkan model  dan gunakan algoritma pengoptimuman untuk meminimumkan risiko empirikal. Maksudnya, cari
dan gunakan algoritma pengoptimuman untuk meminimumkan risiko empirikal. Maksudnya, cari  sedemikian melalui algoritma pengoptimuman supaya
sedemikian melalui algoritma pengoptimuman supaya 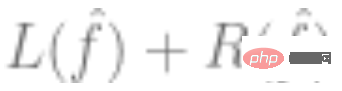 ialah yang terkecil,
ialah yang terkecil,  mewakili kerugian (menunjukkan betapa hampirnya nilai ramalan dengan nilai sebenar), dan
mewakili kerugian (menunjukkan betapa hampirnya nilai ramalan dengan nilai sebenar), dan  adalah pilihan istilah regularisasi.
adalah pilihan istilah regularisasi.
3. Lebih kecil kehilangan keseluruhan model, lebih baik, iaitu nilai ralat generalisasi 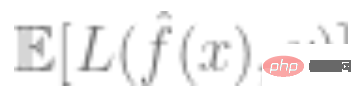 adalah agak minimum.
adalah agak minimum.
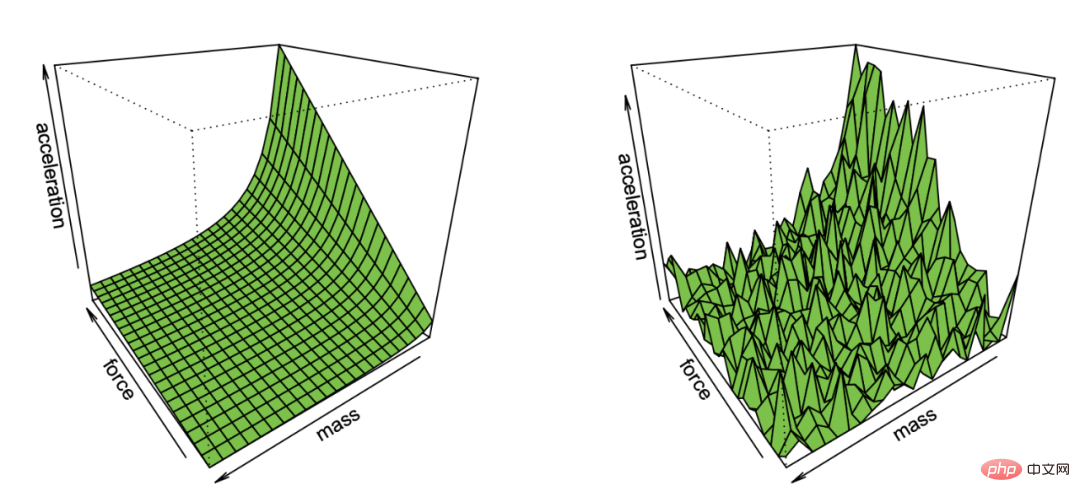
Ilustrasi Effron tentang memulihkan hukum pertama Newton daripada pemerhatian yang mengandungi hingar
Contoh yang sangat umum ini sebenarnya mengandungi banyak perkara, seperti kuasa dua terkecil Regresi linear, jiran terdekat , latihan rangkaian saraf dan banyak lagi. Dalam senario statistik klasik, kami biasanya menghadapi situasi berikut:
Perdagangan: Dengan mengandaikan koleksi model yang dioptimumkan (jika fungsi itu bukan cembung atau mengandungi istilah regularisasi, pilihan algoritma dan penetapan yang teliti boleh Dapatkan set model. Bias ialah anggaran yang paling hampir dengan nilai sebenar yang boleh dicapai oleh sesuatu elemen, semakin kecil set itu, dan mungkin 0 jika
. lebih besar varians model keluaran algoritma Ralat generalisasi keseluruhan adalah jumlah bias dan varians Oleh itu, pembelajaran statistik biasanya merupakan pertukaran Bias-Variance, dan kerumitan model yang betul adalah untuk meminimumkan ralat keseluruhan , Geman et al. menunjukkan pesimisme mereka tentang rangkaian saraf dengan berhujah bahawa had asas yang ditimbulkan oleh dilema Bias-Variance digunakan untuk semua model inferens bukan parametrik, termasuk rangkaian saraf
"Lebih banyak lagi meriah" tidak terpakai . Sentiasa benar: Dalam pembelajaran statistik, lebih banyak ciri atau data tidak semestinya meningkatkan prestasi Sebagai contoh, sukar untuk belajar daripada data yang mengandungi banyak ciri yang tidak berkaitan satu daripada dua pengedaran (seperti dan , adalah lebih sukar daripada mempelajari setiap pengedaran secara bebas.
Pulangan berkurangan: Dalam banyak kes, bilangan titik data yang diperlukan untuk mengurangkan hingar ramalan ke tahap adalah sama dengan jumlah parameter Berkaitan, iaitu, bilangan titik data adalah lebih kurang sama dengan . Dalam kes ini, kira-kira k sampel diperlukan untuk memulakan, tetapi sebaik sahaja anda melakukan ini, anda menghadapi pulangan yang semakin berkurangan, iaitu jika anda memerlukan 90% mata untuk mencapai ketepatan 90%. , Ia memerlukan kira-kira 10 mata tambahan untuk meningkatkan ketepatan kepada 95%. >
Pergantungan berat pada kehilangan, data: Apabila menyesuaikan model dengan data berdimensi tinggi, sebarang butiran kecil boleh membuat perbezaan besar dalam pilihan seperti L1 atau L2 regularizers Apatah lagi menggunakan set data yang berbeza pengoptimum berdimensi tinggi juga sangat berbeza antara satu sama lain Data ini secara relatifnya "naif": biasanya diandaikan bahawa data adalah bebas daripada beberapa sampel Walaupun titik yang hampir dengan sempadan keputusan adalah sukar untuk diklasifikasikan fenomena kepekatan pengukuran dalam dimensi tinggi, boleh dianggap bahawa jarak antara titik data adalah serupa dalam pengedaran data klasik Walau bagaimanapun, model campuran boleh menunjukkan perbezaan ini, jadi tidak seperti masalah lain di atas. perbezaan ini adalah perkara biasa dalam statistik Senario B: Pembelajaran Matematik Dalam senario ini, kami menganggap anda ingin mengajar pelajar matematik (seperti mengira terbitan) melalui beberapa arahan dan latihan senario ini , walaupun tidak ditakrifkan secara formal, mempunyai beberapa ciri kualitatif:Pelajari kemahiran daripada menghampiri taburan statistik: Dalam kes ini, pelajar mempelajari kemahiran dan bukannya anggaran/ramalan daripada sesuatu kuantiti. Khususnya, walaupun fungsi yang memetakan latihan kepada penyelesaian tidak boleh digunakan sebagai "kotak hitam" untuk menyelesaikan tugasan yang tidak diketahui tertentu, model mental yang dibangunkan pelajar semasa menyelesaikan masalah ini masih boleh berguna untuk tugasan yang tidak diketahui. 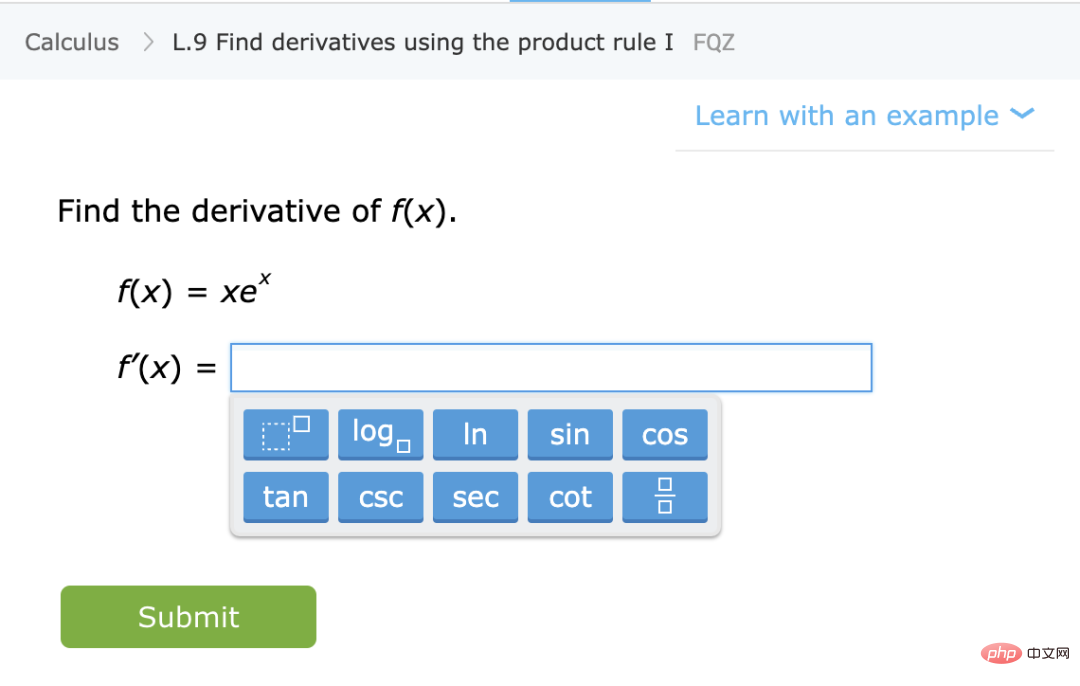
Daripada meningkatkan keupayaan kepada perwakilan automatik: Walaupun terdapat juga pengurangan pulangan kepada penyelesaian masalah dalam beberapa kes, pelajar belajar melalui beberapa peringkat. Terdapat peringkat di mana menyelesaikan beberapa masalah membantu memahami konsep dan membuka kunci kebolehan baharu. Di samping itu, apabila pelajar mengulangi jenis masalah tertentu, mereka akan membentuk proses penyelesaian masalah automatik apabila mereka melihat masalah yang serupa, berubah daripada peningkatan keupayaan sebelumnya kepada penyelesaian masalah automatik.
Prestasi bebas daripada data dan kerugian: Terdapat lebih daripada satu cara untuk mengajar konsep matematik. Pelajar yang belajar menggunakan buku yang berbeza, kaedah pendidikan atau sistem penggredan boleh akhirnya mempelajari kandungan yang sama dan mempunyai kebolehan matematik yang serupa.
Sesetengah masalah lebih sukar: Dalam latihan matematik kita sering melihat perkaitan yang kuat antara cara pelajar berbeza menyelesaikan masalah yang sama. Nampaknya terdapat tahap kesukaran yang wujud untuk masalah, dan perkembangan semula jadi kesukaran yang terbaik untuk pembelajaran.
Pembelajaran mendalam lebih kepada anggaran statistik atau kemahiran belajar pelajar?
Dari dua metafora di atas, yang manakah lebih sesuai untuk menggambarkan pembelajaran mendalam moden? Secara khusus, apakah yang menjadikannya berjaya? Pemasangan model statistik boleh dinyatakan dengan baik menggunakan matematik dan kod. Malah, gelung latihan Pytorch kanonik melatih rangkaian yang mendalam melalui pengurangan risiko empirikal:

Pada tahap yang lebih mendalam, hubungan antara kedua-dua senario ini tidak jelas. Untuk lebih spesifik, berikut adalah tugas pembelajaran khusus sebagai contoh. Pertimbangkan algoritma klasifikasi yang dilatih menggunakan pendekatan "pembelajaran diselia sendiri + pengesanan linear". Latihan algoritma khusus adalah seperti berikut:
1 Andaikan bahawa data ialah urutan, dengan  ialah titik data tertentu (seperti gambar) dan merupakan label.
ialah titik data tertentu (seperti gambar) dan merupakan label.
2. Mula-mula dapatkan rangkaian saraf dalam yang mewakili fungsi 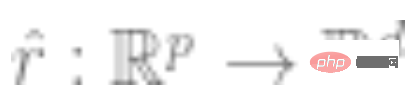 . Fungsi kehilangan yang diselia sendiri dari beberapa jenis dilatih dengan meminimumkannya hanya menggunakan titik data dan bukan label. Contoh fungsi kehilangan tersebut ialah pembinaan semula (memulihkan input dengan input lain) atau pembelajaran kontrastif (idea teras adalah untuk membandingkan sampel positif dan negatif dalam ruang ciri untuk mempelajari perwakilan ciri sampel).
. Fungsi kehilangan yang diselia sendiri dari beberapa jenis dilatih dengan meminimumkannya hanya menggunakan titik data dan bukan label. Contoh fungsi kehilangan tersebut ialah pembinaan semula (memulihkan input dengan input lain) atau pembelajaran kontrastif (idea teras adalah untuk membandingkan sampel positif dan negatif dalam ruang ciri untuk mempelajari perwakilan ciri sampel).
3. Pasangkan pengelas linear 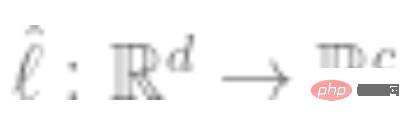 (ialah bilangan kelas) menggunakan data berlabel lengkap untuk meminimumkan kehilangan entropi silang. Pengelas akhir kami ialah:
(ialah bilangan kelas) menggunakan data berlabel lengkap untuk meminimumkan kehilangan entropi silang. Pengelas akhir kami ialah:
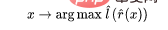
Langkah 3 hanya berfungsi untuk pengelas linear, jadi "keajaiban" berlaku dalam langkah 2 (pembelajaran rangkaian dalam yang diselia sendiri). Terdapat beberapa sifat penting dalam pembelajaran penyeliaan kendiri:
Pelajari kemahiran daripada menghampiri fungsi: Pembelajaran penyeliaan kendiri bukan tentang menghampiri fungsi, tetapi perwakilan pembelajaran yang boleh digunakan untuk pelbagai tugas hiliran (ini adalah paradigma dominan pemprosesan bahasa semula jadi). Mendapatkan tugas hiliran melalui probing linear, penalaan halus atau pengujaan adalah kedua.
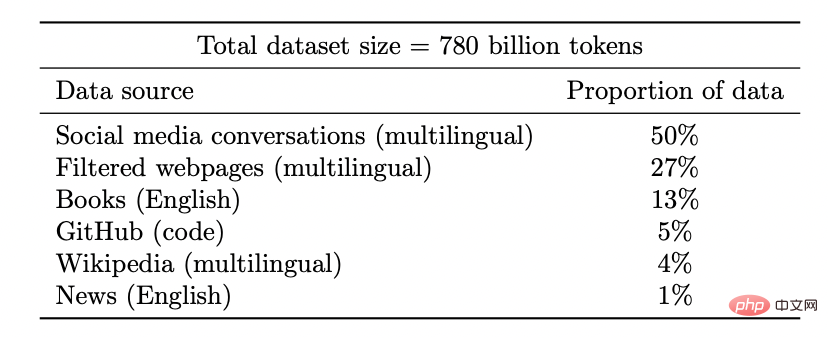
Lebih banyak lagi meriah: Dalam pembelajaran penyeliaan kendiri, kualiti perwakilan bertambah baik apabila jumlah data meningkat dan tidak menjadi lebih teruk dengan mencampurkan data daripada beberapa sumber. Malah, lebih pelbagai data, lebih baik.
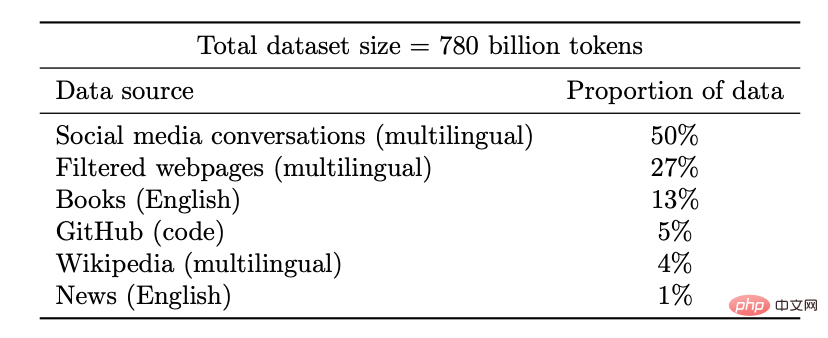
Set data model Coogle PaLM
Membuka kunci keupayaan baharu: Apabila pelaburan sumber (data, pengiraan, saiz model) meningkat, model pembelajaran mendalam juga bertambah baik secara tidak berterusan. Ini juga telah ditunjukkan dalam beberapa persekitaran gabungan.
Apabila saiz model bertambah, PaLM menunjukkan peningkatan diskret dalam penanda aras dan membuka kunci ciri yang mengejutkan, seperti menerangkan sebab jenaka itu lucu.
Prestasi hampir bebas daripada kehilangan atau data: terdapat berbilang kerugian yang diselia sendiri, berbilang kontras dan kerugian pembinaan semula sebenarnya digunakan dalam penyelidikan imej, model bahasa menggunakan pembinaan semula satu sisi (meramalkan token seterusnya) atau menggunakan model topeng , ramalkan input topeng dari token kiri dan kanan. Anda juga boleh menggunakan set data yang sedikit berbeza. Ini mungkin menjejaskan kecekapan, tetapi selagi pilihan "munasabah" dibuat, selalunya sumber asal meningkatkan prestasi ramalan lebih daripada kehilangan atau set data khusus yang digunakan.
Sesetengah kes lebih sukar daripada yang lain: perkara ini tidak khusus untuk pembelajaran diselia sendiri. Titik data nampaknya mempunyai beberapa "tahap kesukaran" yang wujud. Sebenarnya, algoritma pembelajaran yang berbeza mempunyai "tahap kemahiran" yang berbeza, dan dian data yang berbeza mempunyai "tahap kesukaran" yang berbeza (kebarangkalian pengelas dengan betul mengelaskan sesuatu mata meningkat secara monoton dengan kemahiran dan menurun secara monoton dengan kesukaran).
Paradigma "kemahiran vs. kesukaran" ialah penjelasan paling jelas tentang fenomena "ketepatan pada baris" yang ditemui oleh Recht et al dan Miller et al. Makalah oleh Kaplen, Ghosh, Garg, dan Nakkiran juga menunjukkan bagaimana input yang berbeza dalam set data mempunyai "profil kesukaran" yang sedia ada yang secara amnya teguh kepada keluarga model yang berbeza.
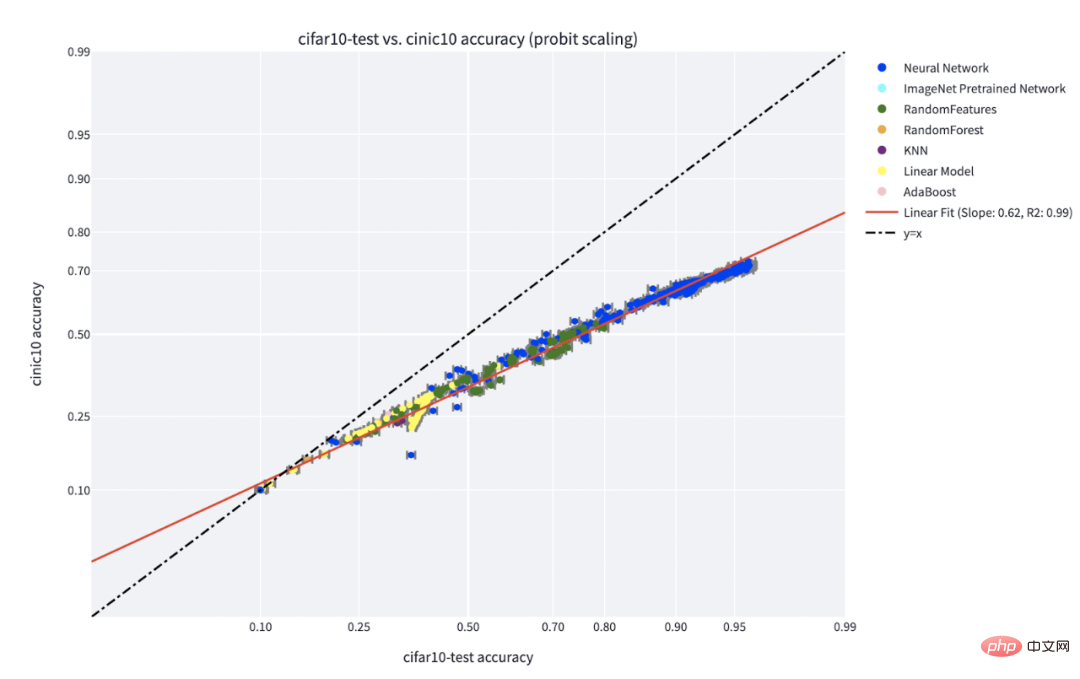
Ketepatan C** pada fenomena talian untuk pengelas yang dilatih pada IFAR-10 dan diuji pada CINIC-10. Sumber angka: https://millerjohnp-linearfits-app-app-ryiwcq.streamlitapp.com/
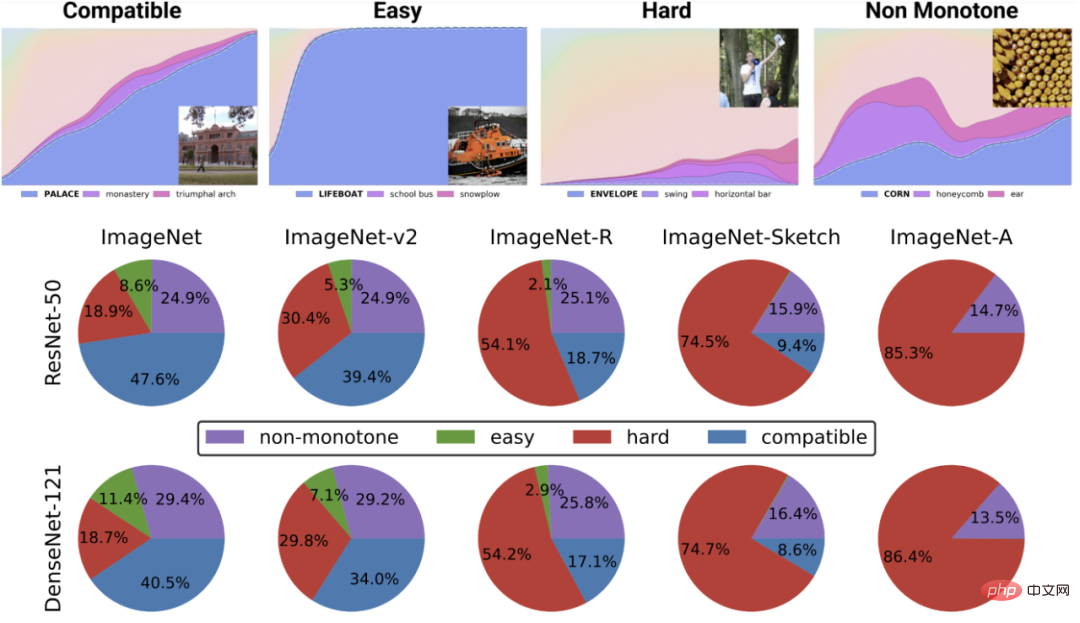
Angka teratas menggambarkan kebarangkalian softmax yang berbeza untuk kelas yang paling berkemungkinan, sebagai Fungsi ketepatan global pengelas untuk kelas yang diindeks mengikut masa latihan. Carta pai bawah menunjukkan penguraian set data yang berbeza kepada jenis titik yang berbeza (perhatikan bahawa penguraian ini adalah serupa untuk struktur saraf yang berbeza).
Latihan ialah pengajaran: Latihan model besar moden kelihatan lebih seperti mengajar pelajar daripada membiarkan model itu sesuai dengan data Apabila pelajar tidak faham atau berasa letih, mereka "berehat" atau mencuba kaedah yang berbeza (latihan perbezaan). Log latihan model besar Meta adalah instruktif - sebagai tambahan kepada isu perkakasan, kami juga boleh melihat campur tangan seperti menukar algoritma pengoptimuman yang berbeza semasa latihan, dan juga mempertimbangkan fungsi pengaktifan "pertukaran panas" (GELU kepada RELU). Yang terakhir tidak masuk akal jika anda menganggap latihan model sebagai sesuai dengan data, dan bukannya mempelajari perwakilan.
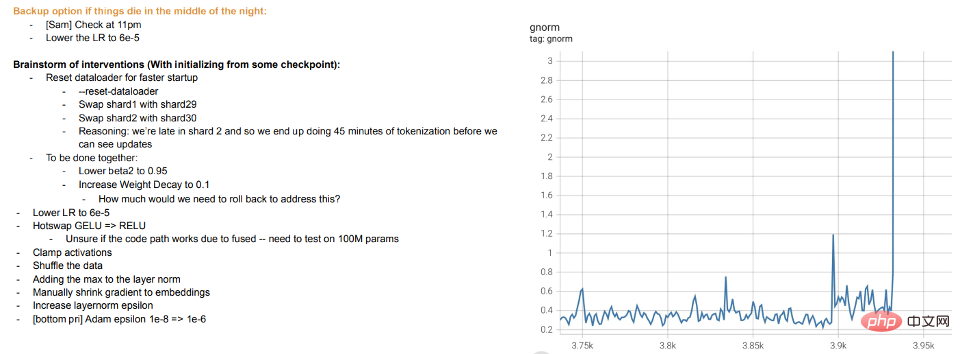
Petikan log latihan meta
4.1 Tetapi bagaimana pula dengan pembelajaran diselia?
Pembelajaran penyeliaan kendiri telah dibincangkan lebih awal, tetapi contoh tipikal pembelajaran mendalam adalah pembelajaran penyeliaan. Lagipun, "Momen ImageNet" pembelajaran mendalam datang daripada ImageNet. Jadi adakah perkara yang dibincangkan di atas masih terpakai pada tetapan ini?
Pertama, kemunculan pembelajaran mendalam berskala besar yang diselia agak tidak disengajakan, hasil daripada ketersediaan set data berlabel yang besar dan berkualiti tinggi (iaitu, ImageNet). Jika anda mempunyai imaginasi yang baik, anda boleh bayangkan sejarah alternatif di mana pembelajaran mendalam mula-mula membuat penemuan dalam pemprosesan bahasa semula jadi melalui pembelajaran tanpa pengawasan, sebelum beralih kepada pembelajaran visi dan diselia.
Kedua, terdapat bukti bahawa pembelajaran seliaan dan pembelajaran seliaan sendiri berkelakuan "secara dalaman" sama walaupun menggunakan fungsi kerugian yang berbeza sama sekali. Kedua-duanya biasanya mencapai prestasi yang sama. Khususnya, bagi setiap satu, seseorang boleh menggabungkan lapisan k pertama bagi model kedalaman d terlatih dengan penyeliaan diri dengan lapisan d-k terakhir model diselia dengan kehilangan prestasi yang sedikit.
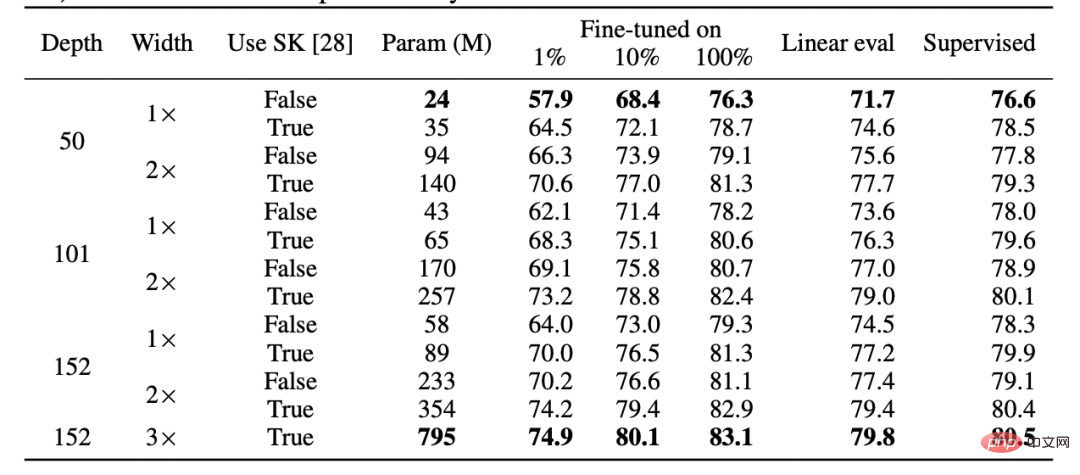
Jadual daripada kertas SimCLR v2. Perhatikan persamaan umum dalam prestasi antara pembelajaran diselia, penalaan halus (100%) penyeliaan sendiri dan pengesanan linear penyeliaan sendiri (Sumber: https://arxiv.org/abs/2006.10029)
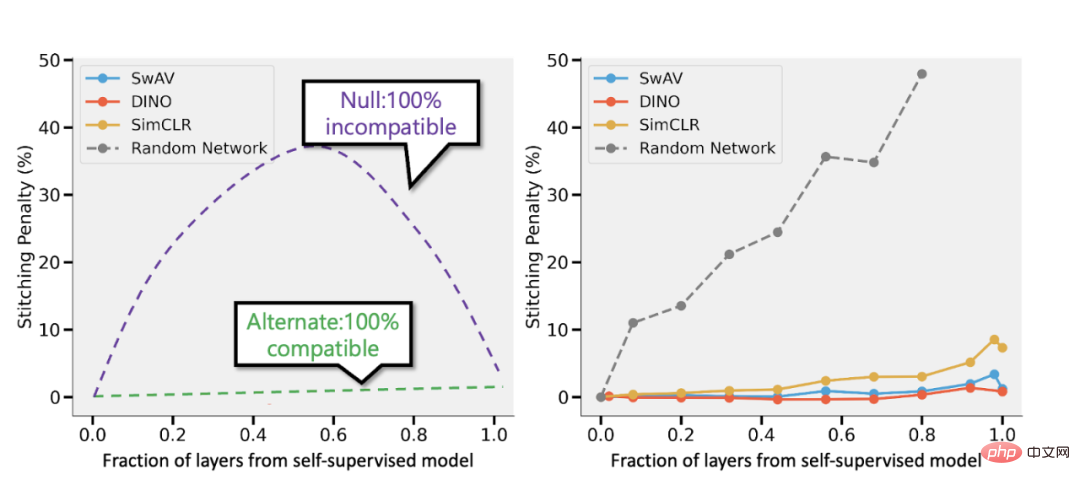
Sambungkan model seliaan sendiri dan model seliaan Bansal et al. (https://arxiv.org/abs/2106.07682). Kiri: Jika ketepatan model penyeliaan sendiri adalah (katakan) 3% lebih rendah daripada model diselia, maka perwakilan yang serasi sepenuhnya akan menghasilkan penalti penyambungan sebanyak p 3% apabila bahagian p lapisan datang daripada penyeliaan sendiri. model. Jika model tidak serasi sepenuhnya, maka kami menjangkakan ketepatan akan menurun secara mendadak apabila lebih banyak model digabungkan. Kanan: Hasil sebenar menggabungkan model yang diselia sendiri yang berbeza.
Kelebihan model penyeliaan sendiri + ringkas ialah model ini boleh menggabungkan pembelajaran ciri atau "sihir pembelajaran mendalam" (dilakukan oleh fungsi perwakilan mendalam) dengan pemasangan model statistik (dilakukan oleh pengelas linear atau "mudah" lain di sini Menunjukkan siap di atas) pemisahan.
Akhirnya, walaupun ini lebih kepada spekulasi, hakikatnya "pembelajaran meta" selalunya seolah-olah disamakan dengan perwakilan pembelajaran (lihat: https://arxiv.org/abs/1909.09157, https: //arxiv .org/abs/2206.03271), yang boleh dilihat sebagai bukti lain bahawa ini sebahagian besarnya dilakukan tanpa mengira matlamat pengoptimuman model.
4.2 Apa yang perlu dilakukan mengenai penparameteran berlebihan?
Artikel ini melangkau perkara yang dianggap sebagai contoh klasik perbezaan antara model pembelajaran statistik dan pembelajaran mendalam dalam amalan: kekurangan "pertukaran Bias-Variance" dan keupayaan model terparameter berlebihan untuk membuat generalisasi baiklah.
Mengapa ponteng? Terdapat dua sebab:
- Pertama sekali, jika pembelajaran penyeliaan sememangnya sama dengan pembelajaran penyeliaan sendiri + mudah, maka ini mungkin menjelaskan keupayaan generalisasinya.
- Kedua, penparameteran berlebihan bukanlah kunci kejayaan pembelajaran mendalam. Apa yang menjadikan rangkaian dalam istimewa bukan kerana ia besar berbanding bilangan sampel, tetapi ia besar secara mutlak. Malah, biasanya dalam pembelajaran tanpa pengawasan/penyeliaan kendiri, model tersebut tidak terlalu diparameterkan. Walaupun untuk model bahasa yang sangat besar, set data mereka lebih besar.

Kertas "deep bootstrap" Nakkiran-Neyshabur-Sadghi menunjukkan bahawa seni bina moden berkelakuan serupa dalam rejim "over-parameterized" atau "under-sampled" ( model dalam Latihan untuk berbilang zaman pada data terhad sehingga terlalu muat: "Dunia Sebenar" dalam rajah di atas), juga dalam keadaan "diparameterkan" atau "dalam talian" (model dilatih untuk satu zaman, dan setiap sampel adalah hanya dilihat sekali: "Dunia Ideal" gambar di atas). Sumber imej: https://arxiv.org/abs/2010.08127
Ringkasan
Pembelajaran statistik sememangnya memainkan peranan dalam pembelajaran mendalam. Walau bagaimanapun, walaupun menggunakan istilah dan kod yang serupa, melihat pembelajaran mendalam sebagai sekadar menyesuaikan model dengan lebih banyak parameter daripada model klasik terlepas banyak perkara yang penting untuk kejayaannya. Metafora untuk mengajar pelajar matematik juga tidak sempurna.
Seperti evolusi biologi, walaupun pembelajaran mendalam mengandungi banyak peraturan yang digunakan semula (seperti keturunan kecerunan dengan kehilangan pengalaman), ia boleh menghasilkan hasil yang sangat kompleks. Nampaknya pada masa yang berbeza, komponen rangkaian yang berbeza mempelajari perkara yang berbeza, termasuk pembelajaran perwakilan, pemasangan ramalan, penyusunan tersirat dan hingar tulen. Penyelidik masih mencari lensa yang sesuai untuk bertanya soalan tentang pembelajaran mendalam, apatah lagi menjawabnya.
Atas ialah kandungan terperinci Belajar = sesuai? Adakah pembelajaran mendalam dan statistik klasik adalah perkara yang sama?. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!
Artikel berkaitan
Lihat lagi- Aliran teknologi untuk ditonton pada tahun 2023
- Cara Kecerdasan Buatan Membawa Kerja Baharu Setiap Hari kepada Pasukan Pusat Data
- Bolehkah kecerdasan buatan atau automasi menyelesaikan masalah kecekapan tenaga yang rendah dalam bangunan?
- Pengasas bersama OpenAI ditemu bual oleh Huang Renxun: Keupayaan penaakulan GPT-4 belum mencapai jangkaan
- Bing Microsoft mengatasi Google dalam trafik carian terima kasih kepada teknologi OpenAI

