Gunakan Python untuk melaksanakan pengesanan automatik peluru berpandu, sangat terbakar!

Hello semua, saya Abang J.

Ini sukar untuk dikira tanpa asas matematik. Tetapi berbeza apabila kita mempunyai komputer Bergantung pada kelajuan pengkomputeran yang sangat pantas, kita boleh mencapainya dengan menggunakan idea pembezaan dan menambah sedikit pengetahuan mudah tentang trigonometri.

Baiklah, tanpa berlengah lagi, mari kita lihat prinsip algoritmanya dan lihat gambar:

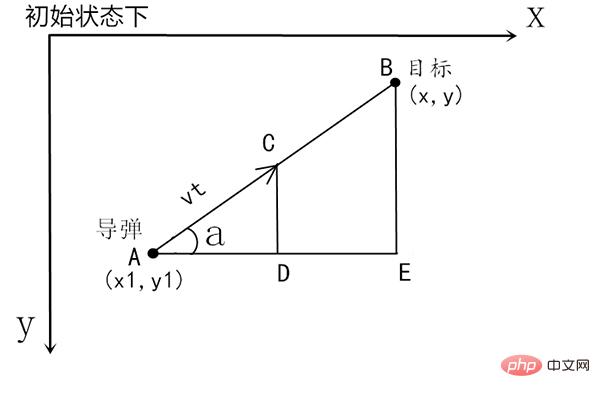
Memandangkan kita akan menggunakan pygame untuk menunjukkannya kemudian , Sistem koordinatnya ialah dengan paksi-y menghala ke bawah, jadi di sini kita juga menggunakan sistem koordinat dengan paksi-y menghala ke bawah.

Idea umum algoritma adalah untuk membahagikan masa t kepada segmen yang cukup kecil (seperti 1/1000, lebih kecil potongan masa, lebih tepat ia) berdasarkan rajah di atas segmen membina segi tiga seperti yang ditunjukkan di atas untuk mengira peluru berpandu Arah berjalan dalam hirisan masa berikutnya (iaitu ∠a) dan jarak yang dilalui (iaitu vt=|AC| Pada masa ini, sasaran bergerak semula dalam detik hirisan masa Pada masa ini, titik C yang baru dikira menjadi Titik awal hirisan kali kedua, kemudian bina segitiga pada titik C dan titik sasaran baharu pada hirisan kali kedua untuk mengira vt baharu, dan kemudian masukkan yang ketiga. potong masa, dan ulangi.

Andaikan bahawa koordinat peluru berpandu dan sasaran dalam keadaan awal ialah (x1, y1), (x, y) masing-masing, dan bina segi tiga tepat ABE. Segitiga ini digunakan untuk mencari sinus dan kosinus nilai ∠a, kerana vt Ia ditetapkan oleh kita sendiri Kita perlu mengira berapa banyak koordinat x dan y bagi titik A telah bergerak masing-masing boleh didarab dengan vt cos(a) dan sin(a) masing-masing.

Kira sin(a) dan cos(a), sinus lwn. cerun, kosinus lwn cerun, dan hipotenus boleh dikira menggunakan formula jarak dua titik, iaitu:

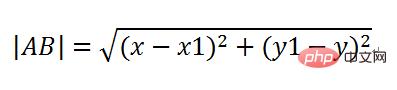
Jadi

Panjang AC ialah kelajuan peluru berpandu yang didarab dengan masa, iaitu |AC|=vt, dan kemudian panjang AD dan CD boleh dikira, jadi ini Selepas hirisan masa berlalu, peluru berpandu harus muncul di titik kedudukan baru C, dan koordinatnya ialah x tambah AD dan y tolak CD titik lama A.

Jadi, koordinat baharu titik C ialah:

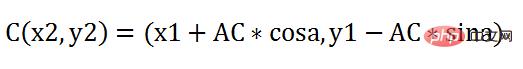
Teruskan lakukan operasi ini berulang kali, untuk menjadi lebih jelas, letakkan yang pertama Lihat pada kepingan kali pertama dan kepingan kali kedua bersama-sama:

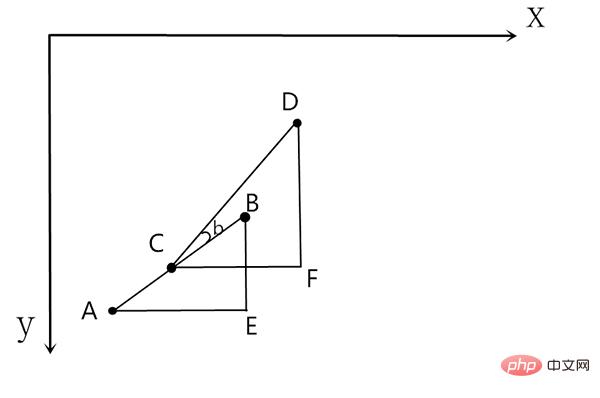
Yang pertama ialah segi tiga yang dibina oleh kepingan masa ialah ABE. sasaran Dari titik B ke titik D, peluru berpandu kini berada di titik C, jadi kami membina segitiga baru CDF dan ulangi proses pengiraan tadi Sudut ∠b dalam gambar ialah sudut di mana peluru berpandu perlu berputar. Pada hakikatnya, ia hanya mengambil setiap masa Hanya betulkan arah peluru berpandu dengan sekeping filem Bagaimana untuk menukar arah peluru berpandu tidak menjadi masalah yang perlu kita kaji

Baiklah, kerana saya telah menggunakan. Pustaka pygame Python untuk membuat permainan kecil baru-baru ini, kami akan menggunakan pygame seterusnya untuk menunjukkan kesan ini:

Kod yang sangat mudah adalah seperti berikut: <.>

import pygame,sys
from math import *
pygame.init()
screen=pygame.display.set_mode((800,700),0,32)
missile=pygame.image.load('element/red_pointer.png').convert_alpha()
x1,y1=100,600 #导弹的初始发射位置
velocity=800#导弹速度
time=1/1000 #每个时间片的长度
clock=pygame.time.Clock()
old_angle=0
while True:
for event in pygame.event.get():
if event.type==pygame.QUIT:
sys.exit()
clock.tick(300)
x,y=pygame.mouse.get_pos()#获取鼠标位置，鼠标就是需要打击的目标
distance=sqrt(pow(x1-x,2)+pow(y1-y,2))#两点距离公式
section=velocity*time #每个时间片需要移动的距离
sina=(y1-y)/distance
cosa=(x-x1)/distance
angle=atan2(y-y1,x-x1)#两点线段的弧度值
x1,y1=(x1+section*cosa,y1-section*sina)
d_angle = degrees(angle)#弧度转角度
screen.blit(missile, (x1-missile.get_width(), y1-missile.get_height()/2))
dis_angle=d_angle-old_angle#dis_angle就是到下一个位置需要改变的角度
old_angle=d_angle#更新初始角度
pygame.display.update()

Jika peluru berpandu hanya dianggap sebagai zarah Jika ya, maka algoritma di atas sudah cukup saya tidak melakukan putaran peluru berpandu, kerana zarah tidak perlu diputar sama ada kepala atau ekor Sudah tentu, premis ini ialah apabila imej peluru berpandu yang anda muatkan sangat kecil, ia akan kelihatan baik jika ia tidak berputar. Tetapi melakukan putaran dalam pygame bukanlah satu tugas yang mudah Mari kita menggantikan gambar dengan segi empat tepat, dan kemudian menambah fungsi putaran untuk melihat kesan

missiled = pygame.transform.rotate(missile, -(d_angle))
screen.blit(missiled, (x1-missile.get_width(), y1-
missile.get_height()/2))

Kerana titik koordinat gambar ialah titik di sudut kiri atasnya, jika kita mahu koordinat gambar ditetapkan pada hujung anak panah, maka hanya kurangkan kedudukan cetakan sebenar x gambar dengan mengurangkan panjang gambar dan y dengan mengurangkan lebar separuh. Tetapi kesan operasi sebenar tidak baik:

大致方向相同，但是图片箭头的尖点并没有一直跟随鼠标，这是为什么呢。经过一番研究，我发现原来是这个图旋转的机制问题，我们看看旋转后的图片变成什么样了：

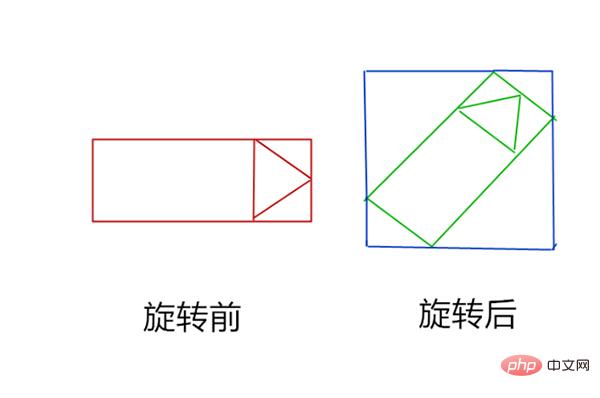
旋转后的图片变成了蓝色的那个范围，根据旋转角度的不同，所变成的图片大小也不一样，我们看旋转90的情况

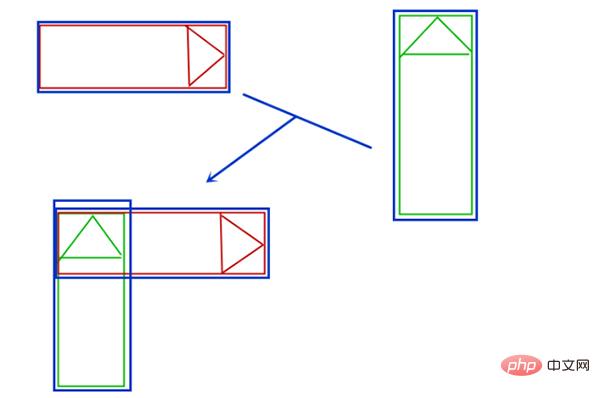
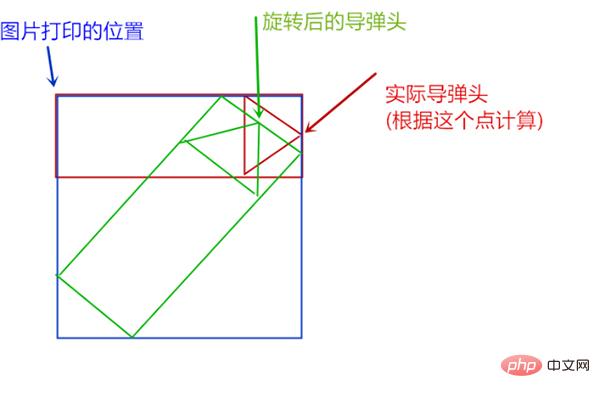
我们发现，旋转后的图片不仅面积变大了，导弹头的位置也变了。那应该怎么解决这个问题呢？思路是，每一次旋转图片以后，求出旋转图的头位置（图中的绿色箭头点），然后把绿图的打印位置移动一下，下，x，y分别移动两个头的距离，就可以让旋转后的导弹头对准实际我们参与运算的那个导弹头的位置，移动后应该是这样的：

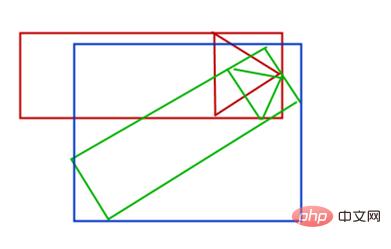
这样，两个导弹头的点就一致了。接下来我们分析求旋转后的导弹头的算法。根据旋转角度的不同，旋转角在不同象限参数不一样，所以我们分为这四种情况

1，2象限

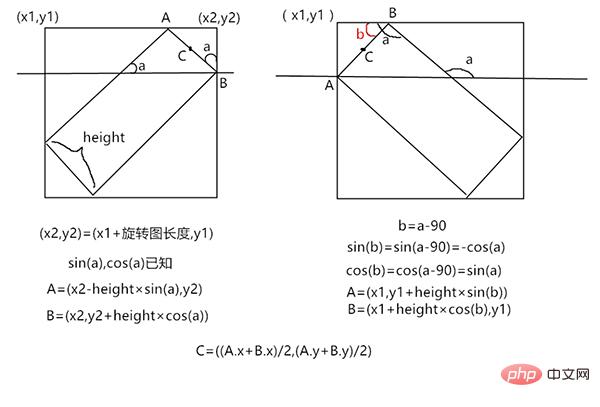
3，4象限，它的旋转只有正负0—180，所以3，4象限就是负角

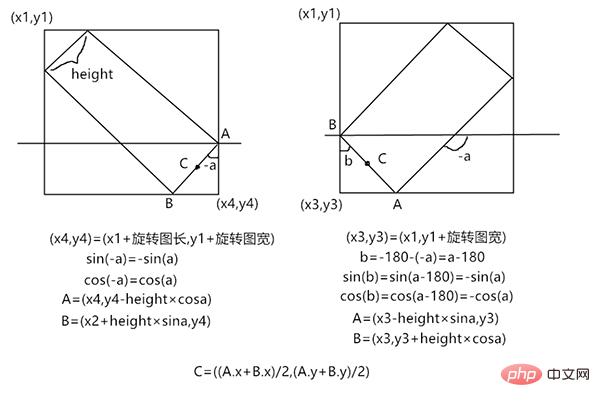
显示图片的时候我们将他移动

screen.blit(missiled, (x1-width+(x1-C[0]),y1-height/2+(y1-C[1])))

这里的 (x1-width, y1-height/2) 其实才是上图中的 (x1, y1)  

所以最后我们加入相关算法代码，效果就比较完美了

大功告成，最后附上全部的算法代码

import pygame,sys
from math import *
pygame.init()
font1=pygame.font.SysFont('microsoftyaheimicrosoftyaheiui',23)
textc=font1.render('*',True,(250,0,0))
screen=pygame.display.set_mode((800,700),0,32)
missile=pygame.image.load('element/rect1.png').convert_alpha()
height=missile.get_height()
width=missile.get_width()
pygame.mouse.set_visible(0)
x1,y1=100,600 #导弹的初始发射位置
velocity=800#导弹速度
time=1/1000 #每个时间片的长度
clock=pygame.time.Clock()
A=()
B=()
C=()
while True:
for event in pygame.event.get():
if event.type==pygame.QUIT:
sys.exit()
clock.tick(300)
x,y=pygame.mouse.get_pos()#获取鼠标位置，鼠标就是需要打击的目标
distance=sqrt(pow(x1-x,2)+pow(y1-y,2))#两点距离公式
section=velocity*time #每个时间片需要移动的距离
sina=(y1-y)/distance
cosa=(x-x1)/distance
angle=atan2(y-y1,x-x1)#两点间线段的弧度值
fangle=degrees(angle) #弧度转角度
x1,y1=(x1+section*cosa,y1-section*sina)
missiled=pygame.transform.rotate(missile,-(fangle))
if 0<=-fangle<=90:
A=(width*cosa+x1-width,y1-height/2)
B=(A[0]+height*sina,A[1]+height*cosa)
if 90<-fangle<=180:
A = (x1 - width, y1 - height/2+height*(-cosa))
B = (x1 - width+height*sina, y1 - height/2)
if -90<=-fangle<0:
A = (x1 - width+missiled.get_width(), y1 - height/2+missiled.get_height()-height*cosa)
B = (A[0]+height*sina, y1 - height/2+missiled.get_height())
if -180<-fangle<-90:
A = (x1-width-height*sina, y1 - height/2+missiled.get_height())
B = (x1 - width,A[1]+height*cosa )
C = ((A[0] + B[0]) / 2, (A[1] + B[1]) / 2)
screen.fill((0,0,0))
screen.blit(missiled, (x1-width+(x1-C[0]),y1-height/2+(y1-C[1])))
screen.blit(textc, (x,y)) #鼠标用一个红色*代替
pygame.display.update()

以上便是用Python模拟导弹自动追踪的代码实例。

Atas ialah kandungan terperinci Gunakan Python untuk melaksanakan pengesanan automatik peluru berpandu, sangat terbakar!. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!