java各种排序算法及实现
- 阿神asal
- 2016-11-07 17:53:462055semak imbas
先来看看8种排序之间的关系:
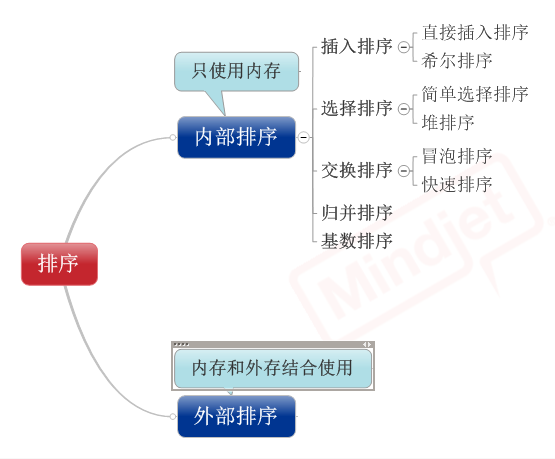
下图是各种排序的比较:
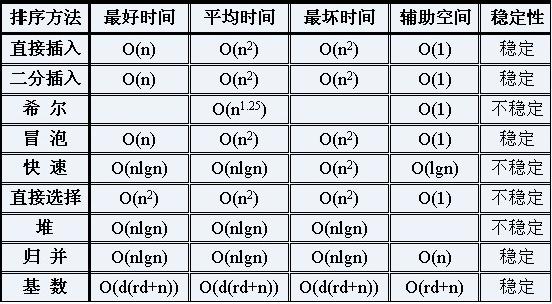
1, 直接插入排序
(1)基本思想:在要排序的一组数中,假设前面(n-1) [n>=2] 个数已经是排
好顺序的,现在要把第n个数插到前面的有序数中,使得这n个数
也是排好顺序的。如此反复循环,直到全部排好顺序。
在插入算法中,如果有一个最小的数在数组的最后面,用插入算法就会从最后一个
位置移动到第一个。
(2)实例
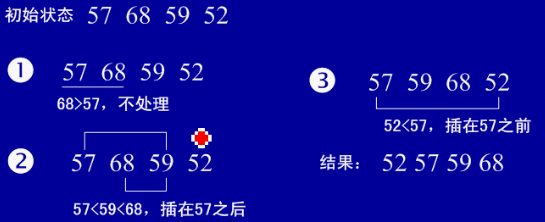
package cglib;
public class StringNumber {
public static void insertSort(int[] a) {
if (a == null || a.length < 2) {
return;
}
int length=a.length; //数组长度
int j; //当前值的位置
int i; //指向j前的位置
int key; //当前要进行插入排序的值
//从数组的第二个位置开始遍历值
for(j=1;j<length;j++){
key=a[j];
i=j-1;
System.out.println(" 将i="+i);
//a[i]比当前值大时,a[i]后移一位,空出i的位置,好让下一次循环的值后移
while(i>=0 && a[i]>key){
System.out.println("进 i="+i);
a[i+1]=a[i]; //将a[i]值后移
i--; //i前移
System.out.println(" i="+i);
}//跳出循环(找到要插入的中间位置或已遍历到0下标)
System.out.println(" 退出while");
System.out.println(" i="+i);
a[i+1]=key; //将当前值插入
}
}
public static void main(String[] args) {
int[] array = { 3, -1, 0, -8, 2, 1 };
ArrayUtils.printArray(array);
insertSort(array);
ArrayUtils.printArray(array);
}
}
class ArrayUtils {
public static void printArray(int[] array) {
System.out.print("{");
for (int i = 0; i < array.length; i++) {
System.out.print(array[i]);
if (i < array.length - 1) {
System.out.print(", ");
}
}
System.out.println("}");
}
} 输出:
{3, -1, 0, -8, 2, 1}
将i=0
进 i=0
i=-1
退出while
i=-1
将i=1
进 i=1
i=0
退出while
i=0
将i=2
进 i=2
i=1
进 i=1
i=0
进 i=0
i=-1
退出while
i=-1
将i=3
进 i=3
i=2
退出while
i=2
将i=4
进 i=4
i=3
进 i=3
i=2
退出while
i=2
{-8, -1, 0, 1, 2, 3}希尔排序(最小增量排序)
基本算法:
先将整个待排元素序列分割成若干个子序列(由相隔某个“增量”的元素组成的)分别进行直接插入排序,然后依次缩减增量再进行排序,待整个序列中的元 素基本有序(增量足够小)时,再对全体元素进行一次直接插入排序。因为直接插入排序在元素基本有序的情况下(接近最好情况),效率是很高的,因此希尔排序在时间效率上比前两种方法有较大提高。步长的选择是希尔排序的重要部分。只要最终步长为1任何步长序列都可以工作。
算法最开始以一定的步长进行排序,然后会继续以一定步长进行排序,最终算法以步长为1进行排序。当步长为1时,算法变为插入排序,这就保证了数据一 定会被排序。Donald Shell 最初建议步长选择为\frac{n}{2}并且对步长取半直到步长达到 1。虽然这样取可以比\mathcal{O}(n^2)类的算法(插入排序)更好,但这样仍然有减少平均时间和最差时间的余地。
希尔排序示例:n=10的一个数组 58 27 32 93 65 87 58 46 9 65,步长为n/2。
第一次排序 步长为 10/2 = 5
58 27 32 93 65 87 58 46 9 65
1A 1B
2A 2B
3A 3B
4A 4B
5A 5B
首先将待排序元素序列分组,以5为步长,(1A,1B), (2A,2B),(3A,3B)等为分组标记,大写字母表示是该组的第几个元素,数字相同的表示在同一组,这样就分成5组,即(58,87), (27,58),(32,46),(93,9),(65,65),然后分别对各分组进行直接插入排序,排序后5组为(58,87),(27,58), (32,46),(9,93),(65,65),分组排序只是变得各个分组内的下表,下同。
第二次排序 步长为 5/2 = 2
58 27 32 9 65 87 58 46 93 65
1A 1B
2A 2B
3A 3B
.............................................
第三次排序 步长为 2/2 = 1
32 9 58 27 58 46 65 65 93 87
1A 1B 1C 1D 1E 1F 1G 1H 1I 1J
第四次排序 步长为 1/2 = 0 得到有序元素序列
9 27 32 46 58 58 65 65 87 93
希尔排序的时间性能优于直接插入排序的原因:
①当文件初态基本有序时直接插入排序所需的比较和移动次数均较少。
②当n值较小时,n和n2的差别也较小,即直接插入排序的最好时间复杂度O(n)和最坏时间复杂度0(n2)差别不大。
③在希尔排序开始时增量较大,分组较多,每组的记录数目少,故各组内直接插入较快,后来增量di逐渐缩小,分组数逐渐减少,而各组的记录数目逐渐增多,但由于已经按di-1作为距离排过序,使文件较接近于有序状态,所以新的一趟排序过程也较快。
增量序列的选择:Shell排序的执行时间依赖于增量序列。
好的增量序列的共同特征(查到的资料都这么讲):
① 最后一个增量必须为1;
② 应该尽量避免序列中的值(尤其是相邻的值)互为倍数的情况。
package cglib;
public class StringNumber {
public static void main(String[] args) {
int[] arr = new int[]{44,33,99,10,30,20,59,78,23,48};
System.out.print("排序前:");
for(int o: arr) {
System.out.print(o+" ");
}
System.out.println();
shellSort(arr);
System.out.print("排序后:");
for(int o: arr) {
System.out.print(o+" ");
}
System.out.println();
}
private static void shellSort(int[] arr) {
int j;
int len = arr.length;
for(int val=len>>1; val>0; val>>=1) {
//下面是对本次的所有分组做直接插入排序
for(int i=val; i<len; i++) {
System.out.println("for:i="+i);
System.out.println("for:arr[i]="+arr[i]);
System.out.println("for:val="+val);
int temp = arr[i];
/*
* 为什么每次都用temp比较呢?
* 因为直接插入就是找到temp的合适位置。
* 为什么temp<arr[j-val]这个条件可以放在for内呢?
* 因为原来的组内数据已经有序,找到位置就停止便是。
*
*/
for(j=i; j>=val&&temp<arr[j-val]; j-=val) {
System.out.println("er:j="+j);
System.out.println("er:arr[j]="+arr[j]);
System.out.println("er:j-val="+(j-val));
System.out.println("er:arr[j-val]="+arr[j-val]);
/*
* 为什么是arr[j-val]不是arr[j]呢?
* 因为j=i开始的,而且条件是j>=val&&temp<arr[j-val]
*/
arr[j] = arr[j-val];
System.out.println("赋值er:arr[j]="+arr[j]);
}
/*
* 注意不是arr[i] = temp
* 直接插入排序也是这样的。
* 为什么呢?
* 因为j是位置,i是待插入元素
*/
arr[j] = temp;
}
}
}
}输出:
排序前:44 33 99 10 30 20 59 78 23 48 for:i=5 for:arr[i]=20 for:val=5 er:j=5 er:arr[j]=20 er:j-val=0 er:arr[j-val]=44 赋值er:arr[j]=44 for:i=6 for:arr[i]=59 for:val=5 for:i=7 for:arr[i]=78 for:val=5 er:j=7 er:arr[j]=78 er:j-val=2 er:arr[j-val]=99 赋值er:arr[j]=99 for:i=8 for:arr[i]=23 for:val=5 for:i=9 for:arr[i]=48 for:val=5 for:i=2 for:arr[i]=78 for:val=2 for:i=3 for:arr[i]=10 for:val=2 er:j=3 er:arr[j]=10 er:j-val=1 er:arr[j-val]=33 赋值er:arr[j]=33 for:i=4 for:arr[i]=30 for:val=2 er:j=4 er:arr[j]=30 er:j-val=2 er:arr[j-val]=78 赋值er:arr[j]=78 for:i=5 for:arr[i]=44 for:val=2 for:i=6 for:arr[i]=59 for:val=2 er:j=6 er:arr[j]=59 er:j-val=4 er:arr[j-val]=78 赋值er:arr[j]=78 for:i=7 for:arr[i]=99 for:val=2 for:i=8 for:arr[i]=23 for:val=2 er:j=8 er:arr[j]=23 er:j-val=6 er:arr[j-val]=78 赋值er:arr[j]=78 er:j=6 er:arr[j]=78 er:j-val=4 er:arr[j-val]=59 赋值er:arr[j]=59 er:j=4 er:arr[j]=59 er:j-val=2 er:arr[j-val]=30 赋值er:arr[j]=30 for:i=9 for:arr[i]=48 for:val=2 er:j=9 er:arr[j]=48 er:j-val=7 er:arr[j-val]=99 赋值er:arr[j]=99 for:i=1 for:arr[i]=10 for:val=1 er:j=1 er:arr[j]=10 er:j-val=0 er:arr[j-val]=20 赋值er:arr[j]=20 for:i=2 for:arr[i]=23 for:val=1 for:i=3 for:arr[i]=33 for:val=1 for:i=4 for:arr[i]=30 for:val=1 er:j=4 er:arr[j]=30 er:j-val=3 er:arr[j-val]=33 赋值er:arr[j]=33 for:i=5 for:arr[i]=44 for:val=1 for:i=6 for:arr[i]=59 for:val=1 for:i=7 for:arr[i]=48 for:val=1 er:j=7 er:arr[j]=48 er:j-val=6 er:arr[j-val]=59 赋值er:arr[j]=59 for:i=8 for:arr[i]=78 for:val=1 for:i=9 for:arr[i]=99 for:val=1 排序后:10 20 23 30 33 44 48 59 78 99
选择排序
每一趟从待排序的数据元素中选出最小(或最大)的一个元素,顺序放在已排好序的数列的最后,直到全部待排序的数据元素排完。
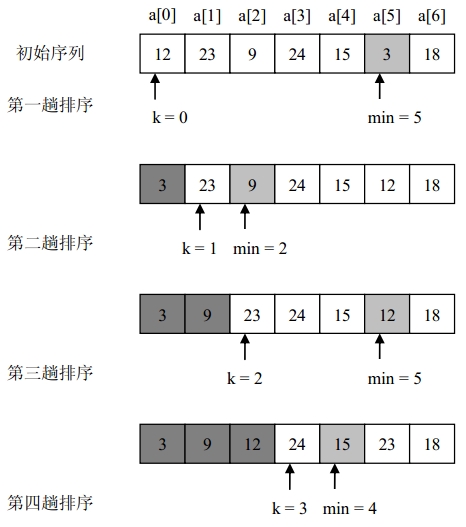
package cglib;
import java.util.Arrays;
import java.util.Date;
import java.util.Random;
public class StringNumber {
public static void main(String[] args){
Random random = new Random();
int[] array = new int[2000];
for (int j = 0; j < 2000; j++) {
array[j] = random.nextInt(100000);
}
System.out.println(Arrays.toString(array));
selectSortTest(array);
System.out.println(Arrays.toString(array));
}
public static void selectSortTest(int a[]) {
Date dateStart = new Date();
selectSort(a);
Date dateEnd = new Date();
System.out.println("选择排序耗费时间:"
+ (dateEnd.getTime() - dateStart.getTime()));
}
public static void selectSort(int a[]){
int n = a.length;
for(int k=0; k<n-1; k++) {
int min = k;
for(int i=k+1; i<n; i++) {//找出最小值
if(a[i] < a[min]) {
min = i;
}
}
if(k != min) {
int temp = a[k];
a[k] = a[min];
a[min] = temp;
}
}
}
}
