Mengalahkan Kemungkinan: Matematik di Sebalik Keuntungan Kasino

Pernahkah anda terfikir mengapa kasino kelihatan sentiasa menang? Dalam “Beating the Odds: The Mathematics Behind Behind Casino Profit,” kami akan meneroka matematik mudah dan strategi pintar yang memastikan kasino menjana wang dalam jangka masa panjang. Melalui contoh yang mudah difahami dan simulasi Monte Carlo, kami akan mendedahkan rahsia di sebalik tepi rumah. Bersedia untuk mengetahui cara kasino mengubah peluang memihak kepada mereka!

Memahami Tepi Rumah

Pinggir rumah ialah konsep asas dalam dunia kasino. Ia mewakili purata keuntungan yang kasino jangkakan untuk membuat daripada setiap pertaruhan yang diletakkan oleh pemain. Pada asasnya, ia adalah peratusan setiap pertaruhan yang kasino akan kekalkan dalam jangka masa panjang.

Pinggiran rumah wujud kerana kasino tidak membayar pertaruhan yang menang mengikut "kemungkinan sebenar" permainan. Peluang sebenar mewakili kebarangkalian sebenar sesuatu peristiwa berlaku. Dengan membayar pada kemungkinan yang lebih rendah sedikit, kasino memastikan mereka memperoleh keuntungan dari semasa ke semasa.

Tepi rumah (HE) ditakrifkan sebagai keuntungan kasino yang dinyatakan sebagai peratusan daripada pertaruhan asal pemain.

** European Roulette ** hanya mempunyai satu sifar hijau, memberikannya 37 nombor secara keseluruhan. Jika pemain bertaruh $1 pada merah, mereka mempunyai peluang 18/37 untuk memenangi $1 dan peluang 19/37 untuk kehilangan $1. Nilai yang dijangkakan ialah:

Nilai Jangkaan=( 1 × 18/37 ​)+( −1 × 19/37 ​)= 18/37​ − 19/37​ = −1/37 ​≈ −2.7%

Oleh itu, Dalam Roulette Eropah, tepi rumah(HE) adalah sekitar 2.7%.

Mari kita buat permainan kita sendiri untuk memahaminya dengan lebih mendalam, Permainan guling Dadu Mudah.

import random

def roll_dice():
    roll = random.randint(1, 100)

    if roll == 100:
        print(roll, 'You rolled a 100 and lost. Better luck next time!')
        return False
    elif roll <= 50:
        print(roll, 'You rolled between 1 and 50 and lost.')
        return False
    else:
        print(roll, 'You rolled between 51 and 99 and won! Keep playing!')
        return True

Dalam permainan ini:

• Pemain mempunyai peluang 1/100 untuk kalah jika senarai 100.

• Pemain mempunyai peluang 50/100 untuk kalah jika pusingan antara 1 dan 50.

• Pemain mempunyai peluang 49/100 untuk menang jika senarai antara 51 dan 99.

Nilai Jangkaan =(1× 49/100​) + ( −1× 51/100​) = 49/100​ − 51/100 ​= −2/100 ​ ≈ −2%

Oleh itu, tepi rumah adalah 2%.

Memahami Simulasi Monte Carlo

Simulasi Monte Carlo ialah alat berkuasa yang digunakan untuk memahami dan meramal sistem yang kompleks dengan menjalankan pelbagai simulasi proses dan memerhatikan hasilnya. Dalam konteks kasino, simulasi Monte Carlo boleh memodelkan pelbagai senario pertaruhan untuk menunjukkan bagaimana kelebihan rumah memastikan keuntungan jangka panjang. Mari terokai cara simulasi Monte Carlo berfungsi dan cara ia boleh digunakan pada permainan kasino yang mudah.

Apakah Simulasi Monte Carlo?

Simulasi Monte Carlo melibatkan penjanaan pembolehubah rawak untuk mensimulasikan proses beberapa kali dan menganalisis keputusan. Dengan melakukan beribu-ribu malah berjuta-juta lelaran, kami boleh memperoleh pengedaran hasil yang mungkin dan mendapatkan cerapan tentang kemungkinan peristiwa yang berbeza.

Mengaplikasikan Simulasi Monte Carlo pada Permainan Guling Dadu

Kami akan menggunakan simulasi Monte Carlo untuk memodelkan permainan balingan dadu yang telah dibincangkan sebelum ini. Ini akan membantu kami memahami cara kelebihan rumah mempengaruhi keuntungan permainan dari semasa ke semasa.

`def monte_carlo_simulation(trials):
    wins = 0
    losses = 0

    for _ in range(trials):
        if roll_dice():
            wins += 1
        else:
            losses += 1

    win_percentage = (wins / trials) * 100
    loss_percentage = (losses / trials) * 100
    houseEdge= loss_percentage-win_percentage
    print(f"After {trials} trials:")
    print(f"Win percentage: {win_percentage:.2f}%")
    print(f"Loss percentage: {loss_percentage:.2f}%")
    print(f"House Edge: {houseEdge:.2f}%")

# Run the simulation with 10,000,000 trials
monte_carlo_simulation(10000000)`

Mentafsir Keputusan

Dalam simulasi ini, kami menjalankan permainan membaling dadu sebanyak 10,000,000 kali untuk memerhatikan peratusan menang dan kalah. Memandangkan kelebihan rumah yang dikira lebih awal (2%), kami menjangkakan peratusan kerugian akan lebih tinggi sedikit daripada peratusan kemenangan.

Selepas menjalankan simulasi, anda mungkin melihat hasil seperti:

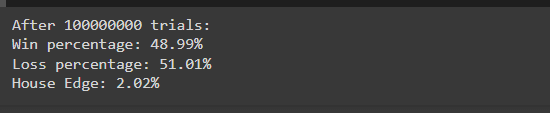
Keputusan ini sejajar rapat dengan kebarangkalian teori (49% menang, 51% kalah), menunjukkan cara kelebihan rumah ditunjukkan dalam sejumlah besar percubaan. Ketidakseimbangan yang sedikit memastikan keuntungan kasino dalam jangka panjang.

Menggambarkan Kemenangan Jangka Pendek dan Kerugian Jangka Panjang

Simulasi Monte Carlo berkuasa untuk memodelkan dan meramalkan hasil melalui persampelan rawak berulang. Dalam konteks perjudian, kami boleh menggunakan simulasi Monte Carlo untuk memahami potensi hasil strategi pertaruhan yang berbeza.

Kami akan mensimulasikan seorang pertaruhan yang meletakkan pertaruhan awal yang sama dalam setiap pusingan dan memerhatikan bagaimana nilai akaun mereka berkembang mengikut bilangan pertaruhan yang ditentukan.

Begini cara kami boleh mensimulasikan dan menggambarkan perjalanan pertaruhan menggunakan Matplotlib:

def bettor_simulation(funds, initial_wager, wager_count):
    value = funds
    wager = initial_wager

    # Lists to store wager count and account value
    wX = []
    vY = []

    current_wager = 1

    while current_wager <= wager_count:
        if roll_dice():
            value += wager
        else:
            value -= wager

        wX.append(current_wager)
        vY.append(value)
        current_wager += 1

    return wX, vY

# Parameters for simulation
funds = 10000
initial_wager = 100
wager_count = 1000

# Run the simulation for a single bettor
wager_counts, account_values = bettor_simulation(funds, initial_wager, wager_count)

# Plotting the results
plt.figure(figsize=(12, 6))
plt.plot(wager_counts, account_values, label='Bettor 1', color='blue')
plt.xlabel('Wager Count')
plt.ylabel('Account Value')
plt.title('Betting Journey: Short-Term Wins vs Long-Term Losses')
plt.grid(True)
plt.legend()

# Highlighting the short-term and long-term trend
plt.axhline(y=funds, color='gray', linestyle='--', label='Initial Funds')
plt.axhline(y=account_values[0], color='green', linestyle='--', label='Starting Account Value')
plt.axhline(y=account_values[-1], color='red', linestyle='--', label='Final Account Value')

plt.legend()
plt.show()

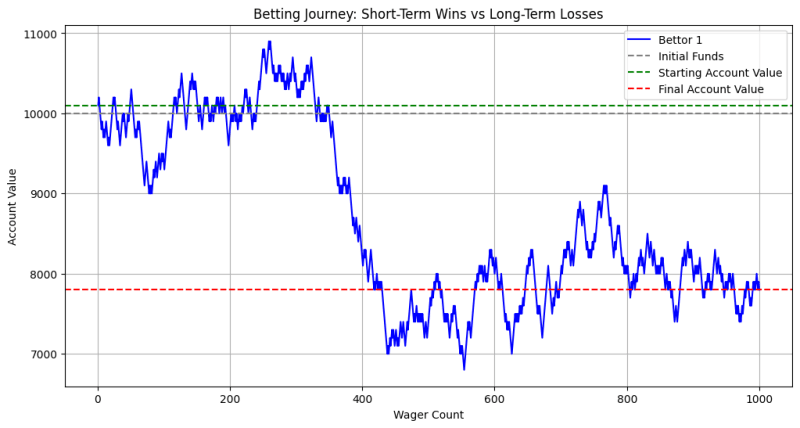
Graf ini menggambarkan bagaimana nilai akaun petaruh boleh berubah-ubah dari semasa ke semasa disebabkan oleh kemenangan dan kerugian. Pada mulanya, mungkin terdapat tempoh kemenangan (garisan hijau di atas nilai permulaan), tetapi apabila bilangan taruhan meningkat, kesan kumulatif kelebihan rumah menjadi jelas. Akhirnya, nilai akaun pertaruhan cenderung menurun ke arah atau di bawah dana awal (garis kelabu), menunjukkan kerugian jangka panjang.

Kesimpulan

Memahami matematik di sebalik keuntungan kasino mendedahkan kelebihan yang jelas untuk rumah dalam setiap permainan melalui konsep tepi rumah. Walaupun menang sekali-sekala, kebarangkalian yang dibina dalam permainan kasino memastikan kebanyakan pemain akan kehilangan wang dari semasa ke semasa. Simulasi Monte Carlo jelas menggambarkan dinamik ini, menunjukkan bagaimana walaupun kemenangan jangka pendek boleh menutup kerugian jangka panjang disebabkan kelebihan statistik kasino. Pemahaman tentang kepastian matematik keuntungan kasino ini menekankan kepentingan membuat keputusan termaklum dan amalan perjudian yang bertanggungjawab.

Seterusnya, kita boleh meneroka visualisasi atau variasi tambahan, seperti membandingkan strategi pertaruhan yang berbeza atau menganalisis kesan pertaruhan awal yang berbeza-beza terhadap hasil petaruh.

Kekal Berhubung:

• GitHub: ezhillragesh

• Twitter: ezhillragesh

• Laman web: ragesh.me

Jangan teragak-agak untuk berkongsi pendapat anda, bertanya soalan dan menyumbang kepada perbincangan.

Selamat mengekod!

Atas ialah kandungan terperinci Mengalahkan Kemungkinan: Matematik di Sebalik Keuntungan Kasino. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!