1차 최적화 알고리즘에서 영감을 받아 Peking University Lin Zhouchen 팀은 보편적 근사 속성을 갖춘 신경망 아키텍처의 설계 방법을 제안했습니다.

딥러닝 기술의 기반이 되는 신경망은 다양한 응용 분야에서 효과적인 결과를 얻었습니다. 실제로 네트워크 아키텍처는 학습 효율성에 큰 영향을 미칠 수 있습니다. 좋은 신경망 아키텍처는 문제에 대한 사전 지식을 통합하고 네트워크 교육을 설정하며 컴퓨팅 효율성을 향상시킬 수 있습니다. 현재 고전적인 네트워크 아키텍처 설계 방법에는 수동 설계, 신경망 아키텍처 검색(NAS)[1], 최적화 기반 네트워크 설계 방법[2]이 포함됩니다. ResNet 등과 같은 인공적으로 설계된 네트워크 아키텍처, 검색 또는 강화 학습을 통해 검색 공간에서 최상의 네트워크 구조를 검색합니다. 최적화 기반 설계 방법의 주류 패러다임은 일반적으로 이 방법이 네트워크를 설계합니다. 명시적 목적 함수를 사용하는 최적화 알고리즘의 관점에서 구조를 설명합니다. 이들 방법은 최적화 알고리즘 관점에서 네트워크 구조를 설계하고, 최적화 알고리즘 관점에서 네트워크 구조를 설계한다.

요즘 대부분의 고전적인 신경망 아키텍처 설계는 네트워크의 보편적인 근사치를 무시합니다. 이는 신경망의 강력한 성능을 위한 핵심 요소 중 하나입니다. 따라서 이러한 설계 방법은 네트워크의 사전 성능 보장을 어느 정도 상실합니다. 2계층 신경망은 너비가 무한대에 가까워질 때 보편적인 근사 특성을 가지지만[3] 실제로는 일반적으로 너비가 제한된 네트워크 구조만 고려할 수 있으며 이 영역의 성능 분석 결과는 매우 제한적입니다. 실제로, 휴리스틱 인공 설계이든 블랙박스 신경망 아키텍처 검색이든 네트워크 설계에서는 보편적인 근사 속성을 고려하기가 어렵습니다. 최적화 기반 신경망 설계는 상대적으로 해석하기가 더 쉽지만 일반적으로 명확한 목적 함수가 필요하므로 설계되는 네트워크 구조의 다양성이 제한되고 적용 범위가 제한됩니다. 보편적인 근사 속성을 갖춘 신경망 아키텍처를 체계적으로 설계하는 방법은 여전히 ​​중요한 문제로 남아 있습니다.

북경대학교 Lin Zhouchen 교수팀은 최적화 알고리즘 설계 도구를 기반으로 하는 신경망 아키텍처를 제안했습니다. 이 방법은 경사 기반 1차 최적화 알고리즘과 해시 기반 2차 최적화 알고리즘을 결합하여 훈련 속도를 향상시킵니다. 최적화 알고리즘과 수렴 성능을 향상하고 신경망의 견고성을 보장합니다. 이 신경망 모듈은 기존의 모듈화 기반 네트워크 설계 방법과도 함께 사용할 수 있으며 모델 성능을 지속적으로 향상시킵니다. 최근에는 신경망 미분 방정식(NODE)의 근사 속성을 분석하고, 교차 계층 연결 신경망이 보편적 근사 속성을 가짐을 증명했으며, 또한 제안한 프레임워크를 사용하여 ConvNext 및 ViT와 같은 변형 네트워크를 설계하고 결과를 얻었습니다. 기준치를 초과한 것입니다. 해당 논문은 인공지능 분야 최고 저널인 TPAMI에 게재됐다.

• 논문: 보편적으로 근사하는 심층 신경망 설계: 1차 최적화 접근 방식
• 논문 주소: https://ieeexplore.ieee.org/document/10477580

방법 소개

전통적인 최적화 기반 신경망 설계 방법은 명시적인 표현을 사용하는 목적 함수에서 시작하여 특정 최적화 알고리즘을 사용하여 이를 해결한 다음 최적화 결과를 유명한 LISTA와 같은 신경망 구조에 매핑하는 경우가 많습니다. - NN은 LASSO 문제를 해결하기 위해 LISTA 알고리즘을 사용하여 얻은 명시적 표현으로, 최적화 결과를 신경망 구조로 변환한다[4]. 이 방법은 목적함수의 명시적 표현에 대한 의존도가 높기 때문에 결과 네트워크 구조는 목적함수의 명시적 표현에만 최적화될 수 있으며 실제 상황에 맞지 않는 가정을 설계할 위험이 있습니다. 일부 연구자들은 목적 함수를 맞춤화한 후 알고리즘 확장 등의 방법을 사용하여 네트워크 구조를 설계하려고 시도하지만 실제 상황에서는 가정을 반드시 충족하지 못할 수 있는 가중치 리바인딩과 같은 가정도 필요합니다. 따라서 일부 연구자들은 보다 합리적인 네트워크 구조를 얻기 위해 신경망 기반의 진화 알고리즘을 사용하여 네트워크 아키텍처를 검색할 것을 제안했습니다.

업데이트된 네트워크 아키텍처 설계 계획의 형식은 1차 최적화 알고리즘부터 더 가까운 지점 알고리즘까지의 아이디어를 따르고 점진적인 최적화를 수행해야 합니다. 예를 들어, 오일러 각도 알고리즘을 쿼터니언 알고리즘으로 변경하거나 보다 효율적인 반복 알고리즘을 사용하여 솔루션을 근사화할 수 있습니다. 업데이트된 형식은 계산 정확도를 높이고 운영 효율성을 향상시키는 것을 고려해야 합니다.

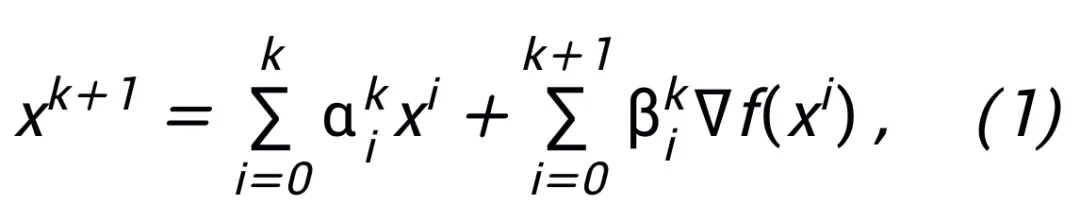
여기서 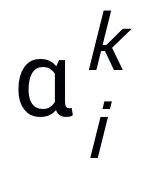및 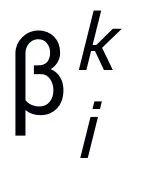는 k번째 단계 업데이트의 (단계 크기) 계수를 나타내고, 그런 다음 기울기 항을 신경망의 학습 가능한 모듈 T로 대체하여 L 계층 신경망의 골격을 얻습니다.

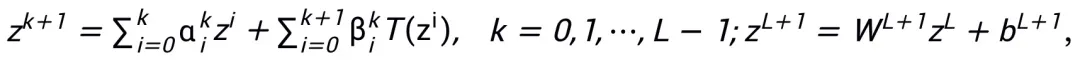
전체 메서드 프레임워크는 그림 1에 나와 있습니다.

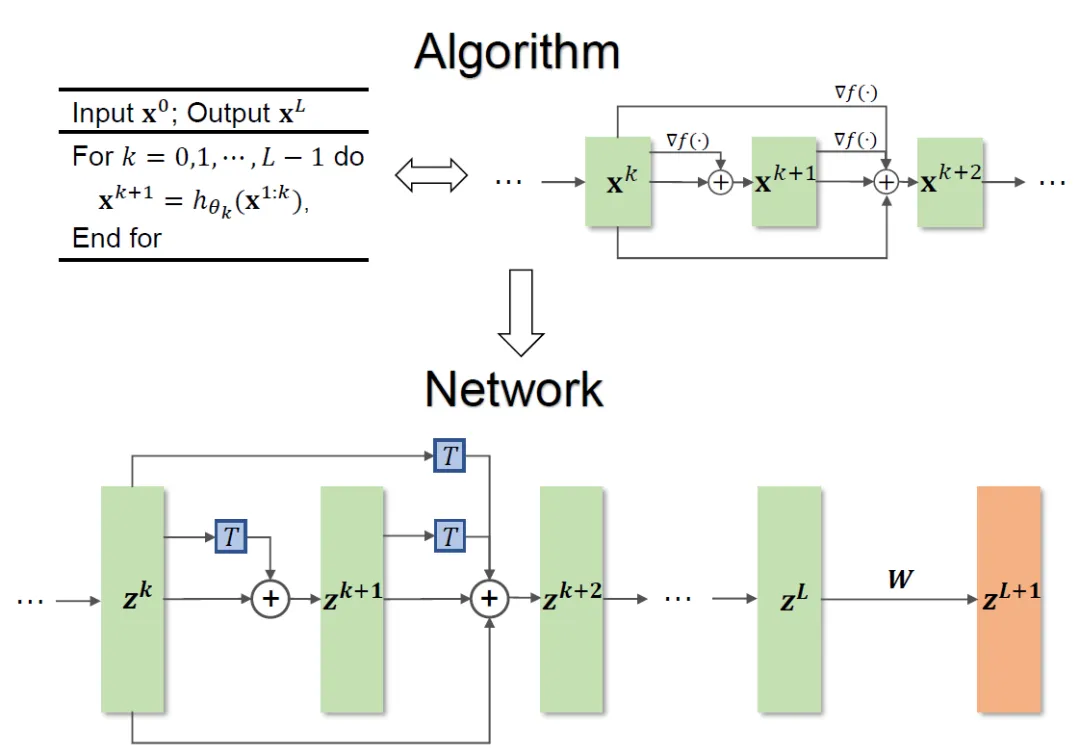
그림 1 네트워크 설계 그림

논문에서 제안된 방법은 ResNet 및 DenseNet과 같은 기존 네트워크의 설계에 영감을 줄 수 있으며, 네트워크 아키텍처 설계의 최적화를 기반으로 하는 기존 방법의 문제를 해결합니다. 특정 목적 함수로 제한됩니다.

모듈 선택 및 아키텍처 세부 사항

이 방법으로 설계된 네트워크 모듈 T는 하위 구조로 2계층 네트워크 구조, 즉 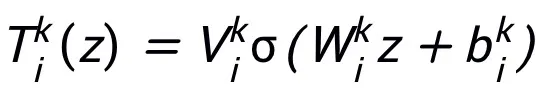만 필요하므로 설계된 네트워크가 표현되는 레이어의 너비가 제한되어 (즉, 근사 정확도가 향상되어도 커지지 않음)하는 보편적 근사 속성을 가지며, 을 넓혀도 전체 네트워크의 보편적 근사 속성을 얻지 못합니다. 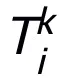레이어. 모듈 T는 ResNet에서 널리 사용되는 사전 활성화 블록일 수도 있고 Transformer의 Attention + Feedforward 레이어 구조일 수도 있습니다. T의 활성화 함수는 ReLU, GeLU, Sigmoid 등과 같은 일반적인 활성화 함수일 수 있습니다. 특정 작업에 따라 해당 정규화 레이어를 추가할 수도 있습니다. 또한 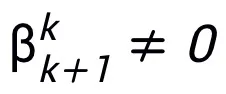인 경우 설계된 네트워크는 암시적 네트워크[5]이며 고정 소수점 반복 방법을 사용하여 암시적 형식을 근사화하거나 암시적 미분 방법을 사용하여 업데이트를 위한 기울기를 해결할 수 있습니다.

등가 표현을 통해 더 많은 네트워크 설계

이 방법은 동일한 알고리즘이 하나의 구조에만 대응할 수 있도록 요구하지 않습니다. 반대로 이 방법은 최적화 문제의 등가 표현을 사용하여 더 많은 네트워크를 설계할 수 있습니다. 유연성을 반영하는 아키텍처. 예를 들어, 선형화된 교번 방향 곱셈기 방법은 제한된 최적화 문제를 해결하는 데 자주 사용됩니다. 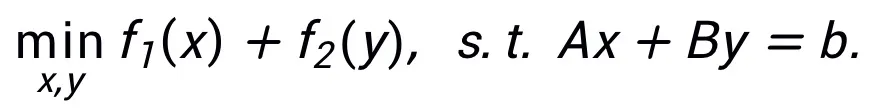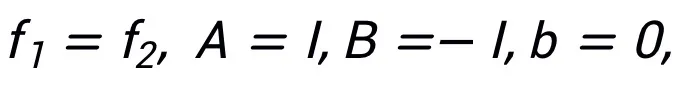을 허용하면 네트워크에 영감을 줄 수 있는 업데이트된 반복 형식을 얻을 수 있습니다.

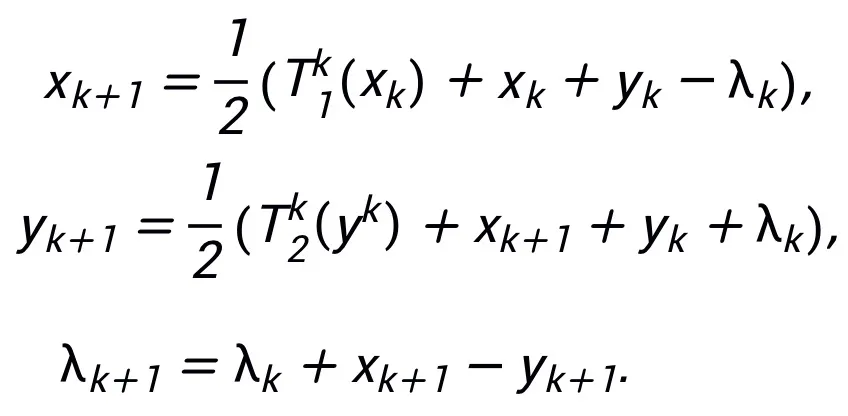
네트워크 구조는 영감을 받은 그림 2를 참조하세요.

그림 2 선형 교번 방향 곱셈 방법에서 영감을 받은 네트워크 구조

영감받은 네트워크는 보편적 근사 속성을 가집니다

이 방법으로 설계된 네트워크 아키텍처는 모듈이 이전 조건을 충족하고 (일반적으로) 최적화 알고리즘이 안정적이고 수렴하는 조건에서 1차 최적화 알고리즘에서 영감을 받은 신경망이 다음을 갖는다는 것을 증명할 수 있습니다. 고차원 연속함수 공간의 특성 모든 근사 속성이 주어지고, 근사 속도가 주어진다. 이 논문은 처음으로 제한된 너비 설정에서 일반적인 교차 계층 연결을 사용하는 신경망의 보편적인 근사 속성을 증명했습니다(이전 연구는 기본적으로 FCNN 및 ResNet에 중점을 두었습니다. 논문의 주요 정리는 다음과 같습니다).

주요 정리(짧은 버전): 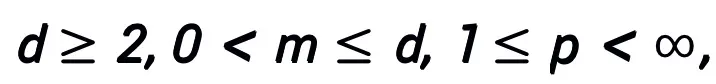A을 그라디언트 1차 최적화 알고리즘이라고 가정합니다. 알고리즘 A가 식 (1)의 업데이트 형식을 갖고 수렴 조건을 만족하는 경우(최적화 알고리즘에 대한 공통 단계 크기 선택은 모두 수렴 조건을 만족합니다. 모두 휴리스틱 네트워크에서 학습 가능한 경우 이 조건은 필요하지 않습니다), 신경 알고리즘에서 영감을 받은 네트워크:

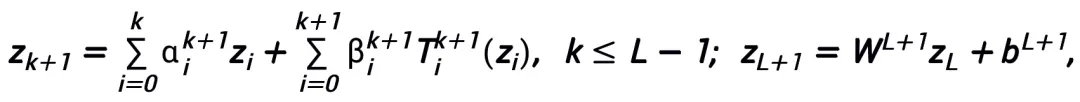
은 연속(벡터 값) 함수 공간 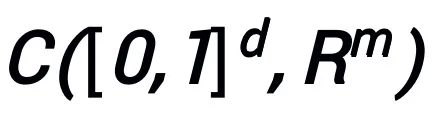및 표준 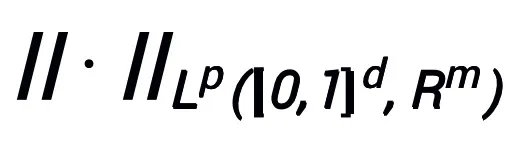에서 보편적인 근사 속성을 가집니다. 여기서 학습 가능한 모듈 T는 두 개의 A 구조만 포함하면 됩니다. (σ는 일반적으로 사용되는 활성화 함수일 수 있음)과 같은 레이어 모양을 해당 하위 구조로 사용할 수 있습니다.

일반적으로 사용되는 T 구조는 다음과 같습니다.

1) Convolutional 네트워크에서 사전 활성화 블록: BN-ReLU-Conv-BN-ReLU-Conv (z),

2) Transformer에서: Attn (z) + MLP (z+Attn (z)) 주 정리의 증명은 NODE의 보편적 근사 속성과 선형 다단계 방법의 수렴 속성을 활용하는 것입니다. 최적화 알고리즘 설계는 수렴 선형 다단계 방법에 의한 연속 NODE의 이산화에 해당하므로 영감을 받은 네트워크는 NODE의 근사 능력을 "상속"합니다. 증명에서 논문은 또한 d차원 공간에서 연속 함수를 근사화하기 위한 NODE의 근사 속도를 제공하여 이전 논문의 나머지 문제를 해결합니다[6].

표 1 기본적으로 FCNN과 ResNet에 초점을 맞춘 보편 근사 속성에 대한 이전 연구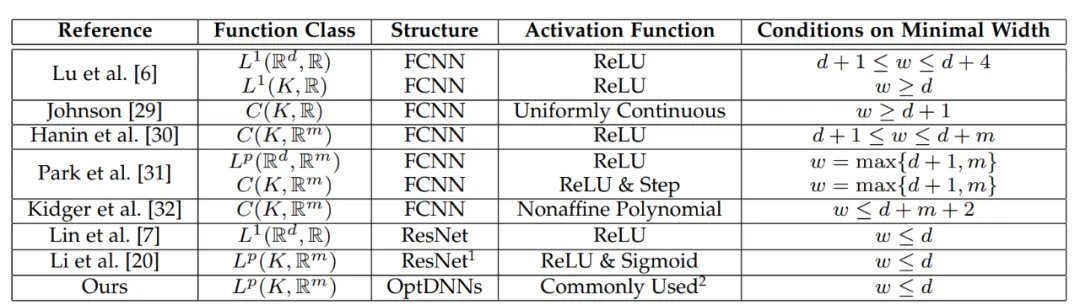

실험 결과

논문에서는 제안된 네트워크 아키텍처 설계 프레임워크를 사용하여 8개의 명시적 네트워크와 3개의 암시적 네트워크를 설계했습니다. (OptDNN이라고 함) 네트워크 정보는 표 2와 같으며 중첩된 링 분리, 함수 근사화 및 이미지 분류와 같은 문제에 대한 실험을 수행했습니다. 또한 본 논문에서는 ResNet, DenseNet, ConvNext 및 ViT를 기준선으로 사용하고, 제안된 방법을 사용하여 개선된 OptDNN을 설계하고, 두 가지 정확도 지표와 FLOP를 고려하여 이미지 분류 문제에 대한 실험을 수행합니다.

표 2 설계된 네트워크 관련 정보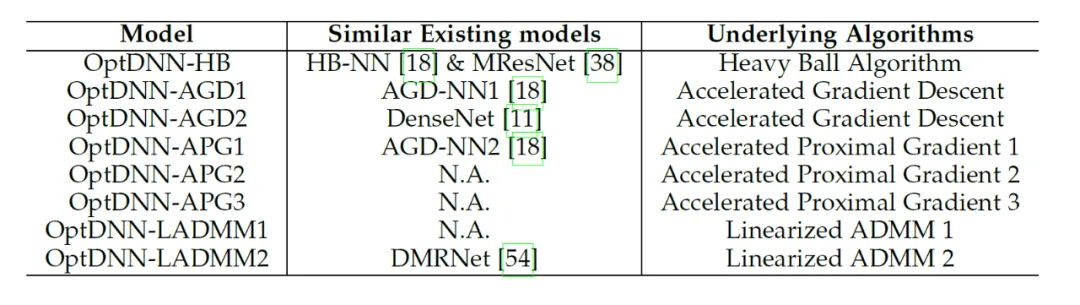

먼저 OptDNN은 중첩 링 분리와 함수 근사라는 두 가지 문제에 대한 실험을 수행하여 보편 근사 속성을 검증합니다. 함수 근사 문제에서는 근사 패리티 함수와 Talgarsky 함수를 각각 고려합니다. 전자는 이진 분류 문제로 표현될 수 있고, 후자는 회귀 문제로 얕은 네트워크로는 근사가 어렵습니다. 중첩된 링 분리에서 OptDNN의 실험 결과는 그림 3에 나와 있으며, 함수 근사에 대한 실험 결과는 그림 3에 나와 있습니다. OptDNN은 좋은 분리/근사 결과를 얻었을 뿐만 아니라 기준선인 ResNet보다 더 큰 결과를 얻었습니다. 분류 간격과 더 작은 회귀 오류는 OptDNN의 보편적인 근사 속성을 검증하는 데 충분합니다.

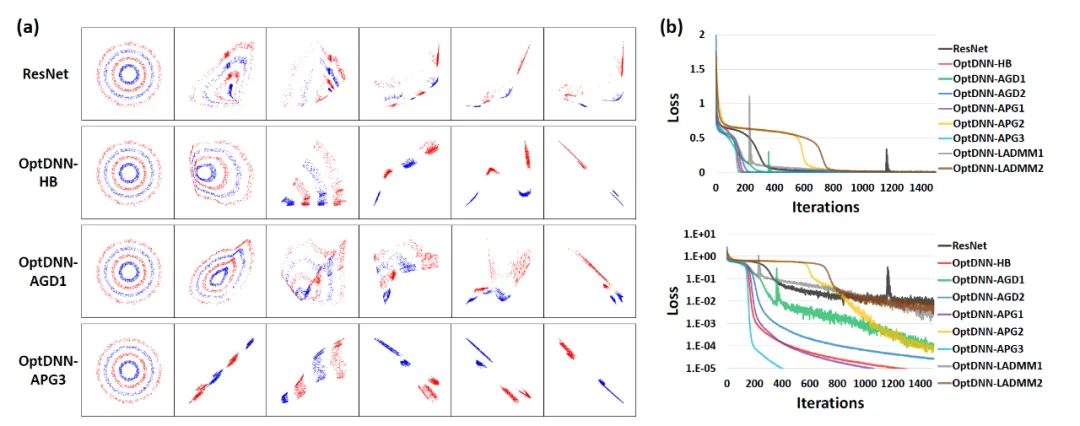
그림 3 패리티 함수를 근사화하는 OptNN

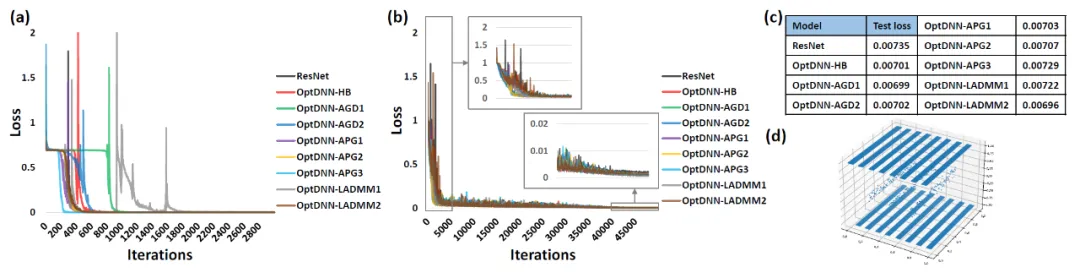
그림 4 Talgarsky 함수를 근사화하는 OptNN

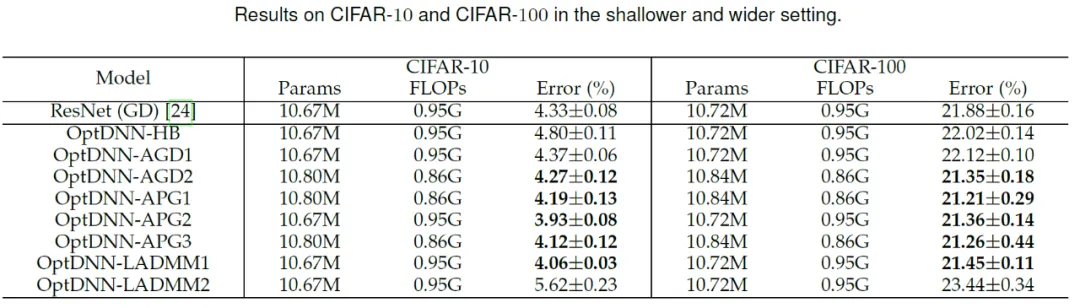
그런 다음 OptDNN은 넓고 얕은 CIF에서 수행됩니다. 및 각각 좁은 깊이 설정 AR 데이터 세트를 대상으로 이미지 분류 작업에 대한 실험을 수행하였고, 그 결과를 Table 3과 4에 나타내었다. 실험은 모두 강력한 데이터 확대 설정 하에서 수행되었습니다. 일부 OptDNN은 동일하거나 더 작은 FLOP 오버헤드에서 ResNet보다 더 작은 오류율을 달성한 것을 볼 수 있습니다. 논문에서도 ResNet과 DenseNet 설정으로 실험을 진행했고 비슷한 실험 결과를 얻었습니다. wide wide shally 설정에서 optdnn의 실험 결과 3 좁은 깊이 설정에서 optdnn의 실험 결과

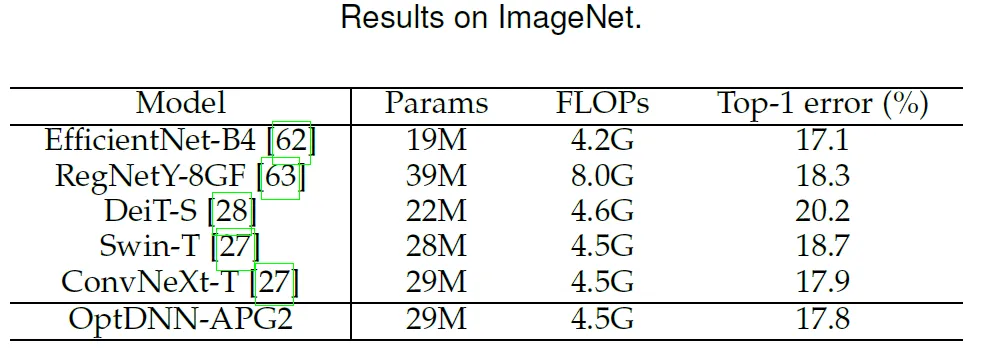
이 논문은 이전 성능을 더 선택합니다. 더 나은 Optdnn- APG2 네트워크는 ConvNext 및 ViT 설정 하에서 ImageNet 데이터 세트에서 추가 테스트되었습니다. OptDNN-APG2의 네트워크 구조는 그림 5에 나와 있으며 실험 결과는 표 5와 6에 나와 있습니다. OptDNN-APG2는 동일한 너비의 ConvNext 및 ViT를 초과하는 정확도를 달성하여 이 아키텍처 설계 방법의 신뢰성을 더욱 검증했습니다.

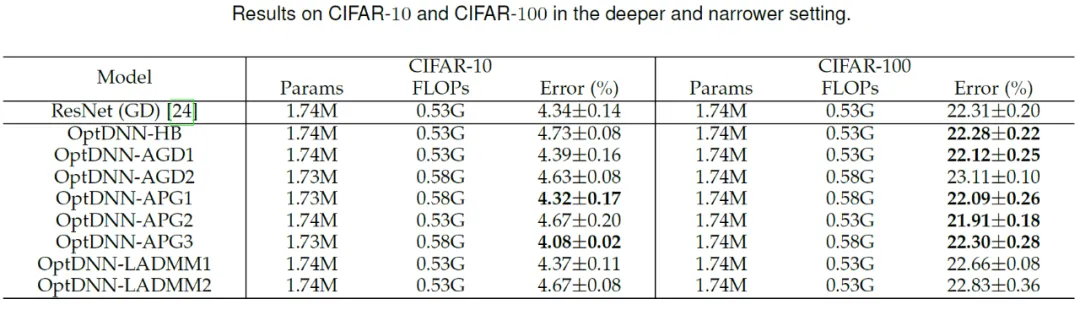그림 5 OptDNN-APG2의 네트워크 구조

표 5 ImageNet의 OptDNN-APG2 성능 비교

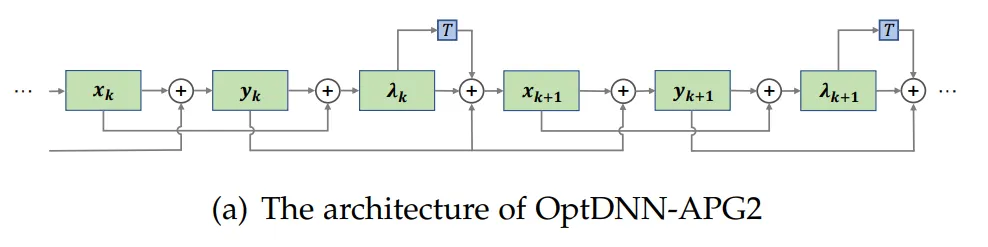
표 6 DNN-AP G2와 등방성) 성능 비교 of ConvNeXt 및 ViT

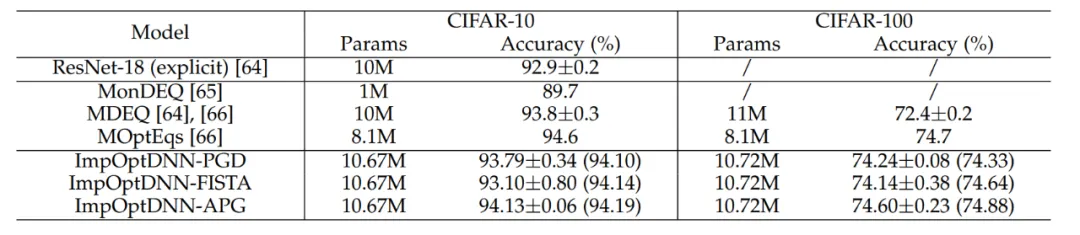
마지막으로 논문에서는 Proximal Gradient Descent 및 FISTA와 같은 알고리즘을 기반으로 3개의 암시적 네트워크를 설계하고 명시적 ResNet과 일반적으로 사용되는 일부 암시적 네트워크를 사용하여 CIFAR 데이터 세트에 대한 실험을 수행했습니다. 비교를 위해 실험 결과 표 7에 나와 있습니다. 세 가지 암시적 네트워크 모두 고급 암시적 네트워크에 필적하는 실험 결과를 얻었으며 이는 방법의 유연성도 보여줍니다.

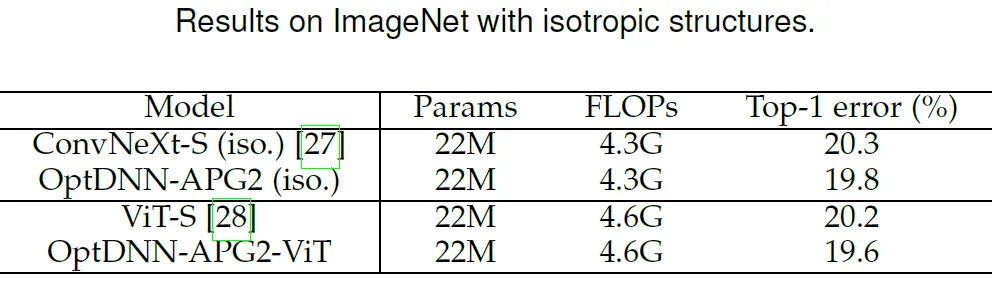표 7 암시적 네트워크의 성능 비교

요약

신경망 아키텍처 설계는 딥러닝의 핵심 이슈 중 하나입니다. 본 논문에서는 1차 최적화 알고리즘을 사용하여 보편적인 근사 속성을 갖는 신경망 아키텍처를 설계하기 위한 통합 프레임워크를 제안하고 최적화 설계 네트워크 아키텍처 패러다임을 기반으로 방법을 확장합니다. 이 방법은 네트워크 모듈에 중점을 둔 대부분의 기존 아키텍처 설계 방법과 결합할 수 있으며, 계산 노력을 거의 추가하지 않고도 효율적인 모델을 설계할 수 있습니다. 이론적으로 이 논문은 수렴 최적화 알고리즘에 의해 유도된 네트워크 아키텍처가 온화한 조건에서 보편적인 근사 속성을 가지며 NODE와 일반적인 교차 계층 연결 네트워크의 표현 기능을 연결한다는 것을 증명합니다. 또한 이 방식은 NAS, SNN 아키텍처 설계 등의 분야와 결합해 보다 효율적인 네트워크 아키텍처를 설계할 수 있을 것으로 기대된다.

위 내용은 1차 최적화 알고리즘에서 영감을 받아 Peking University Lin Zhouchen 팀은 보편적 근사 속성을 갖춘 신경망 아키텍처의 설계 방법을 제안했습니다.의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!