Schram의 정렬 - 공정성에 기반한 정렬 학습
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWB앞으로
- 2024-02-07 14:50:31783검색
국제학술대회 AIBT 2023에서 Ratidar Technologies LLC는 공정성 기반 순위 학습 알고리즘을 발표하고 학회 최우수 논문 보고서상을 수상했습니다. Skellam Rank라고 불리는 이 알고리즘은 통계 원리를 최대한 활용하고 pairwise Ranking과 행렬 분해 기술을 결합하여 추천 시스템의 정확성과 공정성 문제를 해결합니다. 추천 시스템에는 혁신적인 순위 학습 알고리즘이 거의 없기 때문에 Schramam의 순위 알고리즘은 컨퍼런스에서 연구상을 받을 정도로 좋은 성능을 보였습니다. 다음은 Schram 알고리즘의 기본 원리를 소개합니다.
먼저 푸아송 분포를 떠올려 보겠습니다.
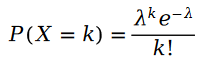
푸아송 분포 매개변수의 계산 공식은 다음과 같습니다.
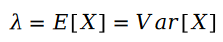
두 가지 포아송 변수의 차이점은 Schramm 분포입니다.
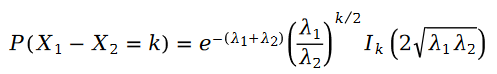
공식에는 다음이 포함됩니다.
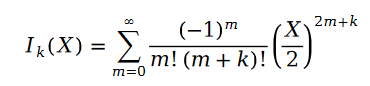
이 함수를 제1종 베셀 함수라고 합니다.
이러한 통계의 가장 기본적인 개념을 가지고 페어와이즈 랭킹 학습 추천 시스템을 구축해보자!
우리는 먼저 사용자의 아이템 평가가 포아송 분포 개념이라고 믿습니다. 즉, 사용자 아이템 평가 값은 다음과 같은 확률 분포를 따른다.
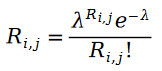
사용자 아이템 평가 과정을 포아송 과정으로 설명할 수 있는 이유는 사용자 아이템 평가에 매튜 효과가 있기 때문이다. 즉, 평점이 높은 사용자는 더 많은 평점을 가지므로 항목을 평가한 사람의 수를 사용하여 해당 항목에 대한 평점 분포를 대략적으로 계산할 수 있습니다. 항목을 평가하는 사람들의 수는 어떤 무작위 과정을 따르나요? 당연히 포아송 과정(Poisson process)을 생각해 보겠습니다. 사용자가 항목을 평가할 확률은 얼마나 많은 사람이 해당 항목을 평가할 확률과 유사하므로 자연스럽게 포아송 프로세스를 사용하여 사용자가 항목을 평가하는 프로세스를 대략적으로 계산할 수 있습니다.
포아송 과정의 매개변수를 표본 데이터의 통계량으로 대체하고 다음 공식을 얻습니다.
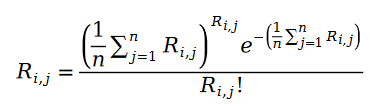
아래에서 Pariwise Ranking의 최대 우도 함수 공식을 정의합니다. 우리 모두 알고 있듯이 소위 쌍별 순위(Pairwise Ranking)는 모델 매개변수를 해결하기 위해 최대 우도 함수를 사용하여 모델이 데이터 샘플에서 알려진 순위 쌍의 관계를 최대한 유지할 수 있음을 의미합니다.
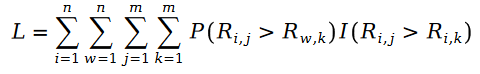
공식의 R은 포아송 분포이므로 차이점은 Schramam 분포입니다. 즉,
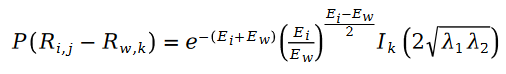
여기서 변수 E는 다음과 같이 정의됩니다.
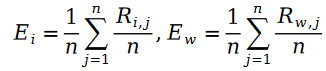
우리는 Schramam 분포를 호출합니다. 이 공식은 최대 우도 함수의 손실 함수 L에 가져오고 다음 공식을 얻습니다.
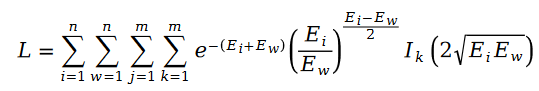
변수 E에 나타나는 사용자 평가 값 R에서 행렬 분해를 사용합니다. 그것을 해결하기 위해. 행렬 분해에서 매개변수 사용자 특징 벡터 U와 항목 특징 벡터 V를 해결 변수로 사용합니다.
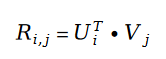
여기서 먼저 행렬 분해의 개념을 검토합니다. 행렬 분해의 개념은 2010년경에 제안된 추천 시스템 알고리즘이다. 이 알고리즘은 역사상 가장 성공적인 추천 시스템 알고리즘 중 하나라고 할 수 있다. 오늘날까지도 다수의 추천 시스템 회사에서는 행렬 분해 알고리즘을 온라인 시스템의 기본으로 사용하고 있으며 인기 있는 클래식 추천 알고리즘인 DeepFM의 중요한 구성 요소인 Factorization Machine도 행렬 분해 알고리즘의 후속 개선입니다. 추천 시스템 알고리즘 버전은 행렬 분해와 불가분의 관계가 있습니다. 행렬 분해 알고리즘에 대한 랜드마크 논문이 2007년에 발표되었는데, 바로 확률적 행렬 분해(Probabilistic Matrix Factorization)입니다. 저자는 통계적 학습 모델을 사용하여 선형 대수학에서 행렬 분해의 개념을 재구성하여 처음으로 행렬 분해에 탄탄한 수학적 이론적 기반을 제공했습니다.
행렬 분해의 기본 개념은 벡터의 내적을 사용하여 사용자 평가 행렬의 차원을 줄이면서 알 수 없는 사용자 평가를 효율적으로 예측하는 것입니다. 행렬 분해의 손실 함수는 다음과 같습니다.
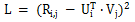
행렬 분해 알고리즘에는 다양한 변형이 있습니다. 예를 들어 Shanghai Jiao Tong University에서 제안한 SVDFeature는 벡터 U와 V를 선형 조합 형태로 모델링합니다. , 행렬 분해 문제는 특성 공학의 문제가 됩니다. SVDFeature는 행렬 분해 분야의 획기적인 논문이기도 합니다. 모델링 목적을 달성하기 위해 알 수 없는 사용자 등급을 대체하기 위해 행렬 분해를 쌍별 순위(Pairwise Ranking)에 적용할 수 있습니다. 클래식 응용 사례에는 베이지안 쌍별 순위(Bayesian pairwise Ranking)의 BPR-MF 알고리즘이 포함되며 Schramam 순위 알고리즘은 동일한 아이디어를 따릅니다.
우리는 확률적 경사하강법을 사용하여 Schramam 정렬 알고리즘을 해결합니다. 확률적 경사하강법은 해법의 목적을 달성하기 위해 해결 과정에서 손실 함수를 크게 단순화할 수 있으므로 손실 함수는 다음 공식이 됩니다.
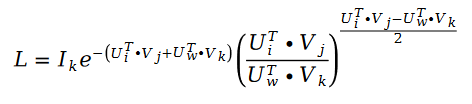
확률적 경사하강법을 사용하여 미지 매개변수 U와 V에 대한 해결을 계산합니다. , 다음과 같이 반복 공식을 얻습니다.
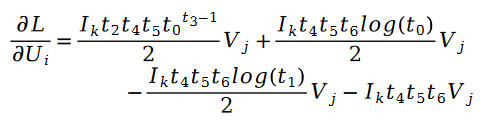
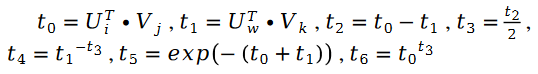
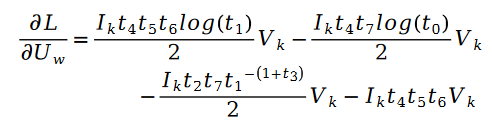
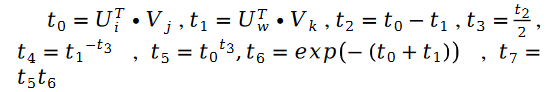
그 중: 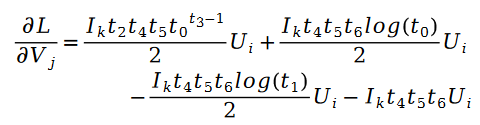
추가: 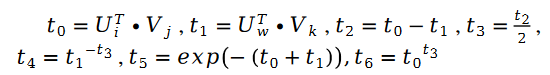
그 중: 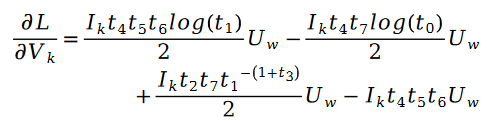
전체 알고리즘 프로세스를 설명하기 위해 다음 의사 코드를 사용합니다. 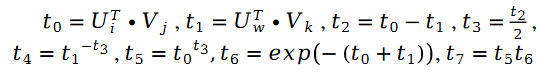
알고리즘의 유효성을 검증하기 위해 논문 작성자는 MovieLens 1 Million Dataset 및 LDOS-CoMoDa Dataset에서 테스트했습니다. 첫 번째 데이터 세트에는 6040명의 사용자와 3706개의 영화에 대한 평점이 포함되어 있습니다. 전체 평점 데이터 세트에는 약 100만 개의 평점 데이터가 포함되어 있으며 추천 시스템 분야에서 가장 잘 알려진 평점 데이터 모음 중 하나입니다. 두 번째 데이터 수집은 슬로베니아에서 나온 것으로 인터넷에서는 보기 드문 시나리오 기반 추천 시스템 데이터 수집이다. 데이터 세트에는 121명의 사용자와 1232개의 영화에 대한 평가가 포함되어 있습니다. 저자는 Schram의 정렬을 다른 9가지 추천 시스템 알고리즘과 비교했습니다. 주요 평가 지표는 MAE(Mean Absolute Error, 정확성 테스트에 사용됨) 및 Degree of Matthew Effect(주로 공정성 테스트에 사용됨)입니다.
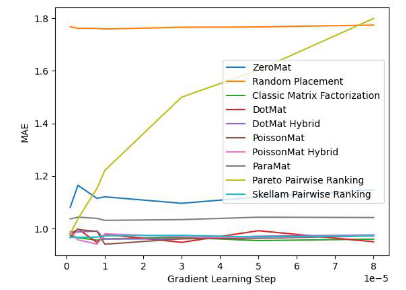
그림 1 . MovieLens 1 Million Dataset(MAE 표시기)
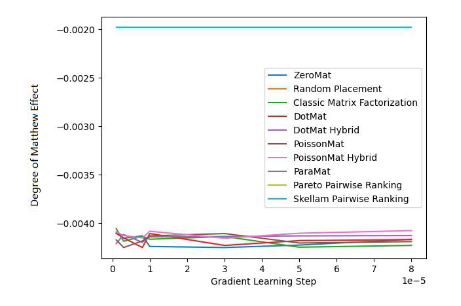
그림 2. MovieLens 1 Million Dataset(Matthew 효과 표시기)
그림 1과 그림 2를 통해 Schram의 정렬이 MAE에서 잘 수행되었음을 확인했습니다. 지표이지만 그리드 검색의 전체 실험 동안 다른 알고리즘보다 항상 더 나은 성능을 보장하지는 않았습니다. 그러나 그림 2에서는 Schramam의 정렬이 공정성 지수에서 다른 9개 추천 시스템 알고리즘보다 훨씬 앞서 있음을 알 수 있습니다.
LDOS-CoMoDa 데이터 세트에서 이 알고리즘의 성능을 살펴보겠습니다.
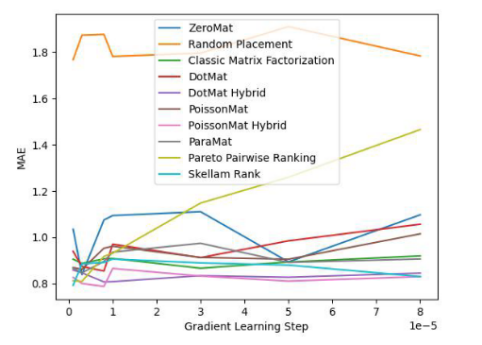
그림 3. LDOS-CoMoDa 데이터 세트(MAE 표시기)
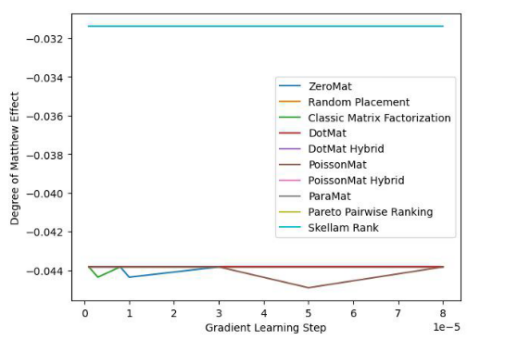
그림 4. LDOS- CoMoDa Dataset (Matthew 효과 지표의 정도)
그림 3과 그림 4를 통해 Schram의 정렬이 공정성 지표에서 1위를 차지하고 정확도 지표에서 좋은 성능을 발휘한다는 것을 알 수 있습니다. 결론은 이전 실험과 유사하다.
Schramm 정렬은 포아송 분포, 행렬 분해, 쌍별 순위 등의 개념을 결합한 것으로 추천 시스템에서는 보기 드문 순위 학습 알고리즘입니다. 기술 분야에서는 랭킹러닝 기술을 마스터한 사람이 딥러닝을 마스터한 사람의 1/6에 불과해 랭킹러닝이 희소한 기술이다. 그리고 추천 시스템 분야에서 독창적인 순위 학습을 창안할 수 있는 인재는 더욱 적습니다. 순위 학습 알고리즘은 점수 예측이라는 협소한 관점에서 벗어나 가장 중요한 것은 점수가 아닌 순서라는 사실을 깨닫게 해줍니다. 공정성을 기반으로 한 순위 학습은 현재 정보 검색 분야에서 매우 인기가 있으며, 특히 SIGIR과 같은 상위 컨퍼런스에서는 공정성을 기반으로 한 추천 시스템에 대한 논문이 매우 환영 받고 있으며 독자들의 관심을 끌기를 바랍니다.
저자소개
왕하오 전 펀플러스 인공지능연구소장. 그는 ThoughtWorks, Douban, Baidu 및 Sina와 같은 회사에서 기술 및 기술 임원직을 역임했습니다. 그는 인터넷 기업, 금융 기술, 게임 및 기타 기업에서 12년 동안 근무하면서 인공 지능, 컴퓨터 그래픽, 블록체인 등 분야에 대한 깊은 통찰력과 풍부한 경험을 가지고 있습니다. 국제학술대회 및 저널에 42편의 논문을 게재하였으며, IEEE SMI 2008 Best Paper Award, ICBDT 2020 / IEEE ICISCAE 2021 / AIBT 2023 Best Paper Report Award를 수상하였습니다.
위 내용은 Schram의 정렬 - 공정성에 기반한 정렬 학습의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!

