Bellman Ford 알고리즘 및 Python 구현에 대한 자세한 설명

Bellman Ford 알고리즘은 가중치 그래프에서 대상 노드에서 다른 노드까지의 최단 경로를 찾을 수 있습니다. 이는 Dijkstra 알고리즘과 매우 유사하며 Bellman-Ford 알고리즘은 음수 가중치를 갖는 그래프를 처리할 수 있으며 구현 측면에서 비교적 간단합니다.

Bellman Ford 알고리즘의 원리에 대한 자세한 설명

Bellman Ford 알고리즘은 시작 정점부터 다른 모든 정점까지의 경로 길이를 과대평가하여 과대평가된 경로보다 짧은 새로운 경로를 반복적으로 찾습니다.

각 노드의 경로 거리를 기록하고 싶기 때문에 이를 n 크기의 배열에 저장할 수 있습니다. n은 또한 노드 수를 나타냅니다.

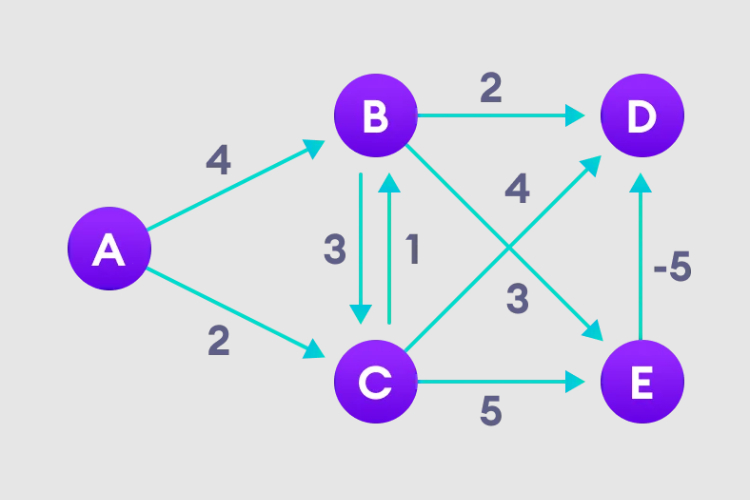
인스턴스 다이어그램

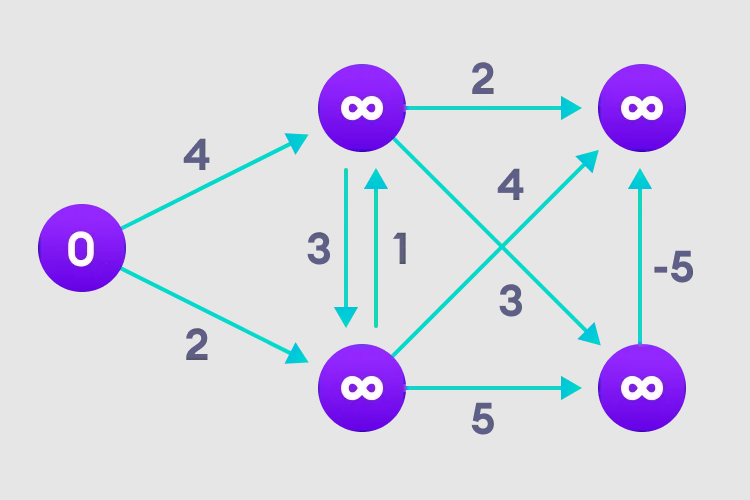
1. 시작 노드를 선택하고 다른 모든 정점에 무한히 할당하고 경로 값을 기록합니다.

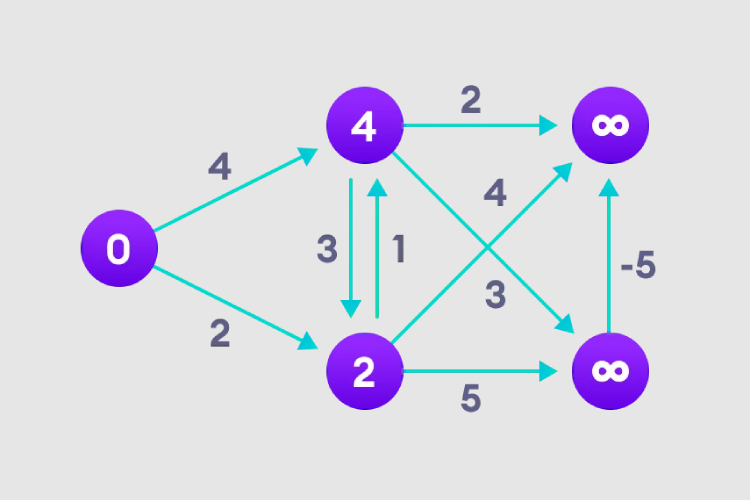
2. 각 Edge를 방문하여 완화 작업을 수행하여 최단 경로를 지속적으로 업데이트합니다.

3. 최악의 경우 가장 짧은 노드 경로 길이를 N-1번 재조정해야 할 수 있으므로 이 작업을 N-1번 수행해야 합니다.

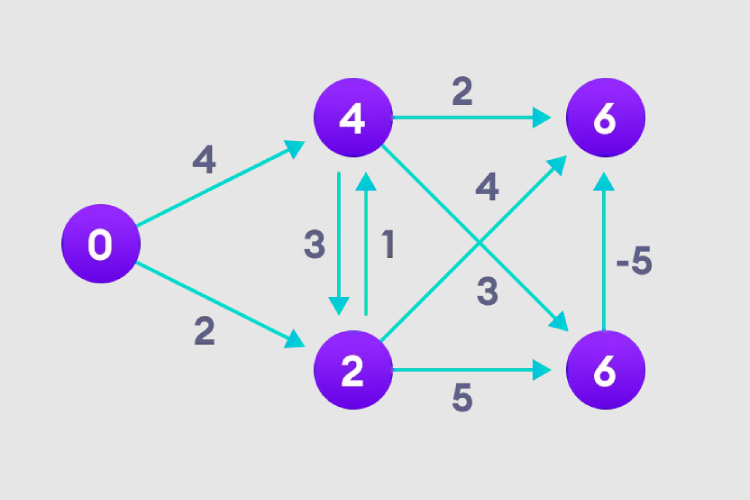
4. 오른쪽 상단 모서리에 있는 노드가 경로 길이를 어떻게 조정하는지 확인하세요.

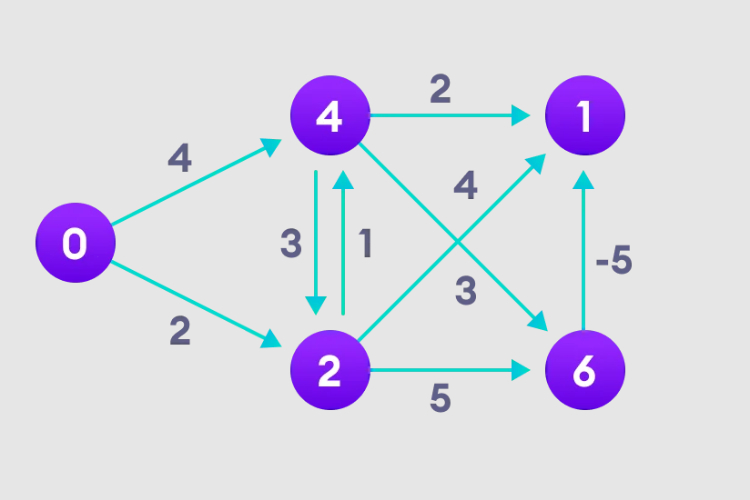
5. 모든 노드의 경로 길이를 확인한 후 음수 루프가 있는지 확인합니다.

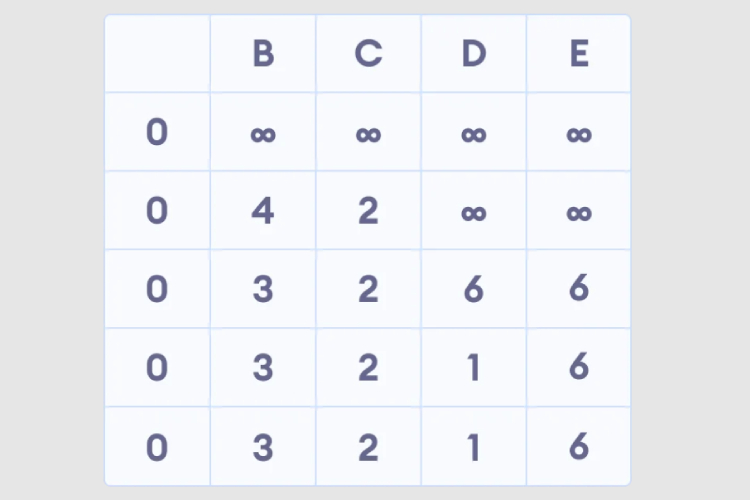
Python은 Bellman Ford 알고리즘을 구현합니다

class Graph:

    def __init__(self, vertices):
        self.V = vertices   # Total number of vertices in the graph
        self.graph = []     # Array of edges

    def add_edge(self, s, d, w):
        self.graph.append([s, d, w])

    def print_solution(self, dist):
        print("Vertex Distance from Source")
        for i in range(self.V):
            print("{0}\t\t{1}".format(i, dist[i]))

    def bellman_ford(self, src):

        dist = [float("Inf")] * self.V
        dist[src] = 0

        for _ in range(self.V - 1):
            for s, d, w in self.graph:
                if dist[s] != float("Inf") and dist[s] + w < dist[d]:
                    dist[d] = dist[s] + w

        for s, d, w in self.graph:
            if dist[s] != float("Inf") and dist[s] + w < dist[d]:
                print("Graph contains negative weight cycle")
                return

        self.print_solution(dist)

g = Graph(5)
g.add_edge(0, 1, 5)
g.add_edge(0, 2, 4)
g.add_edge(1, 3, 3)
g.add_edge(2, 1, 6)
g.add_edge(3, 2, 2)

g.bellman_ford(0)

위 내용은 Bellman Ford 알고리즘 및 Python 구현에 대한 자세한 설명의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!