Python을 사용하여 미니 배치 경사하강법 알고리즘을 구현하기 위한 코드 논리
- PHPz앞으로
- 2024-01-22 12:33:191627검색
theta = 모델 매개변수, max_iters = 에포크 수라고 가정합니다. itr=1,2,3,...,max_iters의 경우: mini_batch(X_mini,y_mini)의 경우:
배치 X_mini의 전달:
1. 미니 배치 예측
2. 매개변수 예측 오류 계산(J(theta))
전송 후: 기울기 계산(theta)=J(theta)wrt theta의 부분 도함수
업데이트 매개변수: theta=theta–learning_rate*gradient(theta )
Python은 경사하강법 알고리즘 코드 흐름을 구현합니다.
1단계: 종속성을 가져오고, 선형 회귀를 위한 데이터를 생성하고, 생성된 데이터를 시각화합니다. 8000개의 데이터 예를 들면 각 예에는 2개의 속성 특성이 있습니다. 이러한 데이터 샘플은 각각 7200개와 800개 샘플로 훈련 세트(X_train, y_train)와 테스트 세트(X_test, y_test)로 더 나뉩니다.
import numpy as np import matplotlib.pyplot as plt mean=np.array([5.0,6.0]) cov=np.array([[1.0,0.95],[0.95,1.2]]) data=np.random.multivariate_normal(mean,cov,8000) plt.scatter(data[:500,0],data[:500,1],marker='.') plt.show() data=np.hstack((np.ones((data.shape[0],1)),data)) split_factor=0.90 split=int(split_factor*data.shape[0]) X_train=data[:split,:-1] y_train=data[:split,-1].reshape((-1,1)) X_test=data[split:,:-1] y_test=data[split:,-1].reshape((-1,1)) print(& quot Number of examples in training set= % d & quot % (X_train.shape[0])) print(& quot Number of examples in testing set= % d & quot % (X_test.shape[0]))
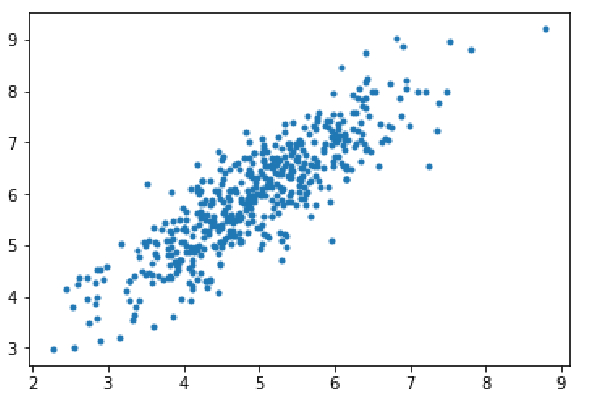
훈련 세트의 예 수 = 7200 테스트 세트의 예 수 = 800
2단계:
미니 배치 경사하강법을 사용하여 선형 회귀를 구현하는 코드입니다. GradientDescent()는 주요 구동 기능이고 다른 기능은 보조 기능입니다.
예측하기 - Hypothese()
기울기 계산 - Gradient()
오류 계산 - Cost()
미니 배치 만들기 - create_mini_batches( )
드라이버 함수는 매개변수를 초기화하고, 모델에 대한 최적의 매개변수 세트를 계산하고, 매개변수가 업데이트될 때 오류 기록이 포함된 목록과 함께 해당 매개변수를 반환합니다.
def hypothesis(X,theta):
return np.dot(X,theta)
def gradient(X,y,theta):
h=hypothesis(X,theta)
grad=np.dot(X.transpose(),(h-y))
return grad
def cost(X,y,theta):
h=hypothesis(X,theta)
J=np.dot((h-y).transpose(),(h-y))
J/=2
return J[0]
def create_mini_batches(X,y,batch_size):
mini_batches=[]
data=np.hstack((X,y))
np.random.shuffle(data)
n_minibatches=data.shape[0]//batch_size
i=0
for i in range(n_minibatches+1):
mini_batch=data[i*batch_size:(i+1)*batch_size,:]
X_mini=mini_batch[:,:-1]
Y_mini=mini_batch[:,-1].reshape((-1,1))
mini_batches.append((X_mini,Y_mini))
if data.shape[0]%batch_size!=0:
mini_batch=data[i*batch_size:data.shape[0]]
X_mini=mini_batch[:,:-1]
Y_mini=mini_batch[:,-1].reshape((-1,1))
mini_batches.append((X_mini,Y_mini))
return mini_batches
def gradientDescent(X,y,learning_rate=0.001,batch_size=32):
theta=np.zeros((X.shape[1],1))
error_list=[]
max_iters=3
for itr in range(max_iters):
mini_batches=create_mini_batches(X,y,batch_size)
for mini_batch in mini_batches:
X_mini,y_mini=mini_batch
theta=theta-learning_rate*gradient(X_mini,y_mini,theta)
error_list.append(cost(X_mini,y_mini,theta))
return theta,error_listgradientDescent() 함수를 호출하여 모델 매개변수(세타)를 계산하고 오류 함수의 변화를 시각화합니다.
theta,error_list=gradientDescent(X_train,y_train)
print("Bias=",theta[0])
print("Coefficients=",theta[1:])
plt.plot(error_list)
plt.xlabel("Number of iterations")
plt.ylabel("Cost")
plt.show()Deviation=[0.81830471]Coefficient=[[1.04586595]]
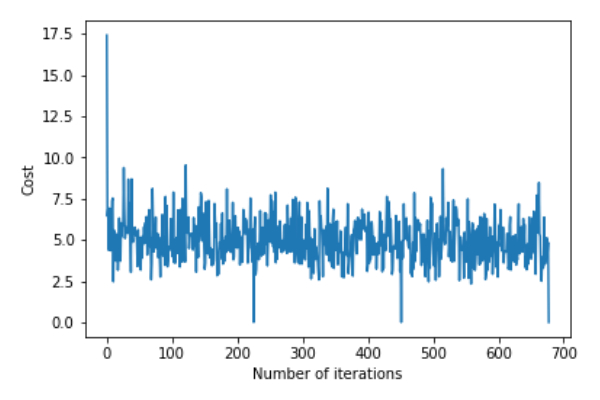
3단계: 테스트 세트를 예측하고 예측의 평균 절대 오차를 계산합니다.
y_pred=hypothesis(X_test,theta) plt.scatter(X_test[:,1],y_test[:,],marker='.') plt.plot(X_test[:,1],y_pred,color='orange') plt.show() error=np.sum(np.abs(y_test-y_pred)/y_test.shape[0]) print(& quot Mean absolute error=",error)
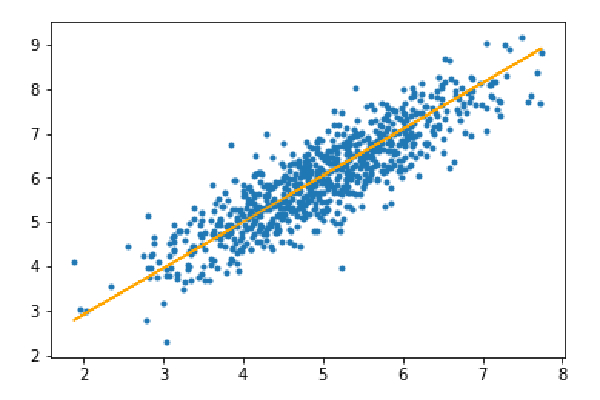
평균 절대 오차=0.4366644295854125
주황색 선은 최종 가설 함수를 나타냅니다: theta[0]+theta[1]*X_test[:,1]+theta[2]*X_test[:,2]=0
위 내용은 Python을 사용하여 미니 배치 경사하강법 알고리즘을 구현하기 위한 코드 논리의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!

