이진수 시스템 - C/C++의 산술 덧셈 오버플로?

2의 보수 체계는 컴퓨터 아키텍처에서 널리 사용됩니다.

N비트 2의 보수 체계는 -2n-1부터 2n-1-1까지의 숫자를 나타낼 수 있습니다.

4자리는 (-8부터 7)까지의 숫자를 나타낼 수 있습니다.

5자리는 (-16부터 7까지의 숫자를 나타낼 수 있습니다. 15) 숫자는 2의 보수 체계를 따릅니다.

2개의 N 비트 2의 보수 숫자가 추가되고 답이 너무 커서 해당 N 비트 그룹에 맞지 않는 경우에도 오버플로가 발생합니다.

컴퓨터에는 N비트 고정 레지스터가 포함되어 있습니다. 두 개의 N자리 숫자를 더한 결과는 가장 큰 N+1자리 숫자가 됩니다.

캐리 플래그는 추가 비트를 저장합니다. 그러나 캐리가 항상 오버플로를 나타내는 것은 아닙니다.

오버플로 감지

-

• 두 개의 음수를 더한 결과가 양수이거나

• 두 개의 음수를 더한 결과가 음수인 경우.

따라서 두 피연산자의 MSB(최상위 비트)와 결과를 확인하여 오버플로를 감지할 수 있습니다. 그러나 3비트 비교기를 구현하는 대신 MSB의 캐리 및 캐리 출력을 확인하여 오버플로를 감지할 수 있습니다. 2의 보수의 N비트 덧셈을 고려합니다.

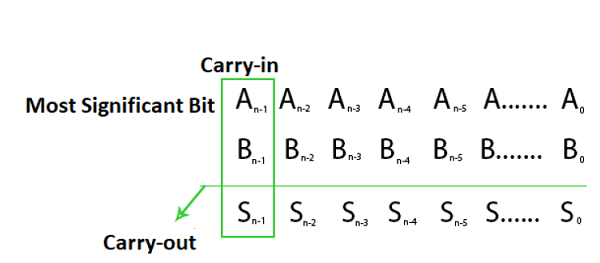
캐리 입력과 캐리 출력이 같지 않을 때 오버플로가 발생합니다. 위의 오버플로 표현식은 다음 분석을 통해 논의할 수 있습니다.

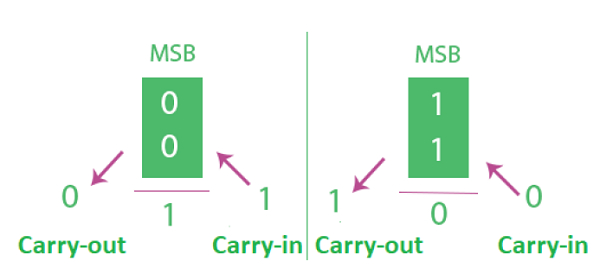
첫 번째 그림에서 두 숫자의 최상위 비트는 0으로 이는 양수임을 나타냅니다. 여기서 캐리 입력이 1이면 결과의 최상위 비트가 1이 되어 결과가 음수(오버플로)이고 캐리 출력이 0임을 나타냅니다. 반입과 반출이 같지 않아 오버플로가 발생합니다.

두 번째 그림에서 두 숫자의 최상위 비트는 1로, 이는 음수임을 나타냅니다. 여기서 캐리 입력이 0이면 결과의 최상위 비트가 0이 되어 결과가 양수(오버플로)임을 나타내며 캐리 출력은 1이 됩니다. 반입과 반출이 같지 않아 오버플로가 발생합니다.

따라서 MSB의 반입 및 반출은 넘침을 감지하기에 충분합니다.

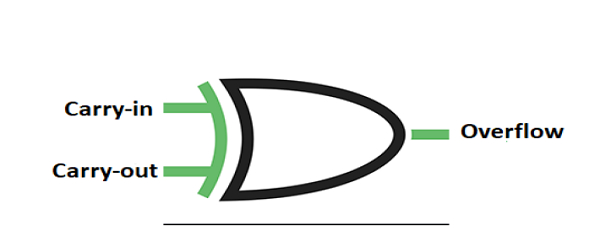
위의 XOR 게이트를 사용하여 오버플로를 감지할 수 있습니다.

위 내용은 이진수 시스템 - C/C++의 산술 덧셈 오버플로?의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!