Python을 이용한 거래 전략 및 포트폴리오 분석

이 글에서는 거래 전략의 성과를 측정해 보겠습니다. 그리고 채권, 주식, 부동산 등 4가지 자산 클래스를 사용하는 간단한 모멘텀 거래 전략을 개발할 것입니다. 이러한 자산 클래스는 상관관계가 낮아서 탁월한 위험 균형 옵션이 됩니다.

모멘텀 트레이딩 전략

이 전략은 모멘텀을 기반으로 합니다. 왜냐하면 트레이더와 투자자는 광범위한 시장과 기간에 걸쳐 볼 수 있는 모멘텀의 영향을 오랫동안 알고 있었기 때문입니다. 그래서 우리는 이를 모멘텀 전략이라고 부릅니다. 추세 추종 또는 시계열 모멘텀(TSM)은 단일 도구에서 이러한 전략을 사용하는 또 다른 이름입니다. 우리는 기본 모멘텀 전략을 수립하고 TCS에서 테스트하여 그것이 어떻게 수행되는지 확인할 것입니다.

TSM 전략 분석

먼저 일부 라이브러리를 가져옵니다

import numpy as np
 import pandas as pd
 import matplotlib.pyplot as plt
 import yfinance as yf
 import ffn
 %matplotlib inline

기본 모멘텀 전략 기능인 TSMStrategy를 구축합니다. 이 함수는 시계열의 로그 반환, 관심 기간 및 단락 허용 여부에 대한 부울 변수를 통해 예상 성능을 반환합니다.

def TSMStrategy(returns, period=1, shorts=False):
if shorts:
position = returns.rolling(period).mean().map(
lambda x: -1 if x <= 0 else 1)
else:
position = returns.rolling(period).mean().map(
lambda x: 0 if x <= 0 else 1)
performance = position.shift(1) * returns
return performance
 ticker = 'TCS'
 yftcs = yf.Ticker(ticker)
 data = yftcs.history(start='2005-01-01', end='2021-12-31')
 returns = np.log(data['Close'] / data['Close'].shift(1)).dropna()
 performance = TSMStrategy(returns, period=1, shorts=False).dropna()
 years = (performance.index.max() - performance.index.min()).days / 365
 perf_cum = np.exp(performance.cumsum())
 tot = perf_cum[-1] - 1
 ann = perf_cum[-1] ** (1 / years) - 1
 vol = performance.std() * np.sqrt(252)
 rfr = 0.02
 sharpe = (ann - rfr) / vol
 print(f"1-day TSM Strategy yields:" +
f"nt{tot*100:.2f}% total returns" +
f"nt{ann*100:.2f}% annual returns" +
f"nt{sharpe:.2f} Sharpe Ratio")
 tcs_ret = np.exp(returns.cumsum())
 b_tot = tcs_ret[-1] - 1
 b_ann = tcs_ret[-1] ** (1 / years) - 1
 b_vol = returns.std() * np.sqrt(252)
 b_sharpe = (b_ann - rfr) / b_vol
 print(f"Baseline Buy-and-Hold Strategy yields:" +
f"nt{b_tot*100:.2f}% total returns" +
f"nt{b_ann*100:.2f}% annual returns" +
f"nt{b_sharpe:.2f} Sharpe Ratio")

함수 출력은 다음과 같습니다.

1-day TSM Strategy yields:
 -45.15% total returns
 -7.10% annual returns
 -0.17 Sharpe Ratio
 Baseline Buy-and-Hold Strategy yields:
 -70.15% total returns
 -13.78% annual returns
 -0.22 Sharpe Ratio

합리적인 연간 수익률 측면에서 1일 TSM 전략이 매수 후 보유 전략보다 성능이 뛰어납니다. 1일 룩백에는 잘못된 추세가 많이 포함될 수 있으므로 서로 다른 기간을 시도하여 비교 방법을 확인했습니다. 여기서 모델은 3일, 5일, 15일, 30일, 90일 동안 반복적으로 실행됩니다.

 import matplotlib.gridspec as gridspec
 periods = [3, 5, 15, 30, 90]
 fig = plt.figure(figsize=(12, 10))
 gs = fig.add_gridspec(4, 4)
 ax0 = fig.add_subplot(gs[:2, :4])
 ax1 = fig.add_subplot(gs[2:, :2])
 ax2 = fig.add_subplot(gs[2:, 2:])
 ax0.plot((np.exp(returns.cumsum()) - 1) * 100, label=ticker, linestyle='-')
 perf_dict = {'tot_ret': {'buy_and_hold': (np.exp(returns.sum()) - 1)}}
 perf_dict['ann_ret'] = {'buy_and_hold': b_ann}
 perf_dict['sharpe'] = {'buy_and_hold': b_sharpe}
 for p in periods:
log_perf = TSMStrategy(returns, period=p, shorts=False)
perf = np.exp(log_perf.cumsum())
perf_dict['tot_ret'][p] = (perf[-1] - 1)
ann = (perf[-1] ** (1/years) - 1)
perf_dict['ann_ret'][p] = ann
vol = log_perf.std() * np.sqrt(252)
perf_dict['sharpe'][p] = (ann - rfr) / vol
ax0.plot((perf - 1) * 100, label=f'{p}-Day Mean')
 
 ax0.set_ylabel('Returns (%)')
 ax0.set_xlabel('Date')
 ax0.set_title('Cumulative Returns')
 ax0.grid()
 ax0.legend()
 _ = [ax1.bar(i, v * 100) for i, v in enumerate(perf_dict['ann_ret'].values())]
 ax1.set_xticks([i for i, k in enumerate(perf_dict['ann_ret'])])
 ax1.set_xticklabels([f'{k}-Day Mean'
if type(k) is int else ticker for
k in perf_dict['ann_ret'].keys()],
rotation=45)
 ax1.grid()
 ax1.set_ylabel('Returns (%)')
 ax1.set_xlabel('Strategy')
 ax1.set_title('Annual Returns')
 _ = [ax2.bar(i, v) for i, v in enumerate(perf_dict['sharpe'].values())]
 ax2.set_xticks([i for i, k in enumerate(perf_dict['sharpe'])])
 ax2.set_xticklabels([f'{k}-Day Mean'
if type(k) is int else ticker for
k in perf_dict['sharpe'].keys()],
rotation=45)
 ax2.grid()
 ax2.set_ylabel('Sharpe Ratio')
 ax2.set_xlabel('Strategy')
 ax2.set_title('Sharpe Ratio')
 plt.tight_layout()
 plt.show()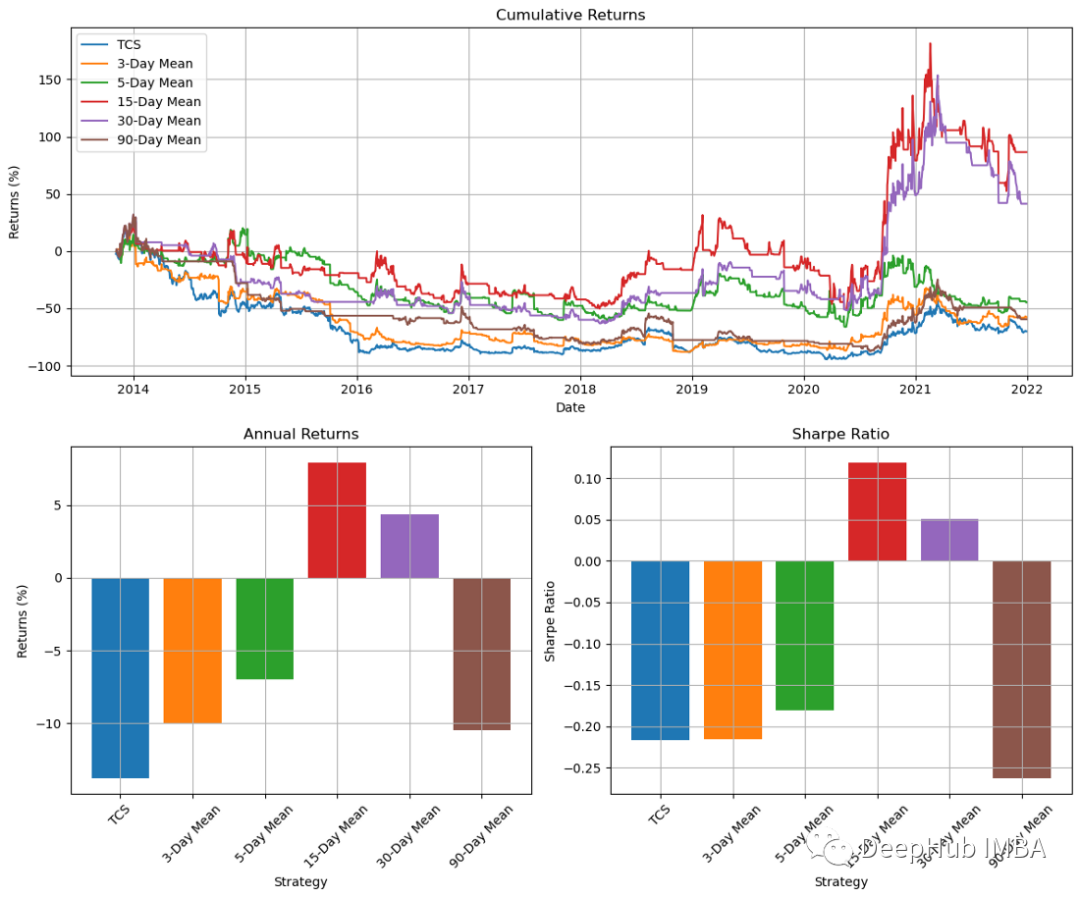

차트 결과를 보면 15일 모멘텀 지표가 가장 좋은 결과를 제공하는 것을 알 수 있습니다. 그러나 다른 기간에 대한 결과는 엇갈립니다. 이는 우리의 전략이 신뢰할 수 없다는 것을 보여줍니다. 따라서 15일 차트가 하향세이거나 평탄할 때 거래를 종료하는 대신 상단 근처에서 정지 또는 추적 정지를 사용하여 거래를 종료할 수도 있습니다.

포트폴리오 분석

지금까지 우리는 Python으로 거래 전략을 만들었습니다. 아래에서는 관찰과 분석을 용이하게 하기 위해 일반적인 포트폴리오 특성을 측정하고 표시할 것입니다.

포트폴리오 분석

먼저 중요한 라이브러리 몇 개를 가져와서 데이터 실행을 관찰하겠습니다.

import pandas_datareader.data as web
 stocks = ['SPY','GLD','TLT','HYG']
 
 data = web.DataReader(stocks,data_source='yahoo',start='01/01/2019')['Adj Close']
 data.sort_index(ascending=True,inplace=True)
 perf = data.calc_stats()
 perf.plot()

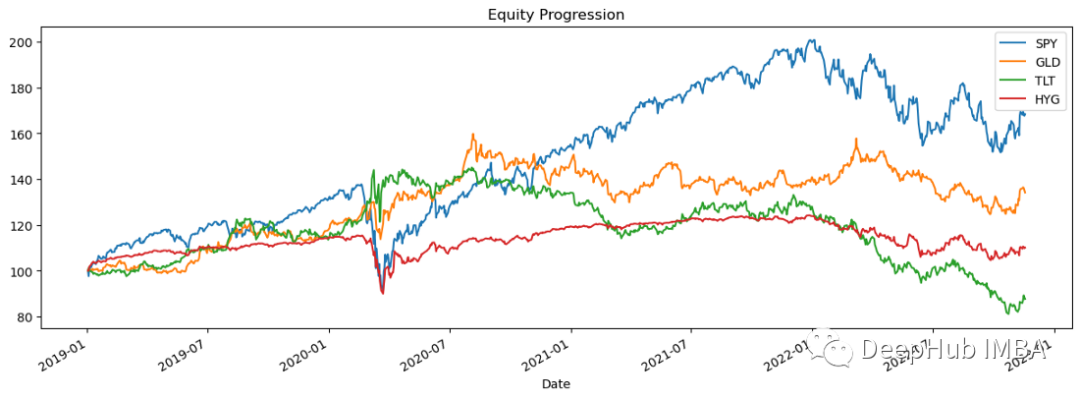
로그 반환

로그 반환은 지수 증가율을 계산하는 데 사용됩니다. 각 하위 기간의 가격 변동률을 계산하는 대신 해당 기간의 유기적 성장 지수를 계산합니다. 먼저 데이터의 각 주가에 대한 로그 수익률을 포함하는 df를 만든 다음 각 로그 수익률에 대한 히스토그램을 만듭니다.

 returns = data.to_log_returns().dropna()
 print(returns.head())
 
 
 Symbols SPY GLD TLT HYG
 Date
 2019-01-03 -0.024152 0.009025 0.011315 0.000494
 2019-01-04 0.032947 -0.008119 -0.011642 0.016644
 2019-01-07 0.007854 0.003453 -0.002953 0.009663
 2019-01-08 0.009351 -0.002712 -0.002631 0.006470
 2019-01-09 0.004663 0.006398 -0.001566 0.001193

히스토그램은 다음과 같습니다.

ax = returns.hist(figsize=(20, 10),bins=30)

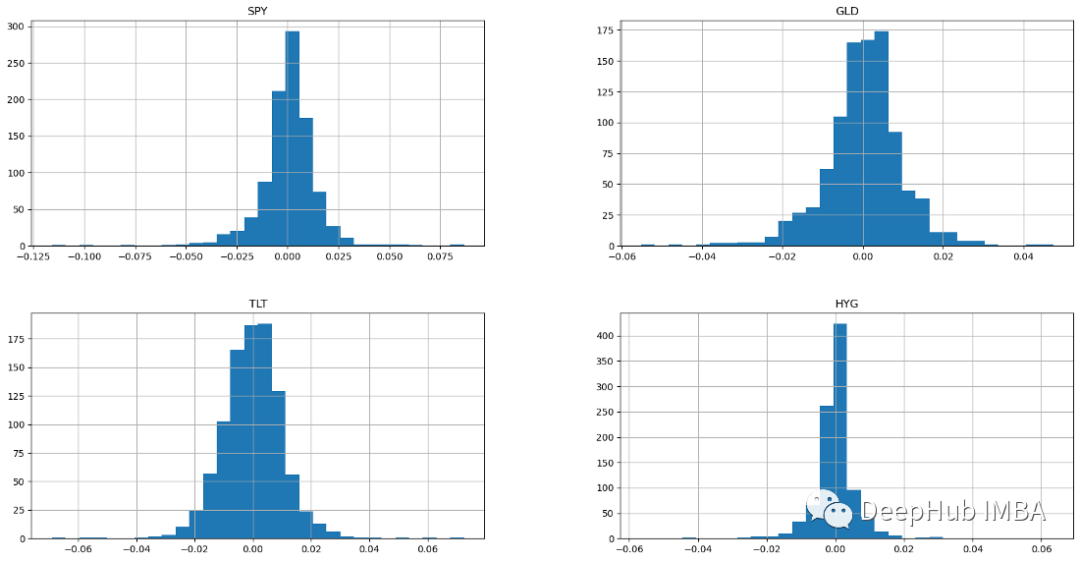
4가지 자산 클래스 모두 정규 분포의 히스토그램을 보여줍니다. 정규 분포를 갖는 표본은 산술 평균과 평균 위와 아래에 동일한 분포를 갖습니다(가우시안 분포라고도 알려진 정규 분포는 대칭입니다). 수익률이 정규 분포를 따르는 경우 수익률의 99% 이상이 평균의 3표준편차 내에 속할 것으로 예상됩니다. 이러한 종 모양의 정규 분포 특성을 통해 분석가와 투자자는 주식의 예상 수익률과 위험에 대해 더 나은 통계적 추론을 할 수 있습니다. 종형 곡선이 있는 주식은 일반적으로 변동성이 낮고 예측 가능한 블루칩입니다.

최대 되돌림 비율 DRAWDOWN

DRAWDOWN은 값이 상대적으로 낮은 수준으로 떨어지는 것을 의미합니다. 이는 투자자가 고려해야 할 중요한 위험 요소입니다. 감소하는 전략을 시각적으로 표현해 보겠습니다.

ffn.to_drawdown_series(data).plot(figsize=(15,10))

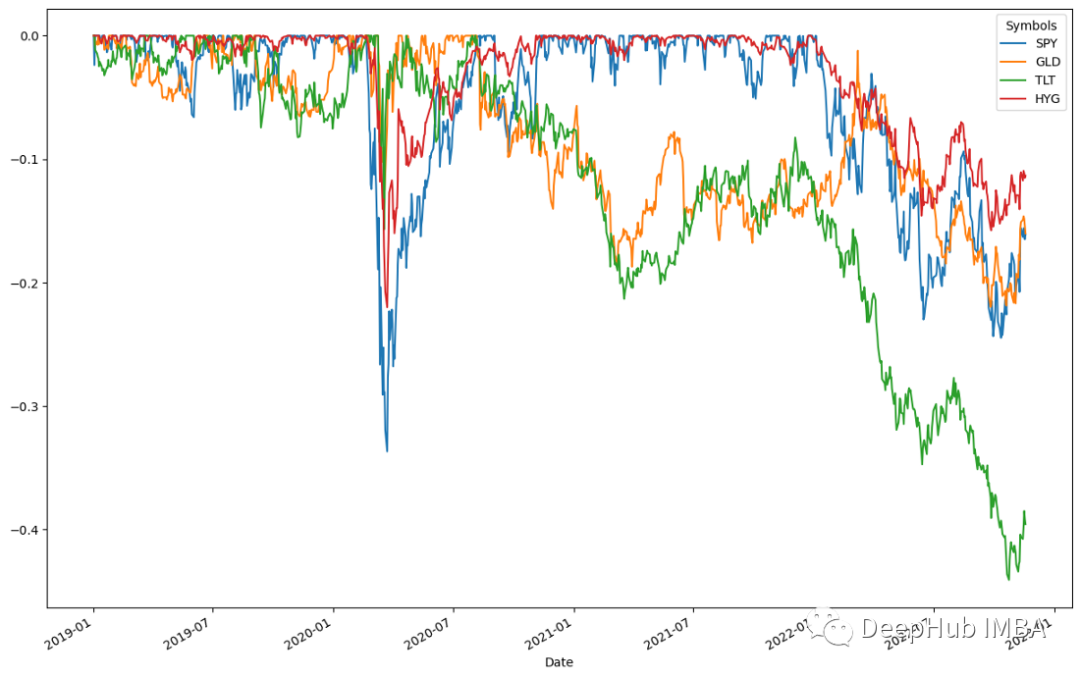
2020년 상반기 4개 자산 모두 하락했는데, SPY가 0.5%로 가장 큰 하락폭을 기록했습니다. 그러다가 2020년 상반기에는 모든 자산이 즉시 회복됐다. 이는 자산 회수율이 높다는 것을 의미합니다. 이들 자산은 2020년 7월경에 정점에 달했습니다. 이러한 추세에 따라 모든 자산 클래스는 회복이 정점에 도달한 후 완만하게 하락했습니다. 결과에 따르면 TLT는 2022년 하반기에 0.5%로 가장 큰 하락세를 겪다가 2023년 초 회복될 것으로 예상된다.

MARKOWITZ 평균 분산 최적화

1952년에 Markowitz는 현대 포트폴리오 이론이라고도 알려진 평균 분산 포트폴리오 이론을 제안했습니다. 투자자는 이러한 개념을 사용하여 주어진 위험 수준에 따라 기대 수익을 극대화하는 포트폴리오를 구성할 수 있습니다. Markowitz 방법을 기반으로 "최적 포트폴리오"를 생성할 수 있습니다.

returns.calc_mean_var_weights().as_format('.2%')
 #结果
 SPY 46.60%
 GLD 53.40%
 TLT 0.00%
 HYG 0.00%
 dtype: object

상관통계

상관관계는 증권 간의 관계를 측정하는 데 사용되는 통계 방법입니다. 이 정보는 히트맵을 사용하여 가장 잘 볼 수 있습니다. 히트맵을 사용하면 증권 간의 상관관계를 확인할 수 있습니다.

returns.plot_corr_heatmap()

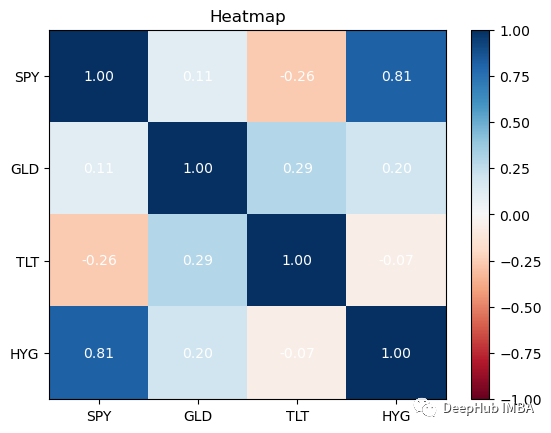
最好在你的投资组合中拥有相关性较低的资产。除了SPY与HYG，这四个资产类别的相关性都很低，这对我们的投资组合是不利的：因为如果拥有高度相关的不同资产组，即使你将风险分散在它们之间，从投资组合构建的角度来看，收益也会很少。

总结

通过分析和绘制的所有数据进行资产配置，可以建立一个投资组合，极大地改变基础投资的风险特征。还有很多我没有提到的，但可以帮助我们确定交易策略价值的起点。我们将在后续文章中添加更多的技术性能指标。

위 내용은 Python을 이용한 거래 전략 및 포트폴리오 분석의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!