산술 연산자 없이 Java에서 합계를 구현하는 방법

질문에 따르면 산술 연산자를 사용할 수 없으므로 논리 연산자와 시프트 연산자로만 시작할 수 있습니다.

우리는 ^(XOR) 연산이 두 숫자의 캐리 없는 합이라는 것을 알고 있습니다. 두 숫자를 더해도 캐리가 발생하지 않으면 그 합은 두 숫자의 합이 됩니다. 이것이 문제 해결의 열쇠입니다. 일반적으로 두 숫자를 더하면 캐리가 생성됩니다. 올바른 합계를 얻으려면 "캐리 없는 합"을 기준으로 캐리를 추가해야 합니다. 두 숫자의 해당 위치가 모두 1이면 캐리가 발생한다는 것을 알고 있습니다. 즉, 해당 위치 A&B==1이라는 조건에서 각 비트에 대한 캐리를 얻을 수 있지만 캐리는 추가하는 것입니다. 이 1을 해당 높은 숫자로 변환하므로 얻은 캐리를 왼쪽으로 한 자리 이동한 다음 이전에 얻은 "캐리 없는 합"에 추가하여 두 숫자의 합을 얻습니다.

우리는 여기서 무한한 마트료시카 인형을 만들 수 있음을 발견했습니다. "캐리 없는 합"과 "생성된 캐리"의 합을 구하려면 이 두 숫자를 각각 두 개의 새로운 숫자로 처리하고 합산하세요. 앞의 연산 역시 두 숫자가 캐리를 생성할 수 없을 때까지 반복되며, ^ 연산을 통해 직접 결과를 얻을 수 있습니다.

23 + 16의 값을 찾았다고 가정해 보세요.

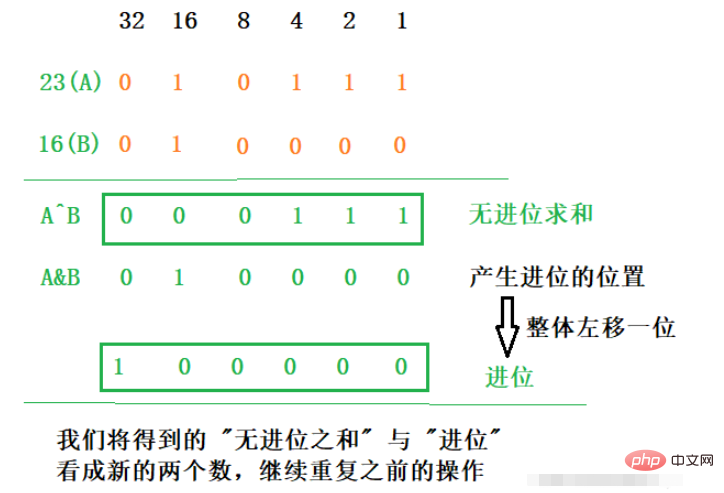
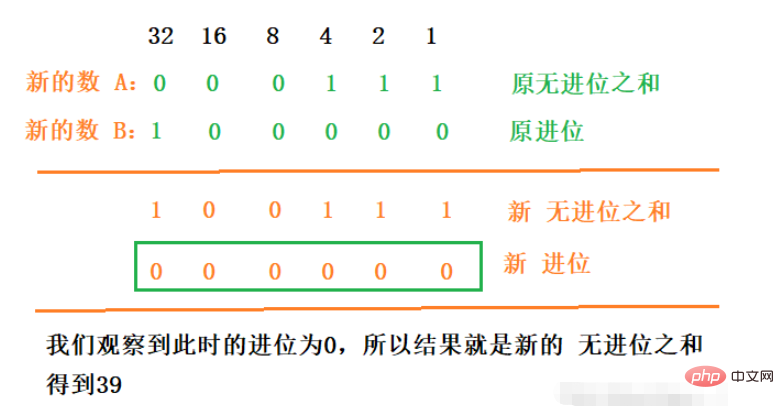
위의 아이디어에 따라 쉽게 코드를 작성할 수 있습니다

public static int addAB(int A, int B) {
		// 当两数的产生的进位为 0,就退出循环，返回其无进位和，就是结果
        while ((A & B) != 0) {
            int A_B = A ^ B;// 无进位求和
            int AB = (A & B) << 1;// 得到进位
            // 接下来就是求 得到的进位 + 无进位之和，重复前面的操作，直到不产生进位
            A = A_B;
            B = AB;
        }
        // 最后返回新的无进位之和
        return (A ^ B);
    }

그래서 그 정확성을 확인하기 위해 여기에 대수 변환기를 사용하고 함수는 ’

public static void main(String[] args) {
    int count = 1_0000_0000;// 比较次数 100000000次
    Random random = new Random();// 生成随机数字
    boolean flag = true;// 相等则为 true

    for (int i = 0; i < count; i++) {
        int num1 = random.nextInt(Integer.MAX_VALUE/2);// 随机正数1
        int num1_2 = random.nextInt(Integer.MAX_VALUE/2);// 随机正数2
        // 随机正数1 + 随机正数2
        if ((num1+num1_2) != addAB(num1,num1_2)){
            // 有一次不相等的，则退出循环
            flag = false;
            break;
        }

        int num2 = -random.nextInt(Integer.MAX_VALUE/2);// 随机负数1
        int num2_2 = -random.nextInt(Integer.MAX_VALUE/2);// 随机负数2
        // 随机负数1  + 随机负数2
        if ((num2+num2_2) != addAB(num2,num2_2)){
            // 有一次不相等的，则退出循环
            flag = false;
            break;
        }

        int num3 = random.nextInt(Integer.MAX_VALUE);// 随机正数
        int num4 = -random.nextInt(Integer.MAX_VALUE);// 随机负数
        // 随机正数  + 随机负数
        if ((num3+num4) != addAB(num3,num4)){
            // 有一次不相等的，则退出循环
            flag = false;
            break;
        }
    }
    System.out.println(flag);
}

실행 결과:

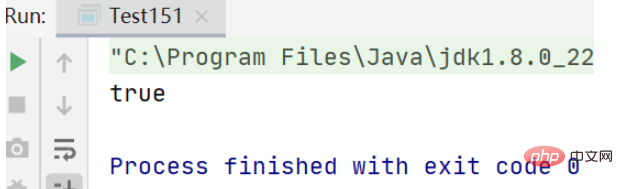
최종 출력 결과는 true입니다. 즉, 무작위로 생성된 양수+양수, 음수+음수, 양수+음수를 각각 100000000번 계산한 결과가 나왔습니다. 오류가 한 번도 발생하지 않았으며 이는 해당 기능이 신뢰할 수 있음을 나타냅니다.

위 내용은 산술 연산자 없이 Java에서 합계를 구현하는 방법의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!