Java의 Union-Find 분석 예

1. 개요

Union-find: 서로소 집합의 일부 병합 및 쿼리 문제를 해결하는 데 사용되는 트리 유형 데이터 구조입니다. 예: n개의 마을이 있고, 두 마을 사이에 연결 도로가 있는지 쿼리하여 두 마을을 연결합니다.

두 코어:

Find(Find): 요소가 위치한 집합 찾기

Union(Union) : 두 개를 결합합니다 요소 집합이 하나의 집합으로 병합됩니다

2.

Union 검색 구현 두 가지 일반적인 구현 아이디어가 있습니다

Quick Find

• Find의 시간 복잡도: O(1)

• Time Union의 복잡도: O(n)

Quick Union

• Find의 시간 복잡도: O(logn)은 O(a (n))a(n)

• Time으로 최적화될 수 있습니다. Union의 복잡성: O(logn)은 배열을 사용하여 O(a(n))a(n)

로 최적화될 수 있습니다. 배열의 첨자는 요소이고 값은 배열은 상위 노드의 값입니다

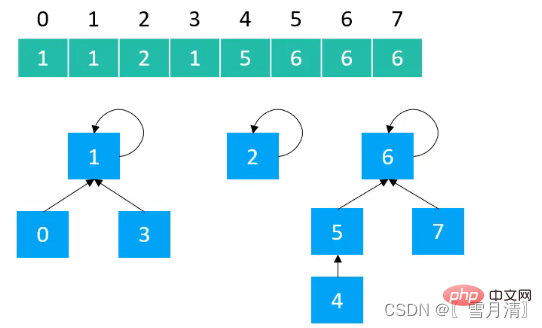
추상 클래스 생성 Union Find

public abstract class UnionFind {
 
	 int[] parents;
	/**
	 * 初始化并查集
	 * @param capacity
	 */
	public UnionFind(int capacity){
		
		if(capacity < 0) {
			throw new IllegalArgumentException("capacity must be >=0");
		}
        //初始时每一个元素父节点（根结点）是自己
		parents = new int[capacity];
		for(int i = 0; i < parents.length;i++) {
			parents[i] = i;
		}
	}
	
   /**
     *  检查v1 v2 是否属于同一个集合
     */
	public boolean isSame(int v1,int v2) {
		return find(v1) == find(v2);
	}
 
    /**
     *  查找v所属的集合 （根节点）
     */
	public  abstract int find(int v);
 
	/**
     *  合并v1 v2 所属的集合
     */
	public abstract void union(int v1, int v2);
	
		
	// 范围检查
	public   void rangeCheck(int v)  {
		if(v<0 || v > parents.length)
			throw new IllegalArgumentException("v is out of capacity");
	}
}

2.1 Quick Find 구현

Quick Find로 구현된 Union 검색, 트리 최대 높이는 2이며, 각 노드의 상위 노드 는 루트 노드입니다

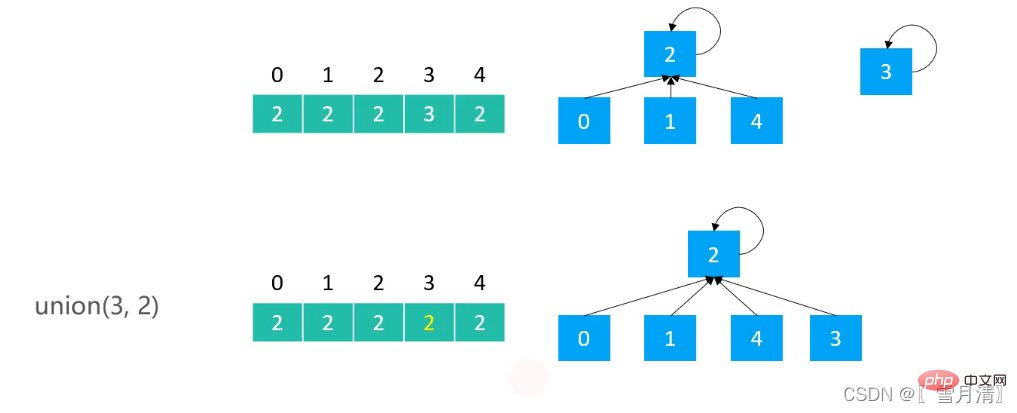
public class UnionFind_QF extends UnionFind {
	public UnionFind_QF(int capacity) {
		super(capacity);
		
	}
 
  // 查
@Override
	public  int  find(int v) {
		rangeCheck(v);
		return parents[v];
	}
 
 // 并 将v1所在集合并到v2所在集合上
@Override
public void union(int v1, int v2) {
    // 查找v1 v2 的父（根）节点
	int p1= find(v1);
	int p2 = find(v2);
	if(p1 == p2) return;
  
    //将所有以v1的根节点为根节点的元素全部并到v2所在集合上 即父节点改为v2的父节点
	for(int i = 0; i< parents.length; i++) {
		if(parents[i] == p1) {
			parents[i] = p2;
		}
	}
	
  }
}

2.2 Quick Union 구현

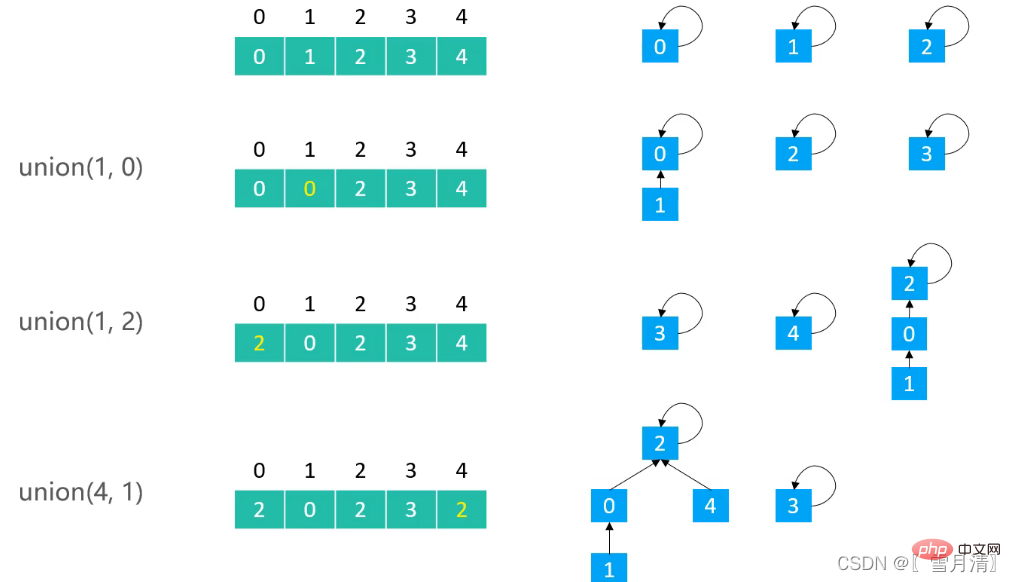
public class UnionFind_QU extends UnionFind {
 
	public UnionFind_QU(int capacity) {
		super(capacity);
		
	}
 
	//查某一个元素的根节点
	@Override
	public int find(int v) {
   //检查下标是否越界
		rangeCheck(v);
   
  // 一直循环查找节点的根节点
		while (v != parents[v]) {
			v = parents[v];
		}
		return v;
	}
 
//V1 并到 v2 中
	@Override
	public void union(int v1, int v2) {
	
		int p1 = find(v1);
		int p2 = find(v2);
		if(p1 == p2) return;
      //将v1 根节点 的 父节点 修改为 v2的根结点 完成合并
		parents[p1] = p2;
	}
}

3. 최적화

Union 조회는 Quick Union으로 구현되는 경우가 많지만 때로는 트리가 불균형할 때 Quick Union을 구현하는 경우도 있습니다

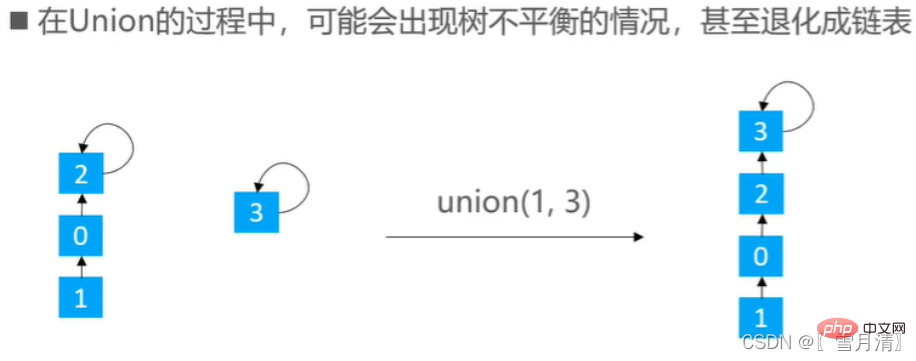
있습니다. 두 가지 최적화 아이디어: 순위 최적화와 크기 최적화

3.1 크기 기반 최적화

핵심 아이디어: 요소가 적은 트리를 요소가 많은 트리에 접목합니다

public class UniondFind_QU_S extends UnionFind{
 
   // 创建sizes 数组记录 以元素（下标）为根结点的元素（节点）个数
	private int[] sizes;
 
	public UniondFind_QU_S(int capacity) {
		super(capacity);
 
		sizes = new int[capacity];
 
   //初始都为 1
		for(int i = 0;i < sizes.length;i++) {
			sizes[i] = 1;
			}
		
	}
 
	@Override
	public int find(int v) {
 
		rangeCheck(v);
 
		while (v != parents[v]) {
			v = parents[v];
		}
		return v;
	}
 
	@Override
	public void union(int v1, int v2) {
	
		int p1 = find(v1);
		int p2 = find(v2);
		if(p1 == p2) return;
 
		//如果以p1为根结点的元素个数 小于 以p2为根结点的元素个数 p1并到p2上，并且更新p2为根结点的元素个数
	if(sizes[p1] < sizes[p2]) {
		    parents[p1] = p2;
		    sizes[p2] += sizes[p1];
		
 // 反之 则p2 并到 p1 上，更新p1为根结点的元素个数
	}else {
			parents[p2] = p1;
			sizes[p1] += sizes[p2];
		}
	}
}

크기 기반 최적화 트리의 불균형을 초래할 수도 있습니다

3.2 순위 기반 최적화

핵심 아이디어: 키가 큰 나무에 짧은 나무를 접목

public class UnionFind_QU_R extends UnionFind_QU {
   // 创建rank数组  ranks[i] 代表以i为根节点的树的高度
 private int[] ranks;
 
	public UnionFind_QU_R(int capacity) {
		super(capacity);
 
		ranks = new int[capacity];
 
		for(int i = 0;i < ranks.length;i++) {
			ranks[i] = 1;
		}
 
	}
    
	public void union(int v1, int v2) {
 
		int p1 = find(v1);
		int p2 = find(v2);
		if(p1 == p2) return;
    
    // p1 并到 p2 上 p2为根 树的高度不变
		if(ranks[p1] < ranks[p2]) {
			parents[p1] = p2;
			
  // p2 并到 p1 上 p1为根 树的高度不变
		} else if(ranks[p1] > ranks[p2]) {
			parents[p2] = p1;
 
		}else {
    // 高度相同 p1 并到 p2上，p2为根 树的高度+1
			parents[p1] = p2;
			ranks[p2] += 1;
		}
	}
}

순위 최적화에 따라 Union 수가 증가할수록 트리 높이가 계속해서 높아집니다. 찾기 작업이 발생합니다. 속도를 늦추려면

최적화를 계속하는 세 가지 아이디어가 있습니다: 경로 압축, 경로 분할 및 경로 절반

3.2.1 경로 압축(Path Compression)

찾을 때 경로의 모든 노드가 루트 노드를 가리키도록 만듭니다. 트리 높이 줄이기

/**
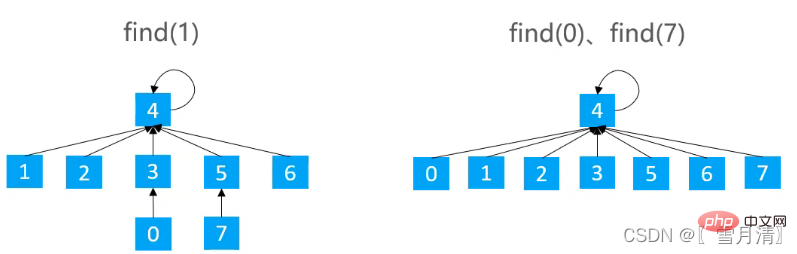
 *  Quick Union -基于rank的优化  -路径压缩
 *
 */
public class UnionFind_QU_R_PC extends UnionFind_QU_R {
 
	public UnionFind_QU_R_PC(int capacity) {
		super(capacity);
		
	}
 
	@Override
	public int find(int v) {
		rangeCheck(v);
 
		if(parents[v] != v) {
 
        //递归 使得从当前v 到根节点 之间的 所有节点的 父节点都改为根节点
			parents[v] = find(parents[v]);
		}
		return parents[v];
	}
}

트리 높이를 줄일 수는 있지만 구현 비용은 약간 더 높습니다.

3.2.2 경로 분할(Path Spliting)

경로의 모든 노드가 해당 노드를 가리키도록 만듭니다. 조부모 노드

/**
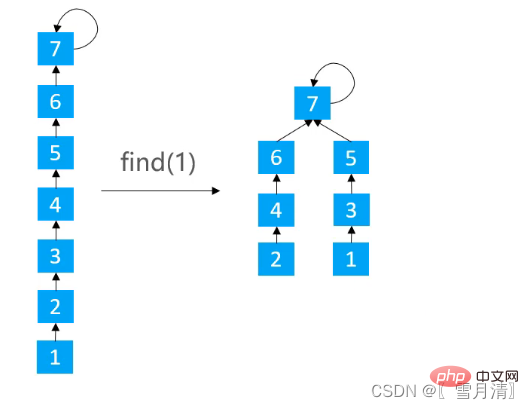
 *  Quick Union -基于rank的优化  -路径分裂
 *
 */
public class UnionFind_QU_R_PS extends UnionFind_QU_R {
 
	public UnionFind_QU_R_PS(int capacity) {
		super(capacity);
		
	}
 
	@Override
	public int find(int v) {
		rangeCheck(v);
		while(v != parents[v]) {
 
			int p = parents[v];
			parents[v] = parents[parents[v]];
			v = p;
		}
		return v;
	}
}

3.2.3 경로 분할

경로의 다른 모든 노드가 조부모 노드를 가리키도록 만드세요

/**
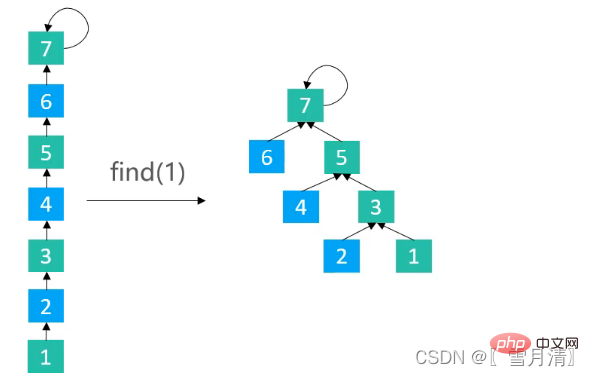
 *  Quick Union -基于rank的优化  -路径减半
 *
 */
public class UnionFind_QU_R_PH extends UnionFind_QU_R {
 
	public UnionFind_QU_R_PH(int capacity) {
		super(capacity);
		
	}
	
	
    public int find(int v) {
    	rangeCheck(v);
 
		while(v != parents[v]) {
			parents[v] = parents[parents[v]];
			v = parents[v];
		}
		return v;
	}	 
 }

Quick Union + 순위 기반 최적화 + 경로 분할 또는 경로 분할 사용

It 각 연산의 상각 시간 복잡도는 O(a(n)), a(n)

위 내용은 Java의 Union-Find 분석 예의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!