Google의 연구는 수학적 문제를 코드로 변환함으로써 기계 증명의 정확성을 크게 향상시켰습니다.
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWB앞으로
- 2023-04-27 17:01:07973검색
컴퓨터는 한동안 수학적 증명을 검증하는 데 사용되었지만 특별히 고안된 증명 언어를 사용하여 문제를 준비하는 경우에만 컴퓨터를 사용할 수 있으며 수학자가 사용하는 수학적 표기법과 문자 텍스트의 혼합을 처리할 수 없습니다.
자연어로 작성된 수학 문제를 형식 코드로 변환하고 컴퓨터가 더 쉽게 풀 수 있도록 하면 수학의 새로운 발견을 탐구할 수 있는 기계를 만드는 데 도움이 될 수 있습니다.
이 과정을 형식화라고 하는데, 하나의 증명만으로도 수년이 걸릴 수 있으므로 수학적 지식의 극히 일부만 형식화되고 기계에 의해 증명됩니다.
자동정식화란 수학을 자연어에서 형식언어로 자동으로 번역하는 작업을 의미합니다. 성공적인 자동화된 형식화 도구의 실용적이고 철학적인 의미는 엄청날 것이며, 현재의 과도한 형식화 비용을 줄일 수 있으며, 장기적으로는 다양한 연구 분야에서 수학적 추론의 자동화된 측면을 연결할 수 있습니다.
최근 연구에서 Google의 Yuhuai Wu와 그의 공동 작업자는 OpenAI Codex의 신경망을 사용하여 형식화 작업을 자동화했습니다. Codex는 웹의 대량 텍스트 및 프로그래밍 데이터에 대해 교육을 받았으며 프로그래머는 이를 사용하여 신뢰할 수 있는 코드를 생성할 수 있습니다.

문서 링크: https://arxiv.org/pdf/2205.12615.pdf
12,500개의 중학교 수학 경쟁 문제 형식화
대형 언어 모델의 최근 발전은 형식 언어를 이해하는 모델의 능력을 보여줍니다. 잠재적인. 그러나 기존의 성공은 웹에 대규모 말뭉치가 존재하는 공식 언어(예: Python)로 제한되었습니다. 이에 반해, 공식 수학 데이터는 매우 부족합니다. 가장 큰 공식 수학 언어 라이브러리 중 하나인 Archive of Formal Proofs의 크기는 180mb에 불과하며 이는 대규모 언어 모델 Codex의 훈련 데이터의 0.18%에도 미치지 못합니다.
게다가 자연어 독스트링이 널리 사용되는 범용 프로그래밍 언어의 경우와 달리 자연어와 형식적 수학 언어 사이에는 데이터 정렬이 거의 없습니다. 따라서 대규모 언어 모델의 성공이 자동 형식화의 개발을 직접적으로 촉진할 수 있는지는 아직 알 수 없습니다.
증명 언어와 프로그래밍 언어의 유사성을 고려하여 팀은 Codex가 12,500개의 중학교 수학 경시 문제 라이브러리를 공식화할 수 있는지 알아보기로 결정했습니다. 문제의 4분의 1을 형식 증명 해결사인 Isabelle과 호환되는 형식으로 변환할 수 있습니다.
Wu는 많은 성공적인 변환이 시스템이 특정 수학적 개념을 이해하지 못한 결과라고 말했습니다. “개념을 설명하는 예를 통해 모델을 보여주면 모델이 빠르게 이해할 수 있습니다.”
이 작업에서는 대규모 언어 모델의 자동 형식화 가능성을 탐색합니다. 연구원들은 대규모 언어 모델이 이미 대화형에 있다는 것을 발견했습니다. 공식 정리 증명자는 자연어 수학을 형식화하는 데 매우 뛰어난 능력을 가지고 있습니다.
아래 그림 1은 자동 형식화의 완벽한 예입니다. 모델은 구문적으로 올바른 Isabelle 코드를 변환할 뿐만 아니라 자연어로 중요한 추론 포인트를 포착할 수도 있습니다.

이 자동화된 형식화 도구의 효율성을 테스트하기 위해 팀은 이미 인간 형식화 버전이 있는 일련의 문제에 Codex를 적용했으며, Codex는 자체 형식화 버전도 생성했습니다. 팀은 MiniF2F라는 또 다른 AI를 사용하여 두 가지 버전의 문제를 모두 해결했습니다.
문제를 자동으로 형식화하면 MiniF2F의 성공률이 29%에서 35%로 높아집니다. 이는 Codex가 문제 형식화에 중요한 진전을 이뤘음을 나타냅니다.
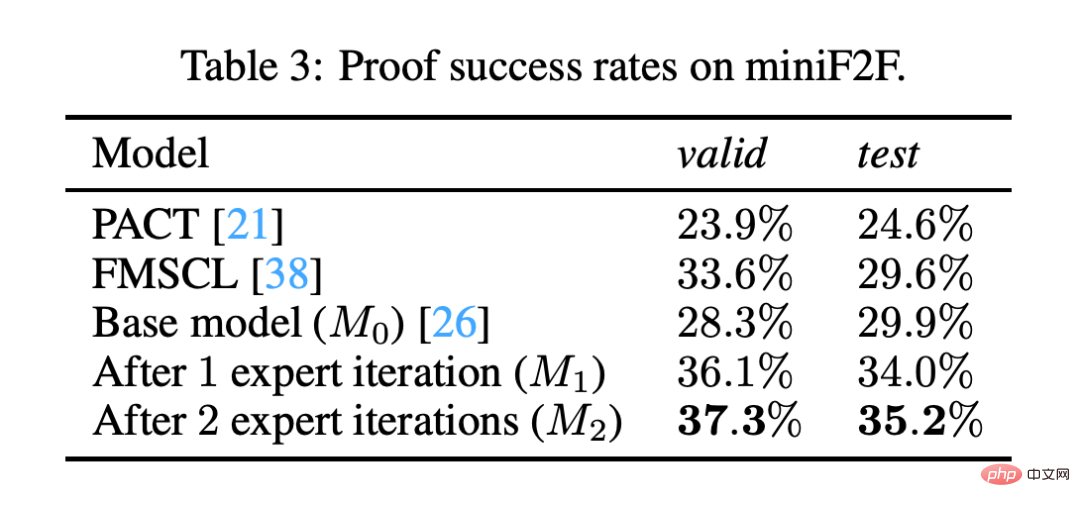
많은 수학 경시대회의 발표는 주어진 명제를 증명하기보다는 특정 질문에 대한 답을 찾는 형식인 경향이 있다는 점은 주목할 가치가 있습니다. 그러나 공식적인 수학적 진술은 질문이 아닌 명제의 형태입니다.
질문을 명제로 변환하기 위해 연구자는 질문 뒤에 "최종 답변"을 첨부했습니다.

자동 형식화에 사용되는 프롬프트 형식은 다음과 같습니다.

AI가 인간 수학과 경쟁하게 될까요?
이것은 흥미로운 전개이지만 Wu는 팀의 작업은 단지 개념 증명일 뿐이라고 말했습니다. "최고의 인간 수학자에 필적하는 기계를 훈련시키는 것이 목표라면 자동 형식화가 이 목표를 달성하는 핵심 경로인 것 같습니다."
케임브리지 대학 팀의 일원인 Albert Jiang은 다음과 같이 말했습니다. 성공률이 더욱 향상되면 AI는 인간 수학자들이 경쟁하는 것과 경쟁할 수 있게 됩니다. "100%에 도달하면 반드시 국제수학올림피아드 금메달을 획득하는 AI 에이전트를 만들겠습니다."
팀의 당면 목표는 자동형식모형과 자동증명기를 개선하는 것이지만 연구결과의 미래는 그 영향은 광범위할 것이다. Wu는 이러한 모델이 현재 인간에게 알려지지 않은 수학 분야를 밝힐 수 있다고 말합니다.
이 기계의 추론 기능은 더 넓은 범위의 검증 작업에도 매우 적합합니다. "소프트웨어가 원하는 작업을 정확하게 수행하는지 확인할 수 있고, 하드웨어 칩을 검증하여 금융 거래 알고리즘과 하드웨어 설계 모두에 적용할 수 있습니다.
기계를 사용하여 수학을 탐구하는 것은 흥미로운 일입니다." 그러나 실제 과제는 대부분 LaTex로 작성된 수학적 연구에 모델을 사용하는 것이라고 런던 수리 과학 연구소의 Yang-Hui He는 말합니다. "우리는 LaTex를 사용하는 이유는 입력이 부드럽기 때문이지만 어떤 의미에서는 자연어이고 고유한 규칙이 있습니다."
LaTeX에서는 사용자가 자신만의 함수와 기호를 정의할 수 있기 때문에 이러한 함수와 기호는 다음과 같습니다. 하나의 수학 논문에만 사용될 수 있습니다. 이는 일반 텍스트로만 훈련된 신경망의 경우 까다로울 수 있습니다.
위 내용은 Google의 연구는 수학적 문제를 코드로 변환함으로써 기계 증명의 정확성을 크게 향상시켰습니다.의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!

