학습 = 피팅? 딥러닝과 고전적인 통계는 같은 것인가요?
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWB앞으로
- 2023-04-16 21:28:01768검색
이 기사에서 이론 컴퓨터 과학자이자 하버드 대학교의 저명한 교수인 보아즈 바라크(Boaz Barak)는 딥러닝과 고전 통계학의 차이점을 자세히 비교합니다. 그는 "딥러닝을 순수하게 통계적인 관점으로 이해한다면, 성공의 핵심 요소를 무시할 것입니다." ".
딥 러닝(또는 일반적으로 머신 러닝)은 단순히 통계라고 생각하는 경우가 많습니다. 즉, 기본적으로 통계학자가 연구하는 개념과 동일하지만 통계와는 다른 용어를 사용하여 설명합니다. Rob Tibshirani는 이 흥미로운 "어휘"를 아래에 요약한 적이 있습니다.

이 목록에 정말 공감되는 내용이 있나요? 머신러닝에 관련된 거의 모든 사람들은 Tibshiriani가 게시한 표 오른쪽에 있는 많은 용어가 머신러닝에서 널리 사용된다는 것을 알고 있습니다.
순전히 통계적 관점으로 딥러닝을 이해한다면 성공의 핵심 요소를 무시하게 될 것입니다. 딥러닝에 대한 보다 적절한 평가는 완전히 다른 개념을 설명하기 위해 통계적 용어를 사용한다는 것입니다.
딥러닝에 대한 올바른 평가는 오래된 통계 용어를 설명하기 위해 다른 단어를 사용하는 것이 아니라, 해당 용어를 사용하여 완전히 다른 프로세스를 설명한다는 것입니다.
이 기사에서는 딥 러닝의 기초가 실제로 통계와 다르거나 심지어 기존 머신 러닝과 다른 이유를 설명합니다. 이 문서에서는 먼저 모델을 데이터에 맞출 때 "설명" 작업과 "예측" 작업의 차이점을 설명합니다. 그런 다음 학습 과정의 두 가지 시나리오를 논의합니다. 1. 경험적 위험 최소화를 사용하여 통계 모델을 맞춤 2. 학생들에게 수학적 기술을 가르칩니다. 그런 다음 이 기사에서는 어떤 시나리오가 딥 러닝의 본질에 더 가까운지 논의합니다.
딥러닝을 위한 수학과 코드는 통계 모델을 피팅하는 것과 거의 동일합니다. 그러나 더 깊은 수준에서 보면 딥 러닝은 학생들에게 수학 기술을 가르치는 것과 비슷합니다. 그리고 감히 내가 딥러닝 이론을 완전히 마스터했다고 주장하는 사람은 거의 없을 것입니다. 실제로 그러한 이론이 존재하는지는 의심스럽다. 대신 딥 러닝의 다양한 측면은 다양한 관점에서 가장 잘 이해되며, 통계만으로는 완전한 그림을 제공할 수 없습니다.
이 글에서는 딥러닝과 통계를 비교합니다. 여기서 통계란 특별히 '고전 통계'를 지칭하는 이유는 가장 오랫동안 연구되어 교과서에 실려 있기 때문입니다. 20세기 물리학자들이 고전물리학의 틀을 확장해야 했던 것처럼, 많은 통계학자들이 딥러닝과 비고전적 이론 방법을 연구하고 있습니다. 실제로 컴퓨터 과학자와 통계학자 사이의 경계를 모호하게 만드는 것은 양측 모두에게 이익이 됩니다.
예측 및 모델 피팅
과학자들은 모델의 정확성을 검증하기 위해 항상 모델 계산 결과와 실제 관찰 결과를 비교해 왔습니다. 이집트의 천문학자 프톨레마이오스는 행성 운동에 대한 독창적인 모델을 제안했습니다. 프톨레마이오스의 모델은 지구중심설을 따랐지만 일련의 주전원(아래 이미지 참조)을 갖고 있어 뛰어난 예측 정확도를 제공합니다. 대조적으로, 코페르니쿠스의 원래 태양 중심 모델은 프톨레마이오스 모델보다 단순했지만 관측 예측에서는 정확성이 떨어졌습니다. (코페르니쿠스는 나중에 프톨레마이오스의 모델과 비교하기 위해 자신의 주전원을 추가했습니다.)
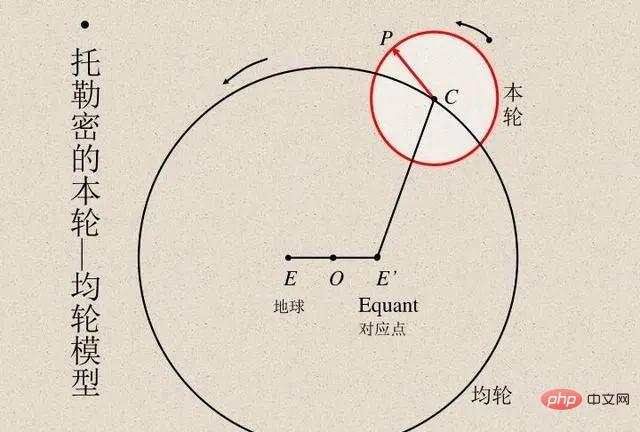
프톨레마이오스와 코페르니쿠스의 모델은 모두 비교할 수 없습니다. "블랙박스"를 통해 예측하고 싶다면 프톨레마이오스의 지구 중심 모델이 더 우수합니다. 그러나 "내부를 들여다볼" 수 있는 간단한 모델(항성 운동을 설명하는 이론의 출발점)을 원한다면 코페르니쿠스의 모델이 적합합니다. 나중에 케플러는 코페르니쿠스의 모형을 타원 궤도로 개량하고 케플러의 행성 운동 3법칙을 제안했는데, 이를 통해 뉴턴은 행성의 법칙을 지구에 적용할 수 있는 중력의 법칙으로 설명할 수 있었습니다.
따라서 태양 중심 모델은 단지 예측을 제공하는 "블랙 박스"가 아니라 몇 가지 간단한 수학 방정식으로 제공되지만 방정식에서 "움직이는 부분"이 거의 없다는 것이 중요합니다. 천문학은 수년 동안 통계 기술을 개발하는 데 영감의 원천이었습니다. 가우스와 르장드르는 소행성과 기타 천체의 궤도를 예측하기 위해 1800년경에 최소 제곱 회귀를 독립적으로 발명했습니다. 1847년에 Cauchy는 천문학적 예측에 영감을 받아 경사하강법을 발명했습니다.
물리학에서는 때때로 학자들이 "올바른" 이론을 찾고, 예측 정확도를 최적화하고, 데이터를 가장 잘 해석할 수 있는 모든 세부 정보를 갖고 있습니다. 이는 단순성, 예측력, 설명력이 모두 조화를 이룬다고 가정한 오컴의 면도날과 같은 사상의 범위에 속한다.
그러나 다른 많은 분야에서는 설명과 예측이라는 두 가지 목표 사이의 관계가 그다지 조화롭지 않습니다. 단지 관찰 결과를 예측하고 싶다면 "블랙박스"를 통과하는 것이 가장 좋습니다. 반면, 인과관계 모델, 일반 원리, 중요한 특징 등 설명 정보를 얻으려면 이해하고 설명할 수 있는 모델이 단순할수록 좋습니다.
올바른 모델 선택은 목적에 따라 다릅니다. 예를 들어, 많은 개인(예: 일부 질병)의 유전적 발현과 표현형이 포함된 데이터세트를 생각해 보세요. 목표가 사람의 질병 가능성을 예측하는 것이라면 그것이 얼마나 복잡하든지 얼마나 많은 유전자에 의존하든 상관없습니다. , 작업에 적합한 최상의 예측 모델을 사용합니다. 반대로, 추가 연구를 위해 몇 가지 유전자를 식별하는 것이 목적이라면 복잡하고 매우 정확한 "블랙 박스"는 사용이 제한됩니다.
통계학자 Leo Breiman은 2001년 통계 모델링의 두 문화에 관한 유명한 기사에서 이 점을 지적했습니다. 첫 번째는 데이터를 설명할 수 있는 단순한 생성 모델에 초점을 맞춘 '데이터 모델링 문화'입니다. 두 번째는 데이터가 어떻게 생성되었는지에 대해 불가지론적이고, 아무리 복잡하더라도 데이터를 예측할 수 있는 모델을 찾는 데 중점을 두는 '알고리즘 모델링 문화'입니다.

논문 제목:
Statistical Modeling: The Two Cultures
논문 링크:
https://projecteuclid.org/euclid.ss/1009213726
Breiman은 통계가 첫 번째 문화의 영향을 너무 많이 받는다고 믿습니다. , 이러한 초점은 두 가지 문제를 야기합니다.
- 관련 없는 이론과 의심스러운 과학적 결론으로 이어집니다.
- 통계학자가 흥미롭고 새로운 질문을 연구하는 것을 방해합니다.
Breiman의 논문이 나오자마자 일부 논란이 발생했습니다. 동료 통계학자인 브래드 에프론(Brad Efron)은 일부 요점에는 동의하지만 브라이먼의 주장은 복잡한 "블랙 박스"를 만들기 위해 많은 노력을 기울이는 과학적 통찰력과 검소함에 반대되는 것 같다고 강조했습니다. 그러나 최근 기사에서 Efron은 자신의 이전 견해를 포기하고 "21세기 통계의 초점은 Breiman이 제안한 노선을 따라 크게 발전한 예측 알고리즘에 있기 때문에" Breima가 더 예지력이 있다는 점을 인정했습니다.
고전 및 현대 예측 모델
딥 러닝이든 아니든 머신러닝은 예측에 초점을 맞춘 Breiman의 두 번째 관점을 따라 발전해 왔습니다. 이 문화는 오랜 역사를 가지고 있습니다. 예를 들어, 1973년에 출판된 Duda와 Hart의 교과서와 Highleyman의 1962년 논문에서는 아래 그림의 내용을 기술했는데, 이는 오늘날 딥러닝 연구자들이 매우 이해하기 쉽습니다.

Duda and Hart 교과서 "패턴 분류"에서 발췌 및 장면 분석" 및 Highleyman의 1962년 논문 "패턴 인식 실험의 설계 및 분석"이 있습니다.
마찬가지로 아래의 Highleyman 손글씨 문자 데이터세트와 이에 맞게 사용된 아키텍처 이미지인 Chow(1962)(정확도 ~58%)는 많은 사람들의 공감을 불러일으킬 것입니다.

딥러닝은 왜 다른가요?
1992년 Geman, Bienenstock 및 Doursat는 신경망에 대한 비관적인 기사를 작성하여 "현재의 피드포워드 신경망은 기계 인식 및 기계 학습의 어려운 문제를 해결하기에는 대체로 불충분합니다."라고 주장했습니다. 특히 그들은 범용 신경망이 어려운 작업을 처리하는 데 성공하지 못할 것이며, 성공할 수 있는 유일한 방법은 인위적으로 설계된 기능을 통해서만 가능하다고 주장합니다. 그들의 말에 따르면: "중요한 속성은 통계적 의미에서 학습되기보다는 내장되거나 "내장"되어 있어야 합니다." 이제 Geman et al.은 완전히 틀린 것처럼 보이지만 이해하는 것이 더 흥미롭습니다. 왜 그들이 틀렸는지.
딥러닝은 다른 학습 방법과는 확실히 다릅니다. 딥 러닝은 최근접 이웃이나 랜덤 포레스트처럼 단순한 예측처럼 보일 수도 있지만 더 복잡한 매개변수를 가질 수도 있습니다. 이는 질적인 차이보다는 양적인 차이인 것으로 보인다. 그러나 물리학에서는 규모가 몇 자릿수만큼 변하면 완전히 다른 이론이 필요한 경우가 많으며 딥러닝에서도 마찬가지입니다. 딥 러닝과 클래식 모델(파라메트릭 또는 비파라메트릭)의 기본 프로세스는 완전히 다르지만 수학 방정식(및 Python 코드)은 높은 수준에서 동일합니다.
이 점을 설명하기 위해 통계 모델을 적용하고 학생들에게 수학을 가르치는 두 가지 시나리오를 고려해 보세요.
시나리오 A: 통계 모델 피팅
데이터를 통해 통계 모델을 피팅하는 일반적인 단계는 다음과 같습니다.
1. 여기에 일부 데이터가 있습니다  (
( 는
는  의 행렬이고
의 행렬이고  는
는  차원 벡터입니다. 즉, 카테고리 라벨입니다. 데이터가 구조가 있고 노이즈가 포함된 모델, 즉 장착할 모델에서 나오는 것으로 생각하세요.)
차원 벡터입니다. 즉, 카테고리 라벨입니다. 데이터가 구조가 있고 노이즈가 포함된 모델, 즉 장착할 모델에서 나오는 것으로 생각하세요.)
2. 위의 데이터를 사용하여 모델을 피팅하고 최적화 알고리즘을 사용하여 경험적 위험을 최소화합니다. 즉, 최적화 알고리즘을 통해
최적화 알고리즘을 사용하여 경험적 위험을 최소화합니다. 즉, 최적화 알고리즘을 통해  가 가장 작고,
가 가장 작고, 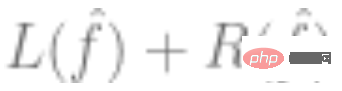 가 손실(예측 값이 실제 값에 얼마나 가까운지 나타냄)을 나타내고,
가 손실(예측 값이 실제 값에 얼마나 가까운지 나타냄)을 나타내고,  가 선택적 정규화 항이 되도록 이러한
가 선택적 정규화 항이 되도록 이러한  을 찾습니다.
을 찾습니다.
3. 모델의 전체 손실이 작을수록 좋습니다. 즉, 일반화 오류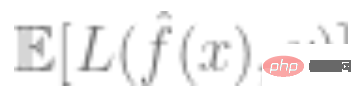 의 값이 상대적으로 최소화됩니다.
의 값이 상대적으로 최소화됩니다.
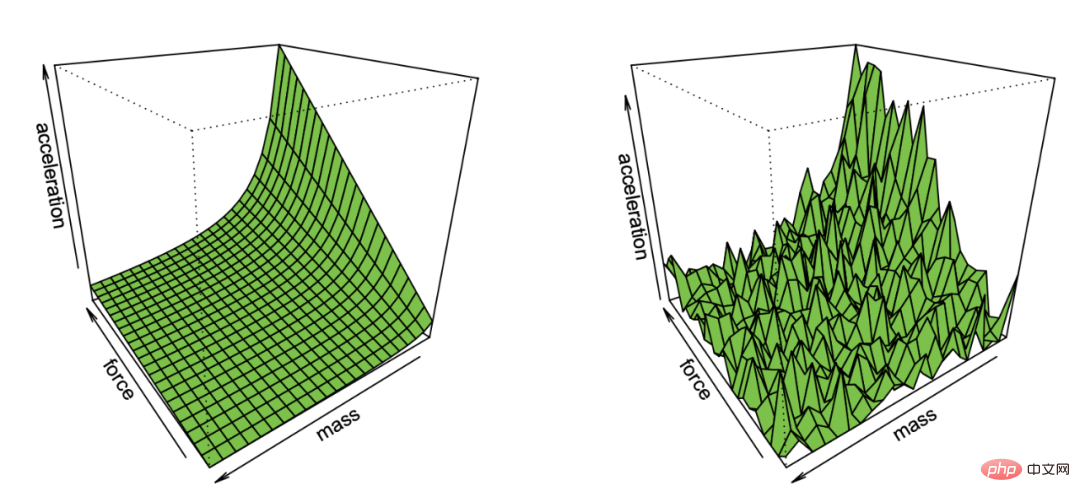
노이즈가 포함된 관찰에서 뉴턴의 제1법칙을 복구하는 Effron의 그림
이 매우 일반적인 예에는 실제로 최소 제곱 선형 회귀, 최근접 이웃, 신경망 훈련 등 많은 내용이 포함되어 있습니다. 고전적인 통계 시나리오에서는 일반적으로 다음과 같은 상황에 직면합니다.
절충점: 최적화된 모델 집합이라고 가정합니다(함수가 볼록하지 않거나 정규화 항을 포함하는 경우 신중하게 선택한 알고리즘 및 정규화로 인해 다음이 발생할 수 있음). 편향은 요소가 달성할 수 있는 실제 값에 가장 가까운 근사치입니다. 세트가 클수록 편향은 작아지며 0이 될 수 있습니다(출력 모델의 분산이 클수록). 전반적인 일반화 오류는 편향과 분산의 합입니다. 따라서 통계적 학습은 일반적으로 편향-분산 균형이며, 올바른 모델 복잡성은 전체 오류를 최소화하는 것입니다. 그들은 신경망에 대한 비관적인 태도를 다음과 같이 주장합니다. 편향-분산 딜레마는 신경망을 포함한 모든 비모수적 추론 모델에 적용됩니다.
"더 많은 것이 더 좋다"는 것이 항상 유지되는 것은 아닙니다. 예를 들어, 통계 학습에서는 기능이나 데이터가 반드시 더 많은 성능을 향상시키는 것은 아닙니다. 관련 없는 특성이 많이 포함된 데이터에서 학습하기 어렵습니다. 마찬가지로 데이터가 두 분포(예: 및 ) 중 하나에서 나오는 혼합 모델에서 학습하는 것은 어렵습니다.
수익률 감소. : 많은 경우 예측 노이즈를 수준으로 줄이는 데 필요한 데이터 포인트 수는 매개변수 및 와 관련이 있습니다. 즉, 데이터 포인트 수는 시작하는 데 약 k 샘플이 필요하지만 일단 그렇게 하면 즉, 90% 정확도에 도달하는 데 k 포인트가 필요한 경우 정확도를 95%로 높이려면 약 k 포인트가 추가로 필요합니다. 일반적으로 리소스가 증가하면(데이터, 모델 복잡성 또는 계산 여부에 관계없이) 원하는 결과를 얻을 수 있습니다. 특정 새로운 기능을 잠금 해제하는 대신 점점 더 미세한 구분
손실, 데이터에 대한 의존도 높음: 모델을 고차원 데이터에 맞출 때 작은 세부 사항은 말할 것도 없이 L1 또는 L2 정규화 프로그램 선택에 큰 차이를 만들 수 있습니다. 완전히 다른 수의 고차원 최적화 프로그램을 사용합니다. 또한 서로 매우 다릅니다.
데이터는 상대적으로 "순진"합니다. 일반적으로 데이터는 결정에 가깝지만 일부 분포와 독립적으로 샘플링된다고 가정합니다. 고차원에서의 측정 집중 현상을 고려하면 대부분의 점의 거리가 유사하다고 볼 수 있습니다. 따라서 고전적인 데이터 분포에서는 데이터 점 간의 거리 차이가 크지 않습니다. 혼합 모델에서는 이러한 차이가 나타날 수 있으므로 위에서 언급한 다른 문제와는 달리 이 차이는 통계에서 흔히 발생합니다.
시나리오 B: 수학 학습
이 시나리오에서는 학생들에게 수학(미분 계산 등)을 가르치고 싶다고 가정합니다. ) 일부 지침과 연습을 통해 이 시나리오는 몇 가지 질적 특성이 있습니다.
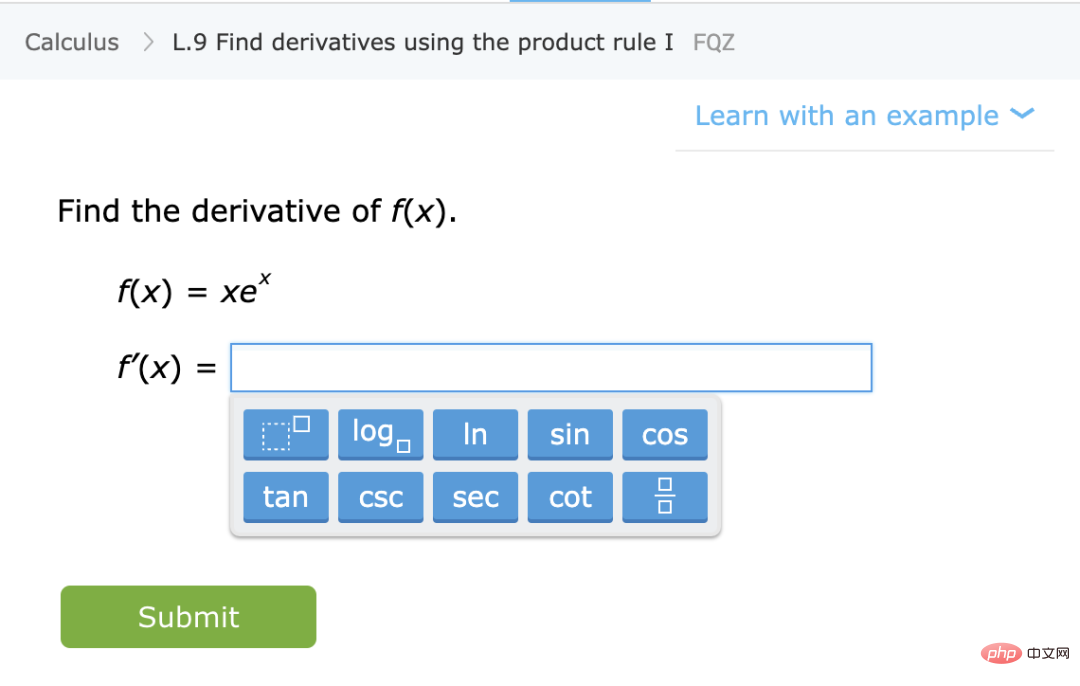 통계 분포를 근사화하는 대신 기술을 학습합니다. 이 경우 학생들은 추정/예측이 아닌 기술을 학습합니다. , 연습 문제를 해결 방법으로 매핑하는 기능이 알려지지 않은 특정 과제를 해결하기 위한 "블랙 박스"로 사용될 수 없더라도 이러한 문제를 해결할 때 학생들이 형성하는 사고 패턴은 여전히 알려지지 않은 과제에 유용합니다.
통계 분포를 근사화하는 대신 기술을 학습합니다. 이 경우 학생들은 추정/예측이 아닌 기술을 학습합니다. , 연습 문제를 해결 방법으로 매핑하는 기능이 알려지지 않은 특정 과제를 해결하기 위한 "블랙 박스"로 사용될 수 없더라도 이러한 문제를 해결할 때 학생들이 형성하는 사고 패턴은 여전히 알려지지 않은 과제에 유용합니다.
많을수록 좋습니다. 일반적으로 더 많은 질문을 하고 더 넓은 범위의 질문 유형을 다루는 학생들의 성적이 더 좋습니다. 일부 미적분학 및 대수학 문제를 동시에 푸는 것은 학생의 미적분학 점수 하락으로 이어지지는 않지만 미적분학 점수를 향상시키는 데 도움이 될 수 있습니다.
능력 향상부터 자동화된 표현까지: 어떤 경우에는 문제 해결에 대한 수익이 감소하기는 하지만 학생들은 여러 단계를 통해 학습합니다. 몇 가지 문제를 해결하면 개념을 이해하고 새로운 능력을 발휘하는 데 도움이 되는 단계가 있습니다. 또한, 학생들이 특정 유형의 문제를 반복할 때 비슷한 문제가 나타나면 자동화된 문제 해결 프로세스를 형성하여 이전의 능력 향상에서 자동 문제 해결로 전환됩니다.
데이터 및 손실과 무관한 성능: 수학적 개념을 가르치는 방법은 여러 가지가 있습니다. 서로 다른 책, 교육 방법, 채점 시스템을 사용하여 공부하는 학생들은 결국 동일한 내용을 배우고 비슷한 수학적 능력을 갖게 될 수 있습니다.
어떤 문제는 더 어렵습니다. 수학 연습에서 우리는 종종 서로 다른 학생들이 동일한 문제를 해결하는 방법 사이에 강한 상관관계가 있음을 볼 수 있습니다. 문제에는 고유한 난이도가 있고, 학습에 가장 적합한 난이도의 자연스러운 진행이 있는 것 같습니다.
딥러닝은 통계적 추정이나 학생의 학습 능력에 더 가깝나요?
위의 두 가지 비유 중 현대 딥러닝을 설명하는 데 더 적합한 것은 무엇입니까? 구체적으로 무엇이 성공하게 만들었나요? 통계적 모델 피팅은 수학과 코드를 사용하여 잘 표현될 수 있습니다. 실제로 표준 Pytorch 훈련 루프는 경험적 위험 최소화를 통해 심층 네트워크를 훈련합니다.

더 깊은 수준에서는 이 두 시나리오 간의 관계가 명확하지 않습니다. 좀 더 구체적으로 말하자면, 구체적인 학습 과제를 예로 들어 보겠습니다. "자기 지도 학습 + 선형 감지" 접근 방식을 사용하여 훈련된 분류 알고리즘을 생각해 보세요. 구체적인 알고리즘 훈련은 다음과 같습니다:
1. 데이터가 시퀀스라고 가정합니다. 여기서  는 특정 데이터 포인트(예: 그림)이고 레이블입니다.
는 특정 데이터 포인트(예: 그림)이고 레이블입니다.
2. 먼저 함수를 나타내는 심층 신경망을 얻습니다 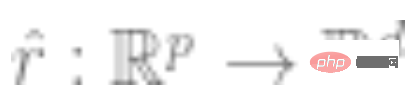 . 일부 유형의 자기 감독 손실 함수는 레이블이 아닌 데이터 포인트만 사용하여 최소화하여 학습됩니다. 이러한 손실 함수의 예로는 재구성(입력을 다른 입력으로 복원) 또는 대조 학습(핵심 아이디어는 특징 공간에서 양성 샘플과 음성 샘플을 비교하여 샘플의 특징 표현을 학습하는 것입니다)이 있습니다.
. 일부 유형의 자기 감독 손실 함수는 레이블이 아닌 데이터 포인트만 사용하여 최소화하여 학습됩니다. 이러한 손실 함수의 예로는 재구성(입력을 다른 입력으로 복원) 또는 대조 학습(핵심 아이디어는 특징 공간에서 양성 샘플과 음성 샘플을 비교하여 샘플의 특징 표현을 학습하는 것입니다)이 있습니다.
3. 교차 엔트로피 손실을 최소화하기 위해 완전한 레이블이 지정된 데이터를 사용하여 선형 분류기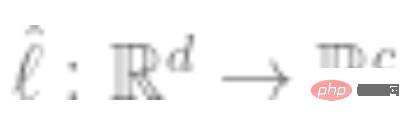 (클래스 수)를 맞춥니다. 최종 분류자는 다음과 같습니다.
(클래스 수)를 맞춥니다. 최종 분류자는 다음과 같습니다.
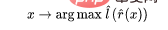
3단계는 선형 분류자에만 작동하므로 "마법"은 2단계(심층 네트워크의 자기 지도 학습)에서 발생합니다. 자기 지도 학습에는 몇 가지 중요한 속성이 있습니다:
함수를 근사화하는 대신 기술을 배우십시오. 자기 지도 학습은 함수를 근사화하는 것이 아니라 다양한 다운스트림 작업에 사용할 수 있는 표현을 학습하는 것입니다(이것은 자연어 처리의 지배적인 패러다임) . 선형 프로빙, 미세 조정 또는 여기를 통해 다운스트림 작업을 얻는 것은 부차적인 것입니다.
더 즐거울수록: 자기 지도 학습에서는 데이터 양이 늘어날수록 표현 품질이 향상되며, 여러 소스의 데이터를 혼합해도 표현 품질이 악화되지 않습니다. 사실 데이터는 다양할수록 좋습니다.
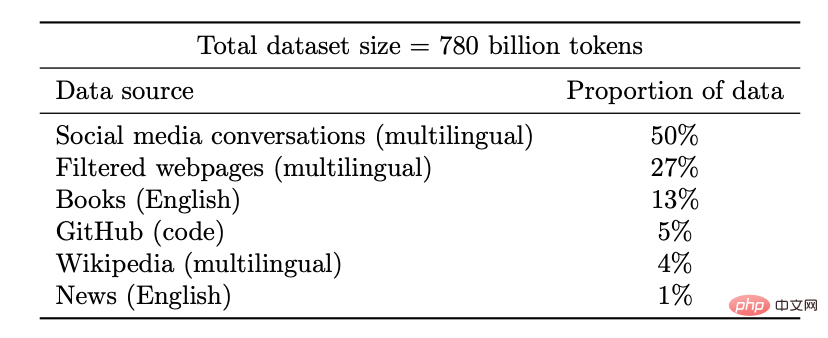
Coogle PaLM 모델의 데이터세트
새로운 기능 잠금 해제: 리소스(데이터, 컴퓨팅, 모델 크기) 투자가 증가함에 따라 딥 러닝 모델도 지속적으로 개선되고 있습니다. 이는 일부 조합 환경에서도 입증되었습니다.
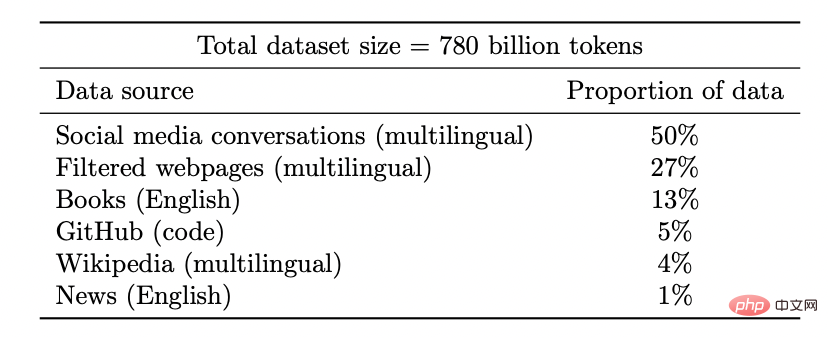
모델 크기가 증가함에 따라 PaLM은 벤치마크에서 뚜렷한 개선을 보여주고 농담이 재미있는 이유를 설명하는 것과 같은 놀라운 기능을 잠금 해제합니다.
성능은 손실이나 데이터와 거의 독립적입니다. 자체 감독 손실이 여러 개 있고, 여러 대비 및 재구성 손실이 실제로 이미지 연구에 사용되며, 언어 모델은 일방적 재구성(다음 토큰 예측)을 사용하거나 마스크 모델을 사용하여 예측이 이루어집니다. 왼쪽과 오른쪽에서 토큰의 마스크 입력입니다. 약간 다른 데이터 세트를 사용하는 것도 가능합니다. 이는 효율성에 영향을 미칠 수 있지만 "합리적인" 선택이 이루어지는 한 원래 리소스는 사용된 특정 손실이나 데이터 세트보다 예측 성능을 더 향상시키는 경우가 많습니다.
어떤 경우는 다른 경우보다 더 어렵습니다. 이 점은 자기 지도 학습에만 국한되지 않습니다. 데이터 포인트에는 고유한 "난이도 수준"이 있는 것 같습니다. 실제로, 학습 알고리즘마다 "기술 수준"이 다르며, 데이터 전문가마다 "난이도 수준"이 다릅니다(분류자가 포인트를 올바르게 분류할 확률은 기술에 따라 단조롭게 증가하고 난이도에 따라 단조롭게 감소합니다).
"기술 대 난이도" 패러다임은 Recht et al.과 Miller et al.이 발견한 "정확도" 현상에 대한 가장 명확한 설명입니다. Kaplen, Ghosh, Garg 및 Nakkiran의 논문에서는 데이터 세트의 다양한 입력이 일반적으로 다양한 모델군에 견고한 고유한 "난이도 프로필"을 갖는 방법도 보여줍니다.
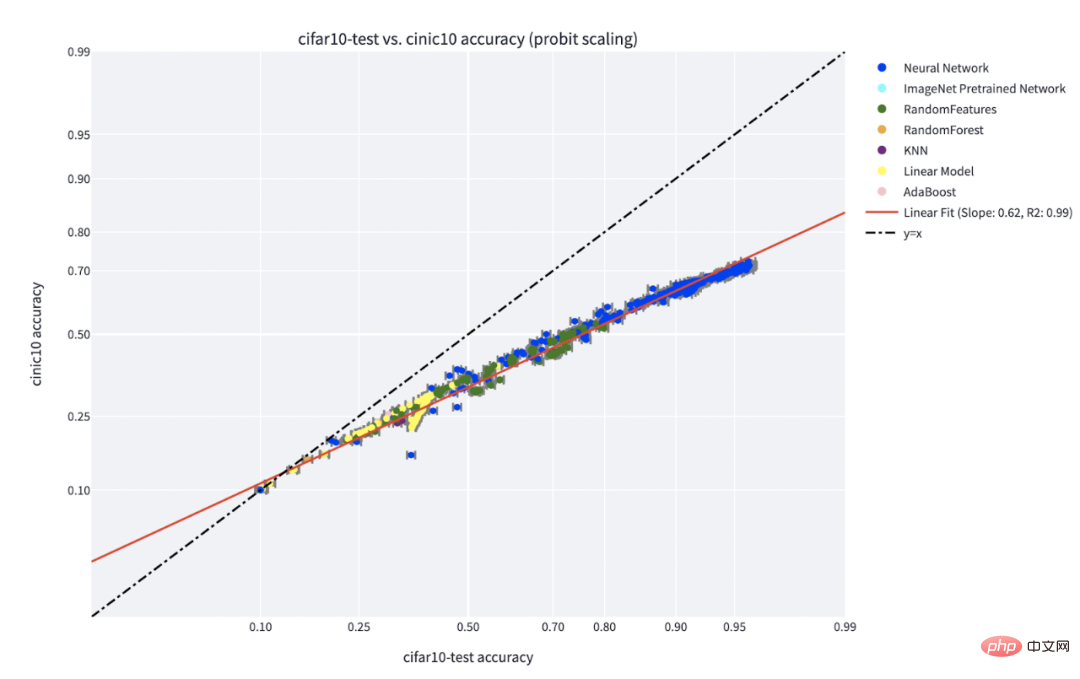
C** IFAR-10에서 훈련되고 CINIC-10에서 테스트된 분류기에 대한 라인 현상의 정확도입니다. 그림 출처: https://millerjohnp-linearfits-app-app-ryiwcq.streamlitapp.com/
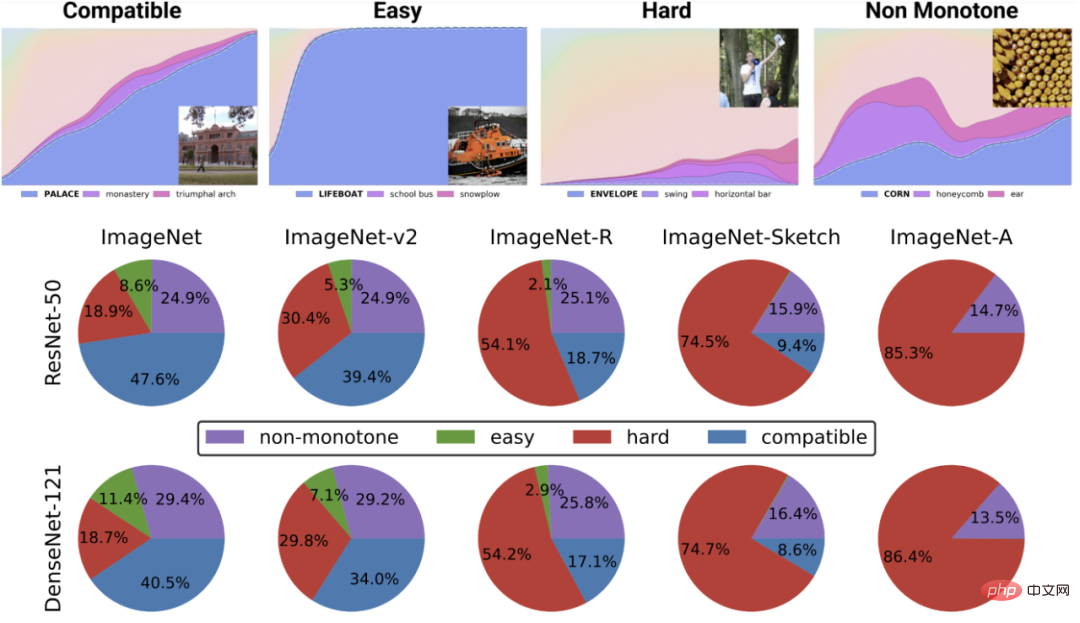
상단 그림은 분류기의 전역 정확도 함수로서 가장 가능성이 높은 클래스의 다양한 소프트맥스 확률을 보여줍니다. 특정 클래스의 경우 카테고리는 훈련 시간을 기준으로 색인화됩니다. 하단 원형 차트는 다양한 데이터 세트를 다양한 유형의 점으로 분해한 것을 보여줍니다(이 분해는 다양한 신경 구조에서 유사합니다).
교육은 교육입니다. 최신 대형 모델의 교육은 모델을 데이터에 맞추는 것보다 학생을 가르치는 것과 비슷해 보입니다. 학생들이 이해하지 못하거나 피곤함을 느끼면 "휴식"을 하거나 다른 방법을 시도합니다(교육의 차이). Meta의 대규모 모델 훈련 로그는 유익합니다. 하드웨어 문제 외에도 훈련 중에 다른 최적화 알고리즘을 전환하고 "핫 스와핑" 활성화 기능(GELU에서 RELU로)을 고려하는 등의 개입도 볼 수 있습니다. 모델 훈련을 표현을 학습하는 것이 아니라 데이터를 맞추는 것으로 생각한다면 후자가 별로 의미가 없습니다.
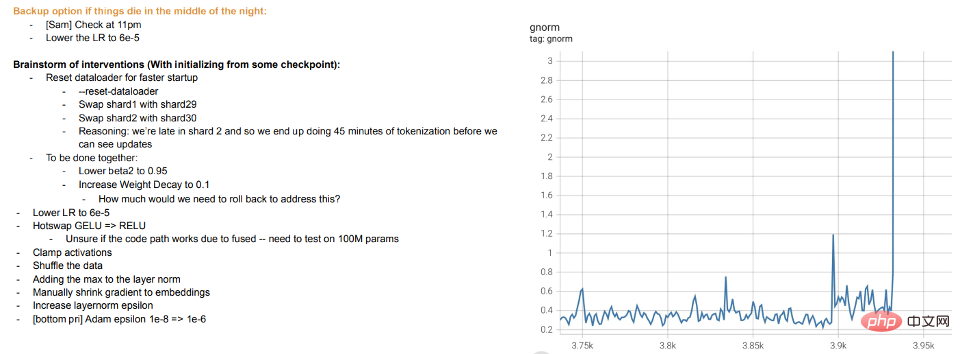
메타 훈련 로그 발췌
4.1 그런데 지도 학습은 어떻습니까?
자기 지도 학습은 앞서 논의했지만 딥 러닝의 대표적인 예는 여전히 지도 학습입니다. 결국, 딥 러닝의 "ImageNet 순간"은 ImageNet에서 나왔습니다. 그렇다면 위에서 논의한 내용이 이 설정에도 여전히 적용됩니까?
첫째, 대규모 지도 딥러닝의 출현은 고품질의 레이블이 지정된 대규모 데이터세트(예: ImageNet) 덕분에 다소 우연이었습니다. 상상력이 좋으면 딥러닝이 먼저 비지도 학습을 통해 자연어 처리 분야에서 획기적인 발전을 이루다가 비전과 지도 학습으로 넘어가는 대안의 역사를 상상할 수 있습니다.
두 번째로, 지도 학습과 자기 지도 학습은 완전히 다른 손실 함수를 사용함에도 불구하고 실제로 "내부적으로" 유사하게 동작한다는 증거가 있습니다. 둘 다 일반적으로 동일한 성능을 달성합니다. 구체적으로, 각각에 대해 자체 감독으로 훈련된 깊이 d 모델의 첫 번째 k 레이어를 성능 손실이 거의 없이 지도 모델의 마지막 d-k 레이어와 결합할 수 있습니다.
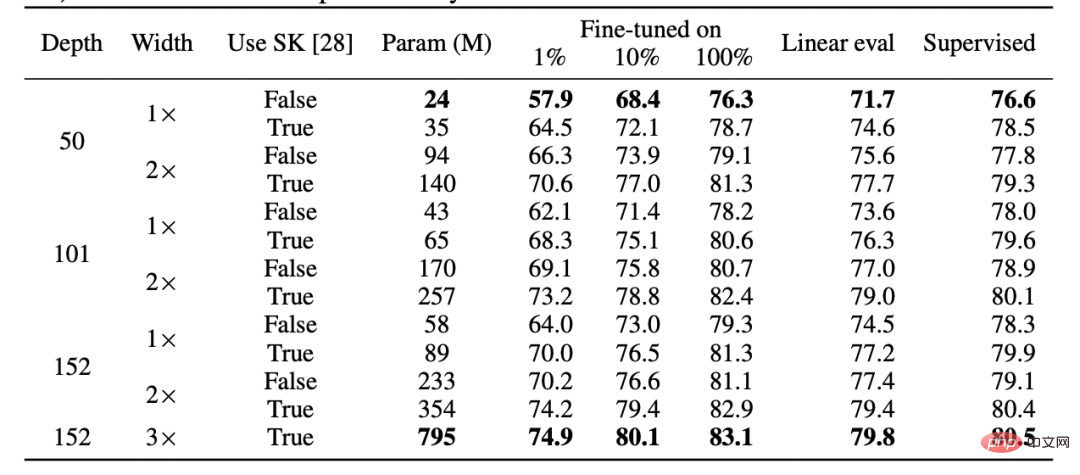
SimCLR v2 용지용 테이블. 지도 학습, 미세 조정(100%) 자체 지도 및 자체 지도 + 선형 감지 간의 성능에 대한 일반적인 유사성에 유의하세요(출처: https://arxiv.org/abs/2006.10029)
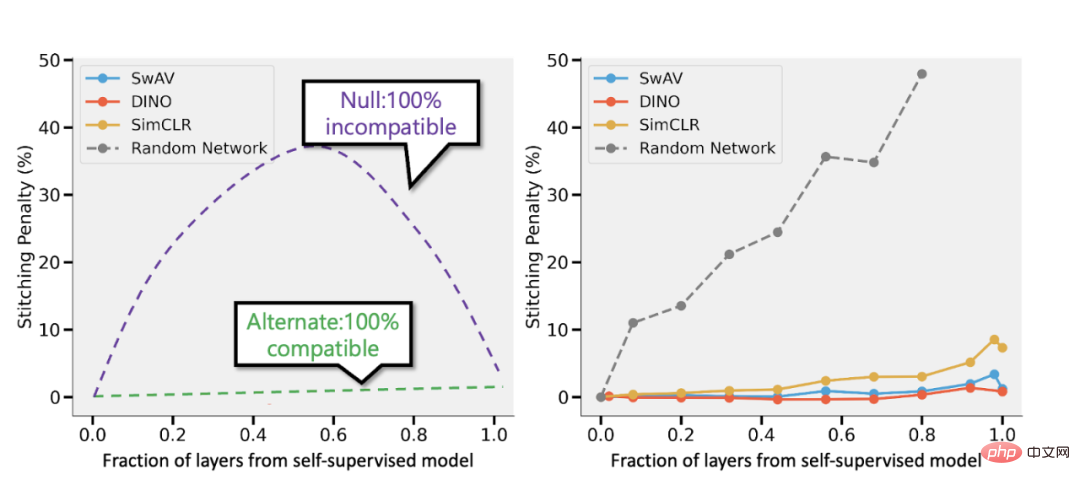
Spliced 감독 모델 및 Bansal et al.(https://arxiv.org/abs/2106.07682)의 감독 모델. 왼쪽: 자기 지도 모델의 정확도가 지도 모델보다 3% 낮다면, 완전히 호환 가능한 표현은 레이어의 p 부분이 자기 지도 모델에서 나올 때 p 3%의 스플라이싱 페널티가 발생합니다. 모델. 모델이 완전히 호환되지 않는 경우 더 많은 모델이 병합됨에 따라 정확도가 급격히 떨어질 것으로 예상됩니다. 오른쪽: 다양한 자가 감독 모델을 결합한 실제 결과.
자기 감독 + 단순 모델의 장점은 기능 학습 또는 "딥 러닝 마법"(심층 표현 기능으로 수행)과 통계적 모델 피팅(선형 또는 기타 "단순" 분류기로 수행)을 결합할 수 있다는 것입니다. 이 표현) 분리.
마지막으로, 이는 추측에 가깝지만 사실 "메타 학습"은 종종 학습 표현과 동일시되는 것 같습니다(참조: https://arxiv.org/abs/1909.09157, https://arxiv. org/abs/2206.03271) 이는 모델 최적화의 목표와 상관없이 이것이 대체로 이루어지고 있음을 보여주는 또 다른 증거라고 볼 수 있습니다.
4.2 과잉 매개변수화에 대해 어떻게 해야 하나요?
이 기사에서는 통계 학습 모델과 실제 딥 러닝의 차이점에 대한 전형적인 예로 간주되는 "편향-분산 절충"의 부족과 과도하게 매개변수화된 모델의 일반화 능력을 건너뜁니다.
왜 건너뛰나요? 두 가지 이유가 있습니다:
- 우선, 지도 학습이 실제로 자기 지도 + 단순 학습과 동일하다면 이것이 일반화 능력을 설명할 수 있습니다.
- 둘째, 과도한 매개변수화는 딥러닝 성공의 열쇠가 아닙니다. 딥 네트워크가 특별한 이유는 샘플 수에 비해 크기가 크다는 것이 아니라 절대적인 크기 때문입니다. 실제로, 일반적으로 비지도/자기 지도 학습에서는 모델이 과도하게 매개변수화되지 않습니다. 매우 큰 언어 모델의 경우에도 데이터 세트가 더 큽니다.

Nakkiran-Neyshabur-Sadghi "딥 부트스트랩" 논문은 현대 아키텍처가 "과다 매개변수화" 또는 "과소 샘플링" 체제에서 유사하게 동작함을 보여줍니다(과적합이 발생할 때까지 여러 시대에 대해 제한된 데이터에 대해 훈련된 모델: " 위 그림의 Real World'), 'under-parameterized' 또는 'online' 상태에서도 마찬가지입니다(모델은 단일 에포크에 대해 학습되었으며 각 샘플은 한 번만 표시됩니다. 위 그림의 'Ideal World'). 그림). 이미지 출처: https://arxiv.org/abs/2010.08127
Summary
통계 학습은 확실히 딥 러닝에서 중요한 역할을 합니다. 그러나 유사한 용어와 코드를 사용함에도 불구하고 딥러닝을 단순히 기존 모델보다 더 많은 매개변수를 사용하여 모델을 맞추는 것으로 보는 것은 성공에 중요한 많은 부분을 무시하는 것입니다. 학생들에게 수학을 가르치는 비유도 완벽하지 않습니다.
생물학적 진화와 마찬가지로 딥 러닝에는 재사용된 규칙(예: 경험 손실이 있는 경사하강법)이 많이 포함되어 있지만 매우 복잡한 결과를 생성할 수 있습니다. 서로 다른 시기에 네트워크의 서로 다른 구성 요소는 표현 학습, 예측 피팅, 암시적 정규화 및 순수 노이즈를 포함하여 서로 다른 내용을 학습하는 것으로 보입니다. 연구자들은 딥러닝에 대한 질문에 답하는 것은 물론이고 질문할 수 있는 올바른 렌즈를 여전히 찾고 있습니다.
위 내용은 학습 = 피팅? 딥러닝과 고전적인 통계는 같은 것인가요?의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!

