Python을 사용하여 상위 10개 고전 정렬 알고리즘 구현
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWB앞으로
- 2023-04-16 08:55:022044검색

10가지 고전적인 정렬 알고리즘에는 버블 정렬, 선택 정렬, 퀵 정렬, 병합 정렬, 힙 정렬, 삽입 정렬, 힐 정렬, 카운팅 정렬, 버킷 정렬, 기수 정렬 등이 포함됩니다.
물론, 다른 정렬 알고리즘도 있으므로 계속 연구할 수 있습니다.
01 Bubble Sort
Bubble Sort는 정렬할 요소를 반복적으로 방문하여 인접한 두 요소를 차례로 비교하고 순서가 잘못된 경우 제거하는 비교적 간단한 정렬 알고리즘입니다. 교체해야 할 요소가 더 많아지고 정렬이 완료됩니다.
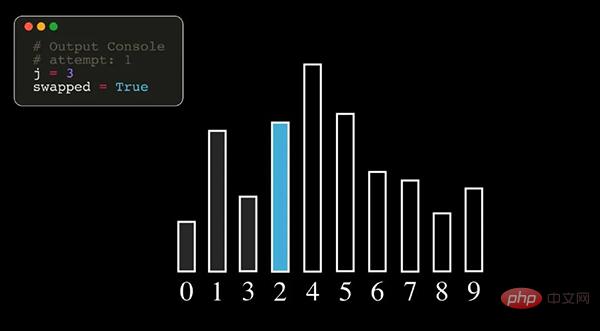
참고: 위 그림에서 숫자는 데이터 시퀀스의 원래 인덱스 번호를 나타냅니다.
알고리즘 프로세스
- 인접한 요소를 비교합니다. 전자가 후자보다 크면 위치를 바꿉니다.
- 모든 것이 완료될 때까지 정렬된 배열의 인접한 요소의 각 쌍에 대해 동일한 작업을 수행합니다. 이때 마지막 요소는 이 정렬 라운드에서 가장 큰 숫자가 됩니다.
- 비교할 필요가 없는 요소가 없을 때까지 나머지 요소에 대해 위 단계를 계속 반복합니다.
버블 정렬은 매번 가장 큰 요소를 찾기 때문에 n-1번 순회해야 합니다(n은 데이터 시퀀스의 길이).
알고리즘 특징
가장 빠른 시기(Best Cases): 입력 데이터가 이미 양수 순서인 경우.
최악의 경우: 입력 데이터의 순서가 반대인 경우.
파이썬 코드
def bubble_sort(lst): n = len(lst) for i in range(n): for j in range(1, n - i): if lst[j - 1] > lst[j]: lst[j - 1], lst[j] = lst[j], lst[j - 1] return lst
02 선택 정렬
선택 정렬의 원리
선택 정렬의 원리는 매 라운드마다 정렬할 레코드 중에서 가장 작은 요소를 선택하여 시퀀스의 시작 위치에 저장하고, 그런 다음 정렬되지 않은 나머지 요소 중에서 가장 작은 요소를 찾아서 정렬된 시퀀스의 끝에 넣습니다. 정렬할 모든 데이터 요소의 수가 0이 될 때까지 계속됩니다. 작은 값에서 큰 값으로 정렬된 데이터 시퀀스를 가져옵니다.
각 라운드에서 가장 큰 값을 갖는 요소를 찾을 수도 있습니다. 이 경우 정렬된 배열은 결국 큰 것부터 작은 것 순으로 정렬됩니다.
선택 정렬은 매번 가장 작은(가장 큰) 요소를 선택하므로 n-1번 순회해야 합니다.
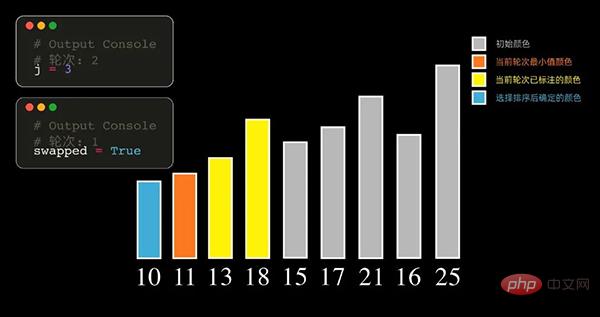
파이썬 코드
def selection_sort(lst): for i in range(len(lst) - 1): min_index = i for j in range(i + 1, len(lst)): if lst[j] < lst[min_index]: min_index = j lst[i], lst[min_index] = lst[min_index], lst[i] return lst
03 Quick Sort
퀵 정렬(Quick Sort)은 1960년대 미국 토니 홀이 제안한 정렬 방법입니다. 이 정렬 방법은 당시에는 이미 매우 빠른 정렬 방법이었습니다. 그래서 이름을 따서 "퀵 정렬(quick sort)"이라고 부릅니다.
알고리즘 프로세스
- 먼저 데이터 시퀀스에서 숫자를 기준 숫자로 선택합니다(기준, 첫 번째 숫자를 사용하는 것이 일반적입니다).
- 파티셔닝 과정에서 기본 숫자보다 작은 모든 숫자는 왼쪽에 배치되고 그보다 크거나 같은 모든 숫자는 오른쪽에 배치됩니다.
- 각 간격에 하나의 숫자만 남을 때까지 왼쪽 및 오른쪽 간격에 대해 두 번째 단계를 재귀적으로 반복합니다.
데이터 시퀀스 간의 순서가 고정되어 있기 때문입니다. 마지막으로 이러한 하위 시퀀스를 한 번에 결합하여 전체 정렬이 완료됩니다.
아래와 같이 데이터 시퀀스의 경우 먼저 첫 번째 데이터 15를 기본 숫자로 취하고 15보다 작은 숫자를 왼쪽에 배치하고 15보다 큰 숫자(크거나 같음)를 오른쪽에 배치합니다
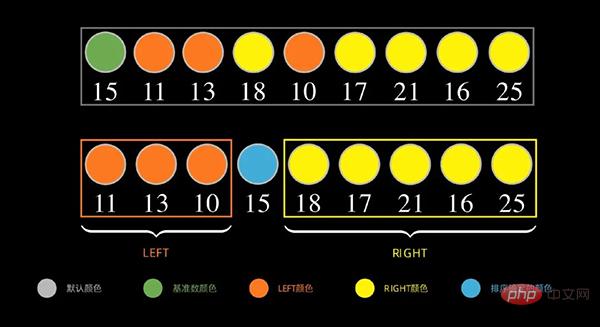
다음, 왼쪽 부분에 대해서도 위의 단계를 아래 그림과 같이 반복하고, 왼쪽 순서의 첫 번째 데이터 11을 밑수로 취하고, 11보다 작은 숫자를 왼쪽에 넣은 다음, 오른쪽의 숫자는 11보다 크거나 같습니다.
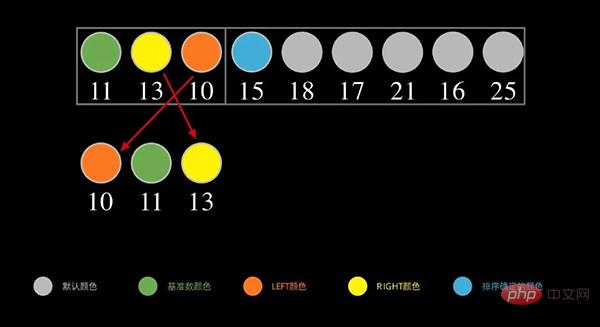
각 간격에 하나의 숫자만 남을 때까지 위 프로세스를 계속해서 재귀적으로 반복합니다. 이것으로 정렬이 완료됩니다
파이썬 코드
def quick_sort(lst): n = len(lst) if n <= 1: return lst baseline = lst[0] left = [lst[i] for i in range(1, len(lst)) if lst[i] < baseline] right = [lst[i] for i in range(1, len(lst)) if lst[i] >= baseline] return quick_sort(left) + [baseline] + quick_sort(right)
04 병합 정렬
알고리즘 아이디어
병합 정렬은 병합 작업을 기반으로 하는 효과적인 정렬 알고리즘입니다. 이 알고리즘은 분할 정복 방법의 매우 일반적인 응용 프로그램입니다. 병합 정렬은 이미 정렬된 두 개의 하위 시퀀스를 정렬된 시퀀스로 병합합니다.
알고리즘 흐름
주요 두 단계(분할, 병합)
- 1단계: 요소가 하나만 남을 때까지 시퀀스를 분할합니다.
- 2단계: 분할이 완료된 후 재귀 병합을 시작합니다.
아이디어: 정렬되지 않은 시퀀스가 있다고 가정하고 먼저 분할 방법을 사용하여 시퀀스를 정렬된 하위 시퀀스로 나눕니다(한 요소가 남을 때까지). 그런 다음 병합 메서드를 사용하여 정렬된 하위 시퀀스를 정렬된 시퀀스로 병합합니다.
Graphic Algorithm
Split
데이터 시퀀스 [15,11,13,18,10]의 경우 데이터 시퀀스의 중간 위치부터 먼저 분할을 시작하고 중간 위치는
으로 설정됩니다. 첫 번째 분할 다음과 같습니다:
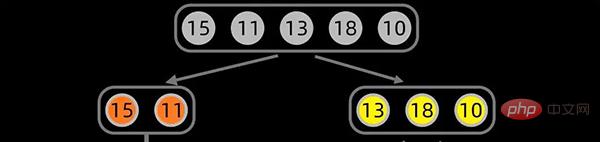
第一次拆分后,依次对子序列进行拆分,拆分过程如下:
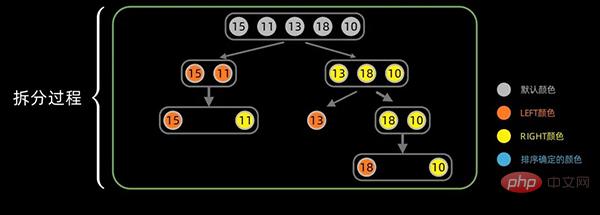
合并
合并过程中,对于左右分区以及其子区间,递归使用合并方法。先从左边最小的子区间开始,对于每个区间,依次将最小的数据放在最左边,然后对右边区间也执行同样的操作。
合并过程的完整图示如下:
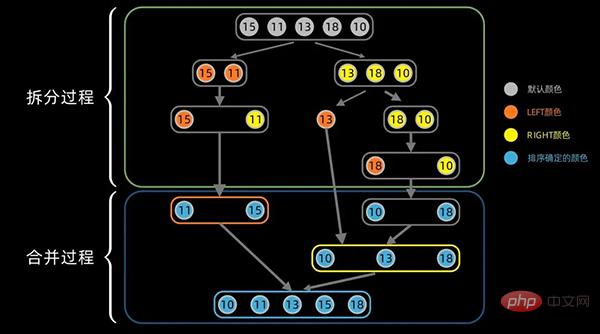
Python代码
def merge_sort(lst): def merge(left,right): i = 0 j = 0 result = [] while i < len(left) and j < len(right): if left[i] <= right[j]: result.append(left[i]) i += 1 else: result.append(right[j]) j += 1 result = result + left[i:] + right[j:] return result n = len(lst) if n <= 1: return lst mid = n // 2 left = merge_sort(lst[:mid]) right = merge_sort(lst[mid:]) return merge(left,right)
05堆排序
要理解堆排序(Heap Sort)算法,首先要知道什么是“堆”。
堆的定义
对于 n 个元素的数据序列
,当且仅当满足下列情形之一时,才称之为 堆:
情形1:
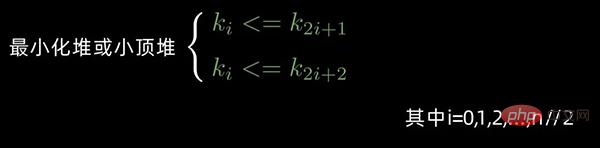
情形2:
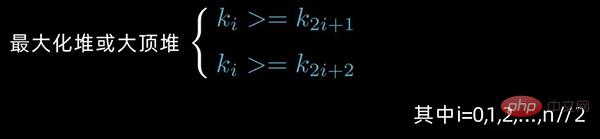
若序列
是堆,则堆顶元素必为序列中n个元素的最小值或最大值。
小顶堆如下图所示:
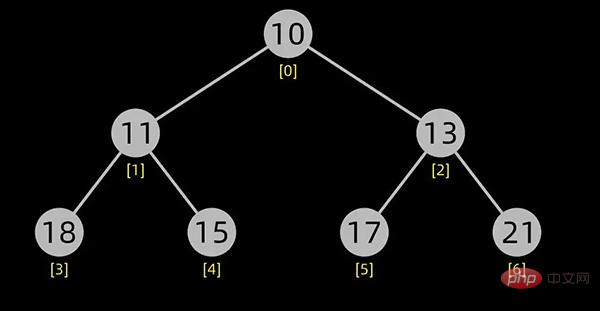
小顶堆
大顶堆如下图所示:
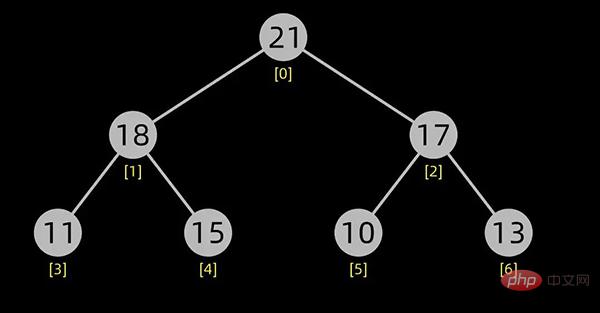
大顶堆
若在输出堆顶的最小值(或最大值)之后,使得剩余n-1个元素的序列重又建成一个堆,则得到n个元素的次小值(或次大值)。如此反复执行,便能得到一个有序序列,这个过程称之为 堆排序。
堆的存储
一般用数组来表示堆,若根结点存在序号 0 处, i 结点的父结点下标就为 (i-1)/2。i 结点的左右子结点下标分别为 2*i+1和 2*i+2 。
对于上面提到的小顶堆和大顶堆,其数据存储情况如下:
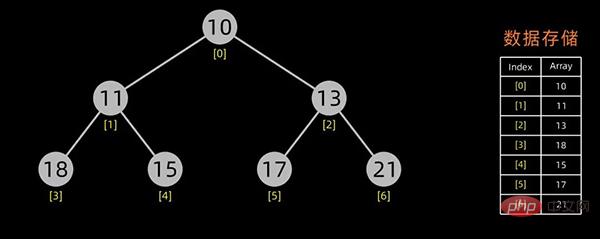
小顶堆
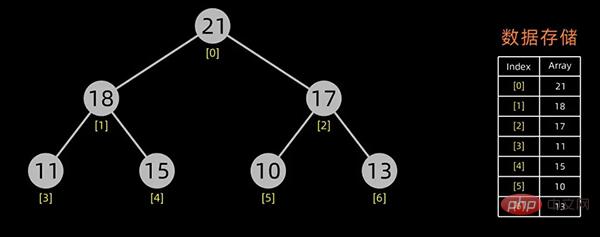
大顶堆
每幅图的右边为其数据存储结构,左边为其逻辑结构。
堆排序
实现堆排序需要解决两个问题:
- 如何由一个无序序列建成一个堆?
- 如何在输出堆顶元素之后,调整剩余元素成为一个新的堆?
堆的初始化
第一个问题实际上就是堆的初始化,下面来阐述下如何构造初始堆,假设初始的数据序列如下:

咱们首先需要将其以树形结构来展示,如下:
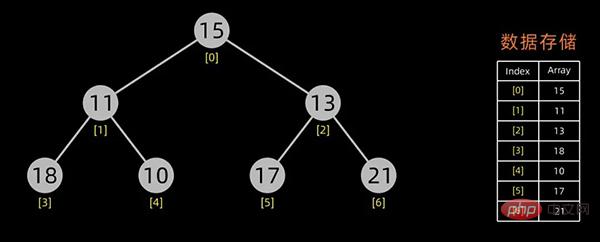
初始化堆的时候是对所有的非叶子结点进行筛选。
最后一个非终端元素的下标是 [n/2] 向下取整,所以筛选只需要从第 [n/2] 向下取整个元素开始,从后往前进行调整。
从最后一个非叶子结点开始,每次都是从父结点、左边子节点、右边子节点中进行比较交换,交换可能会引起子结点不满足堆的性质,所以每次交换之后需要重新对被交换的子结点进行调整。
以小顶堆为例,构造初始堆的过程如下:
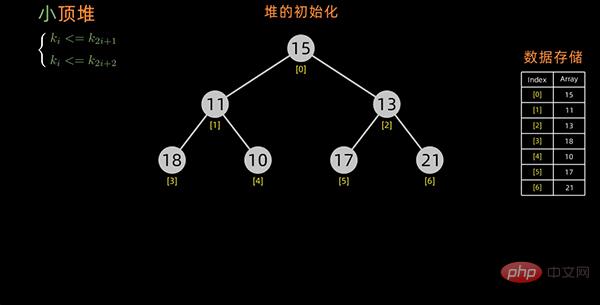
进行堆排序
有了初始堆之后就可以进行排序了。
堆排序是一种选择排序。建立的初始堆为初始的无序区。
排序开始,首先输出堆顶元素(因为它是最值),将堆顶元素和最后一个元素交换,这样,第n个位置(即最后一个位置)作为有序区,前n-1个位置仍是无序区,对无序区进行调整,得到堆之后,再交换堆顶和最后一个元素,这样有序区长度变为2。。。
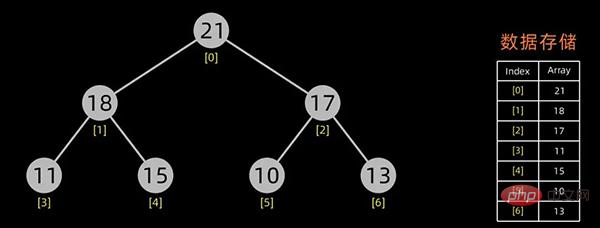
大顶堆
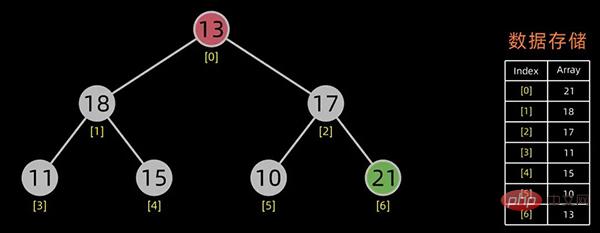
交换堆顶元素和最后的元素
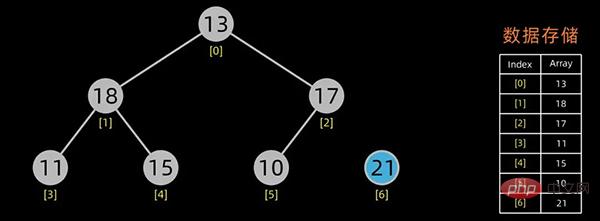
无序区-1,有序区+1
不断进行此操作,将剩下的元素重新调整为堆,然后输出堆顶元素到有序区。每次交换都导致无序区-1,有序区+1。不断重复此过程直到有序区长度增长为n-1,排序完成。
Python代码
def heap_sort(lst): def adjust_heap(lst, i, size): left_index = 2 * i + 1 right_index = 2 * i + 2 largest_index = i if left_index < size and lst[left_index] > lst[largest_index]: largest_index = left_index if right_index < size and lst[right_index] > lst[largest_index]: largest_index = right_index if largest_index != i: lst[largest_index], lst[i] = lst[i], lst[largest_index] adjust_heap(lst, largest_index, size) def built_heap(lst, size): for i in range(len(lst)//2)[::-1]: adjust_heap(lst, i, size) size = len(lst) built_heap(lst, size) for i in range(len(lst))[::-1]: lst[0], lst[i] = lst[i], lst[0] adjust_heap(lst, 0, i) return lst
06插入排序
插入排序(Insertion Sort)就是每一步都将一个需要排序的数据按其大小插入到已经排序的数据序列中的适当位置,直到全部插入完毕。
插入排序如同打扑克牌一样,每次将后面的牌插到前面已经排好序的牌中。

Python代码
def insertion_sort(lst): for i in range(len(lst) - 1): cur_num, pre_index = lst[i+1], i while pre_index >= 0 and cur_num < lst[pre_index]: lst[pre_index + 1] = lst[pre_index] pre_index -= 1 lst[pre_index + 1] = cur_num return lst
07希尔排序
基本原理
希尔排序(Shell Sort)是插入排序的一种更高效率的实现。
希尔排序的核心在于间隔序列的设定。既可以提前设定好间隔序列,也可以动态的定义间隔序列。
这里以动态间隔序列为例来描述。初始间隔(gap值)为数据序列长度除以2取整,后续间隔以 前一个间隔数值除以2取整为循环,直到最后一个间隔值为 1 。
对于下面这个数据序列,初始间隔数值为5
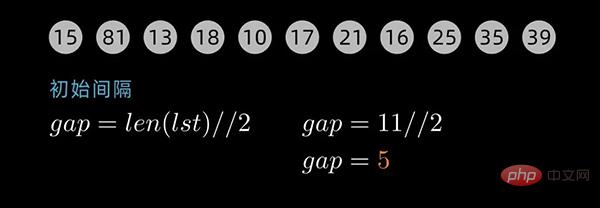
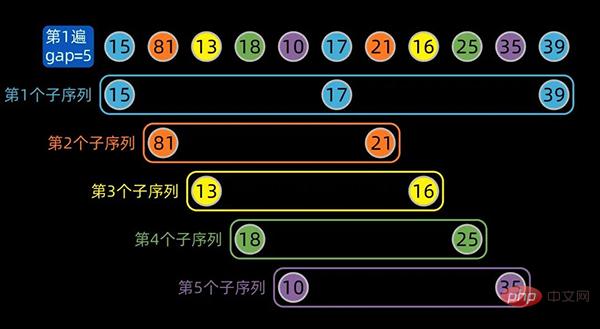
先将数据序列按间隔进行子序列分组,第一个子序列的索引为[0,5,10],这里分成了5组。

为方便大家区分不同的子序列,对同一个子序列标注相同的颜色,分组情况如下:
分组结束后,子序列内部进行插入排序,gap为5的子序列内部排序后如下:
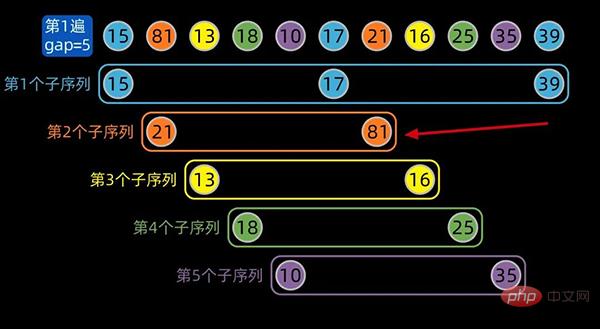

注:红色箭头标注的地方,是子序列内部排序后的状态
接下来选取第二个间隔值,按照间隔值进行子序列分组,同样地,子序列内部分别进行插入排序;
如果数据序列比较长,则会选取第3个、第4个或者更多个间隔值,重复上述的步骤。
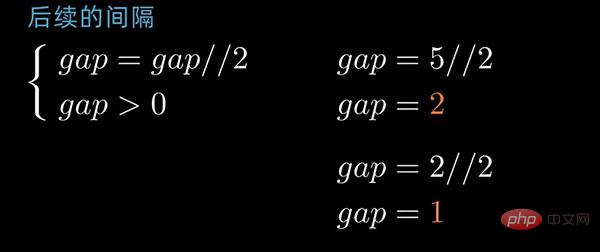
gap为2的排序情况前后对照如下:

最后一个间隔值为1,这一次相当于简单的插入排序。但是经过前几次排序,序列已经基本有序,因此最后一次排序时间效率就提高了很多。

Python代码
def shell_sort(lst): n = len(lst) gap = n // 2 while gap > 0: for i in range(gap, n): for j in range(i, gap - 1, -gap): if lst[j] < lst[j - gap]: lst[j], lst[j - gap] = lst[j - gap], lst[j] else: break gap //= 2 return lst
08计数排序
基本原理
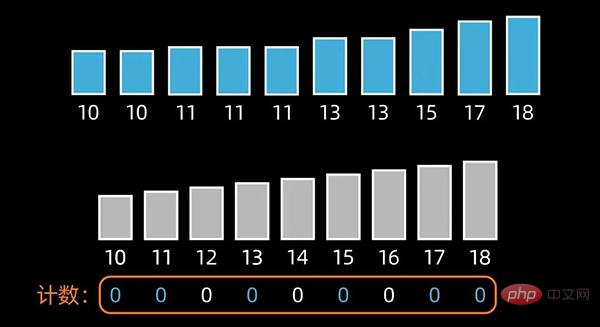
计数排序(Counting Sort)的核心在于将输入的数据值转化为键,存储在额外开辟的数组空间中。计数排序要求输入的数据必须是有确定范围的整数。
算法的步骤如下:
先找出待排序的数组中最大和最小的元素,新开辟一个长度为 最大值-最小值+1 的数组;
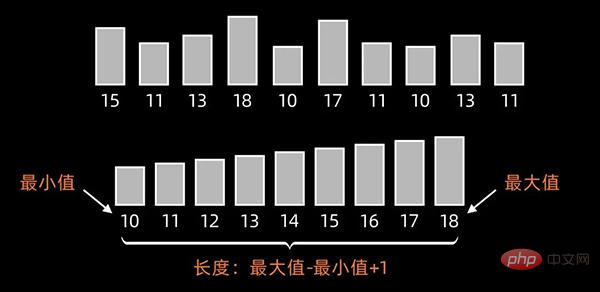
然后,统计原数组中每个元素出现的次数,存入到新开辟的数组中;
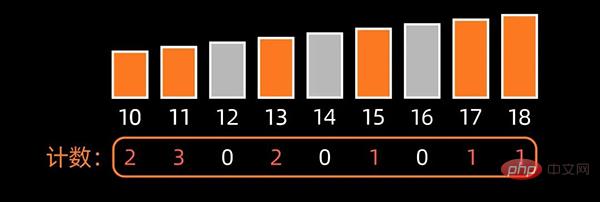
接下来,根据每个元素出现的次数,按照新开辟数组中从小到大的秩序,依次填充到原来待排序的数组中,完成排序。
Python代码
def counting_sort(lst): nums_min = min(lst) bucket = [0] * (max(lst) + 1 - nums_min) for num in lst: bucket[num - nums_min] += 1 i = 0 for j in range(len(bucket)): while bucket[j] > 0: lst[i] = j + nums_min bucket[j] -= 1 i += 1 return lst
09桶排序
基本思想
简单来说,桶排序(Bucket Sort)就是把数据分组,放在一个个的桶中,对每个桶里面的数据进行排序,然后将桶进行数据合并,完成桶排序。
该算法分为四步,包括划分桶、数据入桶、桶内排序、数据合并。
桶的划分过程
这里详细介绍下桶的划分过程。
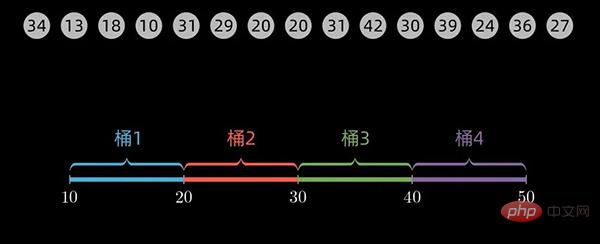
对于一个数值范围在10到 49范围内的数组,我们取桶的大小为10 (defaultBucketSize = 10),则第一个桶的范围为 10到20,第二个桶的数据范围是20到30,依次类推。最后,我们一共需要4个桶来放入数据。

排序过程
对于下面这个数据序列,初始设定桶的大小为 20 (defaultBucketSize = 20),经计算,一共需要4个桶来放入数据。
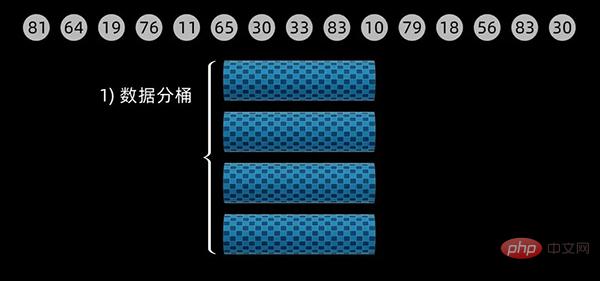
然后将原始数组按数值大小放入到对应的桶中,完成数据分组。
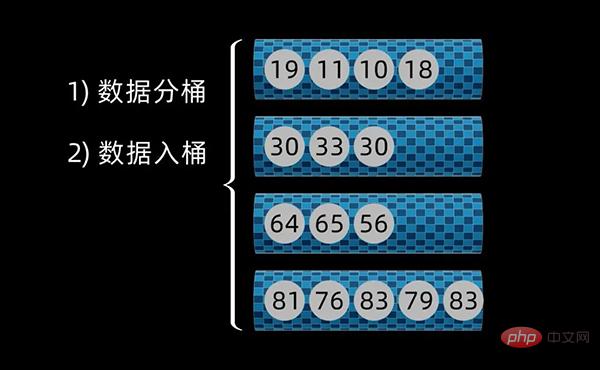
对于桶内的数据序列,这时可以用冒泡排序、选择排序等多种排序算法来对数据进行排序。这些算法,在之前的视频里已有介绍,大家可以去了解下。
这里,我选用 冒泡排序 来对桶内数据进行排序。
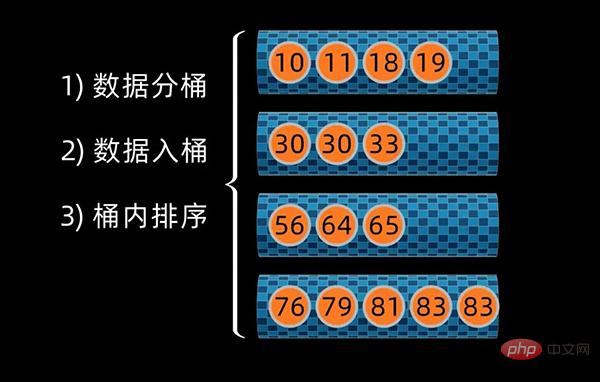
桶内排序完成后,将数据按桶的顺序进行合并,这样就得到所有数值排好序的数据序列了

Python代码
def bucket_sort(lst, defaultBucketSize=4): maxVal, minVal = max(lst), min(lst) bucketSize = defaultBucketSize bucketCount = (maxVal - minVal) // bucketSize + 1 buckets = [[] for i in range(bucketCount)] for num in lst: buckets[(num - minVal) // bucketSize].append(num) lst.clear() for bucket in buckets: bubble_sort(bucket) lst.extend(bucket) return lst
10基数排序
基数排序(radix sort)属于“分配式排序”(distribution sort),它是透过键值的部份信息,将要排序的元素分配至某些“桶”中,以达到排序的作用。
基数排序适用于所有元素均为正整数的数组。
基本思想
排序过程分为“分配”和“收集”。
排序过程中,将元素分层为多个关键码进行排序(一般按照数值的个位、十位、百位、…… 进行区分),多关键码排序按照从最主位关键码到最次位关键码或从最次位到最主位关键码的顺序逐次排序。
基数排序的方式可以采用最低位优先LSD(Least sgnificant digital)法或最高位优先MSD(Most sgnificant digital)法,LSD的排序方式由键值的最右边开始,而MSD则相反,由键值的最左边开始。
LSD的基数排序适用于位数小的数列,如果位数多的话,使用MSD的效率会比较好,MSD的方式恰与LSD相反,是由高位数为基底开始进行分配,其他的演算方式则都相同。
算法流程
这里以最低位优先LSD为例。
先根据个位数的数值,在扫描数值时将它们分配至编号0到9的桶中,然后将桶子中的数值串接起来。
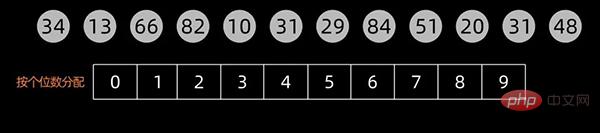
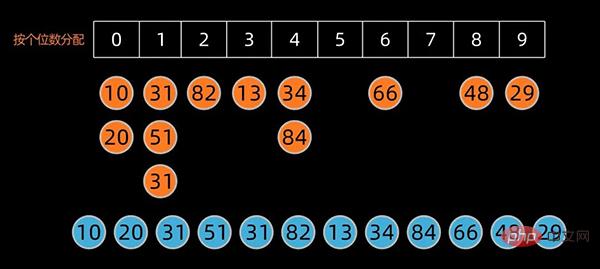
将这些桶子中的数值重新串接起来,成为新的序列,接着再进行一次分配,这次是根据十位数来分配。

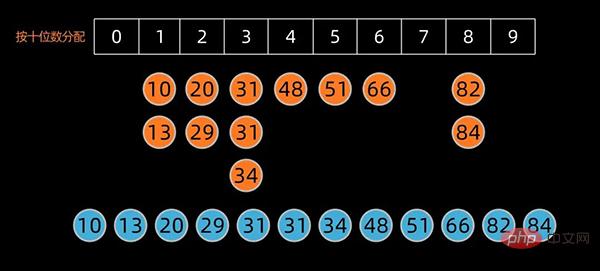
如果排序的对象有三位数以上,则持续进行以上的动作直至最高位数为止。
Python代码
# LSD Radix Sort def radix_sort(lst): mod = 10 div = 1 mostBit = len(str(max(lst))) buckets = [[] for row in range(mod)] while mostBit: for num in lst: buckets[num // div % mod].append(num) i = 0 for bucket in buckets: while bucket: lst[i] = bucket.pop(0) i += 1 div *= 10 mostBit -= 1 return lst
11小结
以上就是用 Python 来实现10种经典排序算法的相关内容。
对于这些排序算法的实现,代码其实并不是最主要的,重要的是需要去理解各种算法的基本思想、基本原理以及其内部的实现过程。
对于每种算法,用其他编程语言同样是可以去实现的。
并且,对于同一种算法,即使只用 Python 语言,也有多种不同的代码方式可以来实现,但其基本原理是一致的。
위 내용은 Python을 사용하여 상위 10개 고전 정렬 알고리즘 구현의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!

