카드 하나로 AI 페인팅 모델을 실행할 수 있습니다. 초보자도 이해할 수 있는 튜토리얼이 100만 장의 카드로 제공됩니다.

최근 AI드로잉이 인기를 끌고 있다는 사실은 다들 잘 아실 거라 믿습니다.

AI 드로잉 소프트웨어로 탄생한 작품부터 수많은 인간 아티스트를 물리치고 디지털 아트 챔피언십 우승까지, 지금까지 DALL.E, Imagen, novelai 등 국내외 플랫폼이 번성했습니다.

아마도 관련 사이트를 클릭해서 AI가 마음 속 풍경을 묘사하도록 해보거나, 자신의 잘생기고 아름다운 사진을 업로드한 후 마침내 생성된 거친 남자를 보고 웃고 웃었을 것입니다.

그럼 AI 그림의 매력을 느끼면서 혹시 생각해보신 적 있으신가요?(아니요, 분명 그랬을 겁니다), 그 뒤에 숨은 미스터리는 무엇인가요?

Δ콜로라도 테크놀로지 엑스포 디지털 아트 부문 수상작 - "스페이스 오페라"

모든 것은 DDPM이라는 모델에서 시작됩니다...

DDPM이란?

DDPM 모델, 정식 명칭은 Denoising Diffusion Probabilistic Model이며, 현재 확산 모델의 시조라고 할 수 있습니다.

GAN, VAE, Flow 등의 이전 모델과 달리 확산 모델의 전반적인 아이디어는 최적화 지향 접근 방식을 통해 순수한 노이즈 이미지에서 점진적으로 이미지를 생성하는 것입니다.

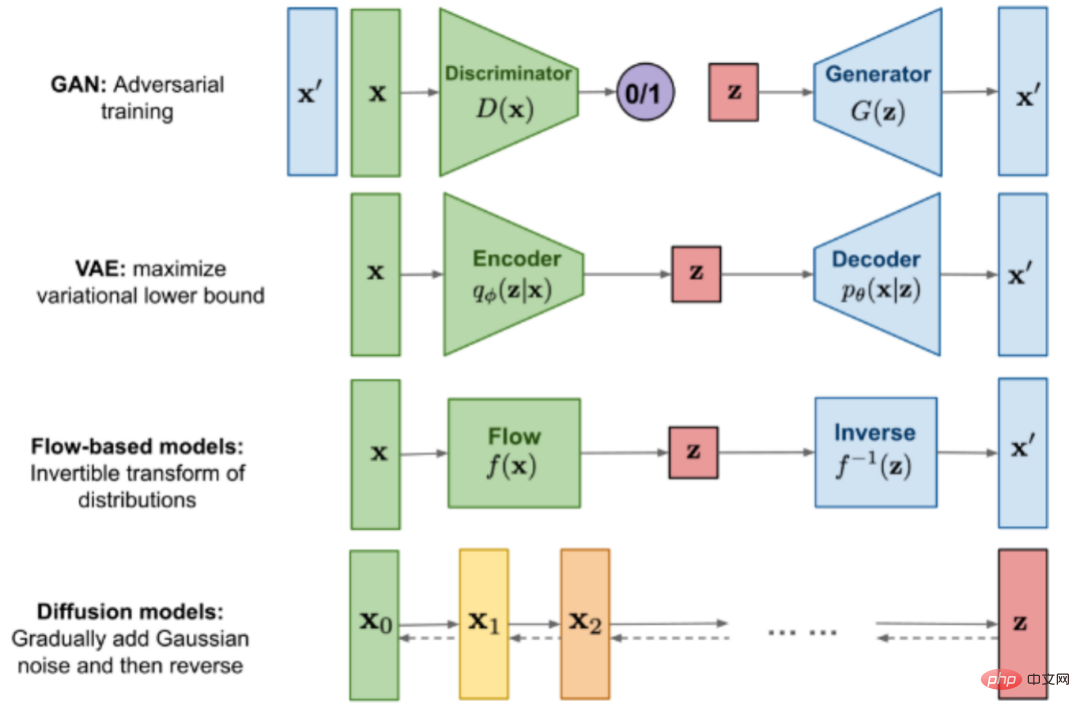
Δ이제 생성된 이미지 모델을 비교할 수 있습니다

어떤 친구들은 순수 노이즈 이미지가 무엇인지 묻습니다.

아주 간단합니다. 오래된 TV에 신호가 없을 때 '딱딱'하는 소음과 함께 나타나는 눈송이 사진은 순수한 노이즈 사진입니다.

세대 단계에서 DDPM이 하는 일은 선명한 이미지가 실제 모습을 드러낼 때까지 이러한 "눈송이"를 조금씩 제거하는 것입니다. 우리는 이 단계를 "노이즈 제거"라고 부릅니다.

Δ순수한 노이즈 사진: 오래된 TV의 눈꽃 화면

설명을 보면 노이즈 제거 작업이 실제로 꽤 복잡한 과정임을 느낄 수 있습니다.

노이즈 제거에는 정해진 규칙이 없습니다. 오랫동안 바빴지만 결국에는 이상한 사진 앞에서 울고 싶을 수도 있습니다.

물론, 사진마다 노이즈 제거 규칙도 다릅니다. 기계가 이 규칙을 학습하도록 하는 방법에 대해 누군가 훌륭한 방법을 고안했습니다.

노이즈 제거 규칙은 배우기 어렵기 때문에, 먼저 노이즈를 추가하여 사진을 순수한 노이즈 이미지로 만든 다음 전체 프로세스를 반대로 수행하면 어떨까요?

이것은 확산 모델의 전체 훈련-추론 프로세스를 설정합니다. 먼저 순방향 프로세스(순방향 프로세스)에서 이미지는 점진적으로 노이즈를 추가하여 대략적인 가우스 분포를 갖는 순수한 노이즈 이미지로 변환됩니다. 역방향 프로세스 역방향 프로세스에서 단계적으로 노이즈 제거 및 이미지 생성

마지막으로 원본 이미지와 생성된 이미지 간의 유사성을 높이는 것을 목표로 이상적인 효과가 달성될 때까지 모델이 최적화됩니다. ​

ΔDDPM 학습-추론 과정

이쯤 되면 다들 어떻게 받아들이실지 궁금하네요. 문제가 없고 쉽다고 생각되면 준비하세요. 궁극기(심층 이론)를 사용하여 시작하겠습니다.

1.1.1 순방향 프로세스

순방향 프로세스는 확산 프로세스라고도 하며 전체가 매개변수화된 마르코프 체인입니다. 초기 데이터 분포 x0~q(x)부터 시작하여 T번 동안 각 단계에서 데이터 분포에 Gaussian 노이즈가 추가됩니다. t-1 xt-1 단계에서 t xt 단계까지의 과정은 가우스 분포로 다음과 같이 표현될 수 있습니다.

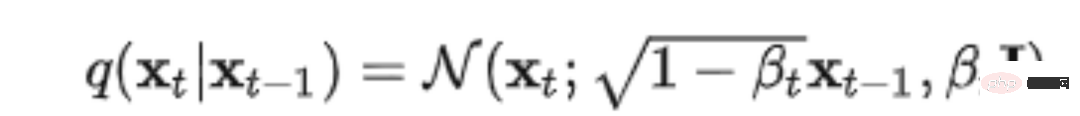적절한 설정을 사용하면 t가 계속 증가함에 따라 원래 데이터 x0은 점차 그 특성을 잃게 됩니다. 우리는 무한한 수의 노이즈 추가 단계 후에 최종 데이터 xT가 어떤 특징도 없고 완전히 무작위적인 노이즈도 없는 그림이 될 것이라는 것을 이해할 수 있습니다. 이것이 바로 우리가 처음에 "눈송이 화면"이라고 불렀던 것입니다.

이 과정에서 하이퍼파라미터 βt를 설정하여 각 단계의 변화를 제어할 수 있습니다. 초기 이미지가 무엇인지 안다는 전제하에 순방향 노이즈 추가의 전체 과정을 알고 제어할 수 있다고 할 수 있습니다. 각 단계에서 생성된 데이터가 어떤 모습인지 완벽하게 알 수 있습니다.

하지만 문제는 모든 계산을 시작점에서 시작하여 각 단계의 과정을 종합하고 천천히 원하는 특정 단계 데이터 xt로 도출해야 한다는 점입니다. 이는 너무 번거롭습니다. 다행히도 가우스 분포의 일부 특성으로 인해 한 단계로 x0에서 직접 xt를 얻을 수 있습니다. ​

주의하세요.

여기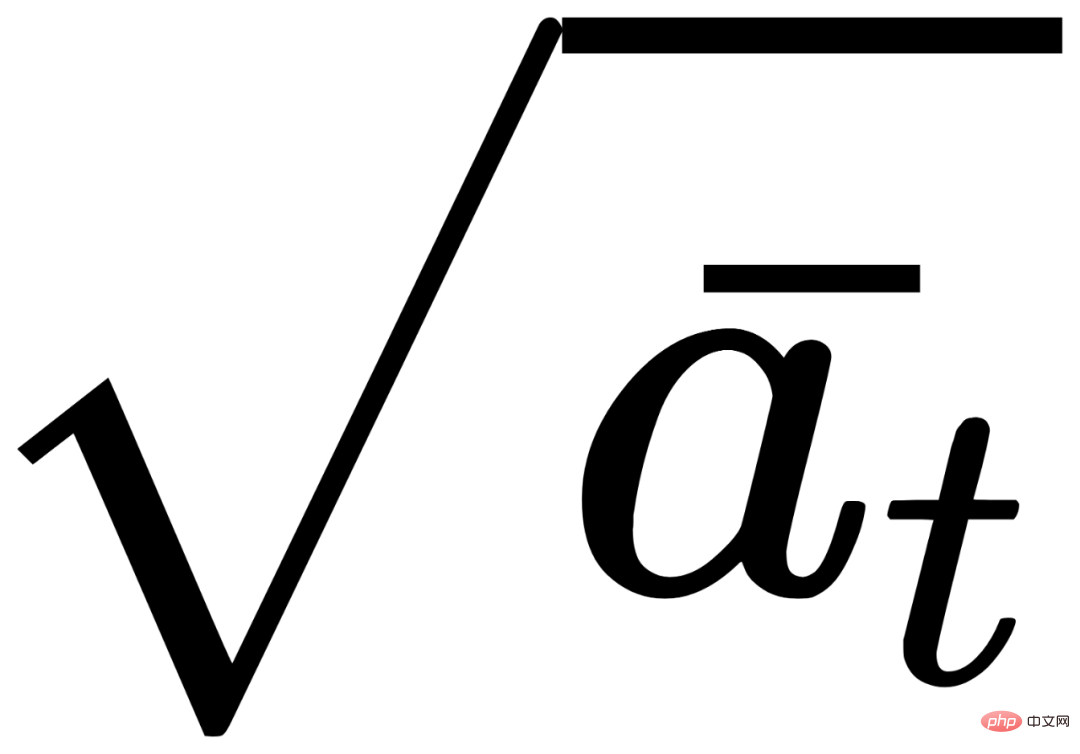

및 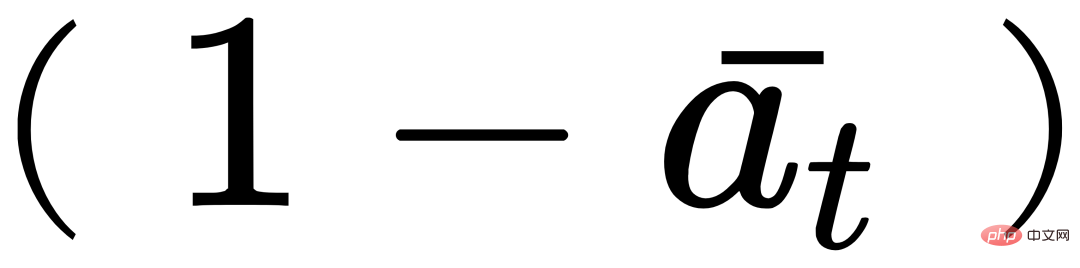은 기본적으로 하이퍼파라미터의 βt 표현인 조합 계수입니다.

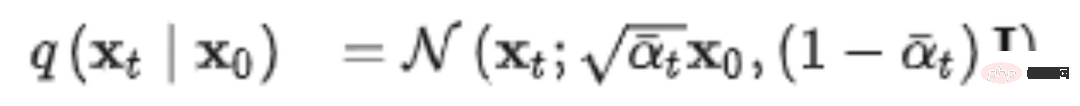
1.1.2 역과정(reverse process)

역과정도 마코프체인과 동일하지만, 여기서 사용하는 매개변수가 다릅니다. ? 이것이 바로 기계가 학습해야 하는 것입니다.

기계가 학습하는 방식을 이해하기 전에 먼저 특정 원본 데이터 x0을 기반으로 t xt 단계에서 t-1 xt-1 단계로 정확하게 추론하는 과정은 무엇인지 생각해 보세요.

답은 이것이 여전히 가우스 분포로 표현될 수 있다는 것입니다.

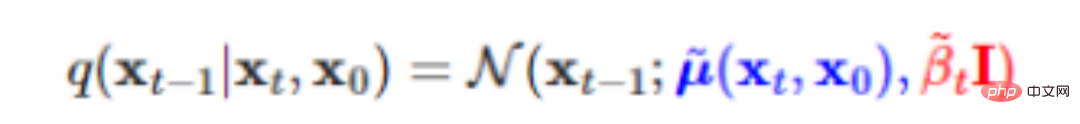
여기서는 x0을 고려해야 하며, 이는 역과정으로 생성된 최종 이미지가 여전히 원본 데이터와 관련되어야 함을 의미합니다. 고양이 사진을 입력했다면 모델이 생성한 이미지는 고양이여야 합니다. 강아지 사진을 입력했다면 모델이 생성한 이미지도 강아지와 관련이 있어야 합니다. x0을 제거하면 어떤 종류의 이미지 트레이닝이 입력되더라도 확산에 의해 생성된 최종 이미지는 "고양이와 개는 구별되지 않는다"는 것이 동일할 것입니다.

일련의 파생 후에 우리는 역과정의 매개변수

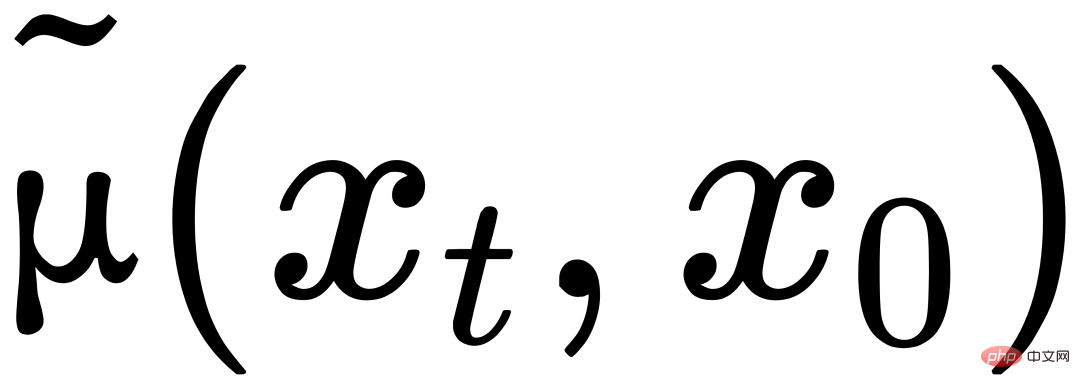
및

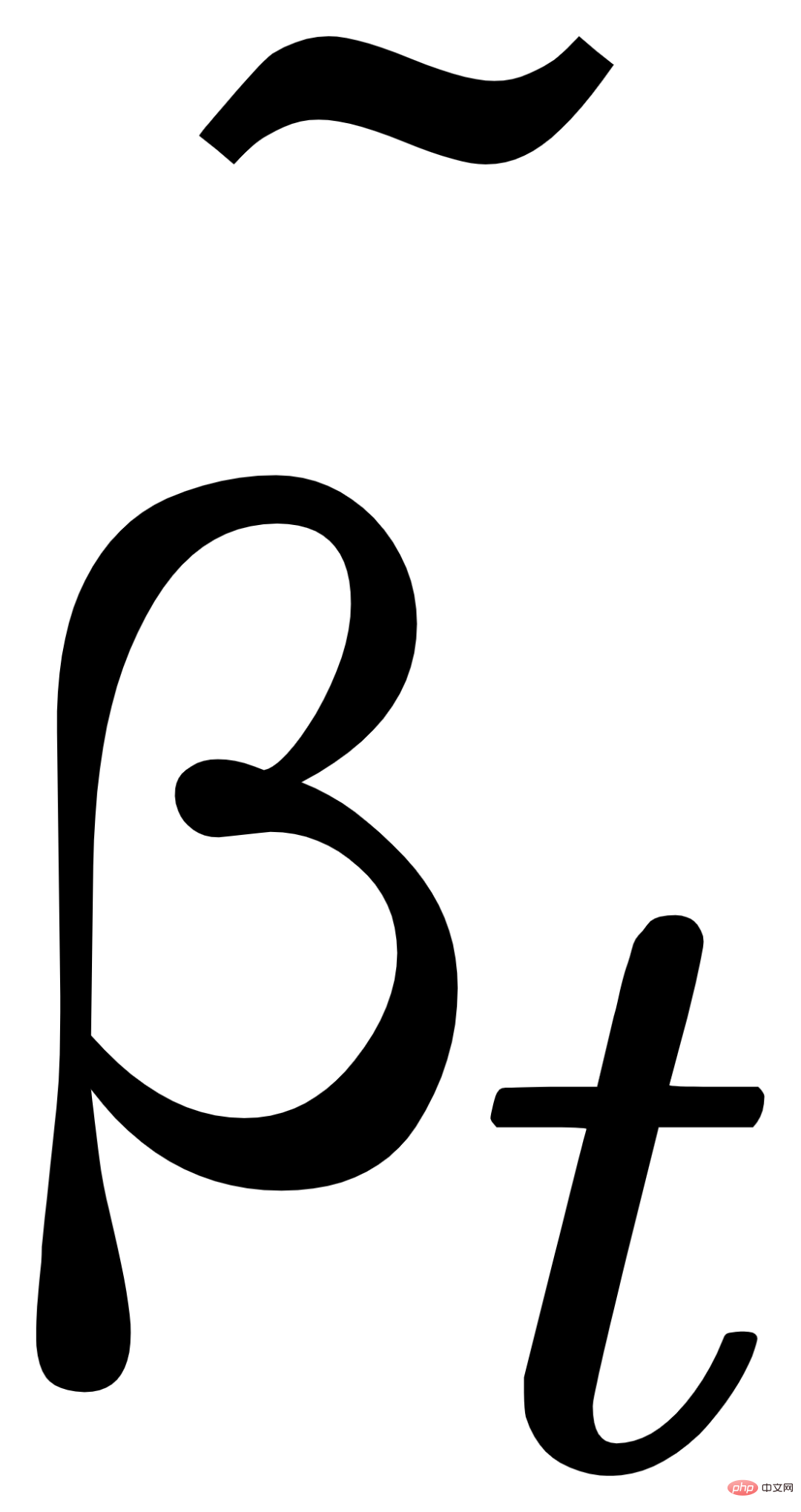
이 여전히 x0, xt 및 매개변수 βt로 표현될 수 있음을 발견했습니다. .

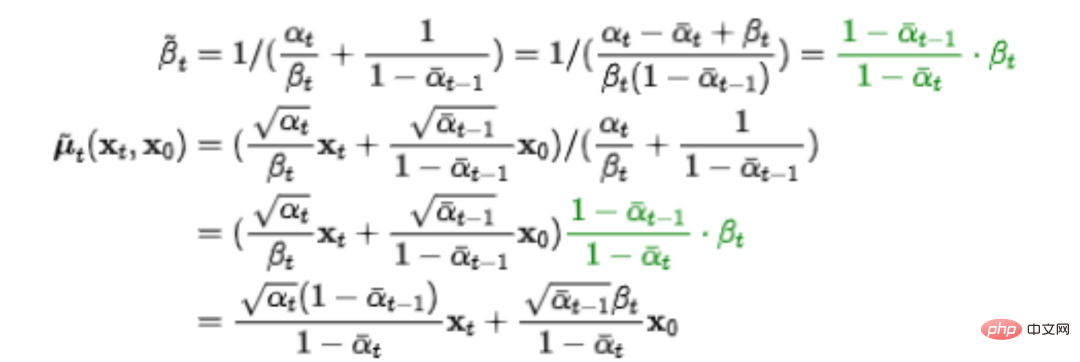
물론 기계는 실제 반전 과정을 미리 알지 못합니다. p0(xt-1|xt)로 표현되는 대략적인 추정 분포를 사용하여 시뮬레이션하는 것뿐입니다.

1.1.3 최적화 목표

처음에는 원본 데이터와 역과정을 통해 최종 생성된 데이터 간의 유사성을 높여 모델을 최적화해야 한다고 언급했습니다. 기계 학습에서는 교차 엔트로피를 기반으로 이러한 유사성을 계산합니다.

교차 엔트로피에 대한 학문적 정의는 "두 확률 분포 간의 차이 정보를 측정하는 데 사용됩니다"입니다. 즉, 교차 엔트로피가 작을수록 모델이 생성한 이미지가 원본 이미지에 더 가까워집니다. 그러나 대부분의 경우 교차 엔트로피는 계산이 어렵거나 불가능하므로 일반적으로 더 간단한 표현식을 최적화하여 동일한 효과를 얻습니다.

확산 모델은 VAE 모델의 최적화 아이디어를 활용하고 교차 엔트로피를 최대 최적화 목표인 변형 하한(VLB, ELBO라고도 함)으로 대체합니다. 수많은 분해 단계를 거친 후 마침내 다음과 같은 결과를 얻었습니다.

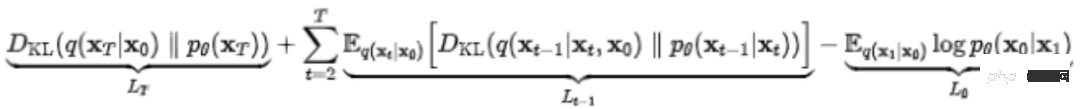
이렇게 복잡한 공식을 보면 많은 친구들이 머리가 큰 것 같습니다. 하지만 당황하지 마십시오. 여기서 주의해야 할 것은 중간에 있는 Lt-1입니다. 이는 추정 분포 p0(xt-1|xt)와 실제 분포 q(xt-1|xt,x0)를 나타냅니다. xt와 xt-1) 차이점. 간격이 작을수록 모델에서 생성된 최종 이미지가 더 좋습니다.

1.1.4 코드 업로드

DDPM의 원리를 이해한 후 DDPM 모델이 어떻게 구현되는지 살펴보겠습니다...

이상하네요. 나는 당신이 이 글을 읽을 때 수백, 수천 줄의 코드로 세례를 받고 싶지 않을 것이라고 믿습니다.

다행스럽게도 MindSpore는 완전히 개발된 DDPM 모델을 제공합니다. 작업은 간단하고 효과를 경험하고 싶은 친구만 있으면 됩니다

pip install denoising-diffusion-mindspore

그런 다음 다음 코드 구성 매개변수를 참조하세요.

중요 매개변수에 대한 일부 분석:

GaussianDiffusion

• image_size: 이미지 크기
• timesteps: 노이즈 단계 수
• sampling_timesteps: 추론 성능을 향상하려면 샘플링 단계 수보다 작아야 합니다. 노이즈 단계

Trainer

• folder_or_dataset: 그림의 경로에 해당하여 다운로드한 데이터 세트의 경로(str)일 수도 있고, 데이터 처리를 수행한 VisionBaseDataset, GeneratorDataset 또는 MindDataset일 수도 있습니다
• train_batch_size : 배치 크기
• train_lr: 학습률
• train_num_steps: 학습 단계 수

"고급 버전" DDPM 모델 MindDiffusion

DDPM은 Diffusion 이야기의 시작에 불과합니다. 현재 수많은 연구자들이 그 이면의 웅장한 세계에 매료되어 헌신하고 있습니다.

모델을 지속적으로 최적화하는 동시에 다양한 분야에서 확산의 응용도 점차 발전해 왔습니다.

여기에는 이미지 최적화, 인페인팅, 컴퓨터 비전 분야의 3D 비전, 자연어 처리 분야의 텍스트 음성 변환, 분자 형태 생성, 과학용 AI 분야의 재료 디자인 등이 포함됩니다.

스탠포드 대학교 컴퓨터공학과 박사과정 학생인 Eric Zelikman은 상상력을 발휘하여 DALLE-2와 최근 인기 있는 또 다른 대화 모델인 ChatGPT를 결합하여 마음이 따뜻해지는 그림책 이야기를 만들어 보았습니다.

ΔDALLE-2 + ChatGPT, "Robbie"라는 작은 로봇에 대한 이야기

하지만 가장 널리 알려진 것은 아마도 텍스트-이미지 변환 애플리케이션일 것입니다. 몇 가지 키워드나 간단한 설명을 입력하면 모델이 해당 그림을 생성할 수 있습니다.

예를 들어 "City Night Scene Cyberpunk Greg Lutkowsky"를 입력하면 최종 결과는 미래 SF 스타일의 밝은 색상의 작품이 됩니다.

또 다른 예를 들어 "달의 꿈에서 파라솔을 들고 있는 모네의 여인"이라고 입력하면 매우 흐릿한 여성의 초상화가 나올 것입니다. 컬러 매칭 스타일이 모네의 "수련"을 연상시키나요?

현실적인 풍경 사진을 화면 보호기로 사용하고 싶으십니까? 괜찮아요!

Δ컨트리 필드 스크린세이버

좀 더 2차원적인 집중력을 갖춘 것을 원하시나요? 그것도 괜찮아!

Δ심연 풍경화의 사실적인 스타일에서

위 사진은 모두 MindDiffusion 플랫폼 하의 Wukong Huahua에서 제작한 것입니다. Wukong Huahua는 확산 모델을 기반으로 Huawei의 Noah 팀이 만든 중국어 텍스트의 대형 모델입니다. ChinaSoft Distributed Parallel Laboratory 및 Ascend Computing Product Department와 협력하여 공동 개발했습니다.

이 모델은 Wukong 데이터 세트를 기반으로 훈련되었으며 MindSpore + Ascend 소프트웨어 및 하드웨어 솔루션을 사용하여 구현되었습니다.

시도해 보고 싶은 친구들은 걱정하지 마세요. 모두에게 더 나은 경험과 자기 개발을 위한 더 많은 공간을 제공하기 위해 MindDiffusion의 모델에도 훈련 가능성과 추론의 특성을 갖도록 만들 계획입니다. 내년에 출시될 예정입니다. 모두 기대해 주세요.

다양한 독창적인 스타일의 작품을 브레인스토밍하고 만들어내는 여러분을 환영합니다~

(내부 정보를 문의하러 갔던 동료들에 따르면 이미 "장비 자수", "유화강 멜론 자르기", " 고대 그리스 신들" "고질라 vs. 고질라". 음, 어떡하지? 문득 완성품이 기대되네요(ಡΩಡ))

한 가지 더

마지막으로 디퓨전이 인기를 끌면서 몇몇 분들도 왜 GAN 네트워크보다 더 인기를 끌기 시작할 만큼 인기를 얻을 수 있는지 물었습니다.

확산에는 뛰어난 장점과 명백한 단점이 있습니다. 많은 분야가 아직 비어 있고 미래도 아직 알 수 없습니다.

왜 이렇게 쉬지 않고 일하는 사람들이 많은 걸까요?

아마 이 교수님의 말씀이 우리에게 답을 줄 수도 있을 것입니다.

그러나 확산 프로세스의 효율성과 GAN의 신속한 교체는 또한 간단한 진실을 완전히 보여줍니다.

몇 줄의 간단하고 정확한 수학적 파생은 하이퍼 매개변수의 대규모 디버깅 및 네트워크 디버깅보다 훨씬 더 효과적일 수 있습니다. 지난 10년간의 구조.

아마 이것이 디퓨전 모델의 매력이 아닐까 싶습니다.

参考链接（可滑动查看）：

[1]https://medium.com/mlearning-ai/ai-art-wins-fine-arts-competition-and-sparks-controversy-882f9b4df98c

[2] 조나단 호, 아제이 제인, 피터 아빌. 노이즈 제거 확산 확률 모델. arXiv:2006.11239, 2020.

[3]Ling Yang, Zhilong Zhang, Shenda Hong, Runsheng Xu, Yue Zhao, Yingxia Shao, Wentao Zhang, Ming-Hsuan Yang 및 Bin Cui. 확산 모델: 방법 및 적용에 대한 포괄적인 조사입니다. arXiv 사전 인쇄 arXiv:2209.00796, 2022.

[4]https://lilianweng.github.io/posts/2021-07-11-diffusion-models

[5]https://github.com/lvyufeng/denoising -확산-마음포자

[6]https://zhuanlan.zhihu.com/p/525106459

[7]https://zhuanlan.zhihu.com/p/500532271

[8]https://www .zhihu.com/question/536012286

[9]https://mp.weixin.qq.com/s/XTNk1saGcgPO-PxzkrBnIg

[10]https://m.weibo.cn/3235040884/4804448864177745

위 내용은 카드 하나로 AI 페인팅 모델을 실행할 수 있습니다. 초보자도 이해할 수 있는 튜토리얼이 100만 장의 카드로 제공됩니다.의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!