시계열 특징 추출을 위한 Python 및 Pandas 코드 예제

Pandas와 Python을 사용하여 이동 평균, 자기 상관, 푸리에 변환 등 시계열 데이터에서 의미 있는 특징을 추출합니다.

머리말

시계열 분석은 다양한 산업(예: 금융, 경제, 의료 등)의 추세를 이해하고 예측하는 강력한 도구입니다. 특징 추출은 원시 데이터를 예측 및 분석을 위해 모델을 훈련하는 데 사용할 수 있는 의미 있는 특징으로 변환하는 과정을 포함하는 이 프로세스의 핵심 단계입니다. 이 기사에서는 Python과 Pandas를 사용하여 시계열 특징 추출 기술을 살펴보겠습니다.

특징 추출에 앞서 시계열 데이터에 대해 간단히 살펴보겠습니다. 시계열 데이터는 시간 순서로 색인된 일련의 데이터 포인트입니다. 시계열 데이터의 예로는 주가, 기온 측정, 교통 데이터 등이 있습니다. 시계열 데이터는 단변량 또는 다변량일 수 있습니다. 일변량 시계열 데이터에는 변수가 하나만 있는 반면, 다변량 시계열 데이터에는 변수가 여러 개 있습니다.

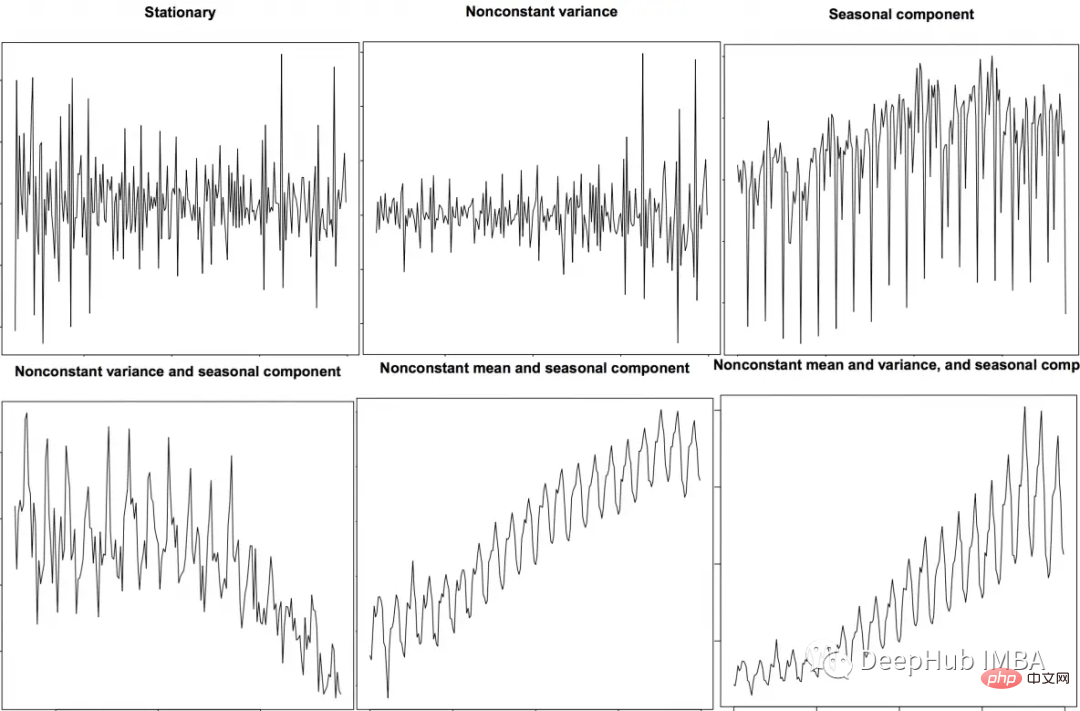
시계열 분석에 사용할 수 있는 다양한 특징 추출 기법이 있습니다. 이 기사에서는 다음 기술을 소개합니다.

• Resampling
• Moving Average
• Exponential Smoothing
• Autocorrelation
• Fourier Transform

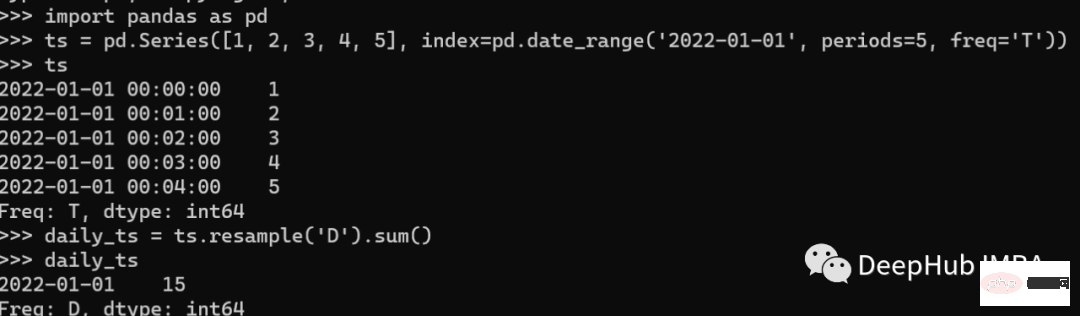
1 Resampling은 주로 시계열 데이터의 빈도를 변경합니다. 이는 노이즈를 평활화하거나 데이터를 더 낮은 주파수로 샘플링하는 데 유용합니다. Pandas는 시계열 데이터를 리샘플링하는 resample() 메서드를 제공합니다. resample() 메서드를 사용하여 데이터를 업샘플링하거나 다운샘플링할 수 있습니다. 다음은 시계열을 일별 빈도로 다운샘플링하는 방법에 대한 예입니다.

import pandas as pd
 
 # create a time series with minute frequency
 ts = pd.Series([1, 2, 3, 4, 5], index=pd.date_range('2022-01-01', periods=5, freq='T'))
 
 # downsample to daily frequency
 daily_ts = ts.resample('D').sum()
 
 print(daily_ts)

위의 예에서는 분 단위의 빈도로 시계열을 생성한 다음 resample() 메서드를 사용하여 일별 빈도로 샘플링했습니다.

2. 이동 평균

이동 평균 이동 평균은 롤링 윈도우에 대한 평균을 계산하여 시계열 데이터를 평활화하는 기술입니다. 노이즈를 제거하고 데이터의 추세를 파악하는 데 도움이 될 수 있습니다. Pandas는 시계열의 평균을 계산하는 Rolling() 메서드를 제공합니다. 다음은 시계열의 평균을 계산하는 방법에 대한 예입니다.

import pandas as pd
 
 # create a time series
 ts = pd.Series([1, 2, 3, 4, 5])
 
 # calculate the rolling mean with a window size of 3
 rolling_mean = ts.rolling(window=3).mean()
 
 print(rolling_mean)

시계열을 생성한 다음 Rolling() 메서드를 사용하여 창 크기 3으로 이동 평균을 계산합니다.

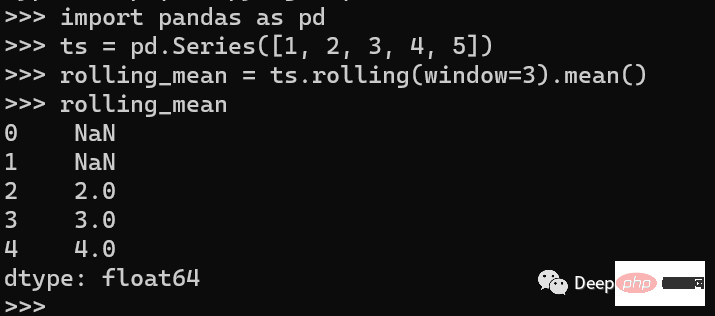처음 두 값은 이동 평균의 최소 개수인 3에 도달하지 못하기 때문에 NAN이 생성되는 것을 볼 수 있습니다. 필요한 경우 fillna 방법을 사용하여 채울 수 있습니다.

3. 지수평활

지수평활은 최근 값에 더 많은 가중치를 부여하여 시계열 데이터를 평활화하는 기술입니다. 이는 노이즈를 제거하고 데이터의 추세를 얻는 데 도움이 될 수 있습니다. Pandas는 지수 이동 평균을 계산하기 위한 ewm() 메서드를 제공합니다.

import pandas as pd
 ts = pd.Series([1, 2, 3, 4, 5])
 ts.ewm( alpha =0.5).mean()

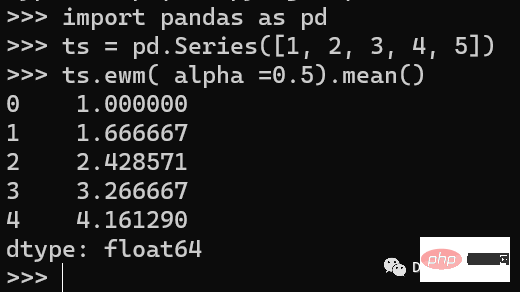위의 예에서는 시계열을 만든 다음 ewm() 메서드를 사용하여 평활화 계수 0.5로 지수 이동 평균을 계산했습니다.

ewm에는 많은 매개변수가 있는데 여기서는 몇 가지 주요 매개변수를 소개합니다.

com: 질량 중심을 기준으로 감쇠 지정

span 범위를 기준으로 감쇠 지정

halflife 반감기를 기준으로 감쇠 지정

alpha 평활화 계수 α 지정

위 4개의 매개변수는 모두 평활화 계수 α를 지정하지만 처음 3개는 조건에 따라 계산되고 마지막은 수동으로 지정되므로 최소한 예를 들어 위의 예에서는 수동으로 0.5를 직접 설정했습니다.

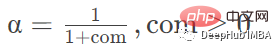
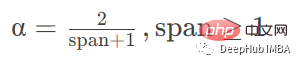
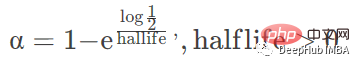
min_기간 창에 값이 있는 최소 관측 수, 기본값은 0입니다.

adjust 오류 수정 수행 여부. 기본값은 True입니다.

adjust =Ture时公式如下：

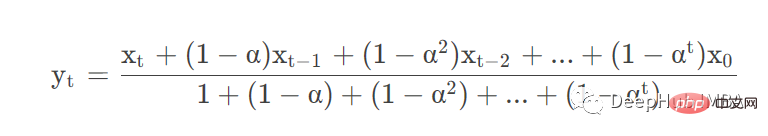
adjust =False

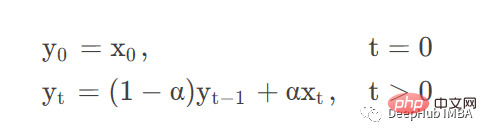
4、Autocorrelation

Autocorrelation 自相关是一种用于测量时间序列与其滞后版本之间相关性的技术。可以识别数据中重复的模式。Pandas提供了autocorr()方法来计算自相关性。

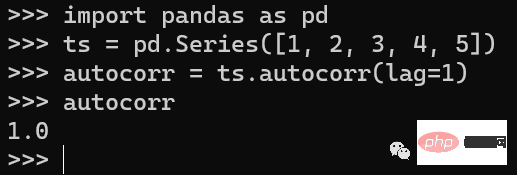
import pandas as pd
 
 # create a time series
 ts = pd.Series([1, 2, 3, 4, 5])
 
 # calculate the autocorrelation with a lag of 1
 autocorr = ts.autocorr(lag=1)
 
 print(autocorr)

5、Fourier Transform

Fourier Transform 傅里叶变换是一种将时间序列数据从时域变换到频域的技术。可以识别数据中的周期性模式。我们可以使用numpy的fft()方法来计算时间序列的快速傅里叶变换。

import pandas as pd
 import numpy as np
 
 # create a time series
 ts = pd.Series([1, 2, 3, 4, 5])
 
 # calculate the Fourier transform
 fft = pd.Series(np.fft.fft(ts).real)
 
 print(fft)

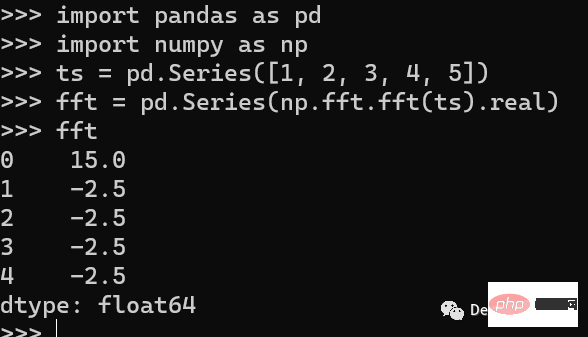
这里我们只显示了实数的部分。

总结

在本文中，我们介绍了几种使用Python和Pandas的时间序列特征提取技术。这些技术可以帮助将原始时间序列数据转换为可用于分析和预测的有意义的特征，在训练机器学习模型时，这些特征都可以当作额外的数据输入到模型中，可以增加模型的预测能力。

위 내용은 시계열 특징 추출을 위한 Python 및 Pandas 코드 예제의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!