희소 모델의 최신 진전! Ma Yi + LeCun이 힘을 합치다: '화이트 박스' 비지도 학습
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWB앞으로
- 2023-04-12 08:34:021006검색
최근 Ma Yi 교수와 Turing Award 수상자 Yann LeCun은 ICLR 2023에서 공동으로 논문을 발표했습니다. 이 논문에서는 데이터 향상이나 하이퍼매개변수 조정 또는 기타 엔지니어링 설계에 의존할 필요가 없는 최소한의 해석 가능한 비지도 학습 방법을 설명합니다. SOTA SSL 방식.

문서 링크: https://arxiv.org/abs/2209.15261
이 방법은 희소 다양체 변환을 사용하여 희소 코딩, 다양체 학습 및 느린 기능을 결합합니다. 기능 분석)이 결합되었습니다.
단일 레이어 결정적 희소 다양체 변환을 사용하면 MNIST에서 99.3% KNN top-1 정확도, CIFAR-10에서 81.1% KNN top-1 정확도, CIFAR-100에서 81.1% KNN top-1 정확도를 달성할 수 있습니다. .KNN top-1 정확도 53.2%를 달성했습니다.
간단한 그레이스케일 향상을 통해 CIFAR-10과 CIFAR-100의 모델 정확도는 각각 83.2%와 57%에 이르렀습니다. 이러한 결과는 단순한 "화이트 박스" 방식과 SOTA 방식 간의 격차를 크게 줄였습니다. .
또한 이 기사에서는 비지도 표현 변환을 형성하는 방법에 대한 시각적 설명도 제공합니다. 이 방법은 latent embedding self-supervised 방법과 밀접한 관련이 있으며 가장 간단한 VICReg 방법이라고 볼 수 있습니다.

간단한 구성 모델과 SOTA 접근 방식 사이에는 여전히 작은 성능 차이가 있지만 이것이 원칙에 입각한 화이트박스 비지도 학습을 달성하기 위한 유망한 방향이라는 증거가 있습니다.
이 기사의 첫 번째 저자인 Yubei Chen은 뉴욕 대학교 데이터 과학 센터(CDS) 및 메타 기초 인공 지능 연구(FAIR)에서 박사후 연구원으로 근무하고 있습니다. 그의 지도교수는 Yann LeCun 교수입니다. 캘리포니아 대학교 버클리 과학 캠퍼스의 레드우드 센터와 버클리 인공 지능 연구소(BAIR)에서 이론 신경학 박사 학위를 취득했으며 칭화대학교에서 학사 학위를 취득했습니다.

주요 연구 방향은 계산 신경과학 학습과 심층 비지도(자기 지도) 학습의 교차점입니다. 연구 결과는 뇌와 기계에서 비지도 표현 학습의 계산 원리에 대한 이해를 높이고, 자연 신호의 통계에 대한 이해.
Ma Yi 교수는 1995년 칭화대학교에서 자동화 및 응용수학 이중 학사 학위를 취득했고, 1997년 캘리포니아 버클리 대학교에서 EECS 석사 학위를 받았으며, 2009년 EECS에서 수학 석사 및 박사 학위를 받았습니다. 2000. 그는 현재 캘리포니아대학교 버클리캠퍼스 전기공학 및 컴퓨터공학과 교수로 재직하고 있으며, IEEE 펠로우, ACM 펠로우, SIAM 펠로우이기도 합니다.
Yann LeCun의 가장 유명한 작품은 광학 문자 인식 및 컴퓨터 비전에 CNN(컨볼루션 신경망)을 사용한 것입니다. 그는 2019년에 Bengio와 Hinton이 공동으로 최고상을 받았습니다. 컴퓨터 과학상 Turing Award에서 영예를 안았습니다.
가장 간단한 비지도 학습부터 시작하세요
비지도 표현 학습은 지난 몇 년 동안 엄청난 발전을 이루었으며 데이터 기반 기계 학습에서 강력한 확장성을 제공할 것으로 예상됩니다.
그러나 학습된 표현이 무엇인지, 그것이 비지도 방식으로 정확히 어떻게 형성되는지는 여전히 불분명하며, 이러한 모든 비지도 표현을 뒷받침하는 공통 원칙이 있는지도 여전히 불분명합니다.
많은 연구자들이 모델 이해 향상의 중요성을 인식하고 SOTA 방법을 단순화하고, 고전적인 방법과의 연결을 설정하고, 다양한 방법을 통합하고, 표현을 시각화하고, 이론적 관점에서 이러한 방법을 분석하기 위한 몇 가지 선구적인 조치를 취했습니다. , 다른 계산 이론을 개발하기 위한 희망으로: 첫 번째 원리를 기반으로 데이터에서 간단하고 완전히 해석 가능한 "화이트 박스" 모델을 구축할 수 있으며 이에 대한 통찰력도 제공할 수 있습니다. 인간 두뇌의 비지도 학습 원리는 지침을 제공합니다. .
이 연구에서 연구원들은 딥 네트워크, 프로젝션 헤드, 데이터 증강 또는 기타 다양한 엔지니어링 설계가 필요하지 않은 가장 간단한 "화이트 박스" 비지도 학습 모델을 구축하려고 노력하면서 이 목표를 향한 또 다른 작은 발걸음을 내디뎠습니다.
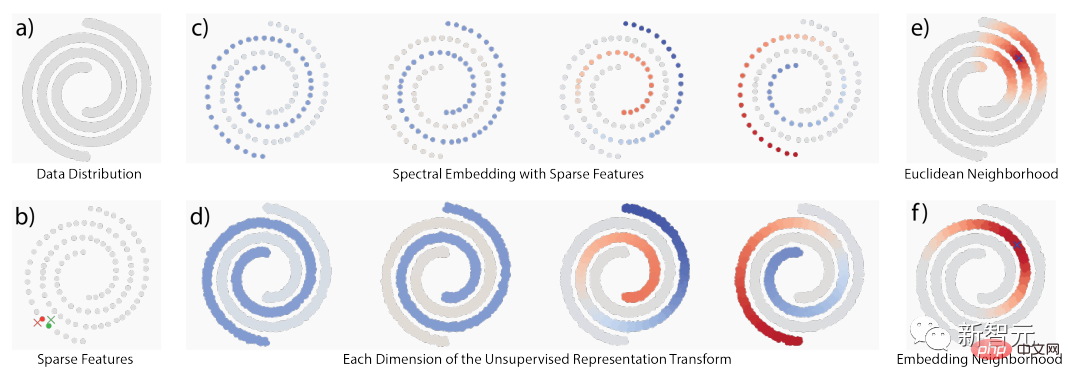
희소성과 스펙트럼 임베딩이라는 두 가지 고전적인 비지도 학습 원리를 활용하여 2계층 모델을 구축하고 여러 표준 데이터 세트에서 중요하지 않은 기준 결과를 달성합니다.
실험 결과 희소 다양체 변환을 기반으로 한 2계층 모델은 잠재 임베딩 자기 지도 방법과 동일한 목표를 갖고 있으며 데이터 증강 없이 MNIST에서 최고의 성능을 달성하는 것으로 나타났습니다. KNN의 최고 레벨 1 정확도 는 99.3%이며, KNN의 최고 레벨 1 정확도는 CIFAR-10에서 81.1%, CIFAR-100에서는 53.2%이다.
간단한 그레이스케일 향상을 통해 CIFAR-10에서 83.2% KNN top-1 정확도, CIFAR-100에서 57% KNN top-1 정확도를 달성했습니다.
이러한 결과는 "화이트 박스" 모델과 SOTA 자체 감독(SSL) 모델 사이의 격차를 줄이는 데 중요한 단계입니다. 비록 격차가 여전히 상당하지만 연구원들은 격차를 더욱 좁히면 개선될 가능성이 있다고 믿습니다. 감독되지 않은 표현. 더 깊은 이해를 얻는 방법을 배우는 것도 이 이론의 실제 적용으로 이어지는 유망한 연구 경로입니다.
세 가지 기본 질문
무지도(자기 지도) 재표현이란 무엇입니까
본질적으로 원래 신호의 모든 비식별 변환은 재표현이라고 할 수 있지만, 학자들은 유용한 변환에 더 관심이 있습니다.
비지도 재현 학습의 거시적 목표는 "유사한" 것들이 동시에 더 가까이 배치되도록 원본 데이터를 새로운 공간으로 변환하는 기능을 찾는 것입니다. 즉, 데이터의 기하학적 또는 무작위 구조가 보존되어야 합니다.
이 목표가 달성되면 '이질적인' 콘텐츠는 자연스럽게 표현 공간에서 멀리 배치됩니다.
유사성은 어디서 오는 걸까요?
유사성은 주로 1) 시간적 동시 발생, 2) 공간적 동시 발생, 3) 원래 신호 공간의 지역적 이웃이라는 세 가지 고전적인 아이디어에서 비롯됩니다.
기본 구조가 기하학적 구조인 경우 이러한 아이디어는 상당히 중복되지만 구조가 무작위 구조인 경우 개념적으로도 다릅니다.) 및 확률론적 동시 발생. 구조.
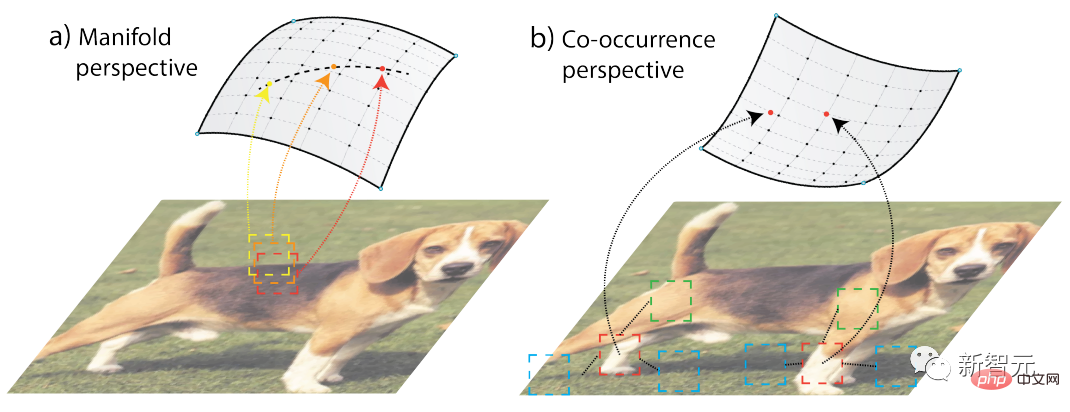
관련 작업에서는 두 가지 비지도 학습 방법인 다양체 학습과 동시 발생 통계 모델링을 제안하며 이러한 아이디어 중 상당수가 계보 분해 또는 밀접하게 관련된 행렬의 공식화에 도달했습니다.
다양한 학습의 개념은 원래의 신호 공간에 있는 지역 동네만 신뢰할 수 있다는 것입니다. 모든 지역 동네를 종합적으로 고려함으로써 글로벌 기하학, 즉 "글로벌 사고, 로컬 적응"(생각은 글로벌하게, 로컬에 적합)이 등장합니다. ).
반대로 동시 발생 통계 모델링은 확률적 개념을 따릅니다. 일부 구조는 연속 다양체로 모델링할 수 없기 때문에 다양체 개념을 보완하기도 합니다.
가장 분명한 예 중 하나는 원본 데이터가 기본적으로 부드러운 기하학에서 나오지 않는 자연어에서 나옵니다. 예를 들어 단어 임베딩에서 "Seattle"과 "Dallas"의 임베딩은 매우 유사할 수 있습니다. 하지만 동시 발생이 빈번한 근본적인 이유는 유사한 맥락 패턴을 가지고 있기 때문입니다.
"유사성"을 이해하는 데 있어 확률과 다양체의 관점은 서로 보완적입니다. 일단 유사성에 대한 정의가 있으면 유사한 개념을 더 가깝게 만드는 변환을 구성할 수 있습니다.
이 기사에서 표현 변환을 설정하는 방법은 무엇입니까? 기본 원칙: 희소성 및 낮은 순위
일반적으로 희소성은 지원을 설정하기 위해 데이터 공간의 지역성과 분해를 처리하는 데 사용될 수 있으며, 그런 다음 저빈도 함수를 사용하여 유사한 변환을 위한 표현 변환을 구성합니다. 지원의 유사점에 할당됩니다.
전체 프로세스를 희소 다양체 변환이라고도 합니다.
위 내용은 희소 모델의 최신 진전! Ma Yi + LeCun이 힘을 합치다: '화이트 박스' 비지도 학습의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!

