믿을 수 없는! Numpy를 사용하여 딥러닝 프레임워크를 개발하고 신경망 훈련 프로세스를 살펴봅니다.

안녕하세요 여러분.

오늘 저는 Numpy를 사용하여 딥 러닝 프레임워크를 개발한 매우 멋진 오픈 소스 프로젝트를 여러분과 공유하고 싶습니다. 구문은 기본적으로 Pytorch와 동일합니다.

오늘은 간단한 컨벌루션 신경망을 예로 들어 순전파, 역전파, 매개변수 최적화 등 신경망 훈련 과정에 관련된 핵심 단계의 소스 코드를 분석합니다.

사용된 데이터 세트와 코드는 패키지로 제공되어 있으며, 기사 마지막 부분에서 이를 얻을 수 있는 방법이 있습니다.

1. 준비

먼저 데이터와 코드를 준비합니다.

1.1 네트워크 구축

먼저 프레임워크 소스 코드를 다운로드합니다. 주소는 https://github.com/duma-repo/PyDyNet

git clone https://github.com/duma-repo/PyDyNet.git

LeNet 컨볼루션 신경망을 구축하고 3분류 모델을 훈련합니다.

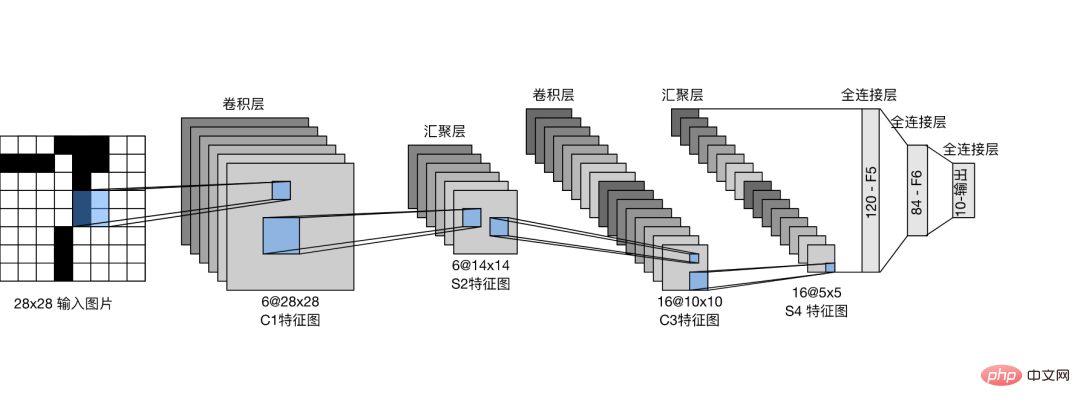
PyDyNet 디렉터리에 직접 코드 파일을 만듭니다.

from pydynet import nn

class LeNet(nn.Module):
def __init__(self):
super().__init__()
self.conv1 = nn.Conv2d(1, 6, kernel_size=5, padding=2)
self.conv2 = nn.Conv2d(6, 16, kernel_size=5)
self.avg_pool = nn.AvgPool2d(kernel_size=2, stride=2, padding=0)
self.sigmoid = nn.Sigmoid()
self.fc1 = nn.Linear(16 * 5 * 5, 120)
self.fc2 = nn.Linear(120, 84)
self.fc3 = nn.Linear(84, 3)

def forward(self, x):
x = self.conv1(x)
x = self.sigmoid(x)
x = self.avg_pool(x)

x = self.conv2(x)
x = self.sigmoid(x)
x = self.avg_pool(x)

x = x.reshape(x.shape[0], -1)

x = self.fc1(x)
x = self.sigmoid(x)
x = self.fc2(x)
x = self.sigmoid(x)
x = self.fc3(x)

return x

네트워크의 정의가 Pytorch 구문과 정확히 동일하다는 것을 알 수 있습니다.

제가 제공한 소스코드에는 네트워크 구조를 출력할 수 있는 요약 기능이 제공되어 있습니다.

1.2 데이터 준비

훈련 데이터는 Fanshion-MNIST 데이터 세트를 사용합니다. 여기에는 10개의 사진 카테고리, 각 카테고리에 6k ​​이미지가 포함되어 있습니다.

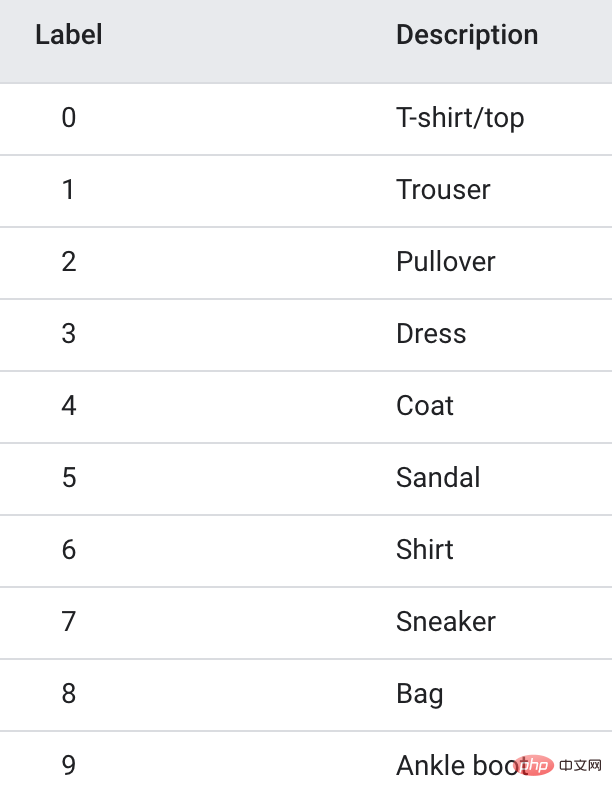
학습 속도를 높이기 위해 처음 3개 카테고리만 추출하여 총 1.8w의 학습 이미지를 만들어 3분류 모델을 만들었습니다.

1.3 모델 훈련

import pydynet
from pydynet import nn
from pydynet import optim

lr, num_epochs = 0.9, 10
optimizer = optim.SGD(net.parameters(),
lr=lr)
loss = nn.CrossEntropyLoss()

for epoch in range(num_epochs):
net.train()
for i, (X, y) in enumerate(train_iter):
optimizer.zero_grad()
y_hat = net(X)
l = loss(y_hat, y)
l.backward()
optimizer.step()

with pydynet.no_grad():
metric.add(l.numpy() * X.shape[0],
 accuracy(y_hat, y),
 X.shape[0])

훈련 코드도 Pytorch와 동일합니다.

다음으로 해야 할 중요한 일은 모델 훈련의 소스 코드를 자세히 살펴보고 모델 훈련의 원리를 배우는 것입니다.

2. train, no_grad 및 eval

net.train은 모델이 훈련을 시작하기 전에 호출됩니다.

def train(self, mode: bool = True):
set_grad_enabled(mode)
self.set_module_state(mode)

grad(gradient)가 True로 설정되고 이후에 생성된 Tensor가 그래디언트를 가질 수 있음을 알 수 있습니다. Tensor가 기울기를 가져온 후 계산 그래프에 넣고 파생이 기울기를 계산할 때까지 기다립니다.

다음 no_grad(): 코드

class no_grad:
def __enter__(self) -> None:
self.prev = is_grad_enable()
set_grad_enabled(False)

는 grad​(gradient)를 False​로 설정하므로 나중에 생성된 Tensor는 계산 그래프에 배치되지 않으며 당연히 기울기를 계산할 필요가 없습니다. 추론 속도를 높일 수 있습니다.

Pytorch에서 net.eval()의 사용법을 자주 볼 수 있으며, 소스 코드도 살펴봅니다.

def eval(self):
return self.train(False)

train(False)을 직접 호출하여 그래디언트를 끄는 것을 볼 수 있으며 그 효과는 no_grad()와 유사합니다.

따라서 일반적으로 훈련 전에 train을 호출하여 그라데이션을 켜세요. 훈련 후에는 빠른 추론을 촉진하기 위해 eval을 호출하여 기울기를 닫습니다.

3. 순방향 전파

순방향 전파에서 가장 중요한 것은 순방향 전파 순서에 따라 네트워크의 텐서를 정리하는 것입니다. 역전파 중 텐서의 기울기.

신경망의 Tensor는 데이터를 저장하는 데뿐만 아니라 기울기를 계산하고 저장하는 데도 사용됩니다.

계산 그래프를 생성하는 방법을 보려면 첫 번째 레이어 컨볼루션 작업을 예로 들어보세요.

def conv2d(x: tensor.Tensor,
 kernel: tensor.Tensor,
 padding: int = 0,
 stride: int = 1):
'''二维卷积函数
'''
N, _, _, _ = x.shape
out_channels, _, kernel_size, _ = kernel.shape
pad_x = __pad2d(x, padding)
col = __im2col2d(pad_x, kernel_size, stride)
out_h, out_w = col.shape[-2:]
col = col.transpose(0, 4, 5, 1, 2, 3).reshape(N * out_h * out_w, -1)
col_filter = kernel.reshape(out_channels, -1).T
out = col @ col_filter
return out.reshape(N, out_h, out_w, -1).transpose(0, 3, 1, 2)

x​는 입력 이미지이며 그라데이션을 기록할 필요가 없습니다. 커널은 컨볼루션 커널의 가중치이며 기울기를 계산해야 합니다.

따라서 pad_x = __pad2d(x, padding)​에 의해 생성된 새 텐서에도 그라데이션이 없으므로 계산 그래프에 추가할 필요가 없습니다.

kernel.reshape(out_channels, -1)​에 의해 생성된 텐서는 기울기를 계산해야 하며 계산 그래프에도 추가해야 합니다.

조인 프로세스를 살펴보겠습니다.

def reshape(self, *new_shape):
return reshape(self, new_shape)

class reshape(UnaryOperator):
'''
张量形状变换算子，在Tensor中进行重载

Parameters
----------
new_shape : tuple
变换后的形状，用法同NumPy
'''
def __init__(self, x: Tensor, new_shape: tuple) -> None:
self.new_shape = new_shape
super().__init__(x)

def forward(self, x: Tensor)
return x.data.reshape(self.new_shape)

def grad_fn(self, x: Tensor, grad: np.ndarray)
return grad.reshape(x.shape)

reshape​ 함수는 reshape​ 클래스 객체를 반환합니다. reshape​ 클래스는 UnaryOperator​ 클래스를 상속하고 __init__ 함수에서는 상위 클래스 초기화 함수가 호출됩니다.

class UnaryOperator(Tensor):
def __init__(self, x: Tensor) -> None:
if not isinstance(x, Tensor):
x = Tensor(x)
self.device = x.device
super().__init__(
data=self.forward(x),
device=x.device,
# 这里 requires_grad 为 True
requires_grad=is_grad_enable() and x.requires_grad,
)

UnaryOperator 클래스는 Tensor 클래스를 상속하므로 reshape 객체도 텐서입니다.

UnaryOperator의 __init__​ 함수에서 Tensor의 초기화 함수가 호출되고 전달된 필수_grad 매개변수가 True이므로 기울기를 계산해야 함을 의미합니다.

requires_grad​의 계산 코드는 is_grad_enable()이고 x.requires_grad.is_grad_enable()​은 열차에 의해 True로 설정되었으며 x​는 컨볼루션 커널이고 require_grad​도 True입니다.

class Tensor:
def __init__(
self,
data: Any,
dtype=None,
device: Union[Device, int, str, None] = None,
requires_grad: bool = False,
) -> None:
if self.requires_grad:
# 不需要求梯度的节点不出现在动态计算图中
Graph.add_node(self)

마지막으로 Tensor 클래스의 초기화 메소드에서 Graph.add_node(self)를 호출하여 현재 텐서를 계산 그래프에 추가합니다.

마찬가지로, require_grad=True인 텐서를 사용하여 아래에서 흔히 볼 수 있는 새로운 텐서가 계산 그래프에 배치됩니다.

컨볼루션 작업 후 계산 그래프에 6개의 노드가 추가됩니다.

4. 역전파

한 번의 순방향 전파가 완료된 후 계산 그래프의 마지막 노드부터 시작하여 뒤에서 앞으로 역전파를 수행합니다.

l = loss(y_hat, y)
l.backward()

는 순방향 네트워크를 통해 레이어별로 전파되고 최종적으로 손실 텐서 l에 도달합니다.

l을 시작점으로 하고 앞에서 뒤로 전파하면 계산 그래프에서 각 노드의 기울기를 계산할 수 있습니다.

backward의 핵심 코드는 다음과 같습니다.

def backward(self, retain_graph: bool = False):

for node in Graph.node_list[y_id::-1]:
grad = node.grad
for last in [l for l in node.last if l.requires_grad]:
add_grad = node.grad_fn(last, grad)

last.grad += add_grad

Graph.node_list[y_id::-1]는 계산 그래프를 역순으로 정렬합니다.

node​是前向传播时放入计算图​中的每个tensor。

node.last​ 是生成当前tensor的直接父节点。

调用node.grad_fn计算梯度，并反向传给它的父节点。

grad_fn​其实就是Tensor的求导公式，如：

class pow(BinaryOperator):
'''
幂运算算子，在Tensor类中进行重载

See also
--------
add : 加法算子
'''
def grad_fn(self, node: Tensor, grad: np.ndarray)
if node is self.last[0]:
return (self.data * self.last[1].data / node.data) * grad

return​后的代码其实就是幂函数求导公式。

假设y=x^2，x​的导数为2x。

5. 更新参数

反向传播计算梯度后，便可以调用优化器，更新模型参数。

l.backward()
optimizer.step()

本次训练我们用梯度下降SGD算法优化参数，更新过程如下：

def step(self):
for i in range(len(self.params)):
grad = self.params[i].grad + self.weight_decay * self.params[i].data
self.v[i] *= self.momentum
self.v[i] += self.lr * grad
self.params[i].data -= self.v[i]
if self.nesterov:
self.params[i].data -= self.lr * grad

self.params​是整个网络的权重，初始化SGD时传进去的。

step​函数最核心的两行代码，self.v[i] += self.lr * grad​ 和 self.params[i].data -= self.v[i]​，用当前参数 - 学习速率 * 梯度​更新当前参数。

这是机器学习的基础内容了，我们应该很熟悉了。

一次模型训练的完整过程大致就串完了，大家可以设置打印语句，或者通过DEBUG的方式跟踪每一行代码的执行过程，这样可以更了解模型的训练过程。

위 내용은 믿을 수 없는! Numpy를 사용하여 딥러닝 프레임워크를 개발하고 신경망 훈련 프로세스를 살펴봅니다.의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!