확산 모델 뒤에 숨은 수학은 소화하기 너무 어렵나요? Google은 통일된 관점으로 이를 명확하게 설명합니다.
- 王林앞으로
- 2023-04-11 19:46:081243검색
최근 AI 페인팅이 큰 인기를 끌고 있습니다.
AI의 페인팅 능력에 감탄하면서도 확산 모델이 큰 역할을 한다는 사실은 모르고 계실 수도 있습니다. 인기 모델인 OpenAI의 DALL·E 2를 예로 들어 보겠습니다. 간단한 텍스트(프롬프트)만 입력하면 1024*1024 고화질 이미지를 여러 개 생성할 수 있습니다.
DALL·E 2가 발표된 지 얼마 지나지 않아 Google은 주어진 텍스트 설명에서 장면의 사실적인 이미지를 생성할 수 있는 텍스트-이미지 AI 모델인 Imagen을 출시했습니다.
몇일 전 Stability.Ai는 텍스트 생성 이미지 모델 Stable Diffusion의 최신 버전을 공개했으며, 이를 통해 생성된 이미지는 상용 등급에 도달했습니다.
Google이 2020년 DDPM을 출시한 이후 확산형 모델이 점차 세대 분야에서 새로운 핫스팟이 되었습니다. 이후 OpenAI는 GLIDE, ADM-G 모델 등을 출시하여 확산 모델을 대중화했습니다.
많은 연구자들은 확산 모델 기반의 텍스트 이미지 생성 모델이 매개변수 수가 적을 뿐만 아니라 더 높은 품질의 이미지를 생성하고 GAN을 대체할 가능성이 있다고 믿고 있습니다.
그러나 확산 모델의 수학적 공식은 많은 연구자들에게 부담이 되었으며, 많은 연구자들은 VAE 및 GAN보다 이해하기가 훨씬 더 어렵다고 믿습니다.
최근 Google Research의 한 연구원이 "확산 모델 이해: 통합된 관점"이라는 글을 썼습니다. 이 글은 다른 연구자들이 따라하고 이해할 수 있도록 확산 모델의 수학적 원리를 매우 상세한 방식으로 보여줍니다. 확산 모델이 무엇이며 어떻게 작동하는지. 
논문 주소: https://arxiv.org/pdf/2208.11970.pdf 이 논문이 얼마나 "수학적"인지에 대해 저자는 다음과 같이 설명합니다. 우리와 그 극심한 세부 사항 )은 이 논문 뒤에 있는 수학을 보여줍니다. 모델.
이 논문은 주로 생성 모델, VAE 및 계층적 VAE 점수 기반 생성 모델 등을 포함하여 6개 부분으로 구성됩니다.
다음은 소개용 논문에서 발췌한 내용입니다.
생성 모델
분포에 관찰 샘플 x가 주어지면 생성 모델의 목표는 실제 데이터를 학습하는 것입니다. 분포 p( x ) 모델링. 모델이 학습된 후에는 새로운 샘플을 생성할 수 있습니다. 또한 일부 형태에서는 학습 모델을 사용하여 관찰 또는 샘플 데이터를 평가할 수도 있습니다.
현재 연구 문헌에는 몇 가지 중요한 방향이 있습니다. 이 기사에서는 주로 복잡한 분포의 샘플링 프로세스를 모델링하고 프로세스를 적대적인 방식으로 학습하는 GAN을 포함하여 높은 수준에서 간략하게 소개합니다. "우도 기반" 방법이라고도 하는 생성 모델은 관찰된 데이터 샘플에 높은 가능성을 할당할 수 있으며 일반적으로 자동 회귀, 정규화된 흐름 및 VAE를 포함합니다. 에너지 기반 모델링, 이 접근 방식에서는 분포가 임의의 유연한 에너지 함수로 학습된 다음 정규화됩니다. 점수 기반 생성 모델에서는 에너지 함수 자체를 모델링하는 방법을 학습하는 것이 아니라, 에너지 모델을 기반으로 한 점수를 신경망으로 학습합니다.
이 연구에서는 확산 모델을 탐색하고 검토하며, 논문에 표시된 것처럼 가능성 기반 해석과 점수 기반 해석이 있습니다.
Variational Diffusion Model
간단히 살펴보면 VDM(Variational Diffusion Model)은 세 가지 주요 제한 사항(또는 가정)을 갖는 Markov 계층적 변형으로 간주할 수 있으며 오토인코더(MHVAE)로 나누어지며, :
- 잠재 차원은 데이터 차원과 정확히 동일합니다.
- 각 시간 단계의 잠재 인코더 구조는 학습되지 않으며 선형 가우스 모델로 미리 정의됩니다. 즉, 이전 시간 단계의 출력을 중심으로 한 가우스 분포이며, 잠재 인코더의 가우스 매개변수는 시간에 따라 변하며, 그 과정에서 마지막 시간 단계 T에서의 잠재 분포는 준가우스 분포입니다.
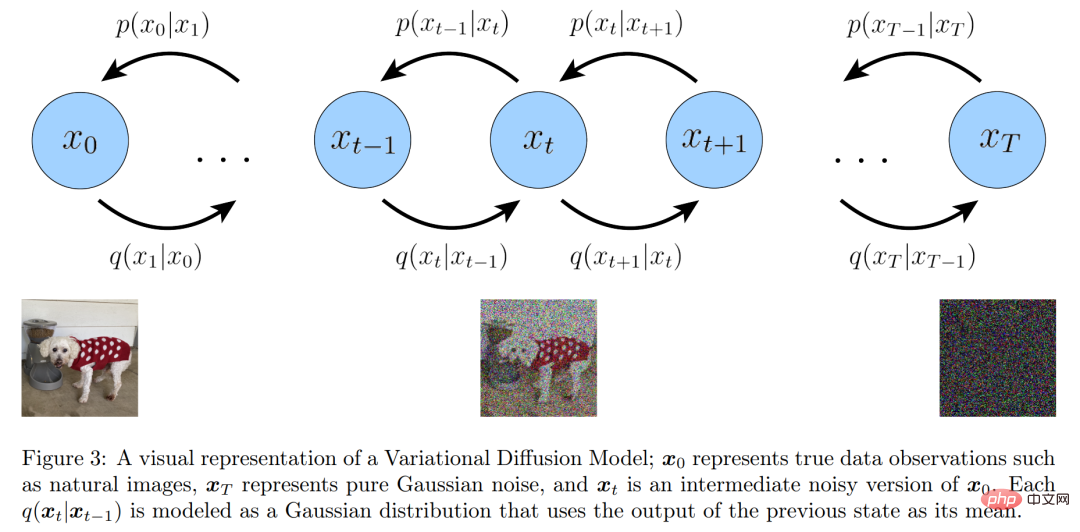변이 확산 모델의 시각적 표현
또한 연구원들은 표준 Markov 계층적 변이 자동 인코더의 계층적 변환 간의 관계를 명시적으로 유지합니다. 그들은 위의 세 가지 주요 가정의 의미를 하나씩 확장했습니다.
첫 번째 가정부터 시작해 기호의 오용으로 인해 실제 데이터 샘플과 잠재 변수는 이제 x_t로 표현될 수 있습니다. 여기서 t=0은 실제 샘플 데이터를 나타내고 t ∈ [1, T]는 해당 잠재 변수 , 그 계층 구조는 t로 색인화됩니다. VDM 사후는 MHVAE 사후와 동일하지만 이제 다음과 같이 다시 작성할 수 있습니다.
두 번째 가정으로부터 인코더의 각 잠재 변수의 분포는 이전 레이어 잠재 변수는 중심 가우스 분포입니다. MHVAE와 달리 각 시간 단계의 인코더 구조는 학습되지 않고 선형 가우스 모델로 고정되어 있으며 평균 및 표준 편차를 하이퍼파라미터로 미리 설정하거나 매개변수로 학습할 수 있습니다. 수학적으로 인코더 변환은 다음과 같이 표현됩니다.
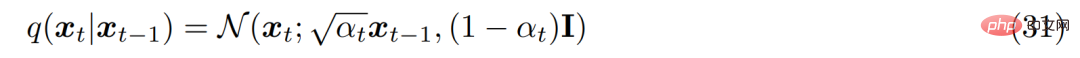세 번째 가설의 경우 α_t는 고정되거나 학습 가능한 일정에 따라 시간이 지남에 따라 진화하므로 최종 잠재 변수 p(x_T)의 분포는 다음과 같습니다. 표준 가우스 분포. 그러면 MHVAE의 공동 분포가 업데이트될 수 있으며 VDM의 공동 분포는 다음과 같이 작성될 수 있습니다.
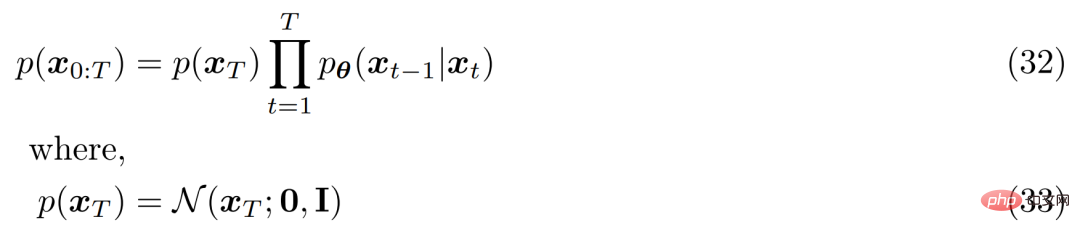요약하면, 이 일련의 가정은 시간이 지남에 따라 진화하는 이미지의 안정적인 노이즈를 설명합니다. 연구원들은 결국 가우스 잡음과 동일해질 때까지 가우스 잡음을 추가하여 이미지를 점진적으로 손상시켰습니다.
모든 HVACE와 마찬가지로 VDM은 다음과 같이 도출할 수 있는 ELBO(Evidence Lower Bound)를 최대화하여 최적화할 수 있습니다.
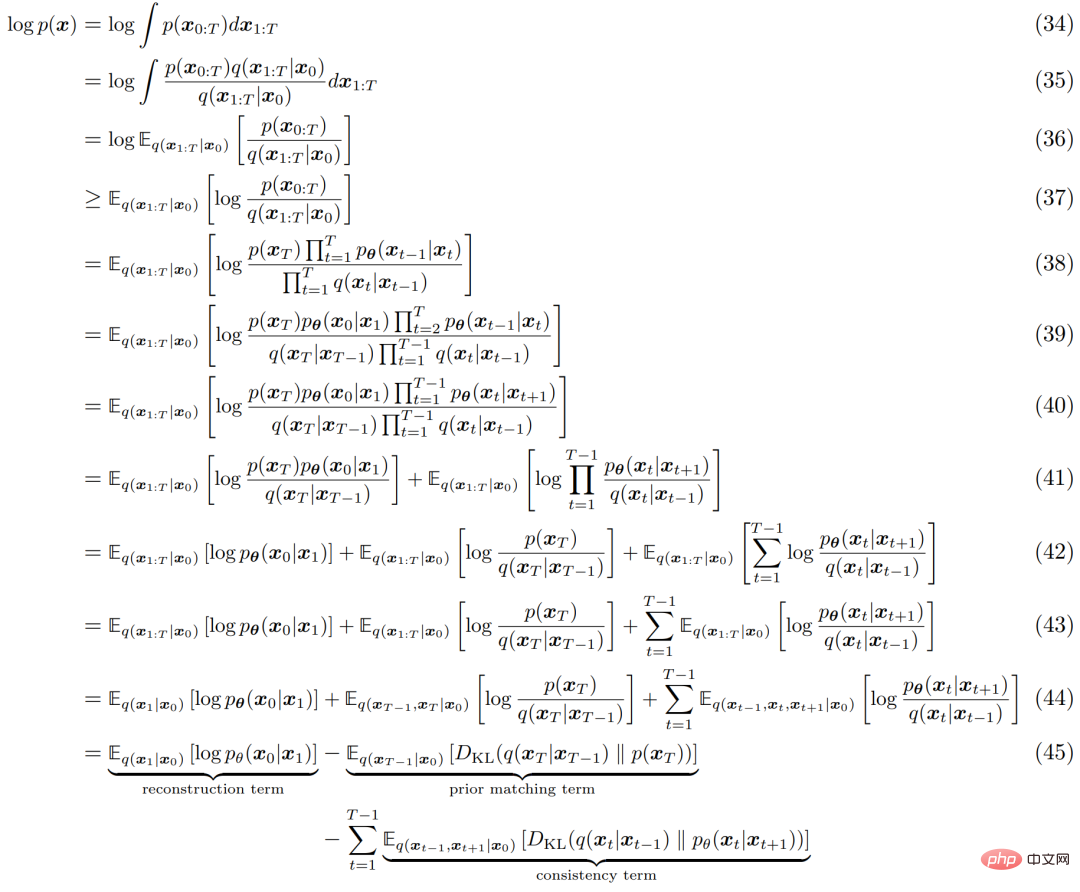ELBO의 해석 프로세스는 아래 그림 4에 나와 있습니다. . :
세 가지 등가 해석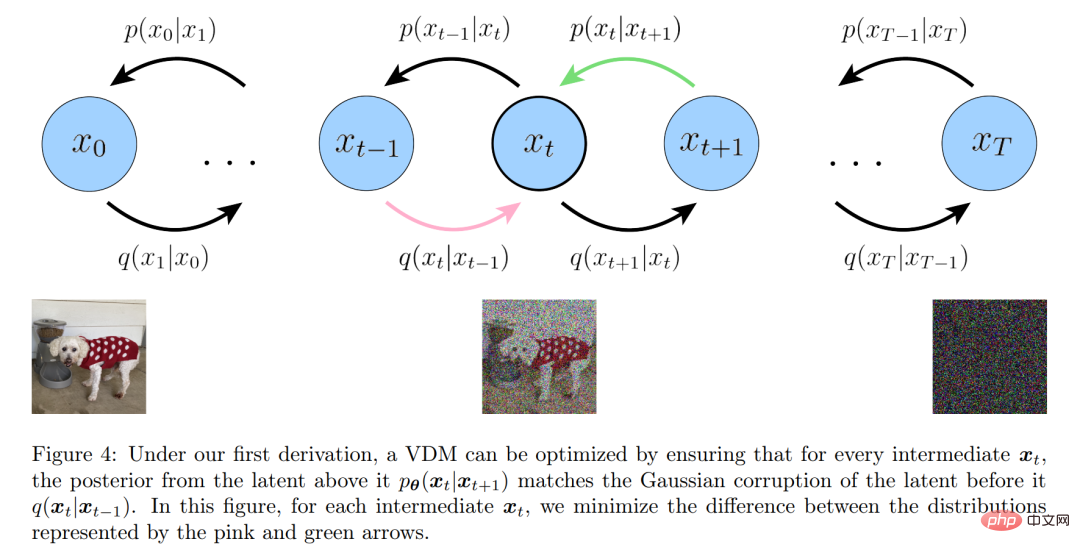
먼저, Heavy 매개변수화 기술을 사용할 수 있습니다. q(x_t|x_0)의 형태를 유도할 때 방정식 69는 다음과 같이 재배열될 수 있습니다.
이를 이전에 도출된 실제 잡음 제거 변환 평균 µ_q(x_t, x_0)에 가져오면 다음과 같이 다시 도출할 수 있습니다.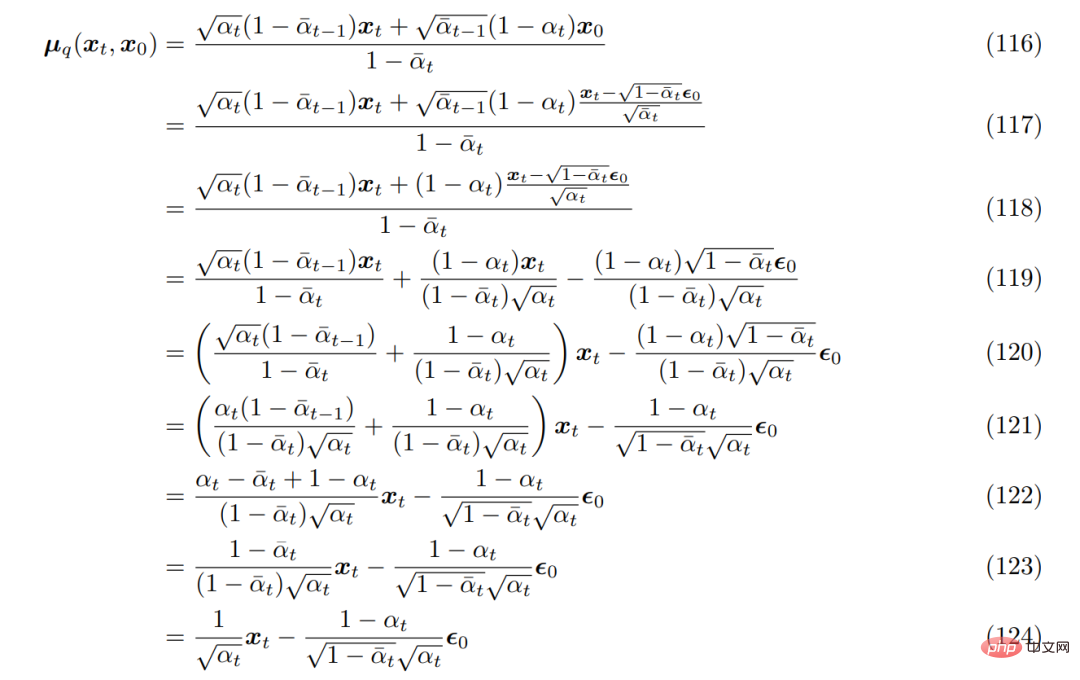 
따라서 대략적인 잡음 제거 변환 평균 µ_θ(x_t, t)는 다음과 같이 설정할 수 있습니다. :
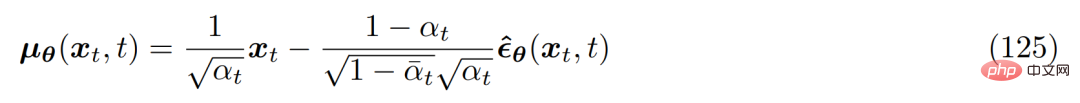
해당 최적화 문제는 다음과 같습니다.
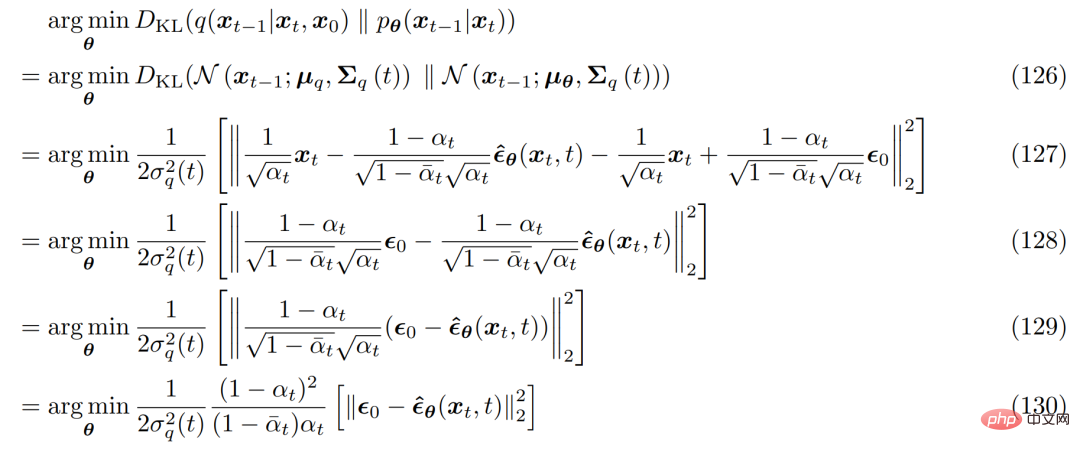
변이 확산 모델의 세 가지 일반적인 해석을 도출하려면 Tweedie 공식으로 전환해야 합니다. 이는 표본이 주어졌을 때 표본의 최대 우도 추정치(경험적 평균이라고도 함)에 추정 점수와 관련된 일부 수정 항을 더하여 지수족 분포의 실제 평균을 추정할 수 있다는 것을 의미합니다.
수학적으로 말하면 가우스 변수 z ∼ N(z; µ_z, Σ_z)에 대해 Tweedie 공식은 다음과 같이 표현됩니다. , 변형 확산 모델은 점수 함수 ∇ log p(x_t)를 예측하기 위해 신경망 s_θ(x_t, t)를 최적화함으로써 간단히 학습될 수 있습니다. 그러나 파생의 채점 용어는 Tweedie 공식을 적용한 것에서 비롯됩니다. 이는 점수 함수가 정확히 무엇인지 또는 모델링할 가치가 있는 이유에 대한 좋은 직관이나 통찰력을 반드시 제공하지는 않습니다.
다행히도 우리는 또 다른 유형의 생성 모델, 즉 점수 기반 생성 모델의 도움으로 이러한 직관을 얻을 수 있습니다. 연구원들은 실제로 이전에 파생된 VDM 공식이 동등한 분수 기반 생성 모델링 공식을 갖고 있어 두 해석 간에 유연하게 전환할 수 있음을 입증했습니다.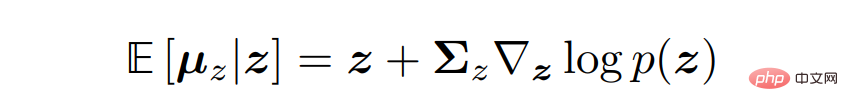 
점수 함수를 최적화하는 것이 왜 타당한지 이해하기 위해 연구원들은 에너지 기반 모델을 다시 검토했습니다. 임의의 유연한 확률 분포는 다음과 같이 작성할 수 있습니다.
정규화 상수를 계산하거나 모델링하는 것을 피하는 한 가지 방법은 신경망 s_θ(x)를 사용하여 분포 p( x) 함수 ∇ log p(x). 방정식 152의 양변은 로그 미분될 수 있음이 관찰됩니다.
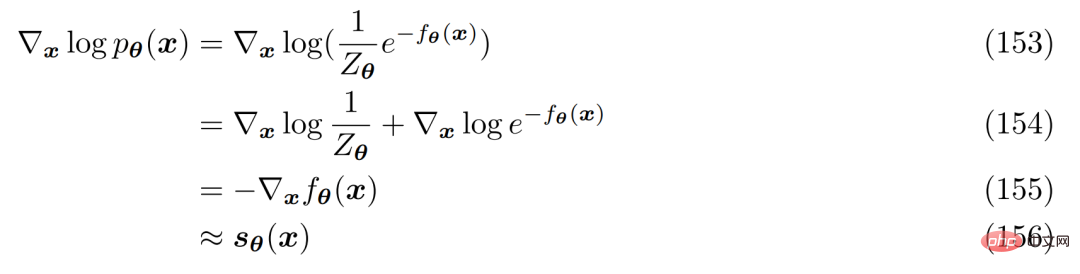
자세한 내용은 원문을 참고해주세요.
위 내용은 확산 모델 뒤에 숨은 수학은 소화하기 너무 어렵나요? Google은 통일된 관점으로 이를 명확하게 설명합니다.의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!