Java 시퀀스 목록 및 연결 목록에 대한 자세한 설명과 예제
- WBOY앞으로
- 2022-11-25 16:51:501424검색
이 기사에서는 java에 대한 관련 지식을 제공하며, 시퀀스 테이블과 연결 목록에 대한 관련 내용을 주로 소개합니다. 시퀀스 테이블은 연속된 물리적 주소를 갖는 저장 단위를 사용하여 데이터 요소를 순차적으로 저장하는 배열입니다. 선형 구조를 살펴보는 것이 모든 사람에게 도움이 되기를 바랍니다.

추천 학습: "java 비디오 튜토리얼"
1. 선형 목록
선형 목록은 동일한 특성을 가진 n개의 데이터 요소로 구성된 유한 시퀀스입니다. 선형 테이블은 실제로 널리 사용되는 데이터 구조입니다. 일반적인 선형 테이블: 시퀀스 목록, 연결 목록, 스택, 큐, 문자열...
선형 테이블은 논리적으로 선형 구조, 즉 연속적인 직선입니다. 그러나 물리적 구조가 반드시 연속적인 것은 아닙니다. 선형 테이블이 물리적으로 저장되는 경우 일반적으로 배열 및 연결된 구조의 형태로 저장됩니다.
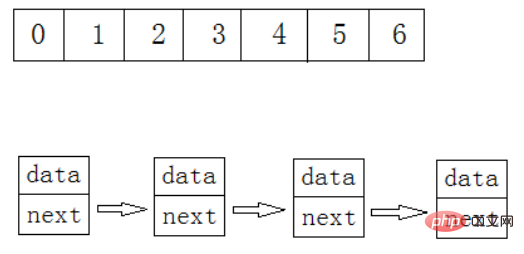
2. 시퀀스 목록
은 실제로 배열 입니다. [추가, 삭제, 확인 및 수정] 그런데 왜 아직도 시퀀스 테이블을 직접 배열로 작성하시나요? 다릅니다. 클래스에 작성하면 나중에 객체 지향이 될 수 있습니다.
2.1 개념 및 구조
시퀀스 테이블은 연속된 물리적 주소를 갖는 저장 단위를 사용하여 데이터 요소를 순차적으로 저장하는 선형 구조입니다. 일반적으로 배열 저장 장치가 사용됩니다. 어레이의 데이터 추가, 삭제, 확인 및 수정을 완료합니다.
시퀀스 테이블은 일반적으로 다음과 같이 나눌 수 있습니다.
- 정적 시퀀스 테이블: 고정 길이 배열 저장소를 사용합니다.
- 동적 시퀀스 테이블: 동적으로 열린 배열 저장소를 사용합니다.
정적 시퀀스 테이블은 얼마나 많은 데이터를 저장해야 하는지 알고 있는 시나리오에 적합합니다.
정적 시퀀스 테이블의 고정 길이 배열로 인해 N이 너무 많은 공간이 낭비됩니다. 공간이 너무 적으면 충분하지 않습니다.
동적 시퀀스 테이블은 더 유연하고 필요에 따라 동적으로 공간을 할당할 수 있습니다.
2.2 인터페이스 구현
다음은 동적 시퀀스 테이블을 구현해 보겠습니다.

여기서 하나씩 분해합니다. Out:
public class MyArrayList {
public int[] elem;
public int usedSize;//有效的数据个数
public MyArrayList() {
this.elem = new int[10];
}
// 打印顺序表public void display() {
}
System.out.println();}// 获取顺序表长度public int size() {
return 0;}// 在 pos 位置新增元素public void add(int pos, int data) {}// 判定是否包含某个元素public boolean contains(int toFind) {
return true;}// 查找某个元素对应的位置public int search(int toFind) {
return -1;}// 获取 pos 位置的元素public int getPos(int pos) {
return -1;}// 给 pos 位置的元素设为 valuepublic void setPos(int pos, int value) {}//删除第一次出现的关键字keypublic void remove(int toRemove) {}// 清空顺序表public void clear() {}}
이것이 시퀀스 테이블의 기본 구조입니다. 시퀀스 테이블의 기능을 하나씩 분석해 보겠습니다.
데이터 테이블 인쇄:
public void display() {
for (int i = 0; i < this.usedSize; i++) {
System.out.print(this.elem[i] + " ");
}
System.out.println();}시퀀스 테이블의 길이 가져오기:
public int size() {
return this.usedSize;}pos 위치에 요소 추가:
public void add(int pos, int data) {
if(pos < 0 || pos > this.usedSize) {
System.out.println("pos 位置不合法");
return;
}
if(isFull()){
this.elem = Arrays.copyOf(this.elem,2*this.elem.length);
}
for (int i = this.usedSize-1; i >= pos; i--) {
this.elem[i + 1] = this.elem[i];
}
this.elem[pos] = data;
this.usedSize++;}//判断数组元素是否等于有效数据个数public boolean isFull() {
return this.usedSize == this.elem.length;}
특정 요소가 있는지 판단 포함됨:
public boolean contains(int toFind) {
for (int i = 0; i < this.usedSize; i++) {
if (this.elem[i] == toFind) {
return true;
}
}
return false;} 요소에 해당하는 위치 찾기:
public int search(int toFind) {
for (int i = 0; i < this.usedSize; i++) {
if (this.elem[i] == toFind) {
return i;
}
}
return -1;}pos 위치에서 요소 가져오기:
public int getPos(int pos) {
if (pos < 0 || pos >= this.usedSize){
System.out.println("pos 位置不合法");
return -1;//所以 这里说明一下,业务上的处理,这里不考虑
}
if(isEmpty()) {
System.out.println("顺序表为空!");
return -1;
}
return this.elem[pos];}//判断数组链表是否为空public boolean isEmpty() {
return this.usedSize == 0;}
pos 위치의 요소를 값으로 설정:
public void setPos(int pos, int value) {
if(pos < 0 || pos >= this.usedSize) {
System.out.println("pos 位置不合法");
return;
}
if(isEmpty()) {
System.out.println("顺序表为空!");
return;
}
this.elem[pos] = value;}//判断数组链表是否为空public boolean isEmpty() {
return this.usedSize == 0;}
키워드 키의 첫 번째 항목 삭제:
public void remove(int toRemove) {
if(isEmpty()) {
System.out.println("顺序表为空!");
return;
}
int index = search(toRemove);//index记录删除元素的位置
if(index == -1) {
System.out.println("没有你要删除的数字!");
}
for (int i = index; i < this.usedSize - 1; i++) {
this.elem[i] = this.elem[i + 1];
}
this.usedSize--;
//this.elem[usedSize] = null;引用数组必须这样做才可以删除} 시퀀스 목록 지우기:
public void clear() {
this.usedSize = 0;}2.3 시퀀스 테이블에 대한 문제와 생각
시퀀스 테이블의 중간/머리 부분에 삽입 및 삭제, 시간 복잡도는 O(N)
증가 용량을 늘리려면 새 공간을 신청하고 데이터를 복사해야 합니다. 소비가 많을 겁니다.
용량 확장은 일반적으로 2배로 늘어나는데, 어느 정도 낭비되는 공간이 있을 수밖에 없습니다. 예를 들어 현재 용량이 100인데 꽉 차면 200으로 늘어난다. 계속해서 5개의 데이터를 삽입하고 나중에는 어떤 데이터도 삽입하지 않으므로 95개의 데이터 공간이 낭비된다.
생각하기: 위의 문제를 해결하는 방법은 무엇입니까? 링크드 리스트의 구조는 아래에서 살펴보도록 하겠습니다.
3. 연결 목록
3.1 연결 목록의 개념과 구조
연결 목록은 비연속적물리적 저장 구조입니다. 데이터 요소의 논리적 순서는 참조를 통해 이루어집니다. 연결리스트에서는 링크가 순서대로 구현됩니다.
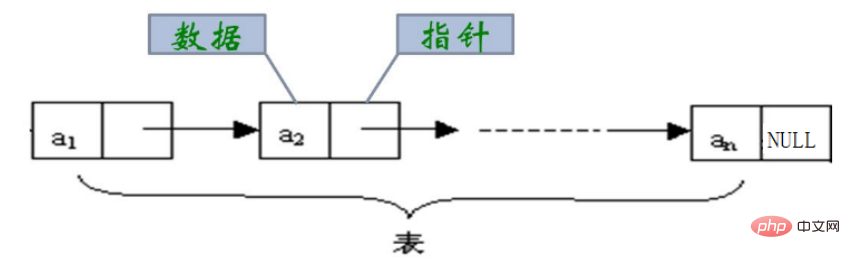
- 단방향 연결 목록
- 이중 연결 목록
- 원형 연결 목록
- 양방향 순환 연결 리스트
- 8가지 유형은 다음과 같습니다. 단방향 선행 루프
단방향 선행 루프
단방향 선행 비루프
- 단방향 선행 비순환 -loop
- 양방향 선행 루프
양방향 선행 없음 루프
양방향 선행 비루프
- 양방향 선행 비루프
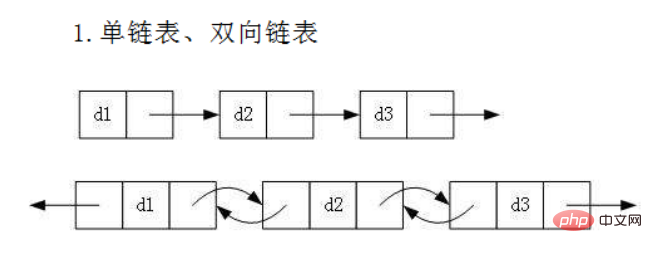
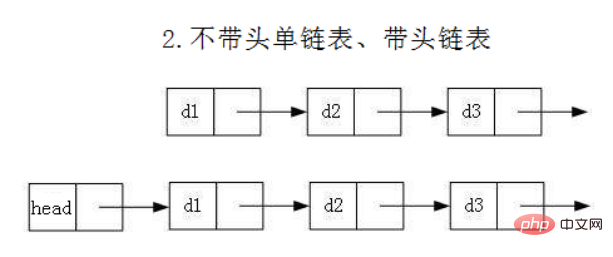
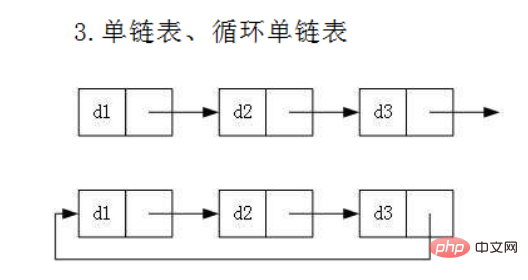
虽然有这么多的链表的结构,但是我们重点掌握两种:
- 无头单向非循环链表:结构简单,一般不会单独用来存数据。实际中更多是作为其他数据结构的子结构,如哈希桶、图的邻接表等等。另外这种结构在笔试面试中出现很多。
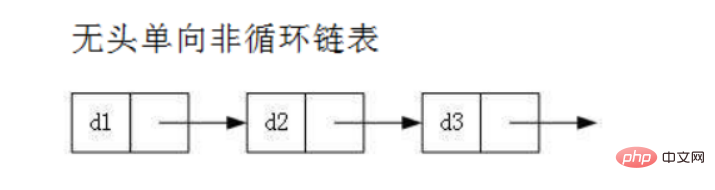
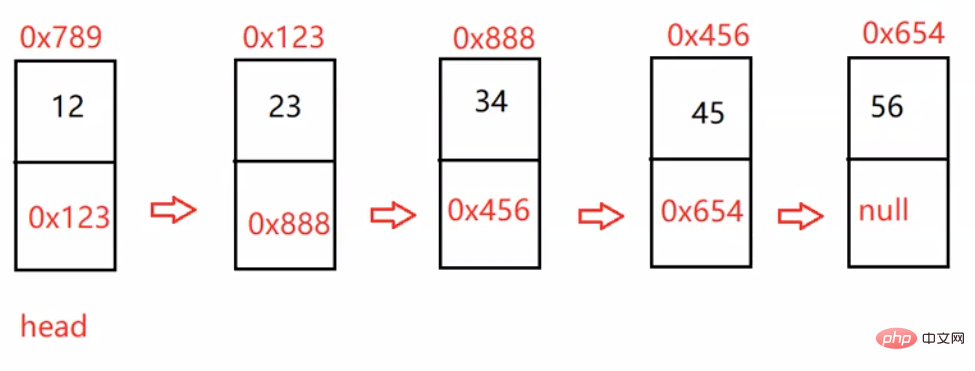
head:里面存储的就是第一个节点(头节点)的地址
head.next:存储的就是下一个节点的地址
尾结点:它的next域是一个null
- 无头双向链表:在Java的集合框架库中LinkedList底层实现就是无头双向循环链表。
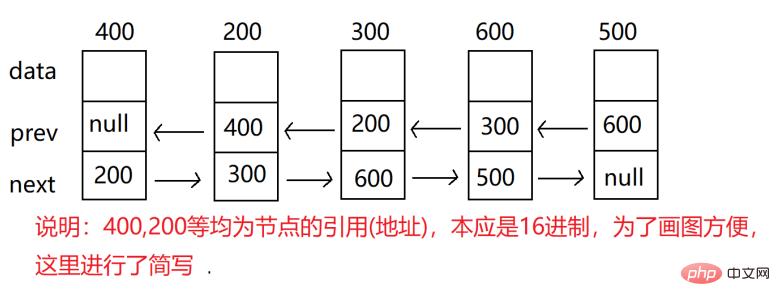
最上面的数字是我们每一个数值自身的地址。
prev:指向前一个元素地址
next:下一个节点地址
data:数据
3.2 链表的实现
3.2.1无头单向非循环链表的实现
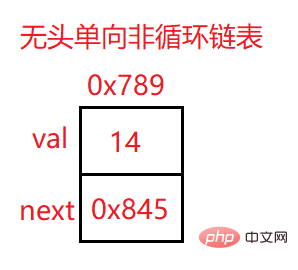
上面地址为改结点元素的地址
val:数据域
next:下一个结点的地址
head:里面存储的就是第一个结点(头结点)的地址
head.next:存储的就是下一个结点的地址
无头单向非循环链表实现:
class ListNode { public int val; public ListNode next;//ListNode储存的是结点类型 public ListNode (int val) { this.val = val; }}public class MyLinkedList { public ListNode head;//链表的头引用 public void creatList() { ListNode listNode1 = new ListNode(12); ListNode listNode2 = new ListNode(23); ListNode listNode3 = new ListNode(34); ListNode listNode4 = new ListNode(45); ListNode listNode5 = new ListNode(56); listNode1.next = listNode2; listNode2.next = listNode3; listNode3.next = listNode4; listNode4.next = listNode5; this.head = listNode1; } //查找是否包含关键字key是否在单链表当中 public boolean contains(int key) { return true; } //得到单链表的长度 public int size(){ return -1; } //头插法 public void addFirst(int data) { } //尾插法 public void addLast(int data) { } //任意位置插入,第一个数据节点为0号下标 public boolean addIndex(int index,int data) { return true; } //删除第一次出现关键字为key的节点 public void remove(int key) { } //删除所有值为key的节点 public ListNode removeAllKey(int key) { } //打印链表中的所有元素 public void display() { } //清除链表中所有元素 public void clear() { }}上面是我们链表的初步结构(未给功能赋相关代码,大家可以复制他们到自己的idea中进行练习,答案在下文中) 这里我们将他们一个一个拿出来实现 并实现!
打印链表中所有元素:
public void display() { ListNode cur = this.head; while(cur != null) { System.out.print(cur.val + " "); cur = cur.next; } System.out.println();}查找是否包含关键字key是否在单链表当中:
public boolean contains(int key) { ListNode cur = this.head; while (cur != null) { if (cur.val == key) { return true; } cur = cur.next; } return false;}得到单链表的长度:
public int size(){ int count = 0; ListNode cur = this.head; while (cur != null) { count++; cur = cur.next; } return count;}头插法(一定要记住 绑定位置时一定要先绑定后面的数据 避免后面数据丢失):
public void addFirst(int data) { ListNode node = new ListNode(data); node.next = this.head; this.head = node; /*if (this.head == null) { this.head = node; } else { node.next = this.head; this.head = node; }*/}尾插法:
public void addLast(int data) { ListNode node = new ListNode(data); if (this.head == null) { this.head = node; } else { ListNode cur = this.head; while (cur.next != null) { cur = cur.next; } cur.next = node; }}任意位置插入,第一个数据结点为0号下标(插入到index后面一个位置):
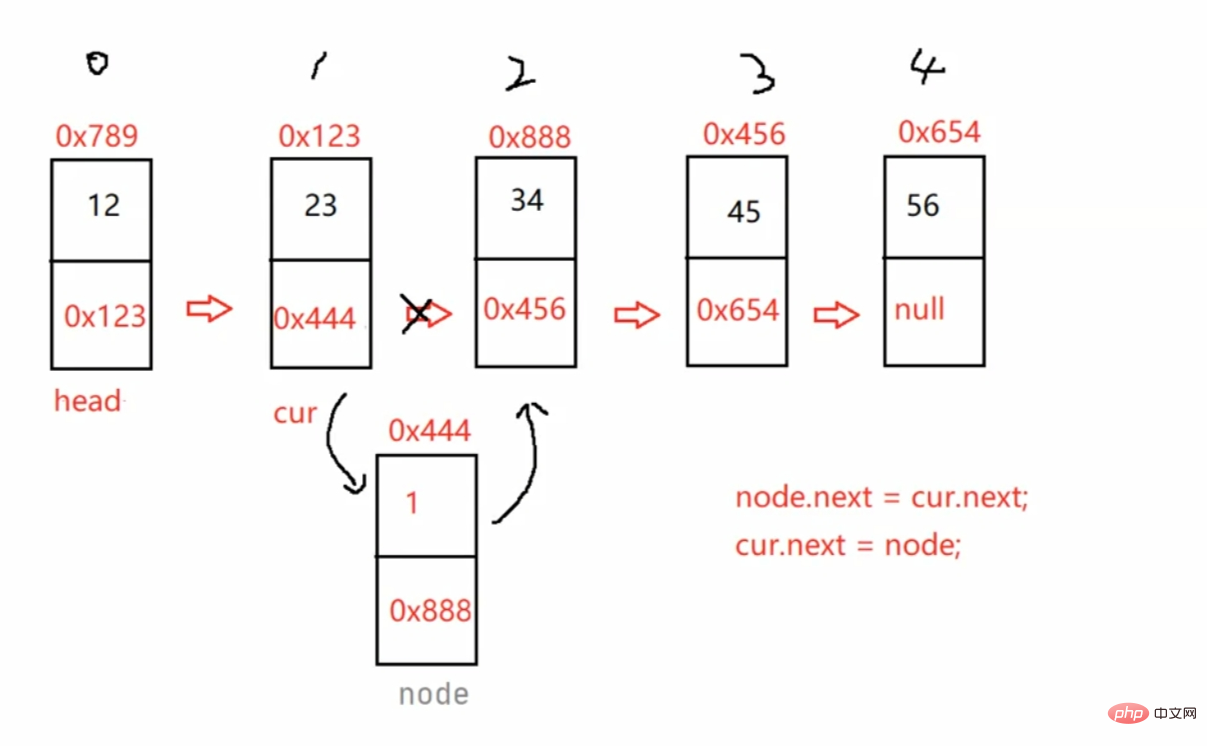
/** * 找到index - 1位置的节点的地址 * @param index * @return */public ListNode findIndex(int index) { ListNode cur = this.head; while (index - 1 != 0) { cur = cur.next; index--; } return cur;}//任意位置插入,第一个数据节点为0号下标public void addIndex(int index,int data) { if(index < 0 || index > size()) { System.out.println("index 位置不合法!"); return; } if(index == 0) { addFirst(data); return; } if(index == size()) { addLast(data); return; } ListNode cur = findIndex(index); ListNode node = new ListNode(data); node.next = cur.next; cur.next = node;}注意:单向链表找cur时要-1,但双向链表不用 直接返回cur就好
删除第一次出现关键字为key的结点:
/** * 找到 要删除的关键字key的节点 * @param key * @return */public ListNode searchPerv(int key) { ListNode cur = this.head; while(cur.next != null) { if(cur.next.val == key) { return cur; } cur = cur.next; } return null;}//删除第一次出现关键字为key的节点public void remove(int key) { if(this.head == null) { System.out.println("单链表为空"); return; } if(this.head.val == key) { this.head = this.head.next; return; } ListNode cur = searchPerv(key); if(cur == null) { System.out.println("没有你要删除的节点"); return; } ListNode del = cur.next; cur.next = del.next;}删除所有值为key的结点:
public ListNode removeAllKey(int key) { if(this.head == null) { return null; } ListNode prev = this.head; ListNode cur = this.head.next; while(cur != null) { if(cur.val == key) { prev.next = cur.next; cur = cur.next; } else { prev = cur; cur = cur.next; } } //最后处理头 if(this.head.val == key) { this.head = this.head.next; } return this.head;}清空链表中所有元素:
public void clear() { while (this.head != null) { ListNode curNext = head.next; head.next = null; head.prev = null; head = curNext; } last = null;}3.2.2无头双向非循环链表实现:
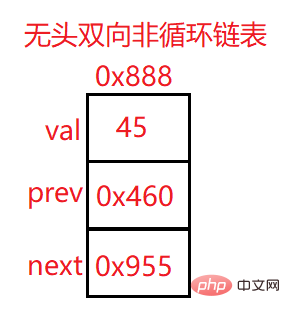
上面的地址0x888为该结点的地址
val:数据域
prev:上一个结点地址
next:下一个结点地址
head:头结点 一般指向链表的第一个结点
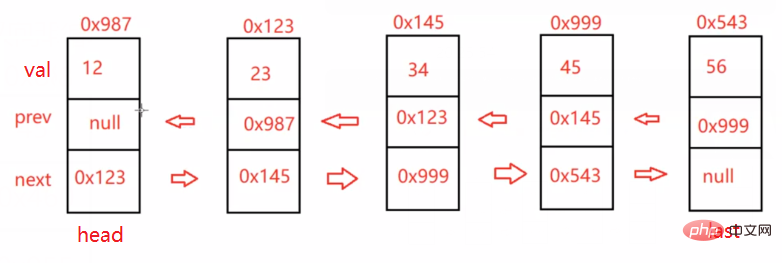
class ListNode { public int val; public ListNode prev; public ListNode next; public ListNode (int val) { this.val = val; }}public class MyLinkedList { public ListNode head;//指向双向链表的头结点 public ListNode last;//只想双向链表的尾结点 //打印链表 public void display() { } //得到单链表的长度 public int size() { return -1; } //查找是否包含关键字key是否在单链表当中 public boolean contains(int key) { return true; } //头插法 public void addFirst(int data) { } //尾插法 public void addLast(int data) { } //删除第一次出现关键字为key的节点 public void remove(int key) { } //删除所有值为key的节点 public void removeAllKey(int key) { } //任意位置插入,第一个数据节点为0号下标 public boolean addIndex(int index,int data) { return true; } //清空链表 public void clear() { }}上面是我们链表的初步结构(未给功能赋相关代码,大家可以复制他们到自己的idea中进行练习,答案在下文中) 这里我们将他们一个一个拿出来实现 并实现!
打印链表:
public void display() { ListNode cur = this.head; while (cur != null) { System.out.print(cur.val + " "); cur = cur.next; } System.out.println();}得到单链表的长度:
public int size() { ListNode cur = this.head; int count = 0; while (cur != null) { count++; cur = cur.next; } return count;}查找是否包含关键字key是否在单链表当中:
public boolean contains(int key) { ListNode cur = this.head; while (cur != null) { if (cur.val == key) { return true; } cur = cur.next; } return false;}头插法:
public void addFirst(int data) { ListNode node = new ListNode(data); if (this.head == null) { this.head = node; this.last = node; } else { node.next = this.head; this.head.prev = node; this.head = node; }}尾插法:
public void addLast(int data) { ListNode node = new ListNode(data); if (this.head == null) { this.head = node; this.last = node; } else { ListNode lastPrev = this.last; this.last.next = node; this.last = this.last.next; this.last.prev = lastPrev; /** * 两种方法均可 * this.last.next = node; * node.prev = this.last; * this.last = node; */ }}注:第一种方法是先让last等于尾结点 再让他的前驱等于上一个地址 而第二种方法是先使插入的尾结点的前驱等于上一个地址 再使其等于尾结点
删除第一次出现关键字为key的结点:
public void remove(int key) { ListNode cur = this.head; while (cur != null) { if (cur.val == key) { if (cur == head) { head = head.next; if (head != null) { head.prev = null; } else { last = null; } } else if (cur == last) { last = last.prev; last.next = null; } else { cur.prev.next = cur.next; cur.next.prev = cur.prev; } return; } cur = cur.next; }}删除所有值为key的结点:
public void removeAllKey(int key) { ListNode cur = this.head; while (cur != null) { if (cur.val == key) { if (cur == head) { head = head.next; if (head != null) { head.prev = null; } else { last = null; } } else if (cur == last) { last = last.prev; last.next = null; } else { cur.prev.next = cur.next; cur.next.prev = cur.prev; } //return; } cur = cur.next; }}注:他和remove的区别就是删除完后是不是直接return返回,如果要删除所有的key值则不return,让cur继续往后面走。
任意位置插入,第一个数据节点为0号下标:
public void addIndex(int index,int data) { if (index < 0 || index > size()) { System.out.println("index 位置不合法"); } if (index == 0) { addFirst(data); return; } if (index == size()) { addLast(data); return; } ListNode cur = searchIndex(index); ListNode node = new ListNode(data); node.next = cur; cur.prev.next = node; node.prev = cur.prev; cur.prev = node;}public ListNode searchIndex(int index) { ListNode cur = this.head; while (index != 0) { cur = cur.next; index--; } return cur;}思路:先判断 在头位置就头插 在尾位置就尾插 在中间就改变四个位置的值。
注意:单向链表找cur时要-1,但双向链表不用 直接返回cur就好
清空链表:
public void clear() { while (this.head != null) { ListNode curNext = head.next; head.next = null; head.prev = null; head = curNext; } last = null;}3.3 链表面试题
3.3.1反转链表:
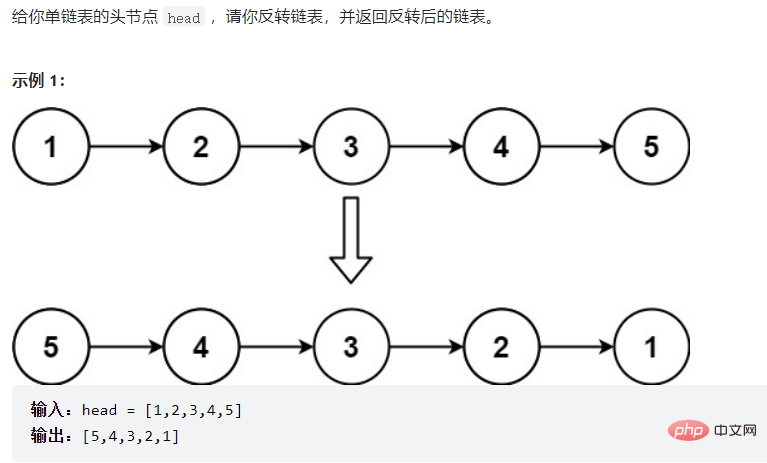

这里的
cur = this.head;
prev = null;
curNext = cur.next;
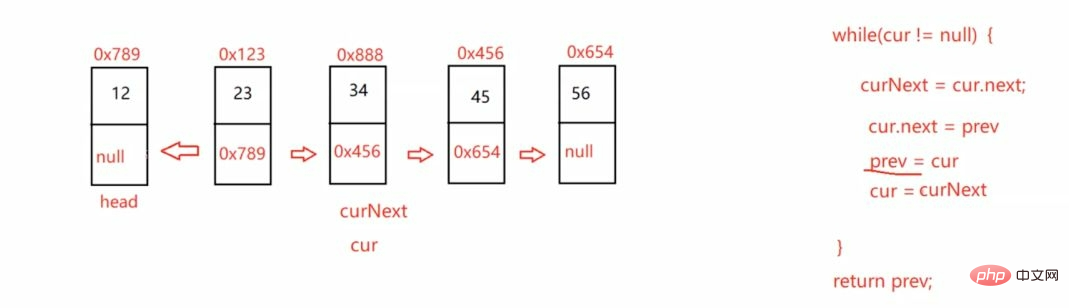
public ListNode reverseList() { if (this.head == null) { return null; } ListNode cur = this.head; ListNode prev = null; while (cur != null) { ListNode curNext = cur.next; cur.next = prev; prev = cur; cur = curNext; } return prev;}3.3.2找到链表的中间结点:


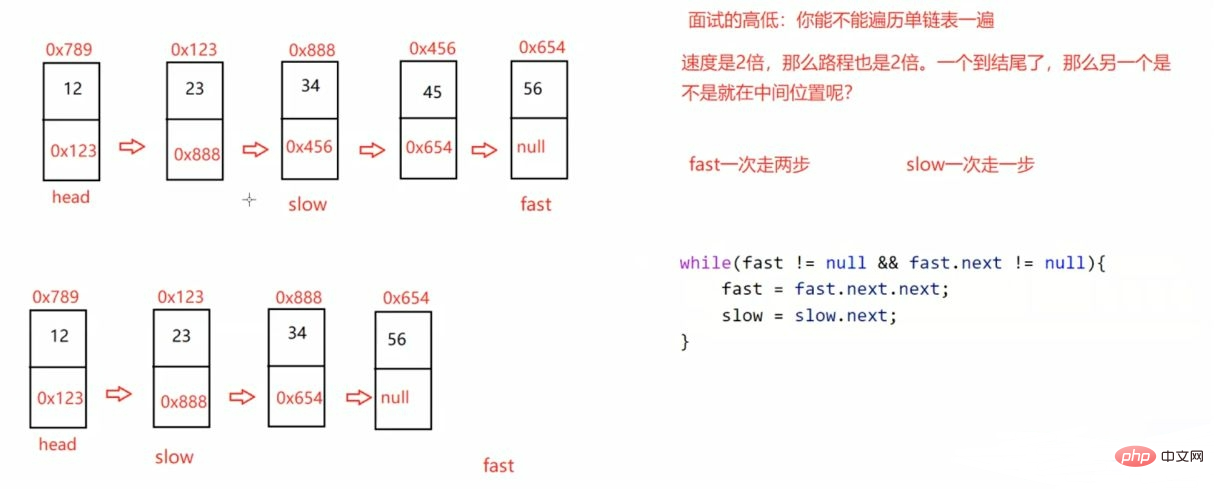
public ListNode middleNode() { if (head == null) { return null; } ListNode fast = head; ListNode slow = head; while (fast != null && fast.next != null) { fast = fast.next.next; if (fast == null) { return slow; } slow = slow.next; } return slow;}3.3.3输入一个链表 返回该链表中倒数第k个结点

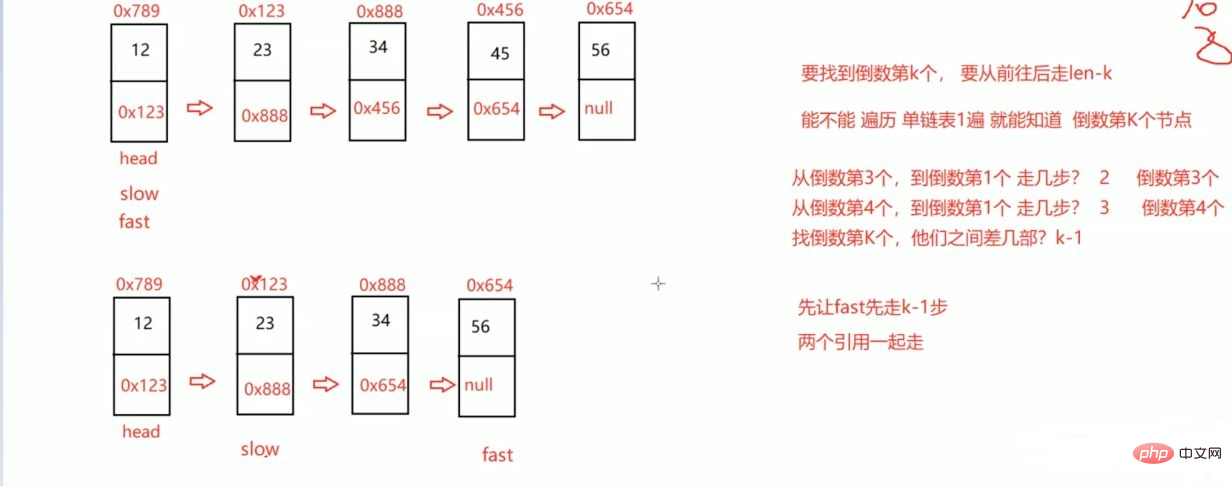
public ListNode findKthToTail(ListNode head,int k) { if (k <= 0 || head == null) { return null; } ListNode fast = head; ListNode slow = head; while (k - 1 != 0) { fast = fast.next; if (fast == null) { return null; } k--; } while (fast.next != null) { fast = fast.next; slow = slow.next; } return slow;}3.3.4合并两个链表 并变成有序的
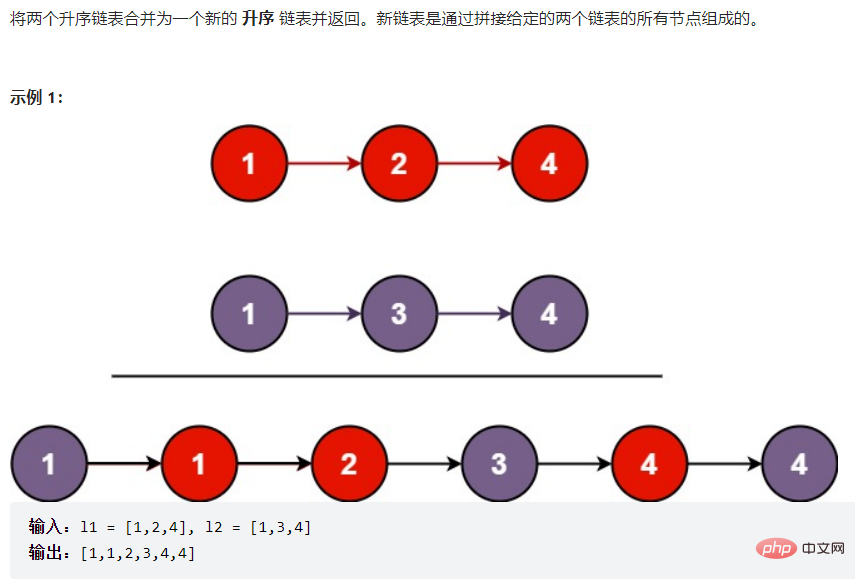

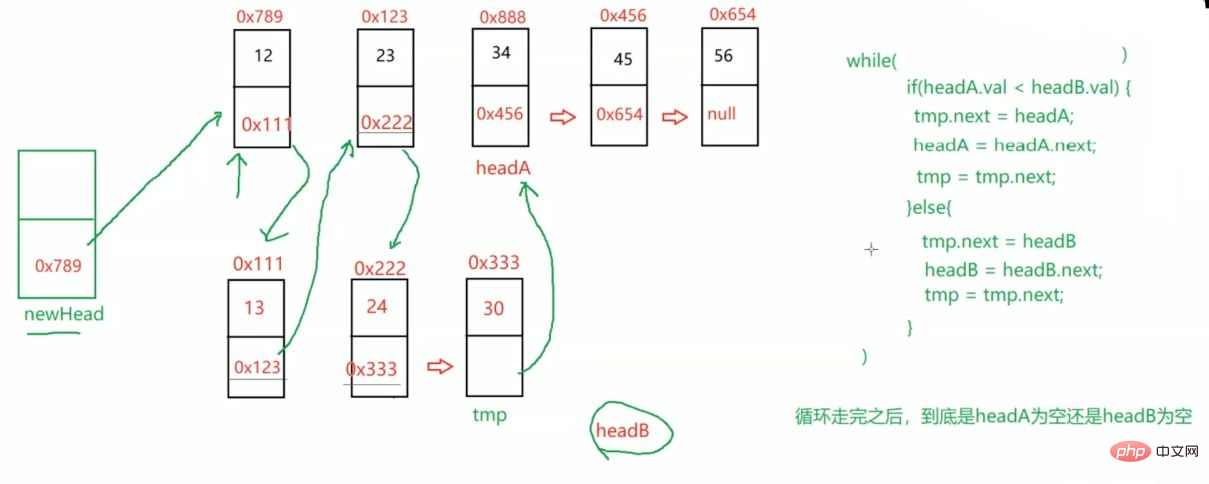
public static ListNode mergeTwoLists(ListNode headA,ListNode headB) { ListNode newHead = new ListNode(-1); ListNode tmp = newHead; while (headA != null && headB != null) { if(headA.val <headB.val) { tmp.next = headA; headA = headA.next; tmp = tmp.next; } else { tmp.next = headB; headB = headB.next; tmp = tmp.next; } } if (headA != null) { tmp.next = headA; } if (headB != null) { tmp.next = headB; } return newHead.next;}最后返回的是傀儡结点的下一个 即
newHead.next3.3.5 编写代码,以给定值x为基准将链表分割成两部分,所有小于x的结点排在大于或等于x的结点之前 。(即将所有小于x的放在x左边,大于x的放在x右边。且他们本身的排序不可以变)

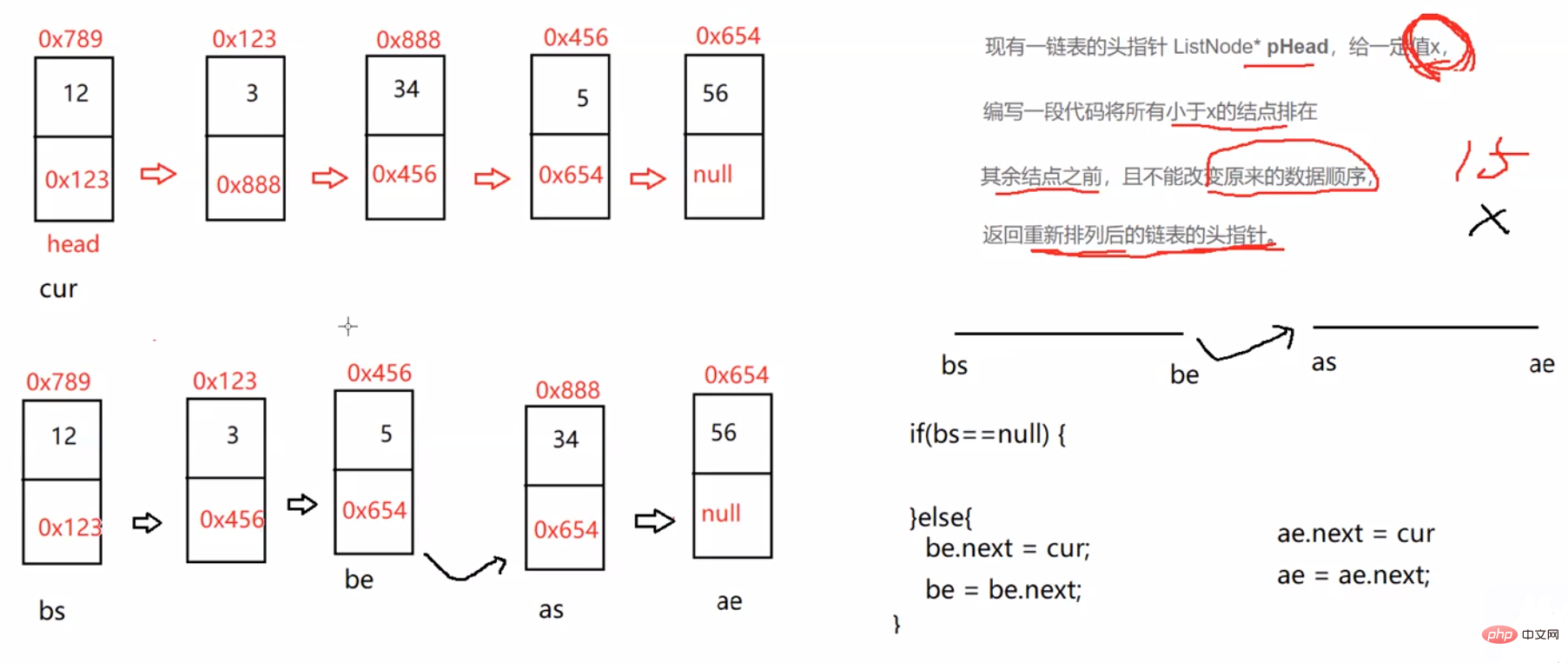
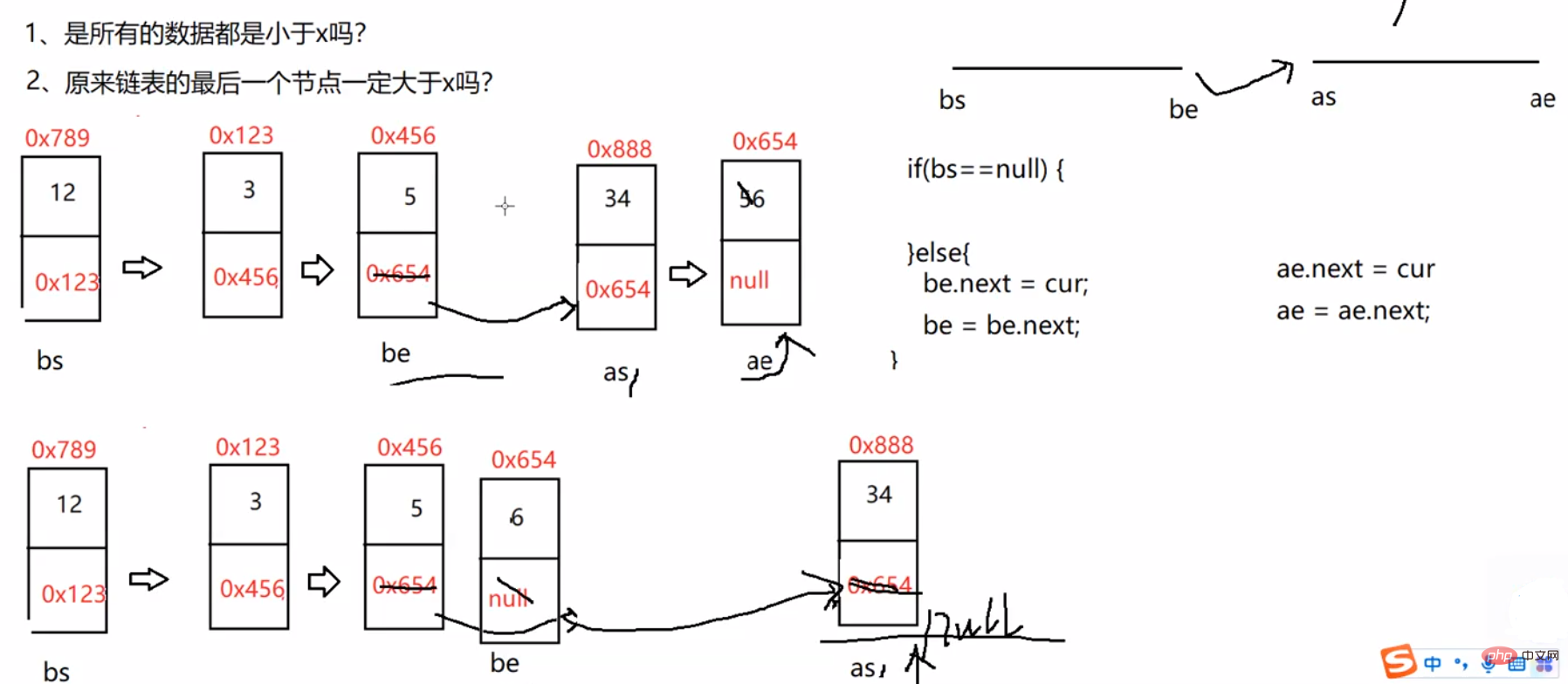
//按照x和链表中元素的大小来分割链表中的元素public ListNode partition(int x) { ListNode bs = null; ListNode be = null; ListNode as = null; ListNode ae = null; ListNode cur = head; while (cur != null) { if(cur.val < x){ //1、第一次 if (bs == null) { bs = cur; be = cur; } else { //2、不是第一次 be.next = cur; be = be.next; } } else { //1、第一次 if (as == null) { as = cur; as = cur; } else { //2、不是第一次 ae.next = cur; ae = ae.next; } } cur = cur.next; } //预防第1个段为空 if (bs == null) { return as; } be.next = as; //预防第2个段当中的数据,最后一个节点不是空的。 if (as != null) { ae.next = null; } return be;}3.3.6 在一个排序的链表中,存在重复的结点,请删除该链表中重复的结点,重复的结点不保留,返回链表头指针。(有序的链表中重复的结点一定是紧紧挨在一起的)
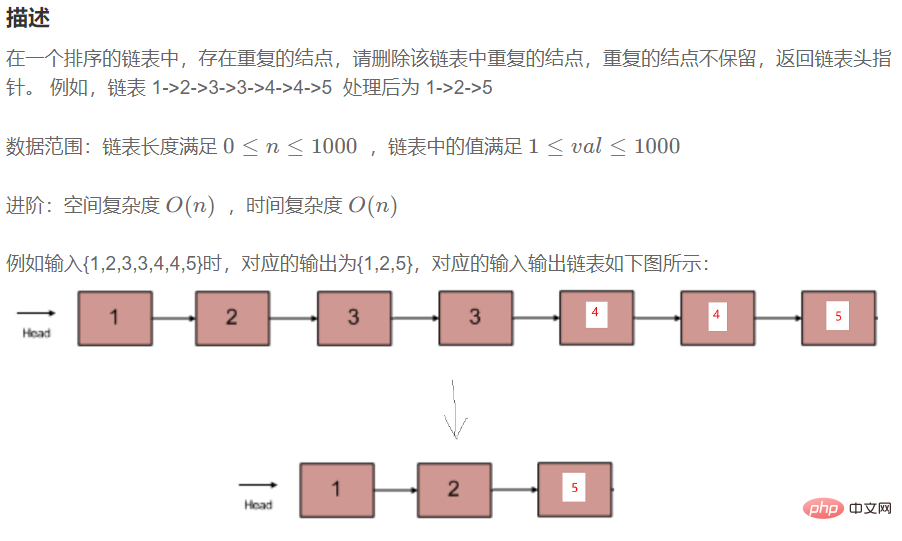

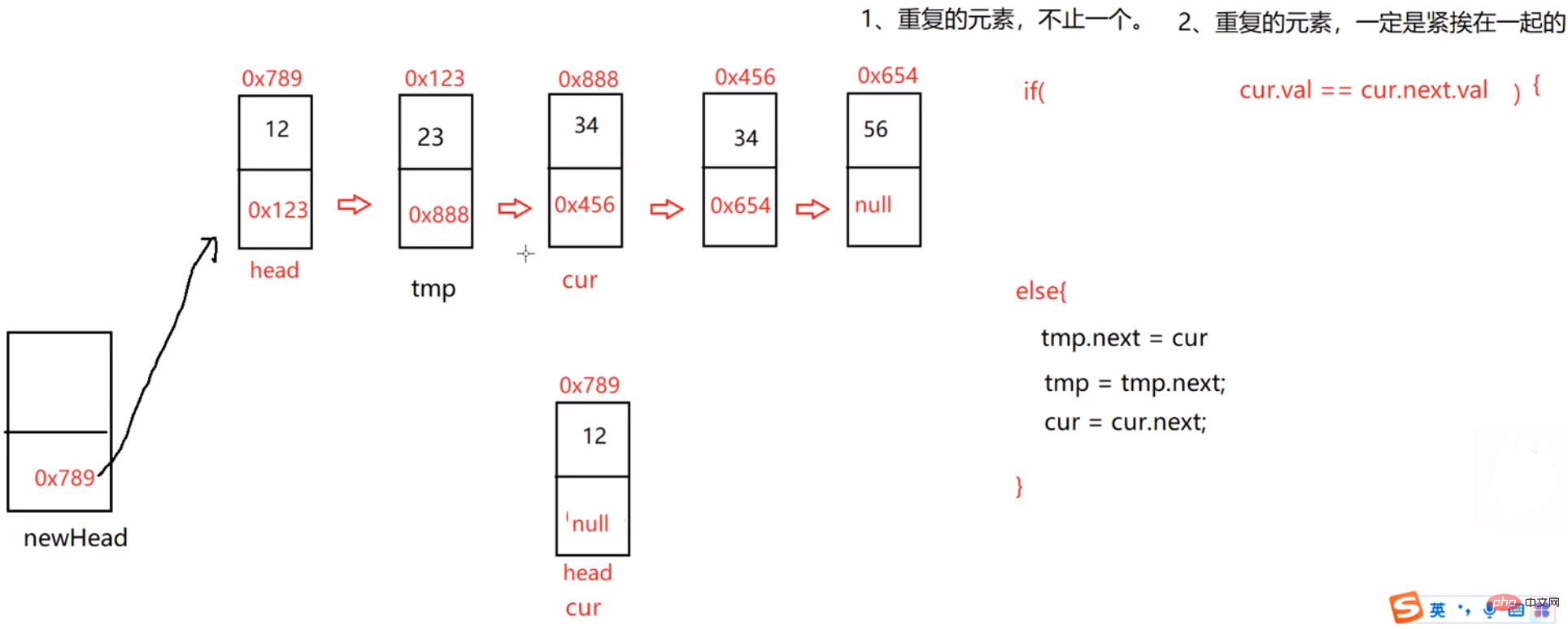
public ListNode deleteDuplication() { ListNode cur = head; ListNode newHead = new ListNode(-1); ListNode tmp = newHead; while (cur != null) { if (cur.next != null && cur.val == cur.next.val) { while (cur.next != null && cur.val == cur.next.val) { cur = cur.next; } //多走一步 cur = cur.next; } else { tmp.next = cur; tmp = tmp.next; cur = cur.next; } } //防止最后一个结点的值也是重复的 tmp.next = null; return newHead.next;}3.3.7 链表的回文结构。

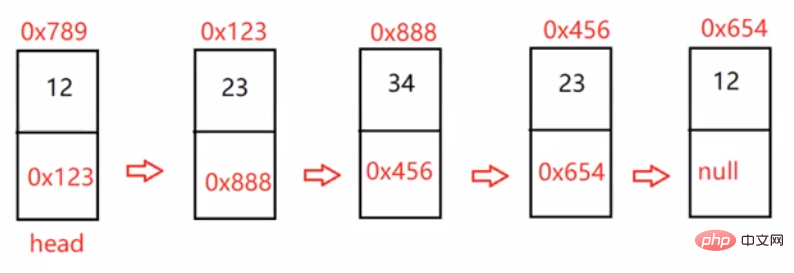
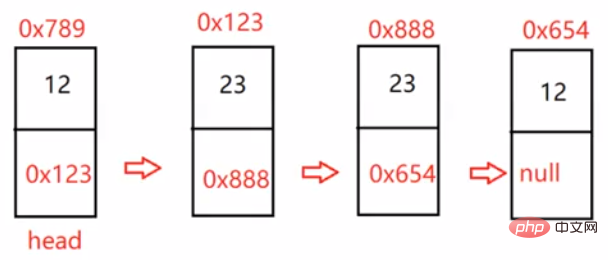
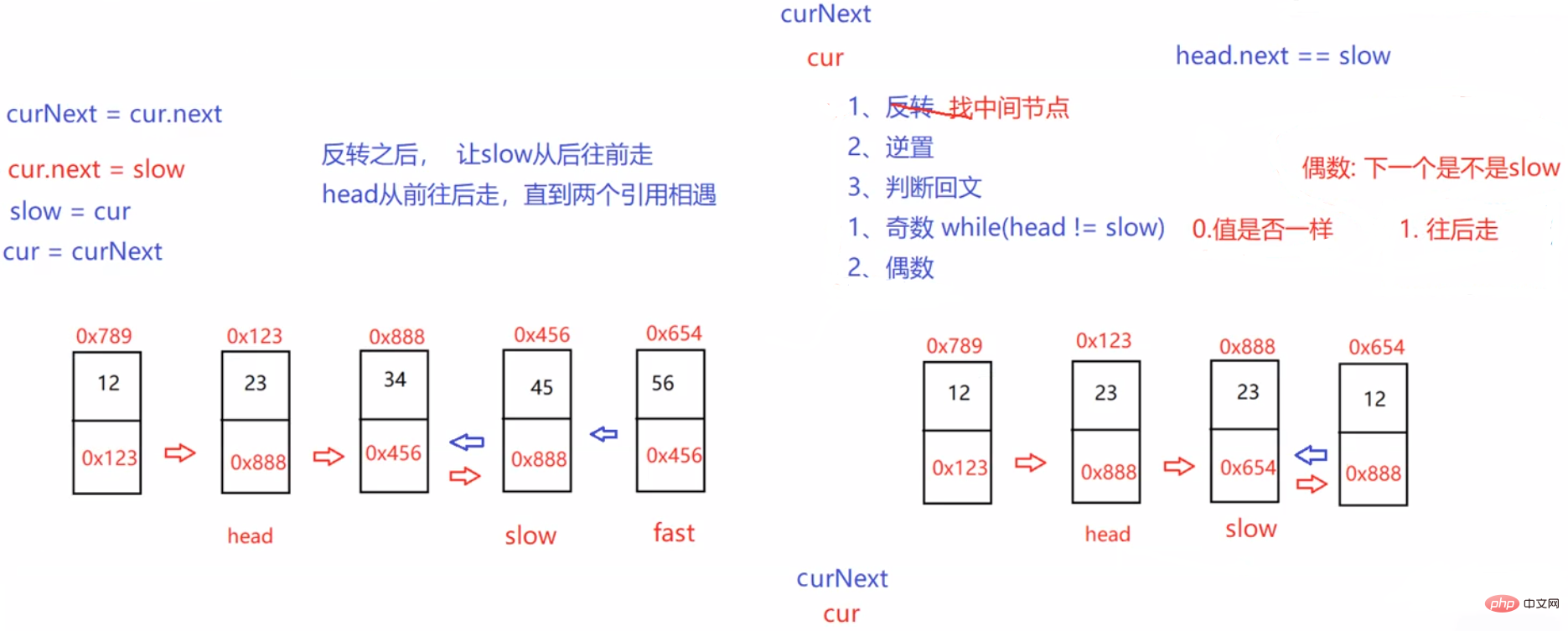
public boolean chkPalindrome(ListNode head) { if (head == null) { return true; } ListNode fast = head; ListNode slow = head; while (fast != null && fast.next != null) { fast = fast.next.next; slow = slow.next; } //slow走到了中间位置 ListNode cur = slow.next; while (cur != null) { ListNode curNext = cur.next; cur.next = slow; slow = cur; cur = curNext; } //反转完成 while (head != slow) { if(head.val != slow.val) { return false; } else { if (head.next == slow) { return true; } head = head.next; slow = slow.next; } return true; } return true;}3.3.8 输入两个链表,找出它们的第一个公共结点。
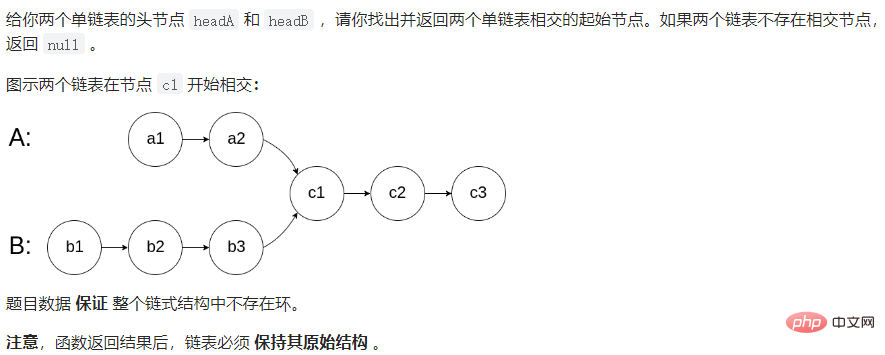
他是一个Y字形
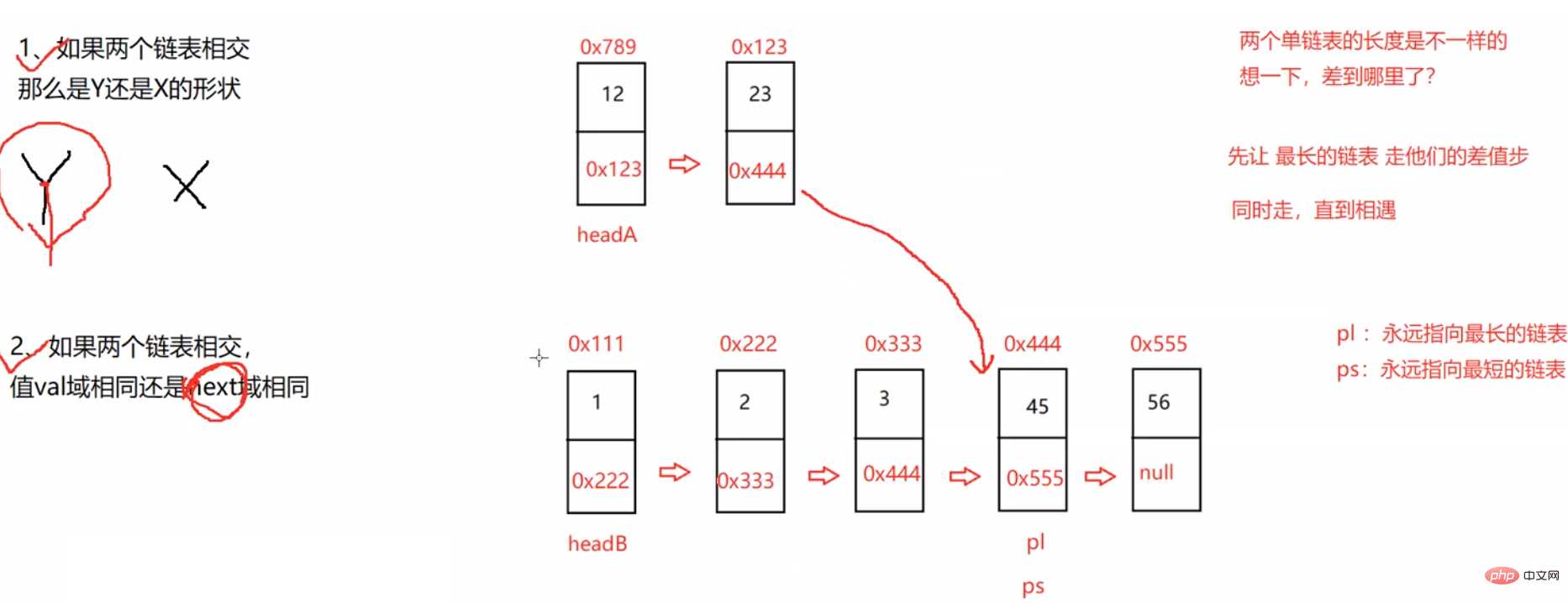

public ListNode getIntersectionNode(ListNode headA, ListNode headB) { if (headA == null || headB == null) { return null; } ListNode pl = headA; ListNode ps = headB; int lenA = 0; int lenB = 0; //求lenA的长度 while (pl != null) { lenA++; pl = pl.next; } pl = headA; //求lenB的长度 while (ps != null) { lenB++; ps = ps.next; } ps = headB; int len = lenA - lenB;//差值步 if (len < 0) { pl = headB; ps = headA; len = lenB - lenA; } //1、pl永远指向了最长的链表,ps永远指向了最短的链表 2、求到了插值len步 //pl走差值len步 while (len != 0) { pl = pl.next; len--; } //同时走直到相遇 while (pl != ps) { pl = pl.next; ps = ps.next; } return pl;}3.3.9 给定一个链表,判断链表中是否有环。

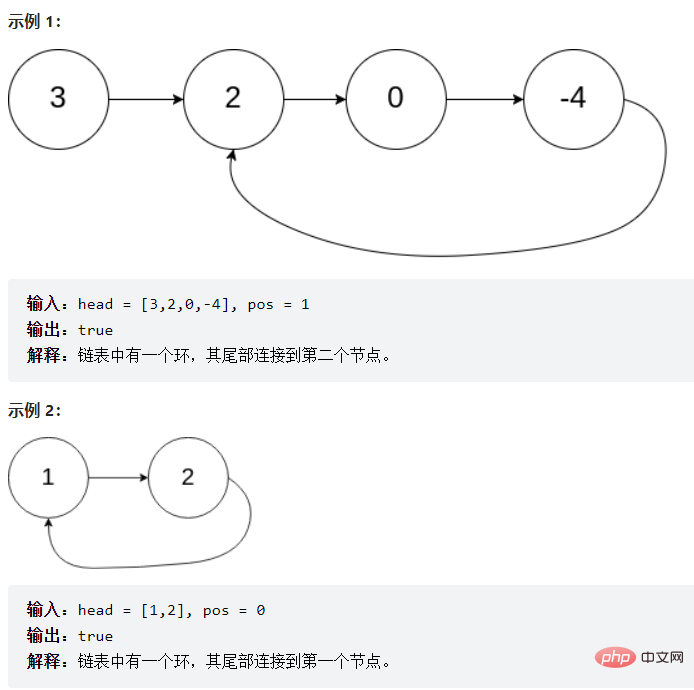

提问:为啥么fast一次走两步,不走三步?
答:如果链表只有两个元素他们则永远相遇不了(如上图的示例2),而且走三步的效率没有走两步的效率高。
public boolean hasCycle(ListNode head) { if (head == null) { return false; } ListNode fast = head; ListNode slow = head; while (fast != null && fast.next != null) { fast = fast.next.next; slow = slow.next; if (fast == slow) { return true; } } return false;}3.3.10 给定一个链表,返回链表开始入环的第一个节点。 如果链表无环,则返回 null

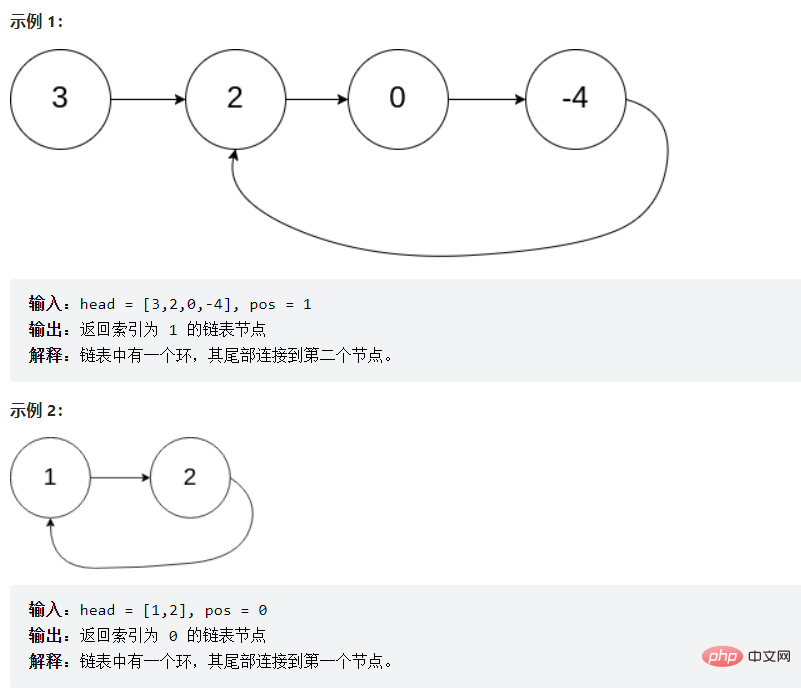

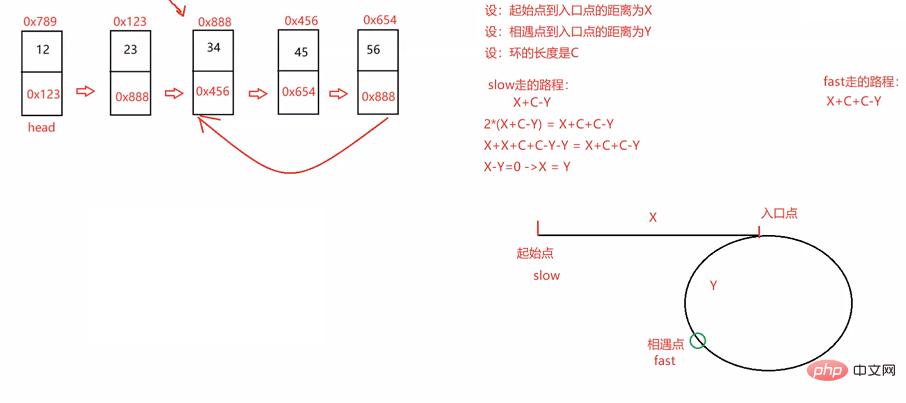
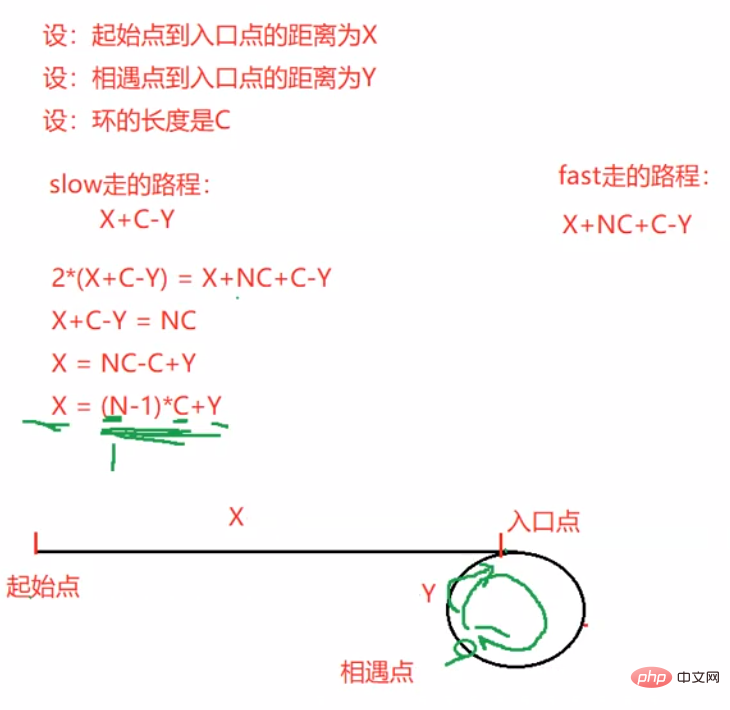
public ListNode detectCycle(ListNode head) { if (head == null) { return null; } ListNode fast = head; ListNode slow = head; while (fast != null && fast.next != null) { fast = fast.next.next; slow = slow.next; if (fast == slow) { break; } } if (fast == null || fast.next == null) { return null; } fast = head; while (fast != slow) { fast = fast.next; slow = slow.next; } return fast;}4. 顺序表和链表的区别和联系
4.1顺序表和链表的区别
顺序表:一白遮百丑
白:空间连续、支持随机访问
丑:
中间或前面部分的插入删除时间复杂度O(N)
增容的代价比较大。
链表:一(胖黑)毁所有
胖黑:以节点为单位存储,不支持随机访问
所有:
任意位置插入删除时间复杂度为O(1)
没有增容问题,插入一个开辟一个空间。
组织:
1、顺序表底层是一个数组,他是一个逻辑上和物理上都是连续的
2、链表是一个由若干结点组成的一个数据结构,逻辑上是连续的 但是在物理上[内存上]是不一定连续的。
操作:
1、顺序表适合,查找相关的操作,因为可以使用下标,直接获取到某个位置的元素
2、链表适合于,频繁的插入和删除操作。此时不需要像顺序表一样,移动元素。链表的插入 只需要修改指向即可。
3、顺序表还有不好的地方,就是你需要看满不满,满了要扩容,扩容了之后,不一定都能放完。所以,他空间上的利用率不高。
4.2数组和链表的区别
链表随用随取 要一个new一个
而数组则不一样 数组是一开始就确定好的
4.3AeeayList和LinkedList的区别
集合框架当中的两个类
集合框架就是将 所有的数据结构,封装成Java自己的类
以后我们要是用到顺序表了 直接使用ArrayList就可以。
推荐学习:《java视频教程》
위 내용은 Java 시퀀스 목록 및 연결 목록에 대한 자세한 설명과 예제의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!

