집 > 기사 > Java > Java에서 Prime 알고리즘의 원리와 구현(요약 공유)

Java에서 Prime 알고리즘의 원리와 구현(요약 공유)

WBOY앞으로: 2022-08-15 18:32:422388검색

이 기사에서는 java에 대한 관련 지식을 제공합니다. Prime 알고리즘은 연결된 그래프에서 최소 신장 트리를 구성하는 철저한 검색 알고리즘입니다. 이 글은 주로 Java에서 Prime 알고리즘의 원리와 구현을 소개합니다. 관심이 있다면 배울 수 있습니다.

추천 학습: "java 비디오 튜토리얼"

프림 알고리즘 소개

1. 마무리 터치

스패닝 트리 과정에서 이미 스패닝 트리에 있는 노드를 세트로 처리하고, 나머지 노드들을 다른 세트로 간주하고, 두 세트를 연결하는 엣지 중에서 가중치가 가장 작은 엣지를 선택할 수 있다.

2. 알고리즘 소개

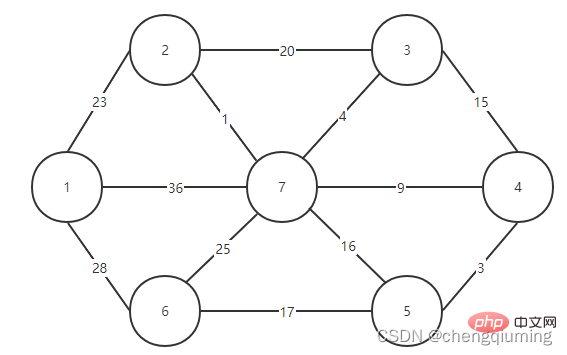
먼저 노드 1과 같은 노드를 선택하고 이를 집합 U, U={1}에 넣으면 나머지 노드는 V-U={2,3,4, 5입니다. ,6,7}, 집합 V는 그래프의 모든 노드 집합입니다.

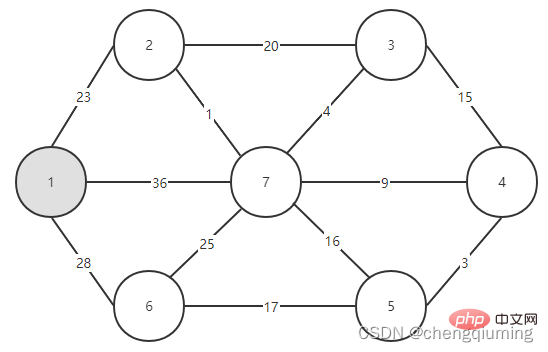
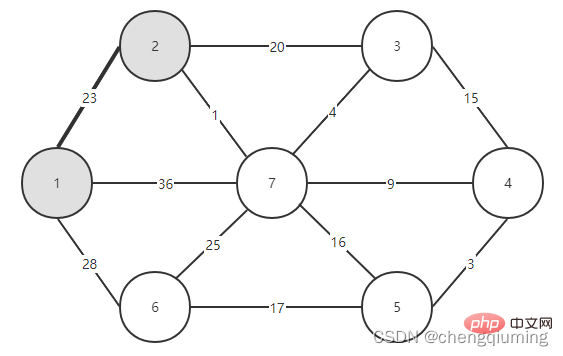
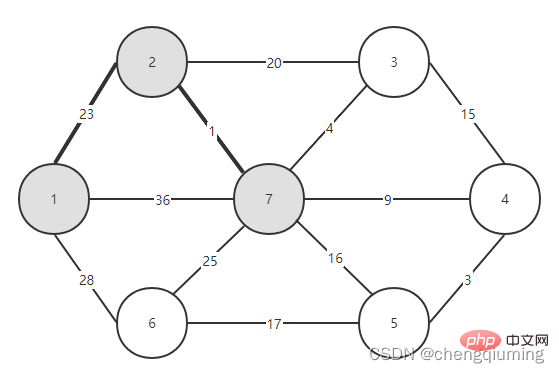
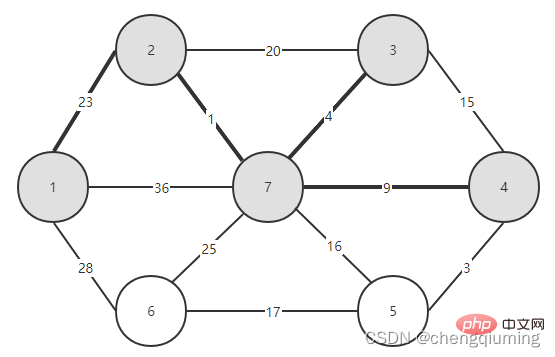
이제 두 집합(U, V-U)을 연결하는 간선 중 가중치가 가장 작은 간선을 확인하고, 가중치가 가장 작은 간선과 연결된 노드를 집합 U에 추가하면 됩니다. 위 그림에서 알 수 있듯이, 두 세트를 연결하는 3개의 간선 중에서 간선 1-2의 가중치가 가장 작습니다. 이를 선택하고 집합 U, U={1,2}, V - U=에 노드 2를 추가합니다. 아래 그림과 같이 {3,4,5,6}입니다.

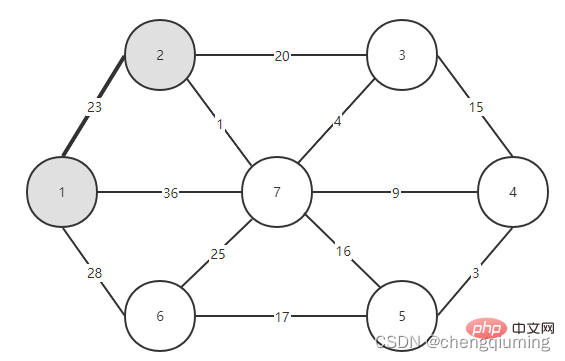
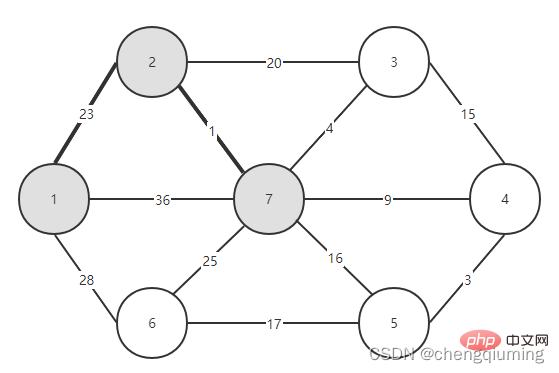
그런 다음 두 세트(U 및 V-U)를 연결하는 모서리 중 가중치가 가장 작은 모서리를 선택합니다. 위 그림에서 알 수 있듯이 두 세트를 연결하는 4개의 간선 중 노드 2에서 노드 7까지의 간선 가중치가 가장 작습니다. 이 간선을 선택하고 집합 U={1,2,7}에 노드 7을 추가합니다. , V-U ={3,4,5,6}.

이렇게 U=V가 끝날 때까지 계속하면, 선택된 Edge와 모든 Node로 구성된 그래프가 최소 스패닝 트리가 됩니다. 이것이 Prim의 알고리즘입니다.

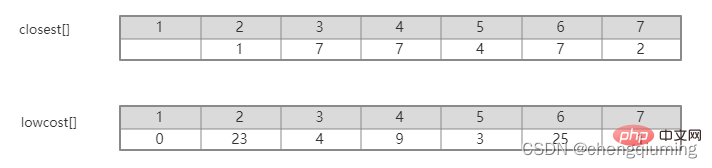
그림을 보면 집합 U에서 집합 U-V까지 어떤 간선이 가장 작은 가중치를 갖는지 쉽게 알 수 있습니다. 그러나 이러한 간선을 프로그램에서 모두 열거한 다음 최소값을 찾기에는 시간 복잡도가 너무 높습니다. 값. 이 문제는 배열을 설정하여 현명하게 해결할 수 있습니다. Closet[j]는 집합 V-U의 노드 j에서 집합 U까지의 가장 가까운 이웃 지점을 나타냅니다. Lowcost[j]는 집합 V-U의 노드 j에서 집합의 가장 가까운 이웃 지점까지의 간선 값을 나타냅니다. U를 설정합니다. 즉, 간선의 가중치(j, 가장 가까운[j])입니다.

예를 들어 위 그림에서 노드 7에서 U를 설정하는 가장 가까운 이웃 지점은 2, cloeest[7]=2입니다. 노드 7에서 가장 가까운 이웃 포인트 2까지의 에지 값은 1이며, 이는 에지(2,7)의 가중치이며 아래 그림과 같이 lowcost[7]=1로 기록됩니다.

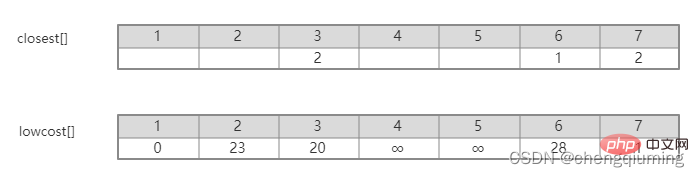
그러니 집합 V - U에서 가장 낮은 lowcost[] 노드를 찾으세요.

3. 알고리즘 단계

1. 초기화

집합 U={u0}, u0을 V에 속하게 하고, 가장 가까운[], lowcost[] 및 s[] 배열을 초기화합니다.

2. 집합 V-U에서 가장 작은 lowcost 값을 갖는 노드 t를 찾습니다. 즉, lowcost[t]=min{lowcost[j]}, j는 V-U에 속합니다. 집합 V-U에서 U를 연결합니다.

3. 집합 U에 노드 t를 추가합니다.

4. 집합 V - U가 비어 있으면 알고리즘이 종료되고, 그렇지 않으면 5단계로 이동합니다.

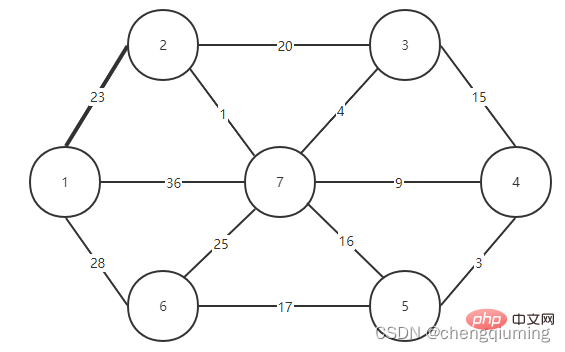
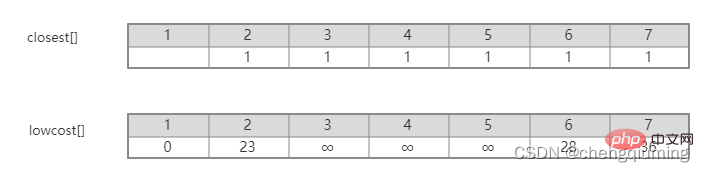
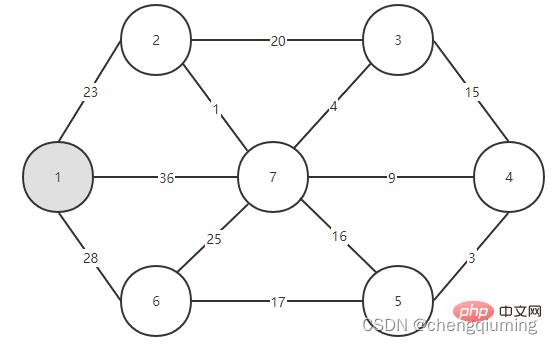
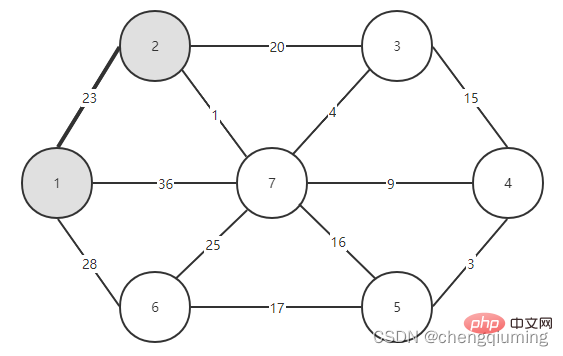
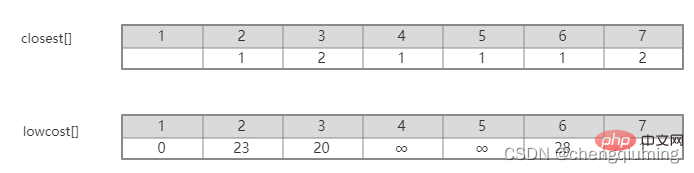
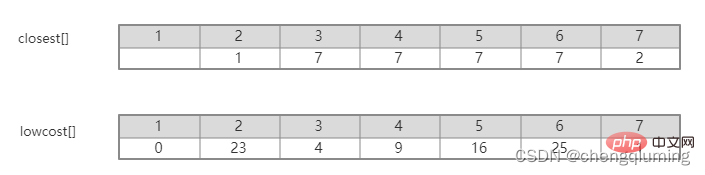
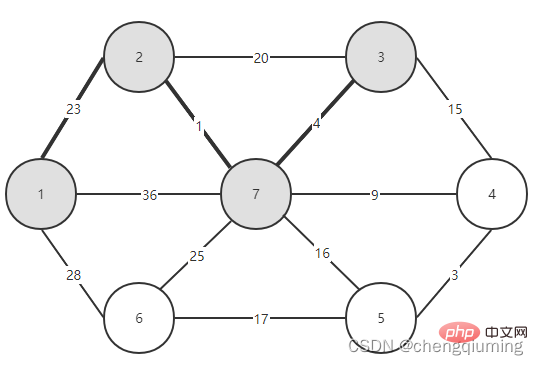
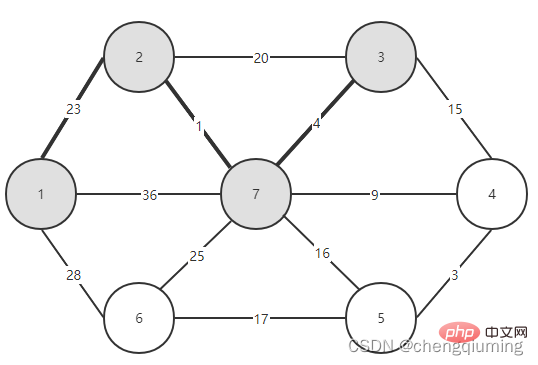
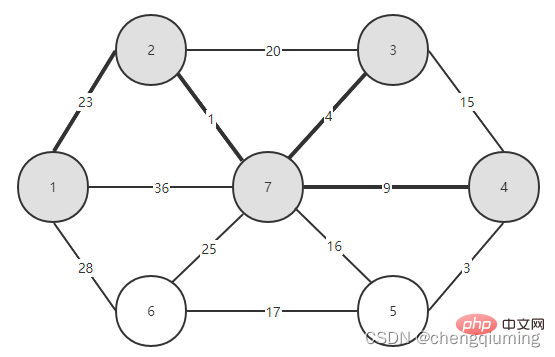
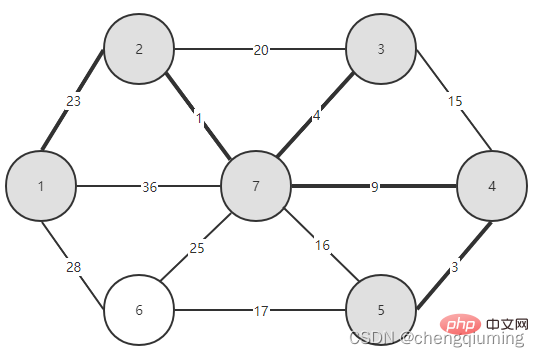
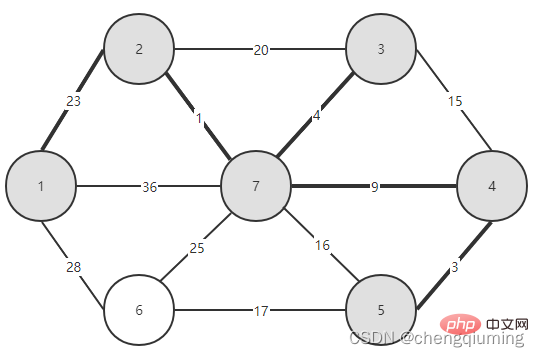
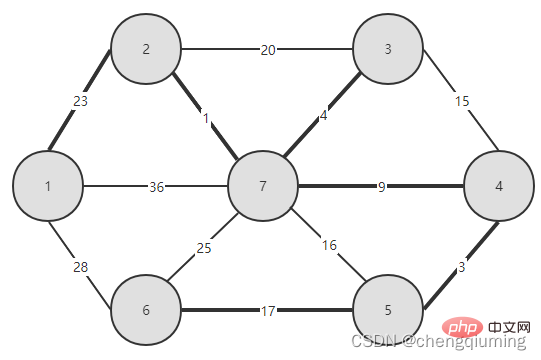
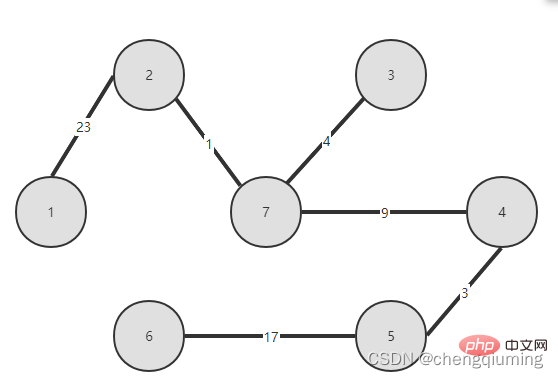
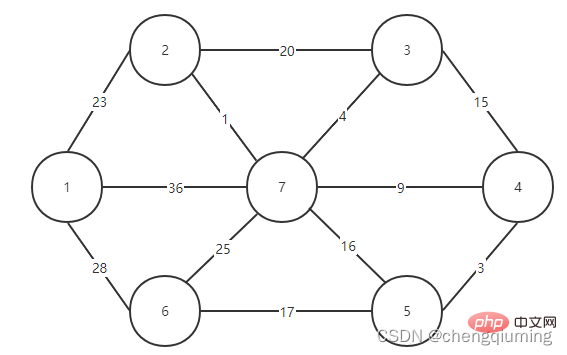
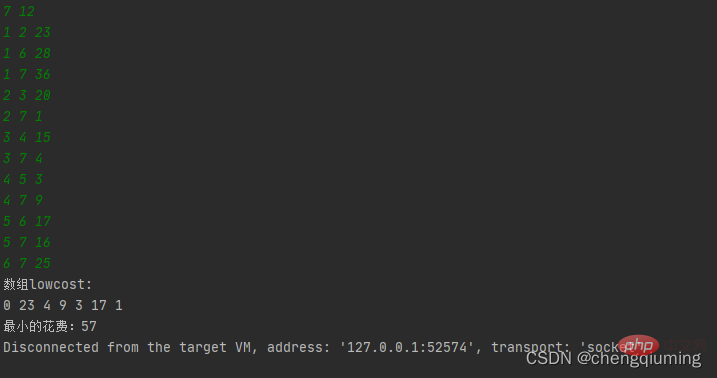
5. V-U 집합의 모든 노드 j에 대해 lowcost[] 및 close[]를 업데이트합니다. if(C[t][j]

위 단계를 따르면 마침내 가중치 합이 가장 작은 스패닝 트리를 얻을 수 있습니다.

4. 다이어그램

그래프 G=(V,E)는 아래 그림과 같이 무방향 연결 가중치 그래프입니다.

1 초기화. u0=1이라고 가정하고, 집합 U={1}, 집합 V-U={2,3,4,5,6,7}, s[1]=true라고 가정하고, 배열 Nearest[]를 초기화합니다. 노드 1을 제외하고, 다른 모든 노드는 1입니다. 이는 집합 V-U의 노드에서 집합 U까지 가장 가까운 이웃 지점이 모두 1임을 의미합니다. lowcost[]: 노드 1에서 집합 V-U의 노드까지의 간선 값입니다. 가장 가까운[] 및 lowcost[]는 아래 그림에 표시되어 있습니다.