JavaScript 바이너리 트리 및 다양한 순회 알고리즘에 대한 자세한 소개

이 글은 javascript에 대한 관련 지식을 제공합니다. 주로 JavaScript 바이너리 트리와 다양한 순회 알고리즘에 대해 자세히 소개합니다. 이 글은 특정 참조 가치가 있는 주제에 대한 자세한 소개를 제공합니다. . 모두에게 도움이 되기를 바랍니다.

[관련 권장 사항: javascript 비디오 튜토리얼, 웹 프론트 엔드]

이진 트리란 무엇입니까

이진 트리는 각 노드가 최대 2개의 하위 노드만 가질 수 있는 트리입니다. , 아래 그림과 같이:

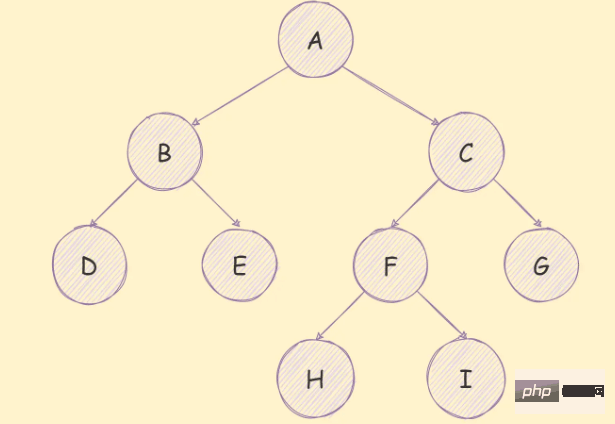
이진 트리는 다음과 같은 특성을 갖습니다.

• i번째 레이어는 최대 2^(i- 1) 노드; i层的节点最有只有2^(i-1)个；
• 如果这颗二叉树的深度为k，那二叉树最多有2^k-1个节点；
• 在一个非空的二叉树中，若使用n0表示叶子节点的个数，n2是度为2的非叶子节点的个数，那么两者满足关系n0 = n2 + 1。

满二叉树

如果在一个二叉树中，除了叶子节点，其余的节点的每个度都是2，则说明该二叉树是一个满二叉树，

如下图所示：

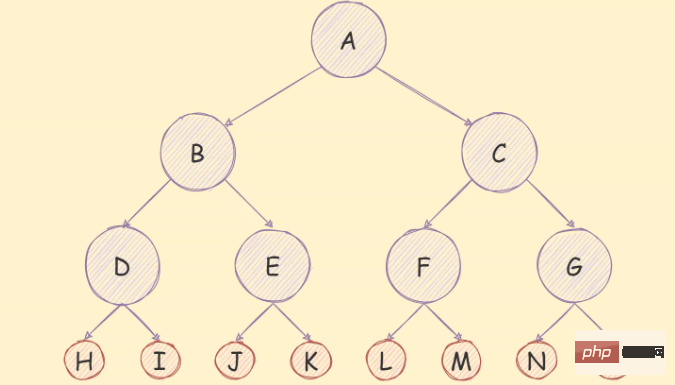
满二叉树除了满足普通二叉树特质，还具有如下几个特质：

• 满二叉树的的第n层具有2^(n-1)个节点；
• 深度为k的满二叉树一定存在2^k-1个节点，叶子节点的个数为2^(k-1)；
• 具有n个节点的满二叉树的深度为log_2^(n+1)。

完全二叉树

如果一个二叉树去掉最后一次层是满二叉树，且最后一次的节点是依次从左到右分布的，则这个二叉树是一个完全二叉树，

如下图所示：

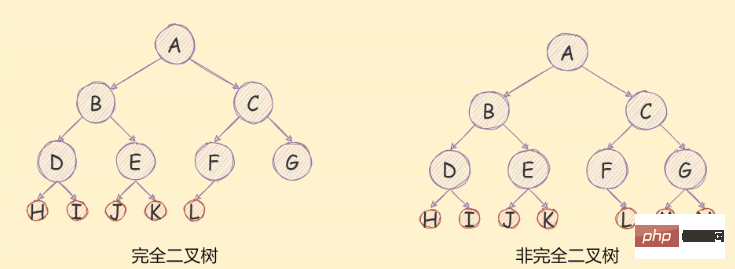
二叉树的存储

存储二叉树的常见方式分为两种，一种是使用数组存储，另一种使用链表存储。

数组存储

使用数组存储二叉树，如果遇到完全二叉树，存储顺序从上到下，从左到右，如下图所示：

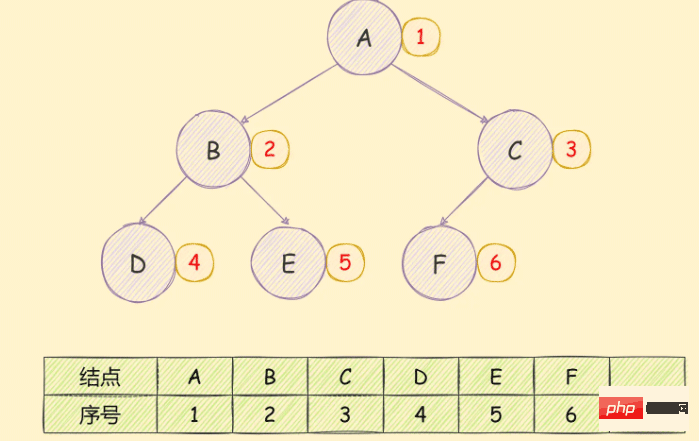
如果是一个非完全二叉树，如下图所示：

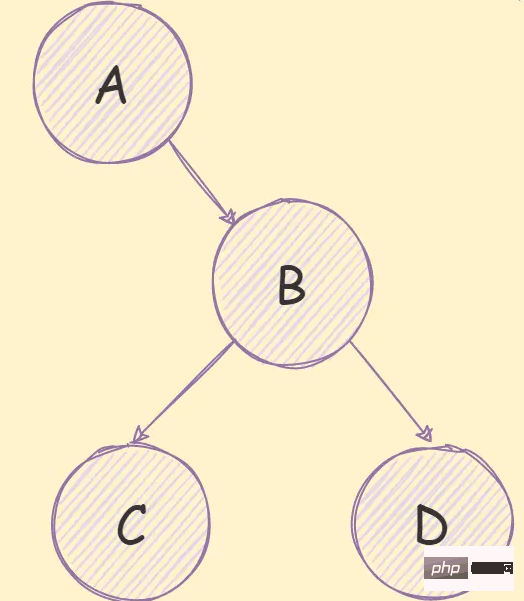
需要先将其转换为完全二叉树，然后在进行存储，如下图所示：

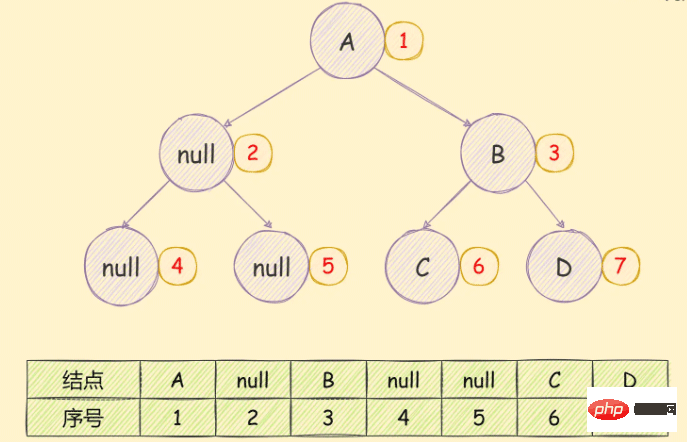
可以很明显的看到存储空间的浪费。

链表存储

使用链表存储通常将二叉树中的分为3个部分，如下图：

这三个部分依次是左子树的引用，该节点包含的数据，右子树的引用，存储方式如下图所示：

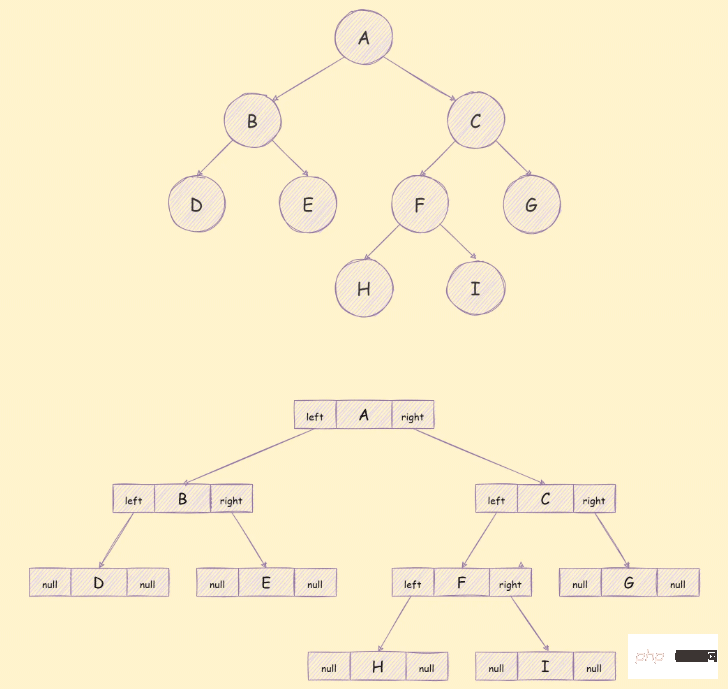
与二叉树相关的算法

以下算法中遍历用到的树如下：

// tree.js
const bt = {
  val: 'A',
  left: {
    val: 'B',
    left: { val: 'D', left: null, right: null },
    right: { val: 'E', left: null, right: null },
  },
  right: {
    val: 'C',
    left: {
      val: 'F',
      left: { val: 'H', left: null, right: null },
      right: { val: 'I', left: null, right: null },
    },
    right: { val: 'G', left: null, right: null },
  },
}
module.exports = bt

深度优先遍历

二叉树的深度优先遍历与树的深度优先遍历思路一致，思路如下：

• 访问根节点；
• 访问根节点的left
• 访问根节点的right
• 重复执行第二三步

实现代码如下：

const bt = {
  val: 'A',
  left: {
    val: 'B',
    left: { val: 'D', left: null, right: null },
    right: { val: 'E', left: null, right: null },
  },
  right: {
    val: 'C',
    left: {
      val: 'F',
      left: { val: 'H', left: null, right: null },
      right: { val: 'I', left: null, right: null },
    },
    right: { val: 'G', left: null, right: null },
  },
}

function dfs(root) {
  if (!root) return
  console.log(root.val)
  root.left && dfs(root.left)
  root.right && dfs(root.right) 
}
dfs(bt)
/** 结果
A B D E C F H I G
*/

广度优先遍历

实现思路如下：

• 创建队列，把根节点入队
• 把对头出队并访问
• 把队头的left和right
이 이진 트리의 깊이가 k이면 이진 트리는 최대 2^k-1 노드를 갖습니다. 비어 있지 않은 이진 트리에서 n0를 사용하여 리프 노드 수를 나타내고, n2는 차수가 2인 리프가 아닌 노드 수를 나타내고 두 개는 다음을 충족합니다. n0 = n2 + 1 관계.

완전 이진 트리

이진 트리에서 리프 노드를 제외하고 각 노드의 차수는 2이면 이진 트리가 완전 이진 트리

,

그림과 같이 아래 그림:

🎜🎜🎜만족스러운 것 외에도 일반 이진 트리의 특성, 완전 이진 트리도 다음과 같은 특성을 갖습니다. 🎜🎜🎜🎜완전 이진 트리의 n번째 수준은 2^(n-1)을 갖습니다. > 노드; 🎜🎜깊이는 k의 전체 이진 트리에는 <code>2^k-1 노드가 있어야 하며 리프 노드 수는 2^( k-1); 🎜🎜에는 가 있습니다. n 노드가 있는 전체 이진 트리의 깊이는 log_2^(n+1)입니다. 🎜🎜🎜완전 이진 트리🎜🎜🎜이진 트리가 마지막 레이어를 제거한 후 완전 이진 트리이고 마지막 노드가 🎜왼쪽에서 오른쪽으로 분포되어 있다면 이 이진 트리는 완전 이진 트리입니다. 🎜🎜🎜 아래 그림에 나와 있습니다: 🎜🎜🎜🎜🎜저장 이진 트리🎜🎜이진 트리 저장 방법에는 두 가지 일반적인 방법이 있습니다. 하나는 🎜배열 저장🎜을 사용하는 것이고, 다른 하나는 연결 목록 저장을 사용하는 것입니다. 🎜🎜배열 저장🎜🎜🎜배열을 사용하여 이진 트리를 저장하면 아래 그림과 같이 저장 순서는 위에서 아래, 왼쪽에서 오른쪽입니다. 🎜🎜🎜🎜🎜🎜아래와 같이 불완전한 이진 트리인 경우: 🎜🎜🎜🎜🎜🎜 아래 그림과 같이 먼저 이진 트리를 완성한 다음 저장합니다. 표시: 🎜🎜🎜🎜🎜 확연히 눈에 띄는 수납공간 낭비. 🎜🎜연결된 목록 저장소🎜🎜🎜연결된 목록 저장소를 사용하면 이진 트리는 일반적으로 아래와 같이 3부분으로 나뉩니다. 🎜🎜🎜🎜🎜🎜이 세 부분은 차례로 왼쪽 하위 트리에 대한 참조, 노드에 포함된 데이터, 오른쪽 하위 트리에 대한 참조입니다. 방법은 아래 그림과 같습니다. 🎜🎜 🎜🎜 🎜이진 트리 관련 알고리즘🎜🎜🎜다음 알고리즘 순회에 사용되는 트리는 다음과 같습니다🎜:🎜

function bfs(root) {
  if (!root) return
  const queue = [root]
  while (queue.length) {
    const node = queue.shift()
    console.log(node.val)
    node.left && queue.push(node.left)
    node.right && queue.push(node.right)
  }
}
bfs(bt)
/** 结果
A B C D E F G H I
 */

🎜깊이 우선 순회🎜🎜🎜이진 트리의 깊이 우선 순회는 깊이 우선 순회와 일치합니다. 아이디어는 다음과 같습니다.🎜🎜🎜🎜루트 노드를 방문하세요. 🎜🎜루트 노드 코드의 을 방문하세요.🎜🎜루트의 오른쪽에 액세스하세요. node🎜🎜두 번째와 세 번째 단계를 반복합니다🎜🎜🎜🎜구현 코드는 다음과 같습니다.🎜🎜

const bt = require('./tree')

function preorder(root) {
  if (!root) return
  console.log(root.val)
  preorder(root.left)
  preorder(root.right)
}
preorder(bt)
/** 结果
A B D E C F H I G
*/

🎜Breadth-first traversal🎜🎜🎜구현 아이디어는 다음과 같습니다. 🎜🎜🎜🎜큐 생성, 루트 노드 추가 🎜🎜상대를 대기열에서 제거하고 접근하세요 🎜🎜대기열의 선두에 왼쪽과 오른쪽을 순서대로 입력하세요🎜🎜반복 queue isempt🎜🎜🎜🎜구현 코드는 다음과 같습니다.🎜🎜

// 非递归版
function preorder(root) {
  if (!root) return
  // 定义一个栈，用于存储数据
  const stack = [root]
  while (stack.length) {
    const node = stack.pop()
    console.log(node.val)
    /* 由于栈存在先入后出的特性，所以需要先入右子树才能保证先出左子树 */
    node.right && stack.push(node.right)
    node.left && stack.push(node.left)
  }
}
preorder(bt)
/** 结果
A B D E C F H I G
*/

🎜선주문 순회🎜🎜🎜이진 트리의 선주문 순회 구현 아이디어는 다음과 같습니다.🎜🎜

• 访问根节点;
• 对当前节点的左子树进行先序遍历；
• 对当前节点的右子树进行先序遍历；

如下图所示：

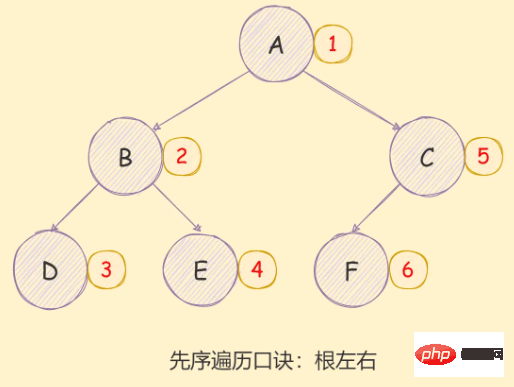
递归方式实现如下：

const bt = require('./tree')

function preorder(root) {
  if (!root) return
  console.log(root.val)
  preorder(root.left)
  preorder(root.right)
}
preorder(bt)
/** 结果
A B D E C F H I G
*/

迭代方式实现如下：

// 非递归版
function preorder(root) {
  if (!root) return
  // 定义一个栈，用于存储数据
  const stack = [root]
  while (stack.length) {
    const node = stack.pop()
    console.log(node.val)
    /* 由于栈存在先入后出的特性，所以需要先入右子树才能保证先出左子树 */
    node.right && stack.push(node.right)
    node.left && stack.push(node.left)
  }
}
preorder(bt)
/** 结果
A B D E C F H I G
*/

中序遍历

二叉树的中序遍历实现思想如下：

• 对当前节点的左子树进行中序遍历；
• 访问根节点;
• 对当前节点的右子树进行中序遍历；

如下图所示：

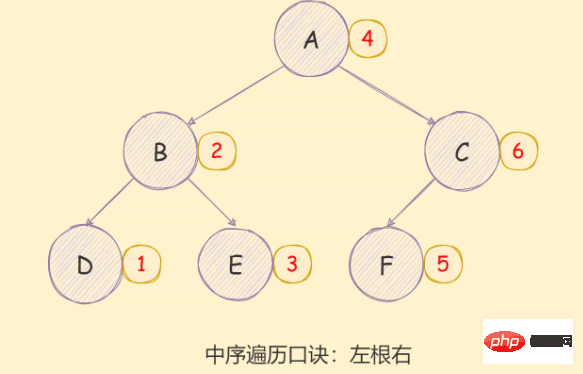
递归方式实现如下：

const bt = require('./tree')

// 递归版
function inorder(root) {
  if (!root) return
  inorder(root.left)
  console.log(root.val)
  inorder(root.right)
}
inorder(bt)

/** 结果
D B E A H F I C G
*/

迭代方式实现如下：

// 非递归版
function inorder(root) {
  if (!root) return
  const stack = []
  // 定义一个指针
  let p = root
  // 如果栈中有数据或者p不是null，则继续遍历
  while (stack.length || p) {
    // 如果p存在则一致将p入栈并移动指针
    while (p) {
      // 将 p 入栈，并以移动指针
      stack.push(p)
      p = p.left
    }

    const node = stack.pop()
    console.log(node.val)
    p = node.right
  }
}
inorder(bt)
/** 结果
D B E A H F I C G
*/

后序遍历

二叉树的后序遍历实现思想如下：

• 对当前节点的左子树进行后序遍历；
• 对当前节点的右子树进行后序遍历；
• 访问根节点;

如下图所示：

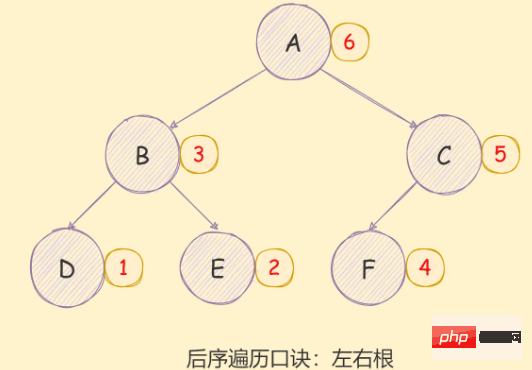
递归方式实现如下：

const bt = require('./tree')

// 递归版
function postorder(root) {
  if (!root) return
  postorder(root.left)
  postorder(root.right)
  console.log(root.val)
}
postorder(bt)
/** 结果
D E B H I F G C A
*/

迭代方式实现如下：

// 非递归版
function postorder(root) {
  if (!root) return
  const outputStack = []
  const stack = [root]
  while (stack.length) {
    const node = stack.pop()
    outputStack.push(node)
    // 这里先入left需要保证left后出，在stack中后出，就是在outputStack栈中先出
    node.left && stack.push(node.left)
    node.right && stack.push(node.right)
  }
  while (outputStack.length) {
    const node = outputStack.pop()
    console.log(node.val)
  }
}
postorder(bt)
/** 结果
D E B H I F G C A
*/

【相关推荐：javascript视频教程、web前端】

위 내용은 JavaScript 바이너리 트리 및 다양한 순회 알고리즘에 대한 자세한 소개의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!