이진 트리 순회 및 논리 연산 방법에 대한 자세한 설명
- 醉折花枝作酒筹앞으로
- 2021-07-26 17:43:341756검색
우선, 우리가 공부하는 주요 내용이 이진 트리라는 점을 먼저 설명해야 합니다. 왜냐하면 이진 트리는 시험이든 면접이든 반드시 알아야 하고 배워야 하는 트리의 가장 일반적인 응용이기 때문입니다. 콘텐츠.

먼저 트리의 연산을 배우기에 앞서 트리의 연산의 핵심이 "순회"라는 것을 먼저 이해해야 합니다. 왜 그런 말을 합니까? 스택 및 큐와 달리 트리 구조는 더 이상 1차원이 아니며 가지와 다양한 각도를 가지며 더 중요한 것은 계층 구조의 개념을 가지고 있다는 것입니다.
1차원 공간에 있는 것들은 길이만 있고 높이가 없는 공통 "선"이며, 이 길이는 유일한 차원입니다. 스택과 큐는 분명히 1차원입니다. 트리는 계층 개념 때문에 "높이"를 갖게 되었습니다. 즉, 2차원 개념으로 업그레이드되었습니다. 이전 글에서 소개한 명사뭉치처럼 "나무의 높이(깊이)"라는 개념이 있습니다.
트리를 순회할 수 있게 되면 순회를 기반으로 트리 노드에서 추가, 삭제, 수정 및 기타 작업을 수행할 수 있습니다. 이러한 기본 논리 작업은 모두 순회를 기반으로 합니다. 논리 연산도 순회로 시작되지 않나요? 팝핑, 스택 진입, 큐 제거 또는 큐 추가 등 우리는 모두 고정 순회 규칙(FILO, FIFO)을 기반으로 합니다.
2차원적인 것은 어떻게 횡단하느냐가 관건입니다. 1차원 데이터 구조는 순차적으로 순회하면 되지만, 2차원 데이터 결과는 노드들 사이에 계층적 관계가 있기 때문에 단순히 순서대로 하나씩 순회할 수 없으므로 현재 노드에 데이터가 없는 경우를 고려해야 합니다. 하위 노드, 순회 작업 중에 무엇을 해야 합니까?
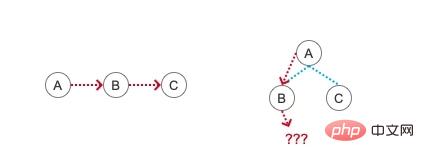
다행히도 우리는 거인의 어깨 위에 서서 이 지식을 배웁니다. 많은 선배들이 우리를 위해 매우 간단한 트리 순회 방법을 요약했습니다. 얼마나 간단합니까? 먼저 본론에서 벗어나 이전 기사에서 보여드린 이진 트리인 트리를 구축하는 방법을 살펴보겠습니다.
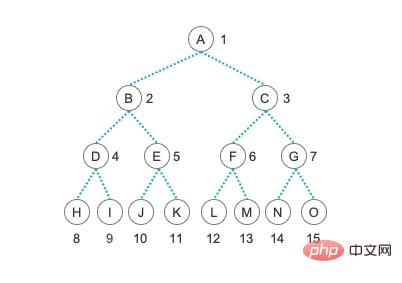
이진 트리의 체인 스토리지 구조
이진 트리의 체인 스토리지를 사용하는 것은 매우 간단하고 시각적입니다. 이진 트리의 순차적 스토리지에 대한 질문은 다음 기사에서 설명할 예정입니다. 순차 저장소를 사용합니다.
class BiTree
{
public $data;
public $lChild;
public $rChild;
}실제로 체인스토리지에서는 트리를 저장하기 위해 노드를 하나씩 사용합니다. 각 이진 트리 노드에는 데이터 속성인 데이터 필드가 있습니다. 다른 두 속성은 두 개의 분기된 포인터, 즉 이 노드의 왼쪽 자식 노드 lChild와 오른쪽 자식 노드 rChild로 간주될 수 있습니다.
스택과 큐를 비교하면 다음 노드를 왼쪽 및 오른쪽 하위 노드로 대체했을 뿐입니다. 본질적으로 스택 및 큐와 크게 다르지 않습니다. 직설적으로 말하면, 데이터 구조의 관점에서 볼 때 우리는 여전히 1차원 저장소를 사용하여 2차원 개념을 표현하고 있으며, 이 개념의 변형은 개념 이해의 관점에서 시작해야 합니다.
이진 트리 구축
// 建立二叉树
function CreateBiTree($arr, $i)
{
if (!isset($arr[$i])) {
return null;
}
$t = new BiTree();
$t->data = $arr[$i];
$t->lChild = CreateBiTree($arr, $i * 2);
$t->rChild = CreateBiTree($arr, $i * 2 + 1);
return $t;
}이런 간단한 방법으로 체인 이진 트리 구축을 완료할 수 있습니다. 친구 여러분, 주의 깊게 살펴보시기 바랍니다. 이 간단한 트리 만들기 작업에는 실제로 많은 미스터리가 포함되어 있습니다.
우리는 A, B, C, D, E를 순서대로 입력하는 것과 같이 트리의 각 노드를 순서대로 표현하기 위해 배열을 사용합니다. ... (트리의 순차적 저장소에서 다시 볼 수 있습니다)
할당된 내용은 현재 $i 첨자의 데이터입니다. 왼쪽에 값을 할당할 때 재귀 연산을 수행했으며 맞아요
스택을 배울 때 우리는 "재귀"가 스택 유형의 연산이라는 것을 배웠습니다. 따라서 이 코드에서는 스택 형태로 트리를 만듭니다
주의하세요. 그리고 나는 2 + 1이죠, 그렇죠? 이진 트리의 속성 5를 검토하세요
마지막으로 이 방법이 연결된 트리 구조를 성공적으로 구축할 수 있는지 테스트합니다.
$treeList = ['', 'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K', 'L', 'M', 'N', 'O']; $tree = CreateBiTree($treeList, 1); print_r($tree); // BiTree Object // ( // [data] => A // [lChild] => BiTree Object // ( // [data] => B // [lChild] => BiTree Object // ( // [data] => D // [lChild] => BiTree Object // ( // [data] => H // [lChild] => // [rChild] => // ) // [rChild] => BiTree Object // ( // [data] => I // [lChild] => // [rChild] => // ) // ) // [rChild] => BiTree Object // ( // [data] => E // [lChild] => BiTree Object // ( // [data] => J // [lChild] => // [rChild] => // ) // [rChild] => BiTree Object // ( // [data] => K // [lChild] => // [rChild] => // ) // ) // ) // [rChild] => BiTree Object // ( // [data] => C // [lChild] => BiTree Object // ( // [data] => F // [lChild] => BiTree Object // ( // [data] => L // [lChild] => // [rChild] => // ) // [rChild] => BiTree Object // ( // [data] => M // [lChild] => // [rChild] => // ) // ) // [rChild] => BiTree Object // ( // [data] => G // [lChild] => BiTree Object // ( // [data] => N // [lChild] => // [rChild] => // ) // [rChild] => BiTree Object // ( // [data] => O // [lChild] => // [rChild] => // ) // ) // ) // )
인쇄된 내용이 아주 선명해야겠죠? 노드 A에는 두 개의 왼쪽 및 오른쪽 자식 노드, 즉 B와 C가 있고, 노드 B에는 두 개의 왼쪽 및 오른쪽 자식 노드(각각 D와 E)가 있습니다. 최종 구조는 위의 이진 트리 다이어그램의 구조와 정확히 동일합니다. 여기서 우리는 또한 전달된 배열에 대해 첫 번째 요소, 즉 첨자가 0인 데이터를 비어 있는 상태로 제공하고 요소인 두 번째 요소부터 트리를 구축한다는 사실에도 주목할 필요가 있습니다. 1개의 첨자로. 이는 또한 이진 트리의 속성 5를 직관적이고 편리하게 활용하여 이 트리를 빠르게 구축할 수 있도록 하기 위함이다.
二叉树的遍历
说完二叉树的建树了,其实我们就已经接触到了一种二叉树的遍历形式。注意看我们建树方法中的代码,我们是先给结点的 data 赋值,然后建立这个结点的左、右孩子结点,并为它们赋值后再继续使用同样的操作一路建立完成所有的结点。现在,我们将这个操作反过来,不是建立结点,而是读取这些结点的内容,先读取结点的内容,然后再读取这个结点左右孩子结点的内容,这就是“先序遍历”。
先序遍历
/**
* 前序遍历
*/
function PreOrderTraverse(?BiTree $t)
{
if ($t) {
echo $t->data, ',';
PreOrderTraverse($t->lChild);
PreOrderTraverse($t->rChild);
}
}
PreOrderTraverse($tree);
// A,B,D,H,I,E,J,K,C,F,L,M,G,N,O,是不是很神奇?就连建树我们竟然也使用的是同一种遍历的方法,可以看出对于二叉树这种复杂的数据结构来说,遍历的重要作用了吧。
大家可以看一个遍历读取出来的结点顺序,貌似和我们输入的顺序不一样呀!没错,先序遍历是通过递归,先按一个方向走到底,当这个结点没有子结点之后,通过递归栈的特性再向上弹出。并且在遍历孩子结点之前先输出当前这个结点的内容。注意,这一句话很重要!所以我们的顺序就是 A,B,D,H ,当 H 没有子结点之后,我们就回到父结点 D 再进入它的右子结点 I ,具体顺序可以参考下图:
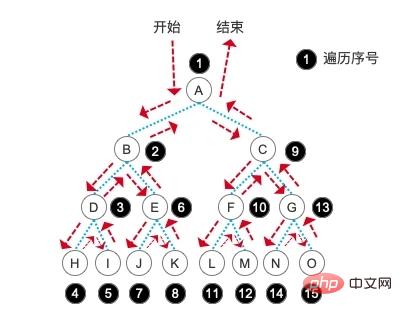
我们代码中的先序遍历和先序建树的结点顺序是完全不一样的,这一点也是要搞清楚的。建树的过程我们根据二叉树的 性质5 直接为它指定了数据下标。而在遍历过程中则是一个结点一个结点的去扫描遍历整颗树的。
中序遍历
顾名思义,中序遍历其实就是在遍历完左孩子结点之后再输出当前这个结点的内容,所以我们只需要微调先序遍历的代码即可。
/**
* 中序遍历
*/
function InOrderTraverse(?BiTree $t)
{
if ($t) {
InOrderTraverse($t->lChild);
echo $t->data, ',';
InOrderTraverse($t->rChild);
}
}
InOrderTraverse($tree);
// H,D,I,B,J,E,K,A,L,F,M,C,N,G,O,中序遍历的步骤就是我们会直接先走到最左边的子结点,当遇到最后一个结点时,输出内容,也就是图中的 H 结点,接着回到它的父结点 D 结点,这时根据中序的原理输出 D ,再进入它的右孩子结点并输出 I 。
D 结点的子树及它本身遍历完成后,返回 D 结点的上级结点 B 结点,输出 B ,然后进入 B 结点的右孩子结点 E 。再次进入到 E 的最左孩子结点 J ,然后参考 D 结点的遍历形式完成整颗树的遍历。具体顺序参考下图:
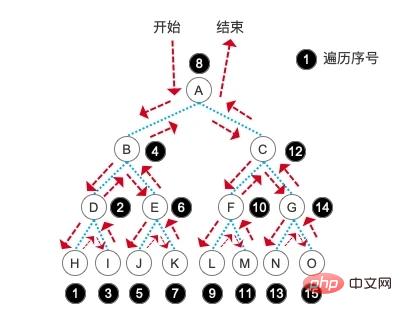
后序遍历
在学习了先序和中序之后,从名字就可以看出来后序就是在遍历完一个结点的左右孩子之后最后输出这个结点的内容,代码当然也是简单地微调一下就可以了。
/**
* 后序遍历
*/
function PostOrderTraverse(?BiTree $t)
{
if ($t) {
PostOrderTraverse($t->lChild);
PostOrderTraverse($t->rChild);
echo $t->data, ',';
}
}
PostOrderTraverse($tree);
// H,I,D,J,K,E,B,L,M,F,N,O,G,C,A,具体原理就不详细说明了,相信在学习了先序和中序之后,你一定能马上想明白后序遍历到底是什么意思了。直接上图:
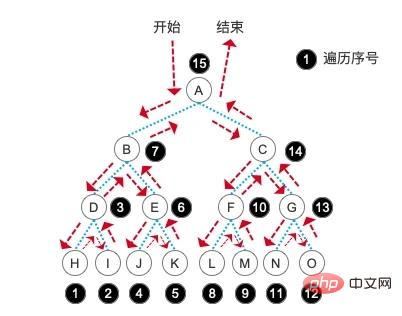
层序遍历
最后,我们要讲的就是层序遍历。既然有“层”这个关键字了,相信大家马上就能联想到,是不是一层一层地去遍历啊!没错,层序遍历就是这个意思,我们按照树的层次,一层一层地输出相应的结点信息。需要注意的,在这里我们会用到队列,而不是栈了。
/**
* 层序遍历
*/
$q = InitLinkQueue();
function LevelOrderTraverse(?BiTree $t)
{
global $q;
if (!$t) {
return;
}
EnLinkQueue($q, $t);
$node = $q;
while ($node) {
$node = DeLinkQueue($q);
if ($node->lChild) {
EnLinkQueue($q, $node->lChild);
}
if ($node->rChild) {
EnLinkQueue($q, $node->rChild);
}
echo $node->data, ',';
}
}
LevelOrderTraverse($tree);
// A,B,C,D,E,F,G,H,I,J,K,L,M,N,O,InitLinkQueue() EnLinkQueue() 、 EnLinkQueue() 这些都是我们之前学习队列的时候所写的对于队列的逻辑操作方法。是不是很开心呀,之前的知识又用上了。层序遍历的核心思想就是运用队列的概念,遇到一个结点,就把这个结点入队,然后判断它是否有子结点,然后相继把子结点入队。
每遍历一个结点,就把队首的结点出队,这样就完成了按树的层次遍历的能力。文字说明还是太抽象,我们还是通过图片来展示这一过程:
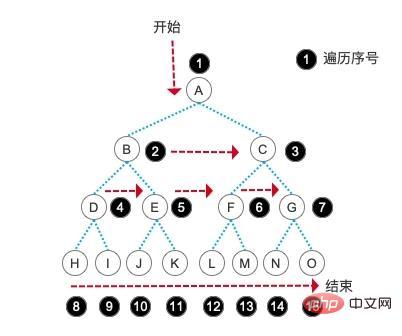
大家有没有发现,层序遍历的输出结果就和我们建树时的数组顺序完全相同了。很好玩吧,所以说代码的世界总是有无穷的乐趣等着我们去发现哦!
总结
今天的内容有没有懵圈?如果懵圈了就多找资料好好研究一下,先序、中序、后序都是利用栈来进行树的结点遍历的,而层序遍历则是利用了队列。一环套一环呀,前面学习的内容都派上用场了吧!不过这只是个开始,在学习图的时候,我们会在深度遍历和广度遍历中再次看到栈和队列的身影,它们可都是亲戚哦。
这四种遍历方式在考试和面试中也是经常出现的,不管是它们的原理还是画图或者是根据图形来写出各种遍历的顺序,都是非常常见的考核内容,所以大家在这篇文章入门的基础上还是要更加深入的去根据一些教材来深入的理解这几种遍历,熟练的掌握它们。
测试代码:
https://github.com/zhangyue0503/Data-structure-and-algorithm/blob/master/4.树/source/4.2二叉树的遍历及逻辑操作.php
推荐学习:php视频教程
위 내용은 이진 트리 순회 및 논리 연산 방법에 대한 자세한 설명의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!

