3분 안에 트리와 이진 트리에 대해 알아보세요

컴퓨터 분야에서 우리가 매일 다루는 [폴더]와 데이터베이스에 저장하는 데이터는 모두 나무의 전형적인 응용입니다. 오늘 우리는 트리와 이진 트리의 보다 이론적 정의와 그 속성 및 특징에 대해 배울 것입니다.

Tree

위의 실생활 예에서 트리 구조가 트리 구조의 일부 특성을 요약할 수 있음을 알 수 있습니다.

트리(Tree)는 N(N>0) 노드의 유한 집합입니다. 이는 빈 트리(N=0)이거나 비어 있지 않은 트리 T입니다.

이 정의에서 우리는 두 가지 문제를 명확히 해야 합니다. 첫째, 트리에는 노드가 있어야 하고, 둘째, 노드 수에 따라 빈 트리와 비어 있지 않은 트리의 두 가지 유형으로 나눌 수 있습니다. 그러나 이것은 가장 기본적인 정의일 뿐이며 몇 가지 속성을 가지고 있습니다.

루트라는 노드가 하나만 있습니다.

즉, 이 트리는 트리의 루트와 같은 특정 노드에서 확장되어야 합니다. 그것으로부터 바깥쪽으로 가지가 나기 시작합니다.

루트 노드를 제외한 나머지 노드는 m(m>0)의 분리된 유한 집합 T1, T2..., Tm으로 나눌 수 있습니다. 각 집합 자체가 트리이며 루트(SubTree)라고 합니다.

이 단락은 이해하기 쉽지 않을 수 있습니다. 사실 직설적으로 말하면 각 노드에는 상위 노드가 하나만 있고 상위 노드가 여러 개 있을 수 없습니다. 마찬가지로 수평 노드 사이에는 연결이 있을 수 없지만 여러 개의 하위 노드를 가질 수 있습니다.

나무의 정의는 아래 그림을 참조하세요.

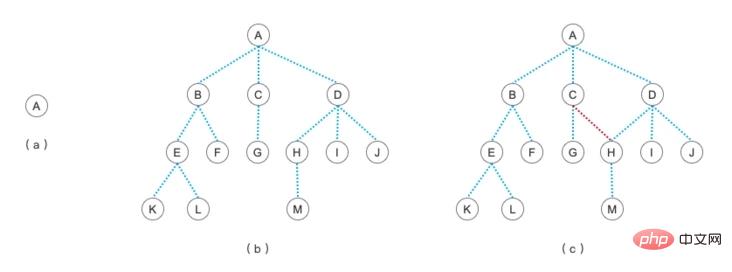
위 사진은 표준나무와 비표준나무의 모습을 간략하게 나열한 것입니다. 그 중:

• (a)는 루트 노드가 하나만 있는 트리입니다. 노드가 하나인 한 트리 구조라고 부를 수 있습니다.

• (b)는 표준 트리 구조입니다

• (c), C 노드와 H 노드 사이에 연결선이 있다는 점에 유의하세요. 이것은 트리가 아닙니다. 노드는 트리라고 불리는 상위 노드를 하나만 가질 수 있습니다. 그림]

트리 관련 용어

스택 푸시(into) 및 팝 아웃, 큐 엔큐 및 디큐에 비해 트리 관련 용어는 훨씬 더 복잡합니다. 무슨 일이 있어도 먼저 이 용어들을 기억해야 합니다. 그렇지 않으면 나중에 논의할 용어가 여러분을 더 혼란스럽게 만들 뿐입니다. 하지만 잠시 동안 기억하지 못하더라도 상관없습니다. 처음에는 대략적인 인상을 받았다가 나중에 학습 과정에서 그것을 접했을 때 다시 검토해 볼 수 있습니다. 이렇게 하면 인상이 더욱 깊어질 것입니다. .

• 노드에는 데이터 집합이 포함될 수도 있고, 다른 노드를 가리키는 분기가 포함될 수도 있습니다. (b) A, B, C, D, E 등. 그림에서 이것은 노드의 등급입니다.

• : 노드가 소유한 하위 트리의 수를 노드의 등급이라고 합니다. 실제로는 하위 하위 노드가 몇 개 있는지의 정도입니다. 그림에서 노드 C의 차수는 1이고 노드 D의 차수는 3

• 트리의 차수: 트리에 있는 각 노드의 차수 최대값은 자식 노드가 가장 많은 차수이며, 이는 트리의 차수입니다. (b) 그림에서 이 트리의 차수는 3

• Leaves: 차수가 0인 노드, 즉 자식 노드가 없는 노드, (b) K, L, F, G , M, 그림에서 I와 J는 이 트리의 리프 노드입니다

• 부모와 자식: 노드의 자식 노드는 이 자식 노드의 자식이고, 현재 노드는 부모입니다. (b) 그림에서 D의 자식은 H, I, J이고 H, I, J의 부모는 D

• 레벨: 루트 노드부터 계산하면 루트 노드가 첫 번째 레벨이고, 그 자식은 (b) 그림에서 G 노드의 수준은 3이고, (a) 그림의 모든 수준은 1

• 트리의 깊이(높이)입니다. : 트리의 현재 최대 레벨, 분명히 (b) 그래프의 깊이는 4

• 형제, 조상 및 후손: 형제 노드는 이 노드의 부모이며 동일한 조상 노드는 루트에서 왔습니다. 노드를 지정된 노드로 도로를 통과하는 모든 노드는 특정 노드에서 시작하여 대상 노드에 도달하는 도로의 모든 노드입니다. (b) 그림에서 E와 F는 형제이고, E의 조상은 A와 B이며, E의 자손은 K 또는 L

• 사촌입니다. 모든 노드는 같은 수준에 있지만 부모가 다릅니다. 또한 모두 사촌입니다. 그림 (b)에서 G의 사촌은 E와 F입니다. 또한 H, I, J도 사촌입니다

이진 트리

트리에 대한 개념을 어느 정도 이해한 후 더 나아가겠습니다. 데이터 구조와 알고리즘에서 가장 중요한 트리 형식이기도 한 또 다른 개념인 이진 트리를 알아보세요.

일반적으로 트리의 모양은 계속 변할 수 있습니다. 예를 들어 한 노드에는 3개의 하위 노드가 있고 다른 노드에는 300개의 하위 노드가 있을 수 있습니다. 규칙이 없는 이러한 트리는 실제로 작동하기가 매우 까다로우며 이진 트리의 정의는 트리의 속성 외에도 하나 이상의 내용을 갖습니다. 이진 트리의 각 노드는 최대 즉, 전체 이진 트리의 차수는 2여야 하며 모든 노드의 차수는 2를 초과할 수 없습니다. 이진 트리가 연산하기 쉬운 이유에 대해서는 다음 섹션에서 이진 트리의 속성에서 자세히 설명하겠습니다. 모든 트리 구조는 특정 정규 변형을 통해 이진 트리로 변환될 수 있습니다.

또한 다이어그램을 사용하여 이진 트리가 무엇인지 보여줍니다.

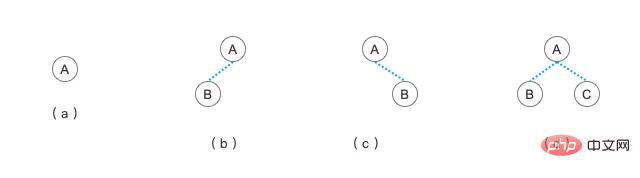
이진 트리에서 왼쪽 자식 노드와 그 자손은 현재 노드의 왼쪽 하위 트리로 간주될 수 있습니다. 오른쪽 노드와 그 하위 노드도 현재 노드의 오른쪽 하위 트리로 간주될 수 있습니다. 노드의 자식 노드에 따라 위 그림과 같이 여러 가지 이진 트리 형태가 있습니다.

• (a) 트리는 노드가 하나뿐인 트리입니다. 노드가 하나뿐인 이진 트리라고도 할 수 있습니다.

• (b) 트리는 왼쪽 노드가 하나만 있는 이진 트리입니다

• ( c) 트리는 오른쪽 노드가 하나만 있는 이진 트리입니다.

• (d) 트리는 왼쪽과 오른쪽 노드가 두 개인 이진 트리입니다.

이진 트리의 속성

속성 1: 이진 트리의 i번째 수준에는 최대 2i-1개의 노드가 있습니다(i >= 1)

속성 2: 깊이 k인 이진 트리에는 최대 2k - 1개의 노드가 있습니다(k >= 1)

속성 3: 임의의 이진 트리 T에 대해 최종 노드 수가 n0이고 차수가 2인 노드 수가 n2인 경우 n0 = n2 + 1

속성 4: 완전한 이진의 깊이 n 노드가 있는 트리는 log2n + 1

속성 5: n 노드(깊이는 log2n + 1)가 있는 완전한 이진 트리의 노드가 레이어 순서(첫 번째 수준에서 log2n + 1번째 수준까지)로 번호가 매겨지면 각 노드는 왼쪽에서 오른쪽으로) 모든 A 노드 i(1

1. i = 1이면 노드 i는 이진 트리의 루트이고 부모가 없습니다. i > 1이면 해당 부모는 노드 i/2
2. 입니다. 2i > n이면 노드 i에는 왼쪽 자식이 없습니다(노드 i는 리프 노드입니다). 그렇지 않으면 왼쪽 자식은 노드 2i
3. 입니다. 2i + 1 > n이면 노드 i에는 오른쪽 자식이 없습니다. 그렇지 않으면 오른쪽 자식은 노드 2i + 1

결국 이진 트리의 5가지 속성에 대한 자세한 내용은 다루지 않겠습니다. 우리 기사 시리즈의 목적은 또한 간단한 예를 사용하는 것입니다. 증거를 도출하기 위해 간단하고 조잡하게 수학 공식을 사용하는 대신 모든 사람이 데이터 구조와 알고리즘의 본질을 배울 수 있도록 하여 그림에서 계산할 수 있습니다.

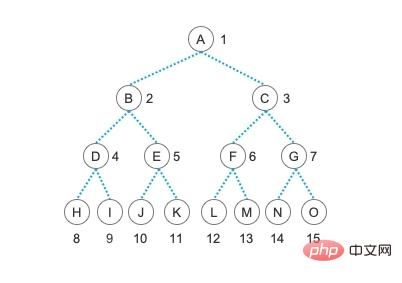
• 속성 1의 경우 공식에 따르면 현재 이진 트리는 세 번째 수준, 즉 4개 노드에서 최대 23-1개의 노드만 가질 수 있습니다. 4번째 레이어에는 최대 24-1만 있을 수 있으며, 이는 23 = 8개의 노드입니다. 속성 2의 경우 현재 그림의 트리 깊이는 4이며 이는 최대 24-1 = 15가 있음을 의미합니다. 노드

• 에는 속성 3이 있으므로 먼저 차수가 2인 노드 수를 계산합니다. 이 그림에는 차수가 2인 7개의 노드, 즉 A, B, C, D, E, F, G, 네 번째 레이어의 노드에는 하위 노드가 없습니다. 즉, 모두 0도이며, 터미널 노드(리프 노드)라고도 합니다. 이제 n2 = 7. 속성 공식에 따르면 n0 = n2 + 1 = 7 + 1 = 8

• 을 얻을 수 있습니다. 그래프의 노드 수는 15입니다. 속성 4의 공식을 적용하면 log2n을 얻을 수 있습니다. + 1 = log215 + 1 = 3.91(반내림) + 1 = 3 + 1 = 4, 현재 트리의 깊이는 4, 속성 4와 속성 2는 상보적인 것으로 간주될 수 있습니다.

• 속성 5의 경우 주의하세요. 각 노드의 가장자리에 있는 숫자의 경우 E 노드를 예로 선택합니다. E 노드는 현재 5이므로 해당 부모는 5/2 = 2(내림)입니다. E의 왼쪽 자식은 2i, 즉 2*5=10이고 E의 오른쪽 자식은 2i + 1입니다. is 2*5+1 = 11; 속성 5의 정의는 더 추상적이며 리프 노드를 사용하여 설명하고 전체 이진 트리를 목표로 하지만 실제로 의미는 여기서 설명하는 것과 동일합니다. 다른 노드에서 이를 확인할 수 있습니다. 속성 5는 나중에 이야기할 이진 트리를 저장하기 위해 순차 구조를 사용하는 데 매우 중요합니다!

• 이진 트리의 다섯 가지 속성과 그 의미를 꼭 숙지하고 기억하세요. 이후 연구에서는 이진 트리의 순서, 연결된 저장 구조, 이진 트리 순회 등의 문제에 부딪힐 수 있기 때문입니다. 다섯 가지 속성에 대한 내용을 문의하세요. 이진트리 학습에 있어서 가장 기본적인 영혼이라고 할 수 있다.

  숲

  마지막으로 '숲'이 무엇인지 간략하게 알아보겠습니다. 여러 그루의 나무가 모여 '숲'을 이룬다. 위 이진트리의 설명도처럼 (a)(b)(c)(d)를 모아서 전체적으로 보면 "숲"이고, 이 "숲" 안에는 (a)가 있다 (b) (c) (d) 이 네 그루의 나무들.

  숲 속의 나무들 사이에는 아무런 연관성이 없습니다. 숲을 운영하거나 횡단하려면 숲을 나무로 바꾸는 경우가 많습니다. 특정 알고리즘과 단계는 우리 연구의 초점이 아니므로 누구나 이해할 수 있습니다. 깊이 있게 공부하고 싶은 학생들은 관련 콘텐츠를 검색하거나 관련 교과서를 참고할 수 있습니다.

  요약

  더미와 큐부터 나무 뒤까지, 갑자기 큰 발걸음을 내디뎠다는 느낌이 드시나요? 조금 혼란 스럽습니까? 상관없습니다. 오늘 내용은 사실 기본적인 이론 내용입니다. 이해할 수 있으면 이해하고, 계속 공부한 다음 오늘 다시 와서 개념을 살펴보세요.

  학습은 계속해서 발전하는 과정을 반복하는 것은 아닙니다. 물론 모든 것이 기초에 기초해야 합니다. 트리의 데이터 구조와 몇 가지 간단한 순회 알고리즘을 이해한 후에는 다시 이러한 개념을 깊이 이해하고 암기하세요. 일반 인터뷰에서 트리 관련 질문은 문제가 되지 않을 것이라고 믿습니다.

  추천 학습: php 비디오 튜토리얼

위 내용은 3분 안에 트리와 이진 트리에 대해 알아보세요의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!