이진 트리와 유사한 그래프의 너비 우선 순회는 무엇입니까?
- 青灯夜游원래의
- 2020-08-29 16:44:3222661검색
그래프의 너비 우선 순회는 이진 트리의 레이어별 순회와 유사한 수평 우선 순회입니다. 너비 우선 순회는 루트 노드부터 시작하여 트리의 너비를 따라 순회합니다. 즉, 계층적 방식으로 순회합니다. 각 계층은 위에서 아래로, 각 계층에서는 왼쪽에서 오른쪽(또는 오른쪽으로)으로 순차적으로 방문됩니다. 왼쪽) 노드에 접근하려면 한 레벨을 방문한 후 더 이상 접근할 수 없는 노드가 있을 때까지 다음 레벨로 진입해야 합니다.

1. 소개
그래프 순회도 트리 순회와 마찬가지로 그래프의 특정 지점에서 시작하여 특정 방법에 따라 그래프의 모든 정점을 방문하며 한 번만 방문합니다.
하지만 그래프 순회는 트리보다 더 복잡합니다. 그래프의 모든 정점은 다른 정점과 인접할 수 있으므로 그래프 순회 중에 방문한 정점을 기록하여 반복 방문을 방지해야 합니다.
다양한 검색 경로에 따라 그래프 순회 방법을 너비 우선 검색과 깊이 우선 검색의 두 가지 유형으로 나눌 수 있습니다.
2. 그래프의 기본 개념
2.1. 무방향 그래프와 무방향 그래프
꼭짓점 쌍(u, v)은 순서가 없습니다. 즉, (u, v)와 (v, u)는 동일한 모서리입니다. 일반적으로 한 쌍의 괄호로 표현됩니다.
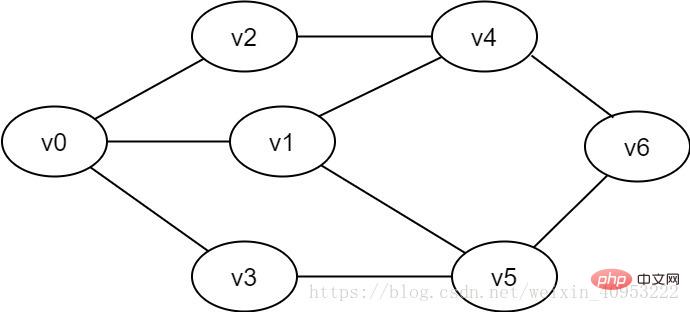
그림 2-1-1 무방향 그래프의 예
정점 쌍
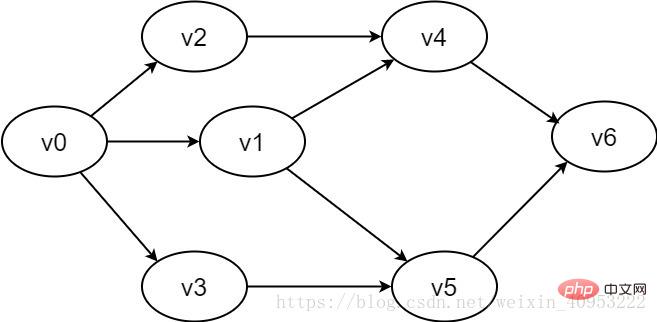
그림 2-1-2 유향 그래프의 예
2.2 Quanhe Net
그래프의 각 가장자리에는 다음과 같은 의미를 갖는 값이 있을 수 있습니다. 가치가 바로 그 가장자리에 있습니다. 이러한 종류의 가중치 그래프를 네트워크라고 합니다.
2.3. 연결된 그래프와 연결되지 않은 그래프
연결된 그래프: 무방향 그래프 G에서 꼭지점 v에서 꼭지점 v'까지의 경로가 있으면 v와 v'는 연결되어 있다고 합니다. 그래프의 임의의 두 꼭지점 v, v'∈V, v와 v'가 연결되면 G는 연결 그래프라고 합니다. 위의 두 그래프는 모두 연결된 그래프입니다.
연결 끊김 그래프: 무방향 그래프 G에서 v와 v' 사이에 연결 끊김이 있으면 G를 연결 끊김 그래프라고 합니다.
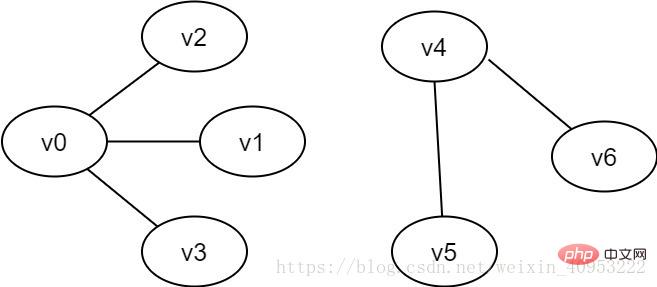
그림 2-3 연결되지 않은 그래프의 예
3. 너비 우선 검색
3.1 알고리즘의 기본 아이디어
트리의 계층적 순회 과정. 큐를 사용하여 구현해야 합니다. 그림 2-1-1과 같이 v0에서 v6까지 모든 정점을 순회하려면 v0을 첫 번째 레이어로 설정하고 v1, v2, v3을 두 번째 레이어로 설정하고 v4와 v5를 세 번째 레이어로 설정하면 됩니다. v6 네 번째 레이어의 경우 각 레이어의 각 꼭지점을 하나씩 통과합니다.
구체적인 과정은 다음과 같습니다.
1. 준비: 방문한 정점을 기록하기 위한 방문 배열을 생성하고, 각 레이어의 정점을 저장하기 위한 큐를 생성합니다.
2. 그림의 v0부터 방문을 시작하고 Visited[v0] 배열의 값을 true로 설정한 후 대기열에 v0을 추가합니다.
3. 대기열이 비어 있지 않은 한 다음 작업을 반복하십시오.
(1) 대기열을 종료하려면 팀 상단의 u를 클릭하세요.
(2) u의 인접한 모든 정점 w를 차례로 확인합니다. Visit[w] 값이 false이면 w를 방문하고 Visited[w]를 true로 설정하고 w를 대기열에 추가합니다.
3.2. 알고리즘 구현 과정
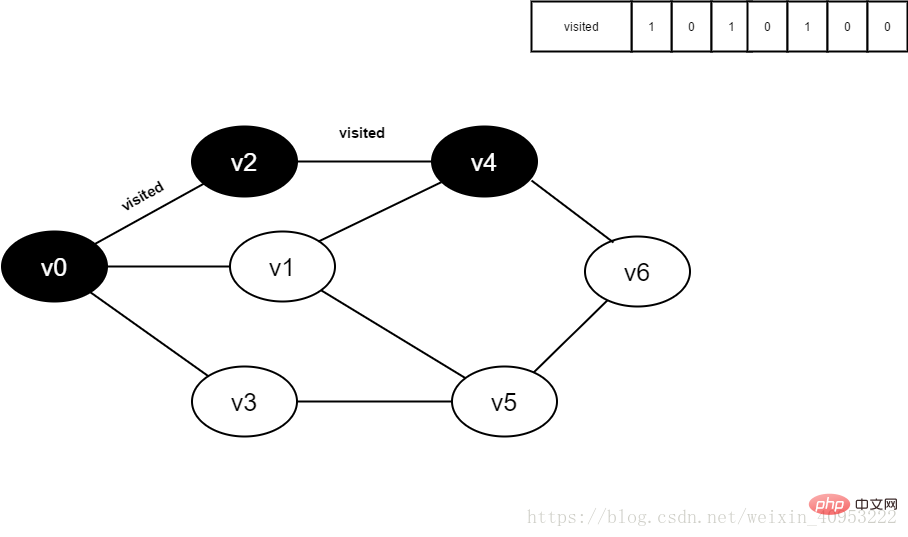
흰색은 방문하지 않았음을 나타내고, 회색은 방문 예정임을 나타내고, 검은색은 방문했음을 나타냅니다.
visited 배열: 0은 방문하지 않았음을 의미하고, 1은 방문했음을 의미합니다.
큐: 요소는 큐의 선두에서 나오고 요소는 꼬리에서 들어옵니다.
1. 처음에는 모든 정점을 방문하지 않았고 방문한 배열은 0으로 초기화되었으며 대기열에 요소가 없습니다.
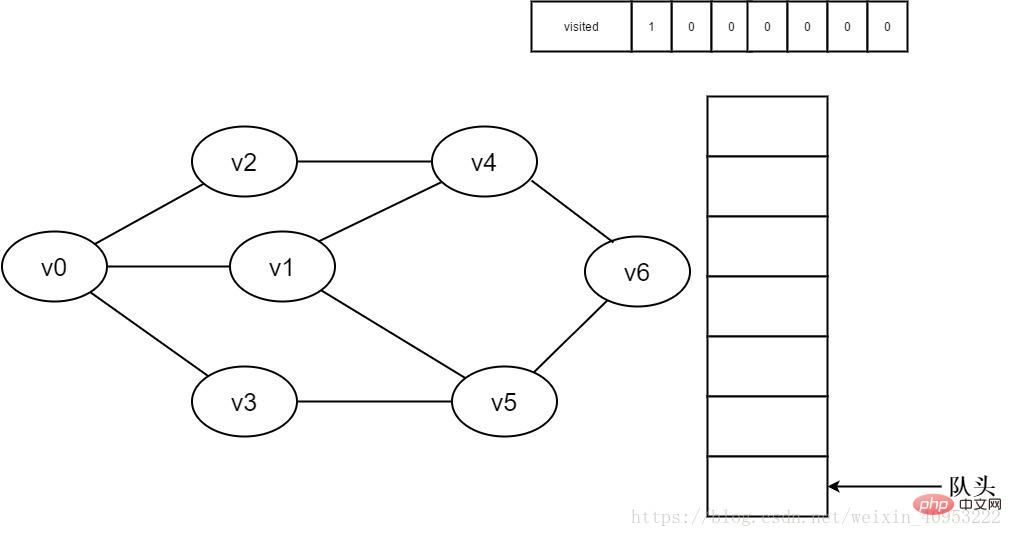
그림 3-2-1
2.
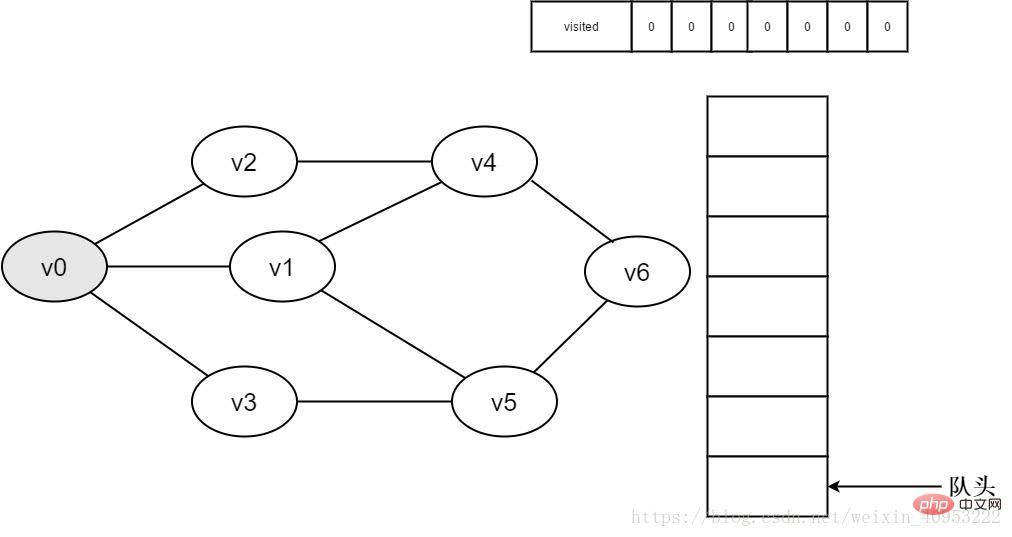
그림 3-2-2
3. 정점 v0을 방문하고, Visited[0]의 값을 1로 설정하고, 대기열에 v0을 추가합니다.
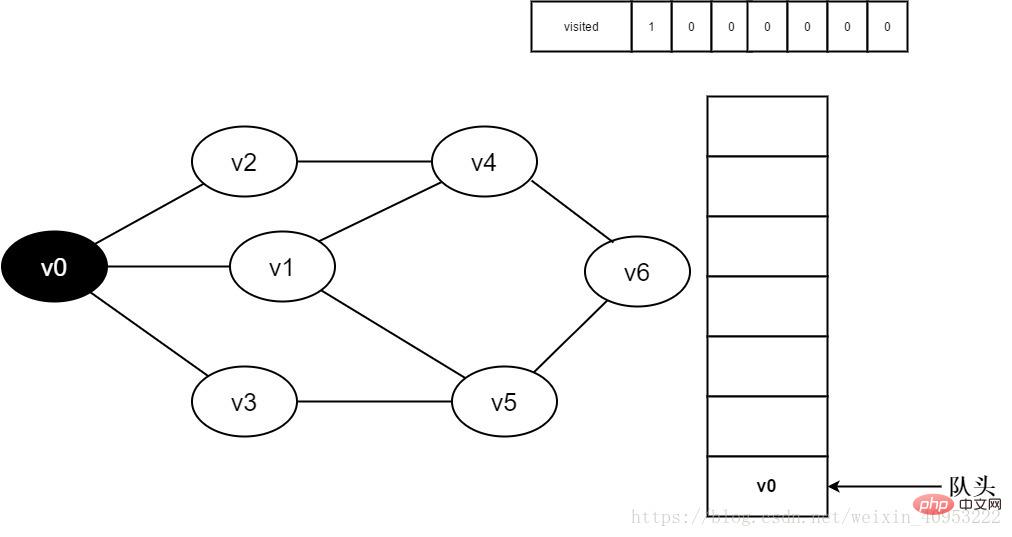
사진 3-2-3
4. v0을 큐에서 제거하고 v0의 인접 지점 v2를 방문합니다. Visited[2]를 결정합니다. Visited[2]의 값이 0이므로 v2를 방문합니다.
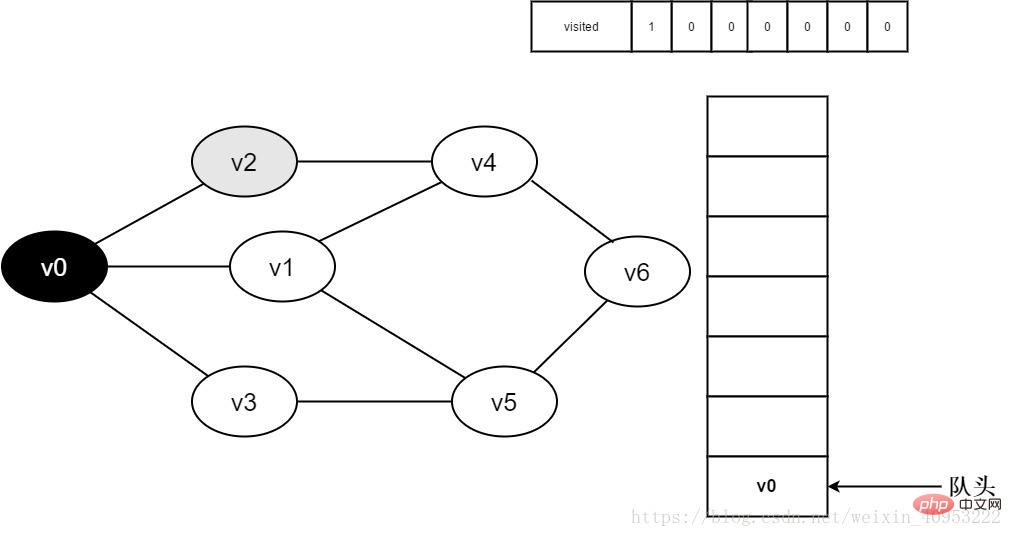
그림 3-2-4
5. Visit[2]를 1로 설정하고 대기열에 v2를 추가합니다.
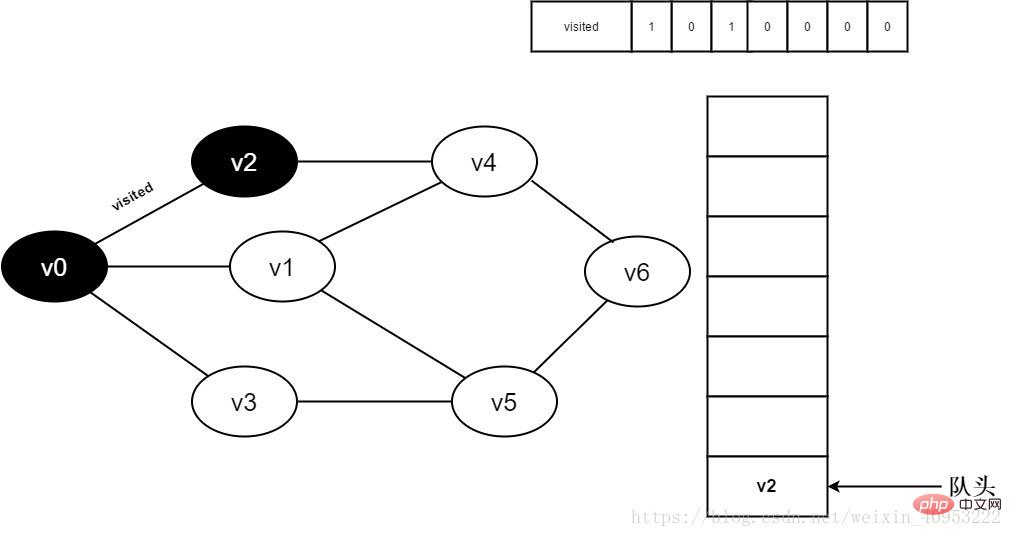
그림 3-2-5
6. v0 인접 지점 v1을 방문합니다. Visited[1]의 값이 0이므로 Visited[1]을 확인하고 v1을 방문합니다.
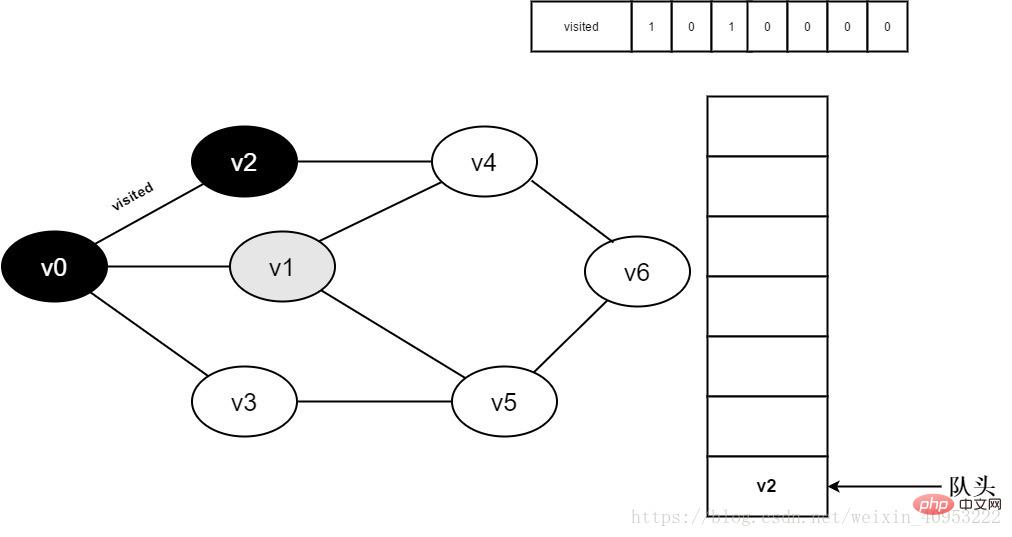
그림 3-2-6
7. Visit[1]을 0으로 설정하고 대기열에 v1을 추가합니다.
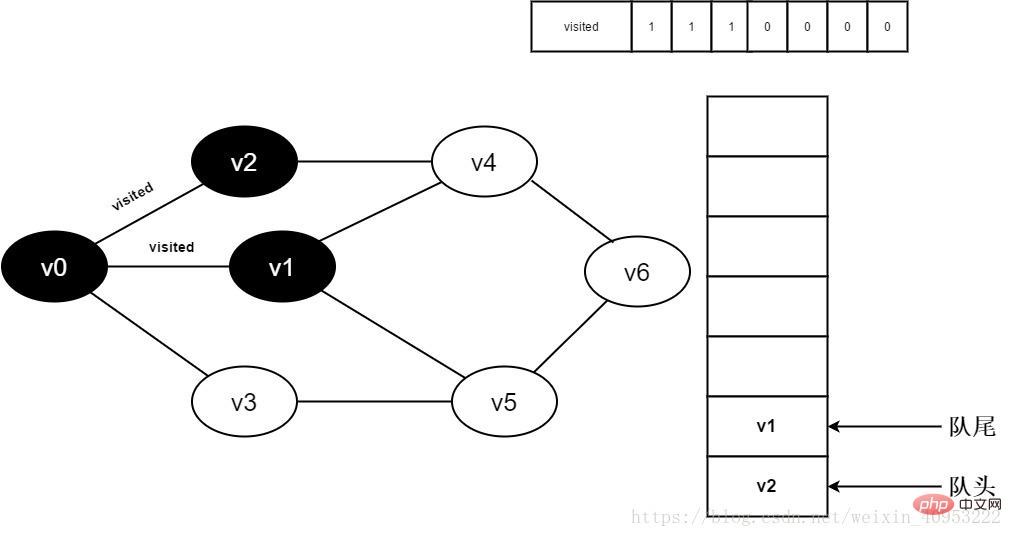
그림 3-2-7
8. 판사가 [3]을 방문했습니다. 값이 0이므로 v3을 방문하세요. Visited[3]를 0으로 설정하고 v3을 대기열에 추가합니다.
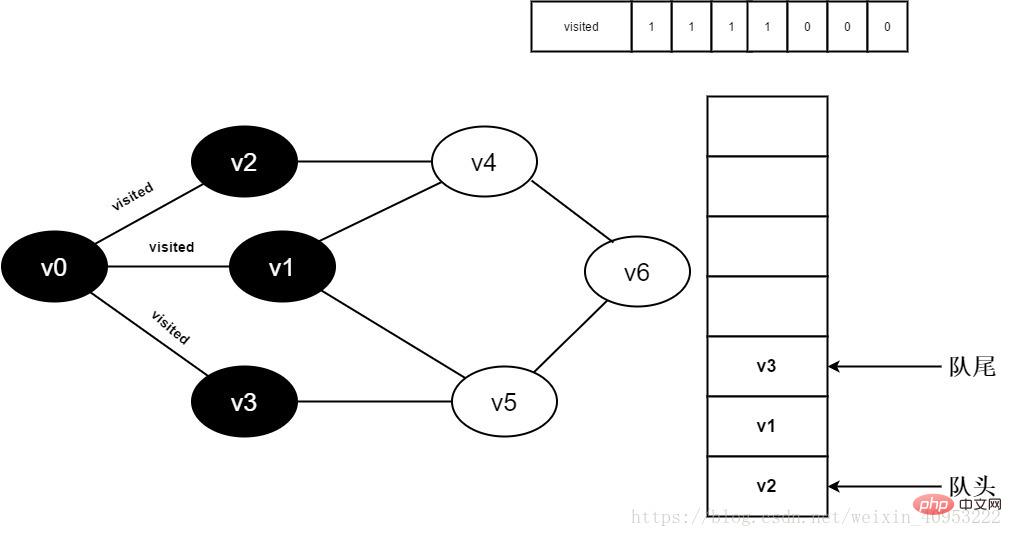
그림 3-2-8
9.v0의 모든 인접 지점을 방문했습니다. 헤드 요소 v2를 대기열에서 빼고 v2의 모든 인접한 지점을 방문하기 시작합니다.
v2 인접 포인트 v0 방문을 시작하고 심사위원이 [0]을 방문했는데 값이 1이므로 방문이 수행되지 않습니다.
v2 인접 지점 v4를 계속 방문하여 방문[4]을 결정합니다. 값이 0이므로 v4를 방문합니다.
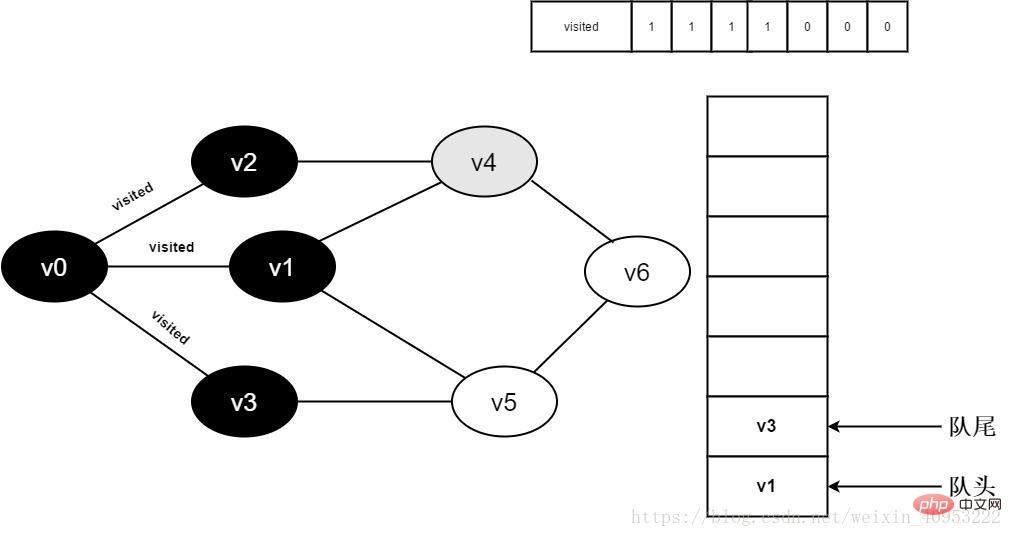
그림 3-2-9
10. 4] 1로 설정하고 v4를 대기열에 추가합니다.

그림 3-2-10
11.v2의 모든 인접 지점을 방문했습니다. 헤드 요소 v1을 큐에서 제거하고 v1의 모든 인접한 지점을 방문하기 시작합니다.
v1 인접 포인트 v0 방문을 시작합니다. Visited[0] 값이 1이므로 방문이 수행되지 않습니다.
v1 인접 포인트 v4를 계속 방문합니다. Visited[4]의 값이 1이므로 방문이 수행되지 않습니다.
v1 인접 포인트 v5를 계속 방문합니다. 왜냐하면 Visited[5] 값이 0이기 때문입니다. 아래와 같이 v5를 방문합니다.

그림 3-2-11
12 1 , 팀에 v5를 추가합니다.
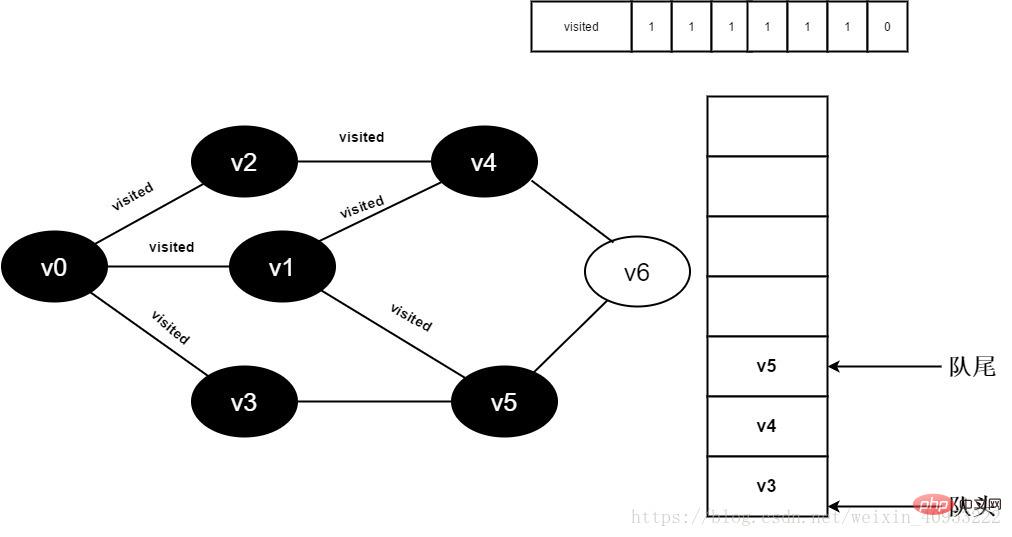
그림 3-2-12
13.v1의 모든 인접 포인트를 방문하고 v3의 헤드 요소를 대기열에서 제거하고 v3의 모든 인접 포인트에 액세스하기 시작합니다.
v3 이웃 포인트 v0 방문을 시작합니다. Visited[0] 값이 1이므로 방문이 수행되지 않습니다.
v3 이웃 포인트 v5를 계속 방문합니다. Visited[5] 값이 1이므로 방문이 수행되지 않습니다.
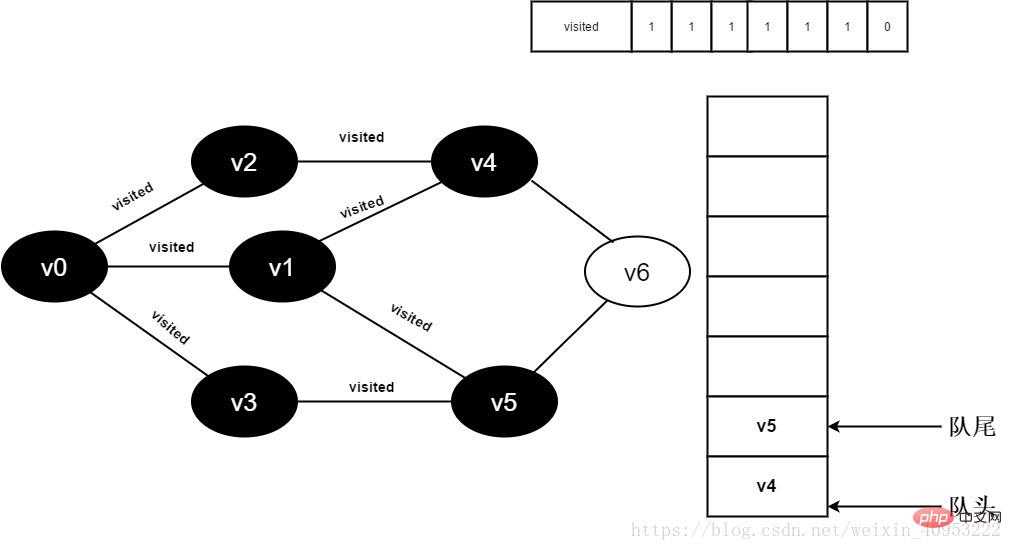
그림 3-2-13
14.v3의 모든 인접 지점을 방문했습니다. v4의 헤드 요소가 대기열에서 제거되고 v4의 모든 인접 지점이 방문되기 시작합니다.
v4의 인접 지점 v2를 방문하기 시작합니다. Visited[2]의 값이 1이므로 방문이 수행되지 않습니다.
visited[6]의 값이 0이므로 v4의 인접 지점 v6을 계속 방문합니다. 아래와 같이 v6을 방문합니다.
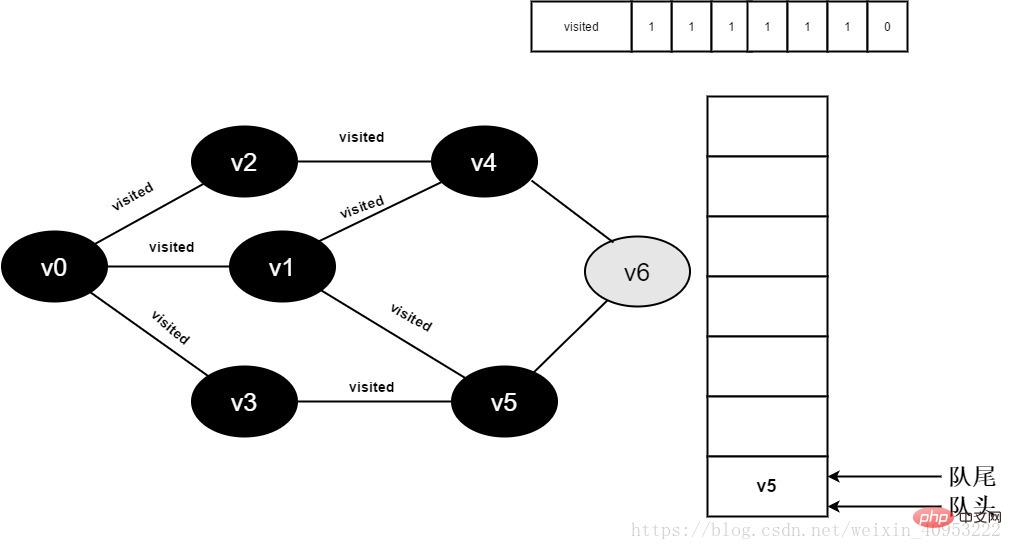
그림 3-2-14
15. Visited[6]의 값은 1이고 v6을 대기열에 추가합니다.
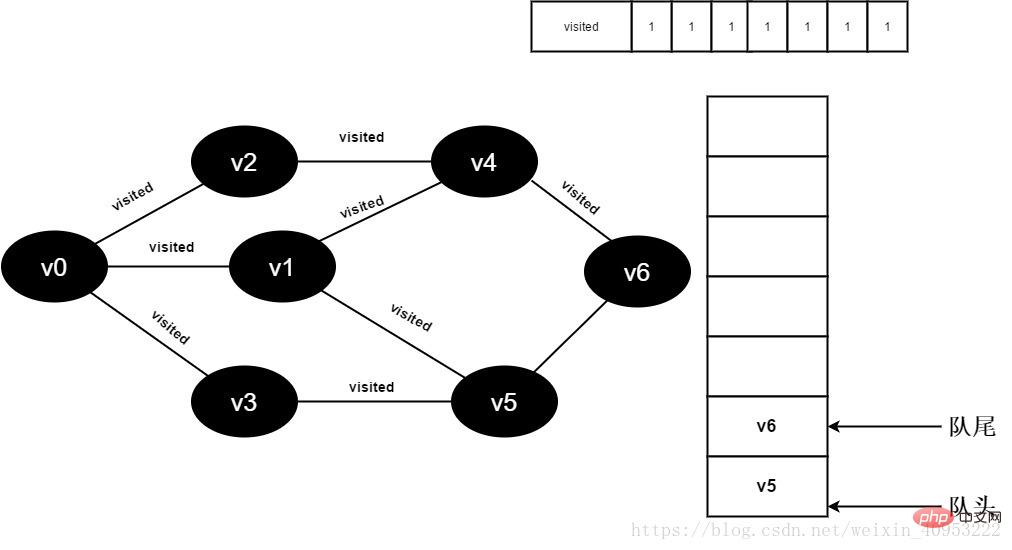
그림 3-2-15
16.v4의 모든 인접 지점이 방문되었습니다. v5의 헤드 요소가 대기열에서 제거되고 v5의 모든 인접 지점이 방문되기 시작합니다.
v5 이웃 포인트 v3 방문을 시작합니다. Visited[3]의 값이 1이므로 방문이 수행되지 않습니다.
v5 이웃 포인트 v6을 계속 방문하세요. Visited[6]의 값이 1이므로 방문이 수행되지 않습니다.
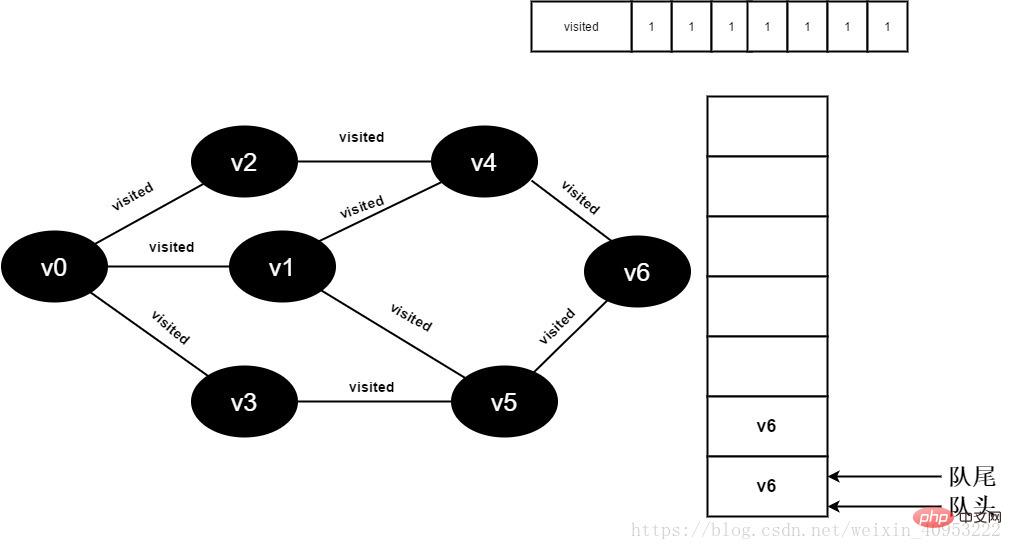
그림 3-2-16
17.v5의 모든 인접 지점을 방문했으며 v6의 헤드 요소를 대기열에서 제외하고 v6의 모든 인접 지점에 액세스하기 시작합니다.
v6 이웃 포인트 v4 방문을 시작합니다. Visited[4]의 값이 1이므로 방문이 수행되지 않습니다.
visited[5]의 값이 1이므로 방문이 수행되지 않으므로 v6 이웃 포인트 v5를 계속 방문합니다.
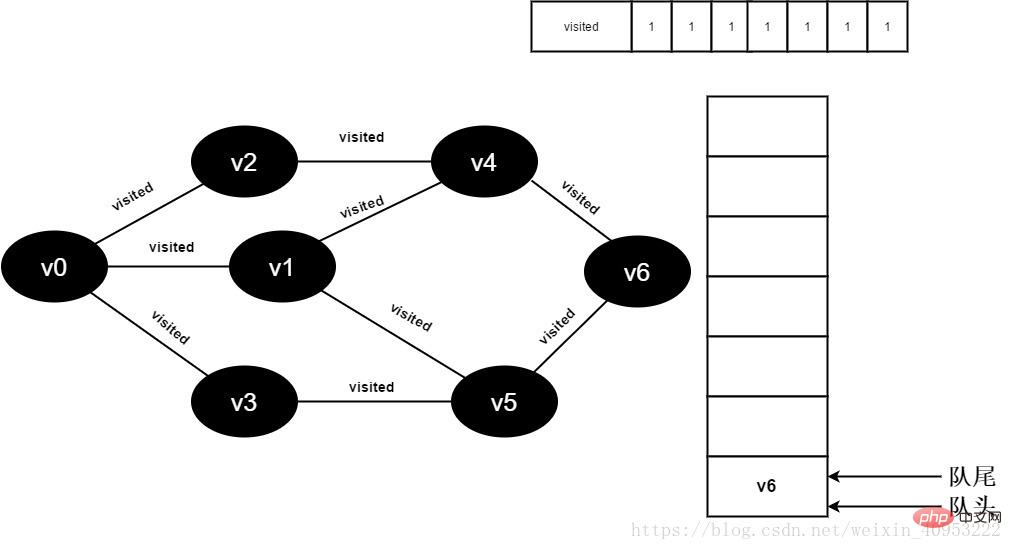
그림 3-2-17
18. 큐는 비어 있고 루프를 종료하며 모든 정점을 방문했습니다.

그림 3-2-18
3.3 특정 코드 구현
3.3.1 인접 행렬을 사용하여 그래프의 너비 우선 탐색을 표현합니다.
3.3.2 대표 인접 리스트를 이용한 그래프 너비 우선 탐색
/*一些量的定义*/
queue<char> q; //定义一个队列,使用库函数queue
#define MVNum 100 //表示最大顶点个数
bool visited[MVNum]; //定义一个visited数组,记录已被访问的顶点
/*邻接矩阵存储表示*/
typedef struct AMGraph
{
char vexs[MVNum]; //顶点表
int arcs[MVNum][MVNum]; //邻接矩阵
int vexnum, arcnum; //当前的顶点数和边数
}
AMGraph;
/*找到顶点v的对应下标*/
int LocateVex(AMGraph &G, char v)
{
int i;
for (i = 0; i < G.vexnum; i++)
if (G.vexs[i] == v)
return i;
}/*采用邻接矩阵表示法,创建无向图G*/
int CreateUDG_1(AMGraph &G)
{
int i, j, k;
char v1, v2;
scanf("%d%d", &G.vexnum, &G.arcnum); //输入总顶点数,总边数
getchar(); //获取'\n’,防止其对之后的字符输入造成影响
for (i = 0; i < G.vexnum; i++)
scanf("%c", &G.vexs[i]); //依次输入点的信息
for (i = 0; i < G.vexnum; i++)
for (j = 0; j < G.vexnum; j++)
G.arcs[i][j] = 0; //初始化邻接矩阵边,0表示顶点i和j之间无边
for (k = 0; k < G.arcnum; k++)
{
getchar();
scanf("%c%c", &v1, &v2); //输入一条边依附的顶点
i = LocateVex(G, v1); //找到顶点i的下标
j = LocateVex(G, v2); //找到顶点j的下标
G.arcs[i][j] = G.arcs[j][i] = 1; //1表示顶点i和j之间有边,无向图不区分方向
}
return 1;
}
3.4. 연결되지 않은 그래프의 너비 우선 탐색 구현 방법/*采用邻接矩阵表示图的广度优先遍历*/
void BFS_AM(AMGraph &G,char v0)
{
/*从v0元素开始访问图*/
int u,i,v,w;
v = LocateVex(G,v0); //找到v0对应的下标
printf("%c ", v0); //打印v0
visited[v] = 1; //顶点v0已被访问
q.push(v0); //将v0入队
while (!q.empty())
{
u = q.front(); //将队头元素u出队,开始访问u的所有邻接点
v = LocateVex(G, u); //得到顶点u的对应下标
q.pop(); //将顶点u出队
for (i = 0; i < G.vexnum; i++)
{
w = G.vexs[i];
if (G.arcs[v][i] && !visited[i])//顶点u和w间有边,且顶点w未被访问
{
printf("%c ", w); //打印顶点w
q.push(w); //将顶点w入队
visited[i] = 1; //顶点w已被访问
}
}
}
}
4. 깊이 우선 탐색4.1 알고리즘의 기본 아이디어 검색은 트리의 선주문 순회와 유사합니다. 구체적인 프로세스는 다음과 같습니다. 준비: 방문한 모든 정점을 기록하기 위한 방문 배열을 만듭니다. 1. 사진 속 v0부터 시작해서 v0을 방문하세요. 2. v0의 첫 번째 방문하지 않은 인접점을 찾아 정점을 방문합니다. 이 정점을 새 정점으로 사용하고 방금 방문한 정점에 방문하지 않은 인접 정점이 없을 때까지 이 단계를 반복합니다. 3. 아직 방문하지 않은 인접점이 있는 이전에 방문한 정점으로 돌아가서, 계속해서 방문하지 않은 정점의 다음 선행점을 방문합니다. 4. 모든 정점을 방문하고 검색이 끝날 때까지 2단계와 3단계를 반복합니다. 4.2 알고리즘 구현 과정1. 처음에는 모든 정점을 방문하지 않았으며 방문한 배열은 비어 있습니다. 
그림 4-2-1

그림 4-2-2
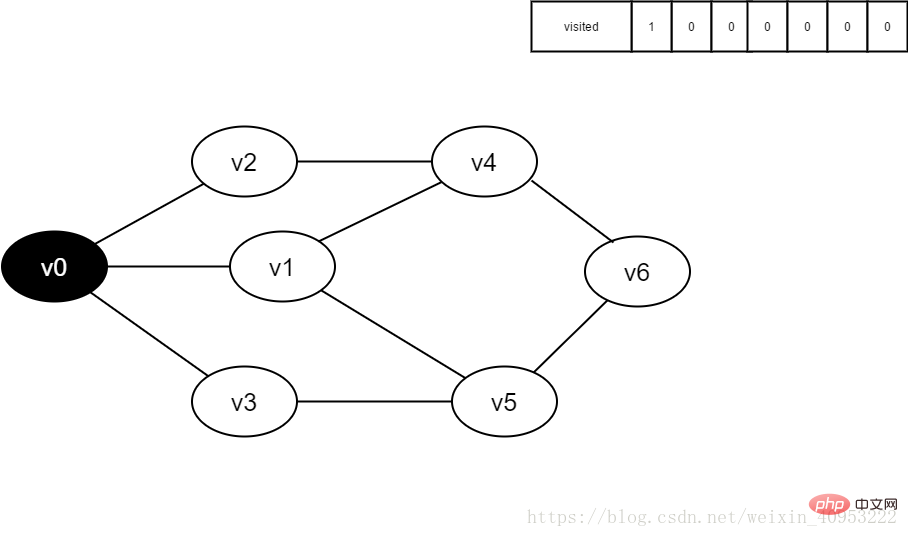
그림 4-2-3
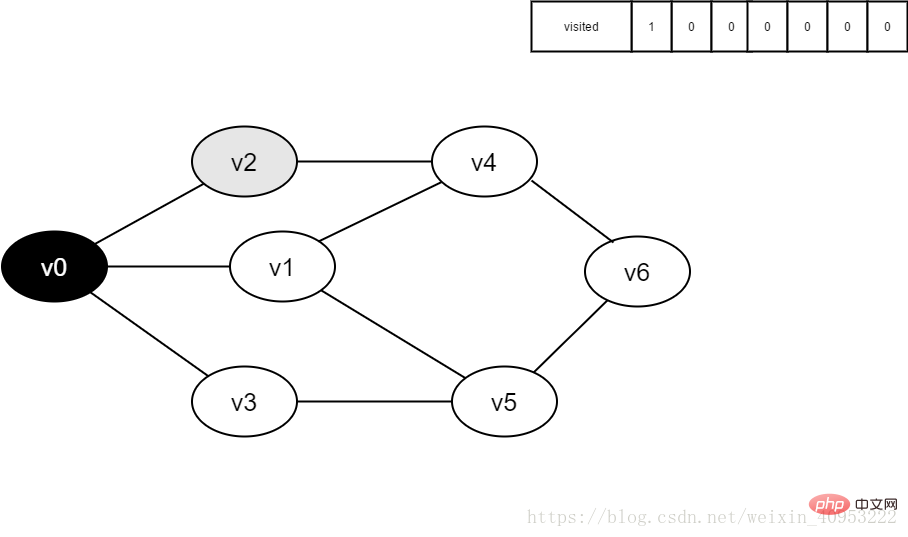
그림 4-2-4
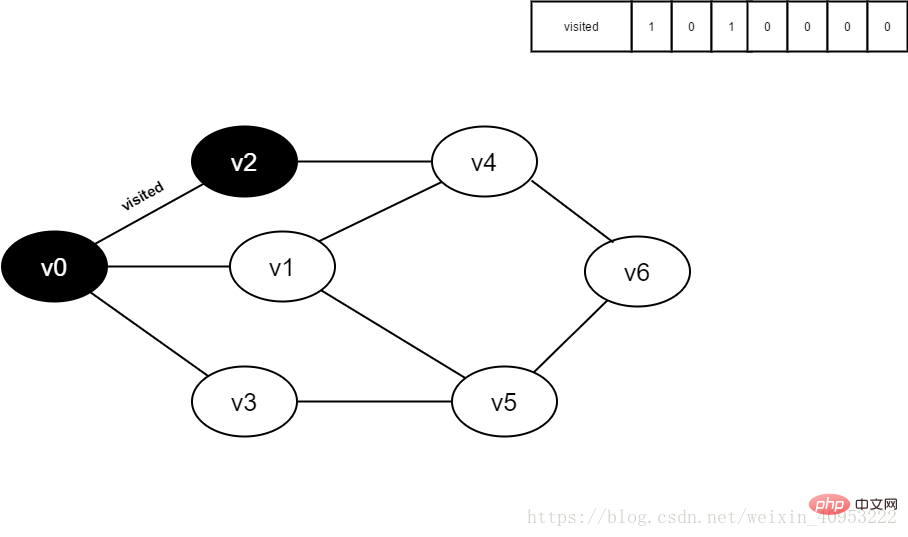
그림 4-2-5
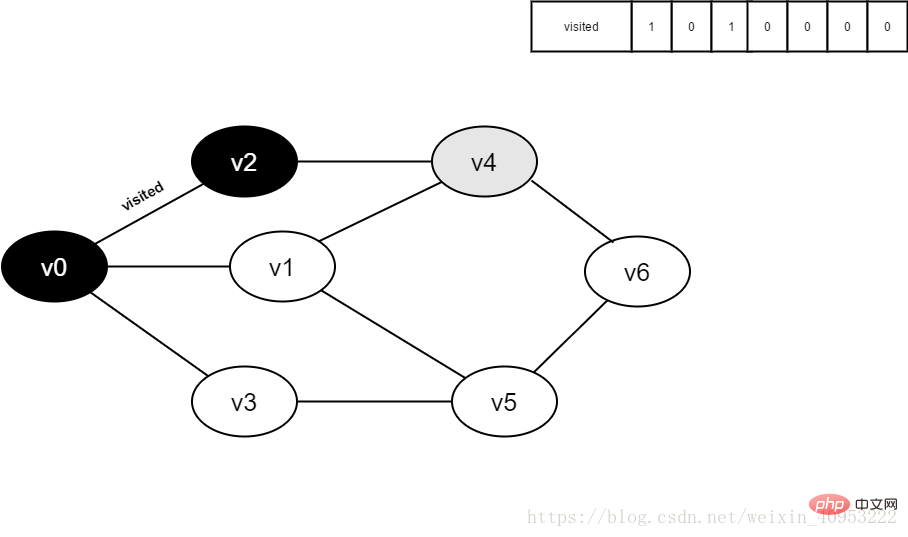
그림 4-2-6
그림 4-2-7
8. v4의 인접 지점 v1을 방문하고, 판사가 방문[1]하며, 그 값은 0이고, v1을 방문합니다.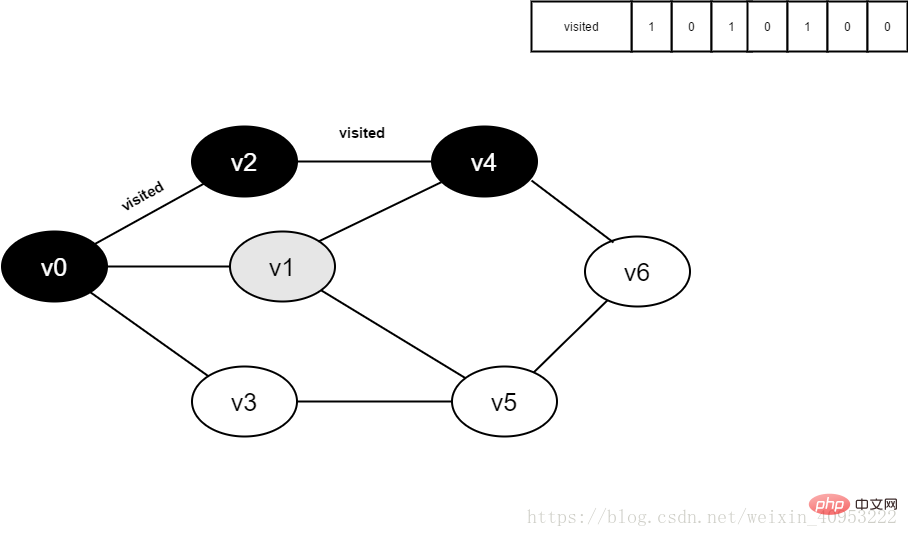
그림 4-2-8
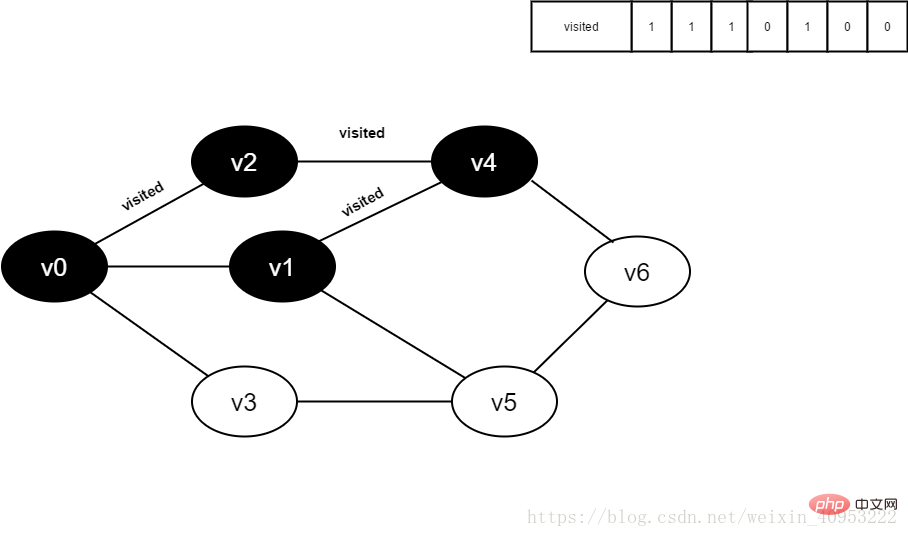
그림 4-2-9
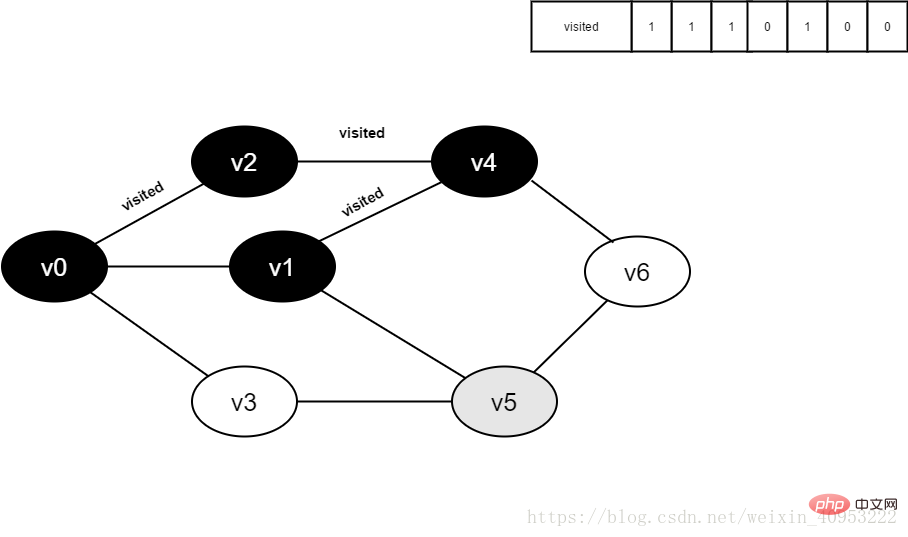
그림 4-2-10
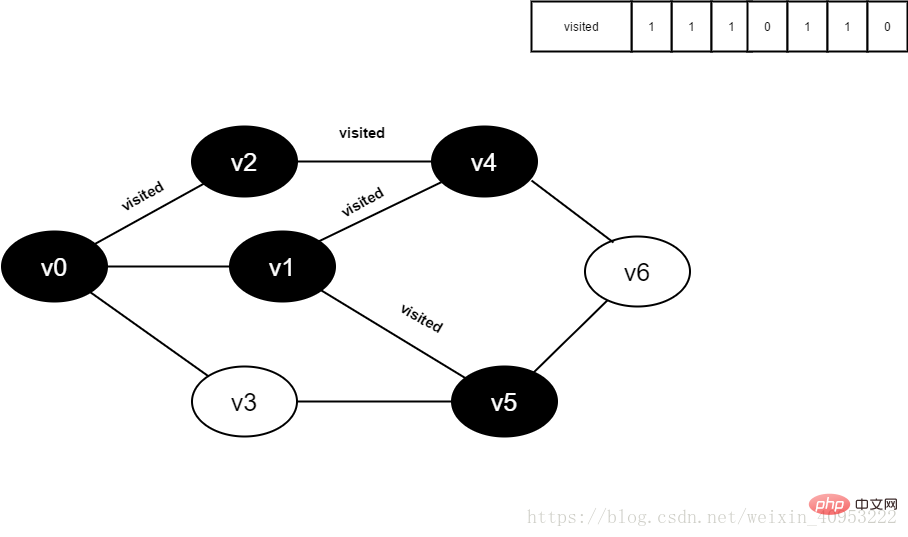
그림 4-2-11
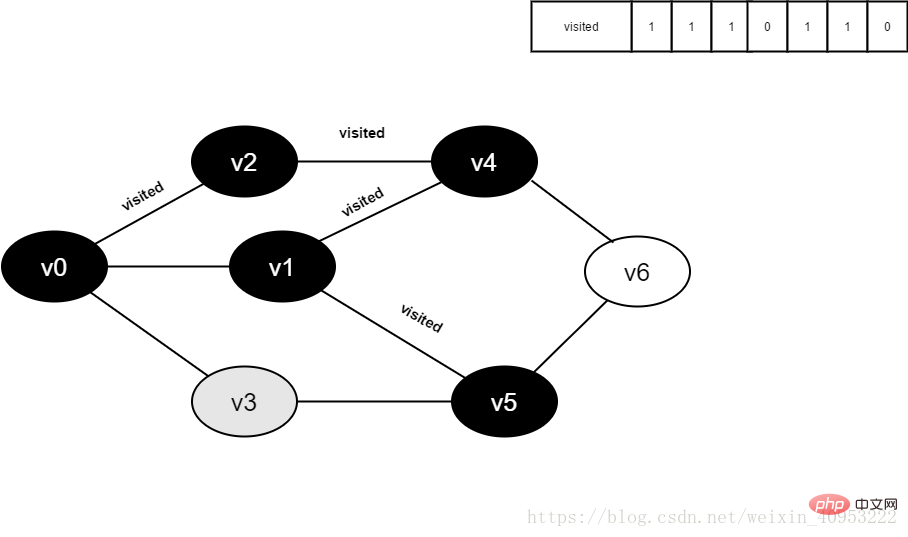
图4-2-12
13.将visited[1]置为1。
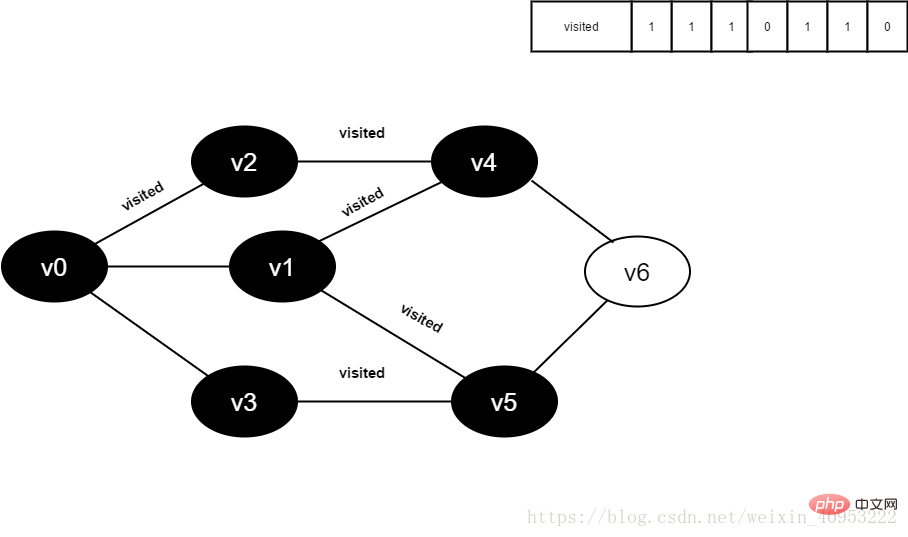
图4-2-13
14.访问v3的邻接点v0,判断visited[0],其值为1,不访问。
继续访问v3的邻接点v5,判断visited[5],其值为1,不访问。
v3所有邻接点均已被访问,回溯到其上一个顶点v5,遍历v5所有邻接点。
访问v5的邻接点v6,判断visited[6],其值为0,访问v6。
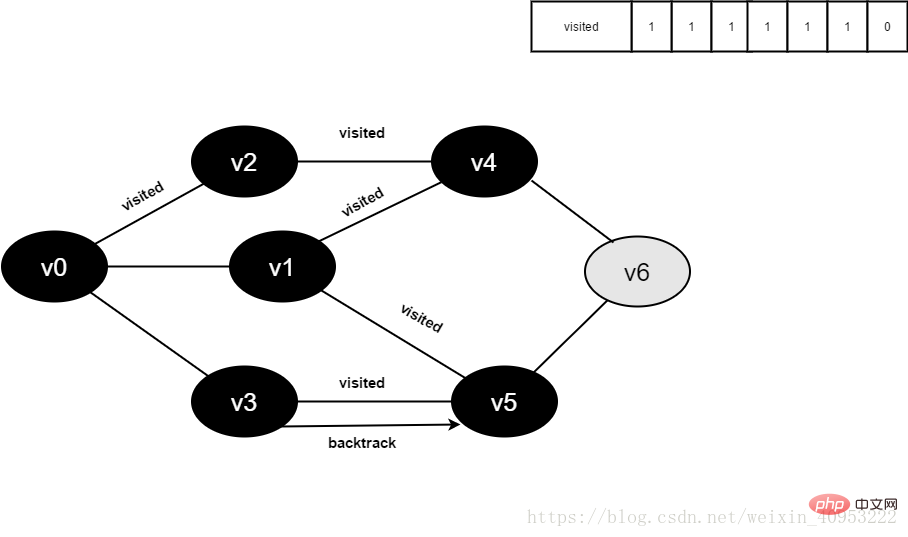
图4-2-14
15.将visited[6]置为1。
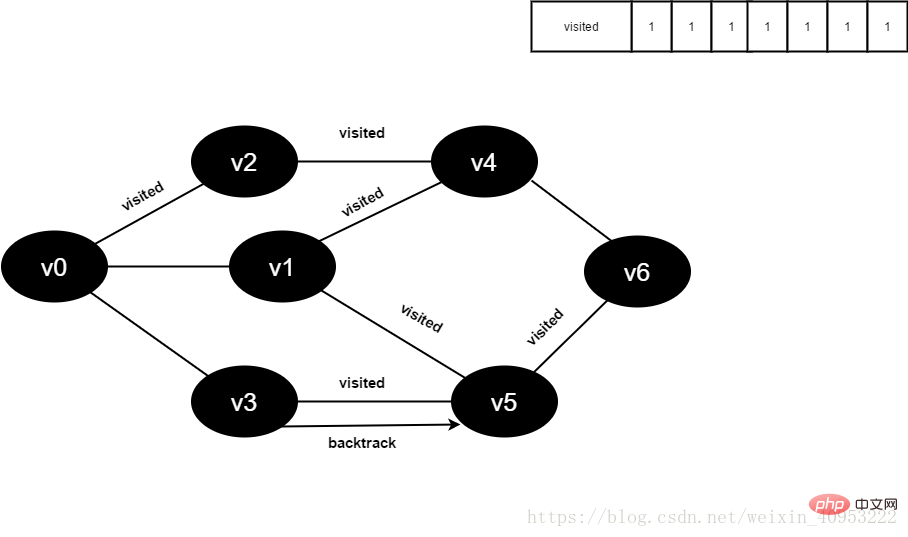
图4-2-15
16.访问v6的邻接点v4,判断visited[4],其值为1,不访问。
访问v6的邻接点v5,判断visited[5],其值为1,不访问。
v6所有邻接点均已被访问,回溯到其上一个顶点v5,遍历v5剩余邻接点。
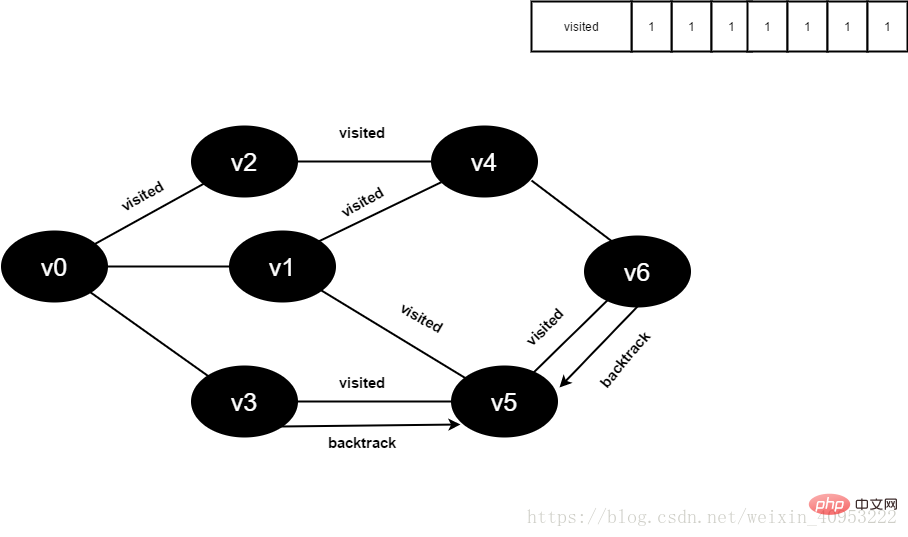
图4-2-16
17.v5所有邻接点均已被访问,回溯到其上一个顶点v1。
v1所有邻接点均已被访问,回溯到其上一个顶点v4,遍历v4剩余邻接点v6。
v4所有邻接点均已被访问,回溯到其上一个顶点v2。
v2所有邻接点均已被访问,回溯到其上一个顶点v1,遍历v1剩余邻接点v3。
v1所有邻接点均已被访问,搜索结束。
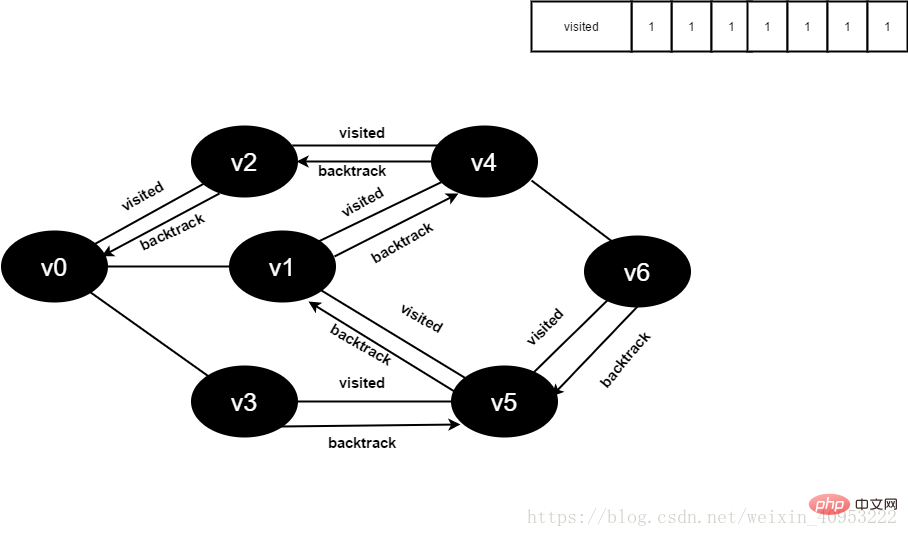
图4-2-17
4.3具体代码实现
4.3.1用邻接矩阵表示图的深度优先搜索
邻接矩阵的创建在上述已描述过,这里不再赘述
void DFS_AM(AMGraph &G, int v)
{
int w;
printf("%c ", G.vexs[v]);
visited[v] = 1;
for (w = 0; w < G.vexnum; w++)
if (G.arcs[v][w]&&!visited[w]) //递归调用
DFS_AM(G,w);
}4.3.2用邻接表表示图的深度优先搜素
邻接表的创建在上述已描述过,这里不再赘述。
void DFS_AL(ALGraph &G, int v)
{
int w;
printf("%c ", G.vertices[v].data);
visited[v] = 1;
ArcNode *p = new ArcNode;
p = G.vertices[v].firstarc;
while (p)
{
w = p->adjvex;
if (!visited[w]) DFS_AL(G, w);
p = p->nextarc;
}
}
更多相关知识,请访问:PHP中文网!
위 내용은 이진 트리와 유사한 그래프의 너비 우선 순회는 무엇입니까?의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!