Python으로 편미분 방정식을 풀 수 있나요?
- 爱喝马黛茶的安东尼원래의
- 2019-06-18 15:43:019165검색
fipy
Fick의 법칙은 거시적 혼합에 의존하지 않고 물질 전달 현상이 발생할 때 분자 확산 과정에서 물질 전달 유속과 농도 구배의 관계를 설명하는 법칙을 말합니다. Fick의 법칙은 1855년 Adolf Fick에 의해 제안되었습니다.

동적 확산의 편미분 방정식은 Fick의 제2법칙에서 구할 수 있습니다. 풀면 농도 분포와 유출 곡선을 얻을 수 있습니다.
이 문제에 대한 분석적 해결책이 있는지는 잘 모르겠지만, 수치적 해결책이 더 일반적인 해결책입니다.
fipy는 아직까지 살아 있는 희귀한 PDE 해결 Python 패키지입니다. 저자는 공식 예제를 기반으로 이 프로그램을 적용했습니다.
관련 권장 사항: "python 비디오 튜토리얼"
Problem
2차원 평판, 상단은 섭씨 1도(100은 괜찮습니다. 계수일 뿐), 나머지 세 모서리는 섭씨 0도입니다. , 전체 보드는 초기 순간에 섭씨 0도이며, 시간이 지남에 따라 열이 플레이트에 전달되어 최종적으로 평형 상태에 도달하는 것뿐만 아니라 온도가 어떻게 변화하는지 알고 싶습니다. 시간에 따라 변합니다. 열의 전달은 미분방정식으로 표현되는데, 이는 온도가 가장 빨리 낮아지는 방향으로 열이 전달되는 것으로 간단히 이해할 수 있다.
식의 오른쪽은 온도의 구배이고, 왼쪽은 시간에 따른 온도의 변화입니다.
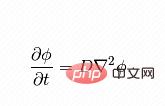
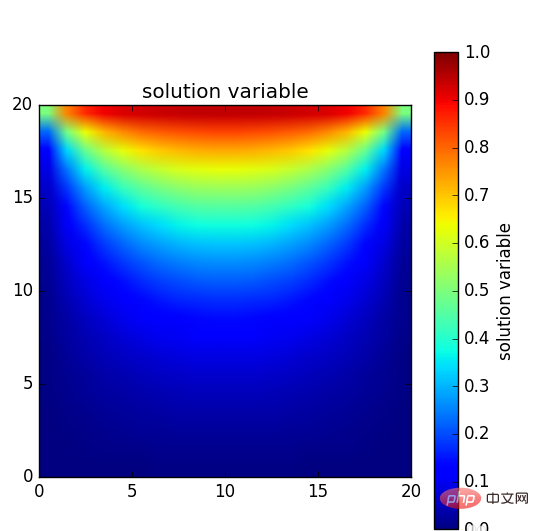
결국 보드 전체의 온도 분포는 어떻게 될까요?
 패키지 하나만 가져오면 됩니다
패키지 하나만 가져오면 됩니다
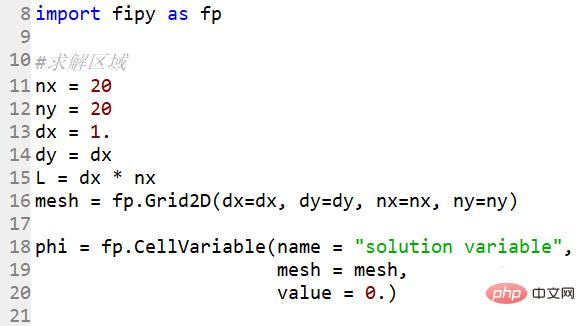
import fipy as fpOK 해결 영역, 20*20 그리드 포인트
# 해결 영역 nx = 20ny = 20dx = 1.dy = dxL = dx * nxmesh = fp.Grid2D (dx=dx, dy=dy, nx=nx, ny= ny)
phi = fp.CellVariable(이름 = "솔루션 변수", >그림 만들기
Solve
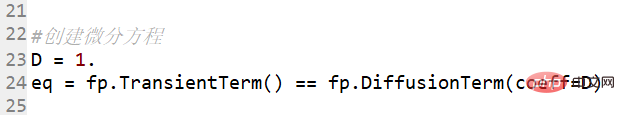
spyder의 ipython에서는요. 마지막 사진만 있어요
위 내용은 Python으로 편미분 방정식을 풀 수 있나요?의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!

