데이터 구조: 그래프와 트리의 차이점은 무엇입니까

차트와 트리는 모두 가장 일반적인 비선형 데이터 구조인데, 둘 사이의 차이점은 무엇인가요? 다음 글에서는 차트와 트리의 차이점을 설명하겠습니다. 모든 사람에게 도움이 되기를 바랍니다.

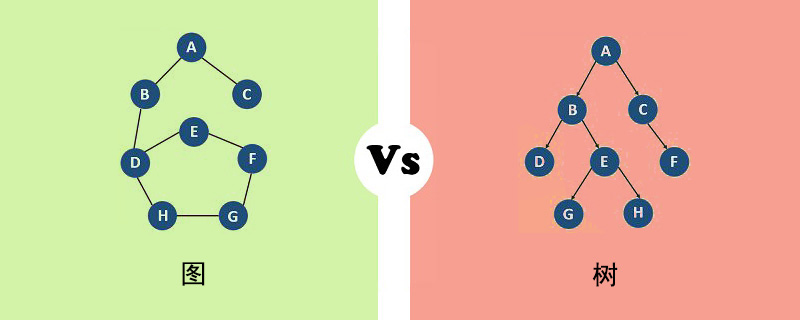
그래프

그래프는 두 세트 V와 E로 구성됩니다. 여기서 V는 비어 있지 않은 유한 정점 집합이고 E는 비어 있지 않은 유한 모서리 집합입니다. 여기에는 다음과 같은 속성이 있습니다.

1. 정점은 그래프의 노드를 나타내며 가장자리를 사용하여 원하는 수의 다른 정점에 연결할 수 있습니다.

2. 두 개의 인접한 꼭지점은 가장자리로 연결될 수 있으며 가장자리에는 가중치가 부여될 수도 있습니다.

3. 모든 그래프는 G = {V, E}로 표현될 수 있습니다.

예:

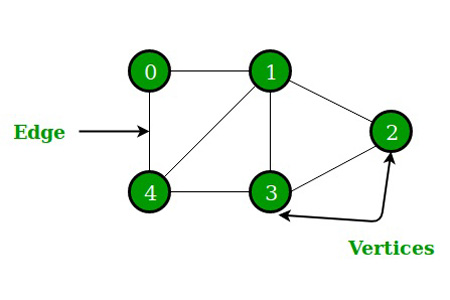
다음: G = {{V1, V2, V3, V4, V5}, {E1, E2, E3, E4, E5, E6, E7}}

Tree

트리는 n(n>0)개의 노드를 포함하는 유한 집합 K이며 다음과 같은 속성을 갖습니다.

1 트리의 루트라고 하는 트리 상단에 지정된 노드가 있습니다.

2. 나머지 데이터 항목은 하위 트리라고 불리는 분리된 하위 집합으로 나뉩니다.

3. 나무의 높이는 아래쪽으로 갈수록 늘어납니다.

4. 트리는 연결되어 있어야 합니다. 즉, 한 루트에서 다른 모든 노드까지의 경로가 있어야 합니다.

5. 루프가 포함되어 있지 않습니다.

6. 나무에는 n-1개의 면이 있습니다.

예:

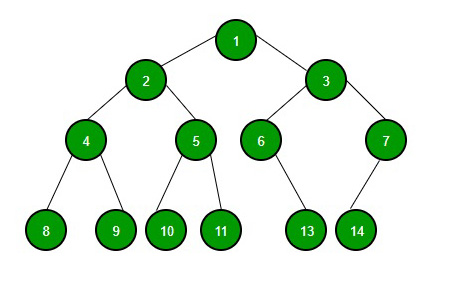
그래프와 트리의 차이점

Graphs

1. 그래프의 각 노드는 여러 개의 모서리를 가질 수 있으며 모서리는 단방향 및 양방향일 수 있습니다.

2. 차트에는 root라는 루트 노드 개념이 없습니다.

3. 그래프에는 루프와 자체 루프가 있을 수 있습니다.

4. 그래프에는 미리 정의된 모서리 수가 없으며 그래프에 따라 다릅니다.

5. 그래프는 네트워크 모델 구조입니다.

Tree

1. 일반 트리는 여러 개의 하위 노드가 있는 노드로 구성되지만 이진 트리의 경우 각 노드는 최대 2개의 하위 노드를 가질 수 있습니다. 두 노드 사이에는 단 하나의 간선만 있습니다.

2. 트리에는 루트라는 고유 노드가 있습니다.

3. 트리는 순환 또는 자체 루프를 가질 수 없습니다.

4. 트리는 n-1 모서리를 가질 수 있습니다.

5. 트리는 계층 구조입니다.

위 내용은 이 글의 전체 내용입니다. 모든 분들의 공부에 도움이 되었으면 좋겠습니다. 더 흥미로운 내용을 보려면 PHP 중국어 웹사이트의 관련 튜토리얼 열을 주의 깊게 살펴보세요! ! !

위 내용은 데이터 구조: 그래프와 트리의 차이점은 무엇입니까의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!