집 > 기사 > 백엔드 개발 > PHP 데이터 구조를 기반으로 한 재귀

PHP 데이터 구조를 기반으로 한 재귀

不言원래의: 2018-07-07 15:29:021855검색

이 기사는 주로 PHP 데이터 구조를 기반으로 재귀를 소개합니다. 이는 특정 참조 값을 가지고 있습니다. 이제 도움이 필요한 친구들이 참조할 수 있습니다.

앞서 언급했듯이 재귀는 큰 문제를 작은 문제로 나누는 솔루션입니다. 일반적으로 재귀를 함수 자체에 대한 호출이라고 합니다. 이렇게 말하는 것이 이상하게 들릴 수도 있지만 실제로 재귀에서 함수는 자신을 호출해야 합니다.

밤나무

예를 들어 수학에서 우리 모두는 "계승"이라는 개념을 알고 있습니다. 예를 들어 5의 계승은 `54321`입니다.

5*4*3*2*1。

5！= 5 * 4！
4！= 4 * 3！
3！= 3 * 2！
2！= 2 * 1！
1！= 1 * 0！
0！= 1

我们可以总结出求n的阶乘的规律，即 n! = n * (n -1) !

这就体现了递归。你可以从中发现，我们把求5的阶乘一步一步转化成了另外一个个的小问题。

递归算法的特性

每一个递归调用都必须基于一个小的子问题。例如5的阶乘就是5乘4的阶乘。
递归必须有一个Base case。例如阶乘的Base case就是0，当条件是0的时候，就停止递归。
递归中避免循环调用，否则最后计算机会显示栈溢出的错误。

function factorial(int $n): int
{
    if ($n = 0) {
        return 1;
    }
    
    return $n * factorial($n - 1);
}

看上面的代码，我们可以看到对于阶乘问题的解决方案我们有一个基础的条件就是当n为0的时候，我们返回1。如果不符合这个条件，我们返回n 乘 factorial(n)

5! = 5 * 4!

4! = 4 * 3!

3! = 3 * 2!

2! = 2 * 1!

PHP 데이터 구조를 기반으로 한 재귀

1! = 1 * 0!

0! = 1

PHP 데이터 구조를 기반으로 한 재귀

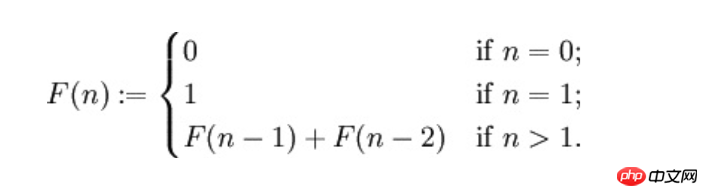
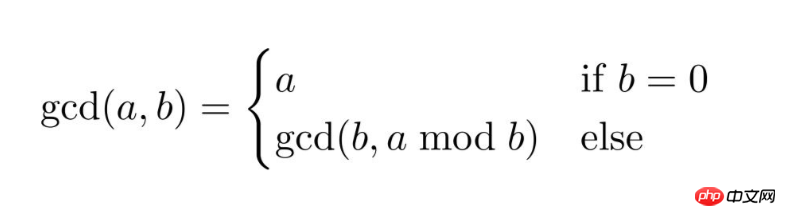
n의 계승을 찾는 규칙, 즉 n! = n * (n -1) !

재귀 알고리즘의 특성

모든 재귀 호출은 작은 하위 문제를 기반으로 해야 합니다. 예를 들어, 5의 계승은 5 곱하기 4의 계승입니다.

재귀에는 기본 사례가 있어야 합니다. 예를 들어 계승의 기본 사례는 0입니다. 조건이 0이면 재귀가 중지됩니다.

재귀 중에 루프 호출을 피하세요. 그렇지 않으면 컴퓨터에 결국 스택 오버플로 오류가 표시됩니다.

```
function factorial(int $n): int
{
    $result = 1;
    
    for ($i = $n; $i > 0; $i--) {
        $result*= $n;
    }
    
    return $result;
}
```
위의 코드를 보면 계승 문제를 풀기 위한 기본 조건이 있다는 것을 알 수 있습니다. 즉, n이 0일 때 1을 반환한다는 것입니다. 이 조건이 충족되지 않으면 첫 번째와 세 번째 재귀 속성을 준수하는 factorial(n)을 곱한 n을 반환합니다. 각 재귀 호출을 더 큰 문제의 더 작은 하위 문제로 나누기 때문에 반복 호출을 방지합니다. 위의 알고리즘 아이디어는 다음과 같이 표현할 수 있습니다.

반복 방법을 사용하여 위의 재귀 코드를 구현할 수도 있습니다

function fibonacci($n)
{
    if ($n == 0) {
        return 0;
    }
    
    if ($n == 1) {
        return 1;
    }
    
    return fibonacci($n - 1) + fibonacci($ - 2);
}

문제가 반복을 사용하여 쉽게 해결될 수 있다면 왜 재귀를 사용해야 할까요?

재귀는 더 복잡한 문제를 처리하는 데 사용됩니다. 단순히 반복을 사용하여 모든 문제를 해결할 수 있는 것은 아닙니다. 재귀는 함수 호출을 사용하여 호출 스택을 관리하므로 재귀는 반복보다 더 많은 시간과 메모리를 사용합니다. 또한 반복에서는 각 단계에서 결과를 얻지만 재귀에서는 결과를 얻기 전에 기본 사례 실행이 끝날 때까지 기다려야 합니다. 위의 예를 보면 재귀 알고리즘에서는 결과를 저장할 변수나 선언이 없는 반면, 반복 알고리즘에서는 $result를 사용하여 매번 반환된 결과를 저장합니다.

피보나치 수열

수학에서 피보나치 수열은 특별한 정수 수열입니다. 수열의 각 숫자는 다른 두 숫자의 합으로 생성됩니다. 규칙은 다음과 같습니다:

function gcd(int $a, int $b)
{
    if ($b == 0) {
        return $a;
    }
    
    return gcd($b, $a % $b);
}

재귀 알고리즘을 사용하는 또 다른 일반적인 문제는 두 숫자의 최대 공약수를 찾는 것입니다.

PHP 데이터 구조를 기반으로 한 재귀

rrreee

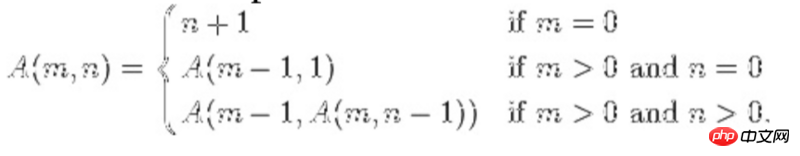
재귀 유형

선형 재귀

🎜🎜🎜각 재귀 호출에서 함수는 자신을 한 번만 호출하는데, 이를 선형 재귀라고 합니다. 🎜🎜🎜🎜Biary Recursion🎜🎜🎜🎜이진 재귀에서는 함수에 대한 각 재귀 호출이 자신을 두 번 호출합니다. 피보나치 수열을 푸는 알고리즘은 이진 재귀이며, 그 밖에 이진 검색, 분할 정복 알고리즘, 병합 정렬 등도 이진 재귀를 사용합니다. 🎜🎜🎜🎜꼬리 재귀🎜🎜🎜🎜재귀가 대기 작업 없이 반환되는 경우를 꼬리 재귀라고 합니다. 피보나치 알고리즘에서는 반환값에 이전 재귀의 반환값을 곱해야 하기 때문에 꼬리 재귀가 아니며, 최대공약수를 푸는 알고리즘은 꼬리 재귀이다. 꼬리 재귀는 선형 재귀의 한 형태입니다. 🎜🎜🎜🎜상호 재귀🎜🎜🎜🎜예를 들어 각 재귀 호출에서 A()는 B()를 호출하고 B()는 A()를 호출합니다. 🎜🎜🎜🎜중첩 재귀🎜🎜🎜🎜재귀 함수가 자신을 매개변수로 재귀적으로 호출하는 것을 중첩 재귀라고 합니다. 일반적인 예는 Ackerman 함수입니다. 아래 표현식을 참조하세요. 🎜🎜🎜🎜🎜마지막 줄을 보시면 두 번째 매개변수가 재귀함수 그 자체임을 알 수 있습니다. 🎜🎜다음 섹션🎜🎜다음 기사에서는 재귀를 사용하여 N 수준 분류 구축, 중첩 주석 구축, 디렉터리 파일 탐색 등과 같은 실제 개발에서 직면하는 몇 가지 문제를 해결합니다. 🎜

위 내용은 이 글의 전체 내용입니다. 모든 분들의 학습에 도움이 되길 바랍니다. 더 많은 관련 내용은 PHP 중국어 홈페이지를 참고해주세요!

PHP 데이터 구조를 기반으로 한 재귀

예를 들어 수학에서 우리 모두는 "계승"이라는 개념을 알고 있습니다. 예를 들어 5의 계승은 5*4*3*2*1입니다.

递归算法的特性

n의 계승을 찾는 규칙, 즉 n! = n * (n -1) !

관련 기사

예를 들어 수학에서 우리 모두는 "계승"이라는 개념을 알고 있습니다. 예를 들어 5의 계승은 `54321`입니다.