TensorFlow를 사용한 Deming 회귀 알고리즘 구현 예
- 不言원래의
- 2018-05-02 13:55:082553검색
이 글에서는 주로 TensorFlow를 사용하여 Deming 회귀 알고리즘을 구현한 예를 소개합니다. 이제 특정 참조 값이 있으므로 필요한 친구들이 참조할 수 있습니다.
최소 제곱 선형 회귀 알고리즘을 최소화하면 수직 거리의 회귀 직선(즉, y축 방향에 평행)이면 데밍 회귀는 회귀선(즉, 회귀선에 수직)까지의 전체 거리를 최소화합니다. x 값과 y 값의 양방향 오차를 최소화합니다. 구체적인 비교 차트는 다음과 같습니다.
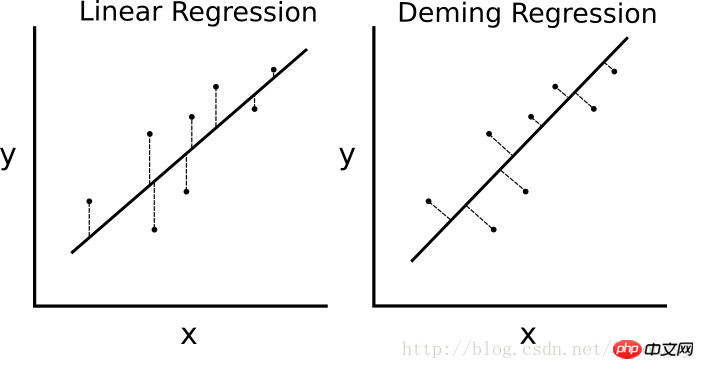
선형 회귀 알고리즘과 데밍 회귀 알고리즘의 차이점. 왼쪽의 선형 회귀는 회귀선까지의 수직 거리를 최소화하고, 오른쪽의 데밍 회귀는 회귀선까지의 전체 거리를 최소화합니다.
선형 회귀 알고리즘의 손실 함수는 수직 거리를 최소화합니다. 여기서는 전체 거리를 최소화해야 합니다. 직선의 기울기와 절편이 주어지면 점에서 직선까지의 수직 거리를 풀 수 있는 알려진 기하학적 공식이 있습니다. 기하학적 공식을 대입하고 TensorFlow가 거리를 최소화하도록 하세요.
손실 함수는 분자와 분모로 구성된 기하학적 공식입니다. 직선 y=mx+b와 점(x0, y0)이 주어지면 둘 사이의 거리를 구하는 공식은 다음과 같습니다.
이 글 데밍 회귀 알고리즘과 선형 회귀 알고리즘으로 얻은 결과는 기본적으로 동일합니다. 둘 사이의 주요 차이점은 예측 값과 데이터 포인트 사이의 손실 함수 측정입니다. 선형 회귀 알고리즘의 손실 함수는 수직 거리 손실인 반면 데밍 회귀 알고리즘은 수직 거리 손실입니다. x축 및 y축 거리 손실).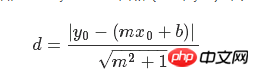 여기서 데밍 회귀 알고리즘의 구현 유형은 전체 회귀(총 최소 제곱 오류)입니다. 전체 회귀 알고리즘은 x와 y 값의 오류가 유사하다고 가정합니다. 또한 다양한 오류를 사용하여 다양한 개념에 따라 x축과 y축의 거리 계산을 확장할 수 있습니다.
여기서 데밍 회귀 알고리즘의 구현 유형은 전체 회귀(총 최소 제곱 오류)입니다. 전체 회귀 알고리즘은 x와 y 값의 오류가 유사하다고 가정합니다. 또한 다양한 오류를 사용하여 다양한 개념에 따라 x축과 y축의 거리 계산을 확장할 수 있습니다.
관련 권장 사항:
TensorFlow를 사용하여 다중 클래스 서포트 벡터 머신을 구현하기 위한 샘플 코드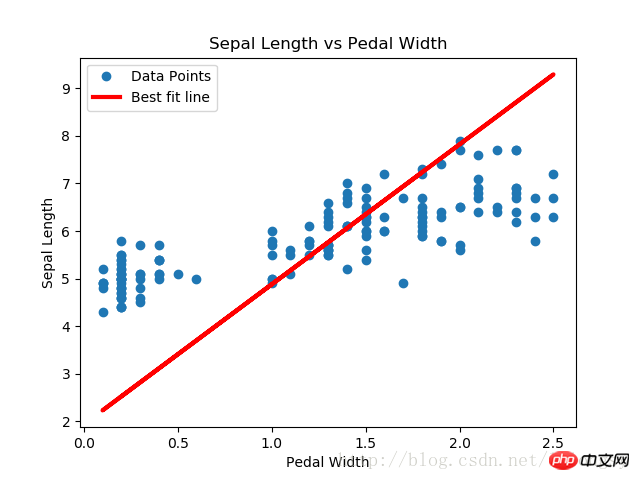 비선형 서포트 벡터 머신을 위한 TensorFlow 구현 방법
비선형 서포트 벡터 머신을 위한 TensorFlow 구현 방법
위 내용은 TensorFlow를 사용한 Deming 회귀 알고리즘 구현 예의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!

