깊이 우선 및 너비 우선 알고리즘 예제에 대한 자세한 설명

먼저 Algorithms 책의 온라인 강좌인 알고리즘 웹사이트의 두 번째 부분을 소개하겠습니다.

그리고 Coursera의 그래프 알고리즘 강좌도 매우 좋습니다.

그래프를 표현하는 여러 가지 방법:

이러한 방식(데이터 구조)을 사용하여 그래프를 표현하려면 다음 두 가지 요구 사항이 포함됩니다. (1) 공간이 적절해야 합니다. (2) 인스턴스 메소드 구현은 빨라야 합니다

그런 다음 세 가지 옵션이 있습니다:

(1) 다음과 같은 가장자리 세트:

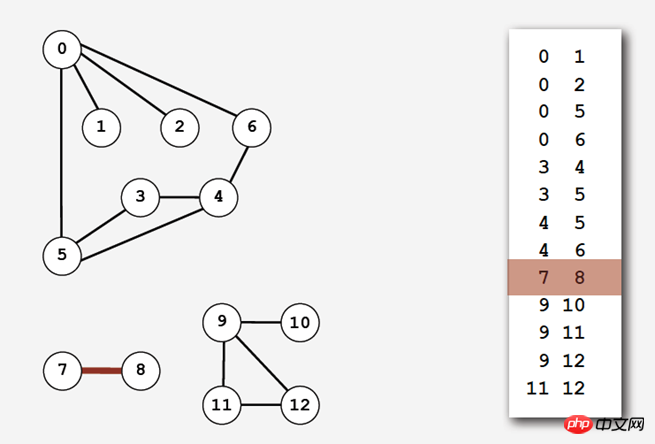
간단하지만 두 번째를 충족하지 않습니다. 조건 - 인접성을 달성하기 위해 테이블 ​​adj()는 그래프의 모든 가장자리를 탐색합니다.

(2) 인접 행렬:

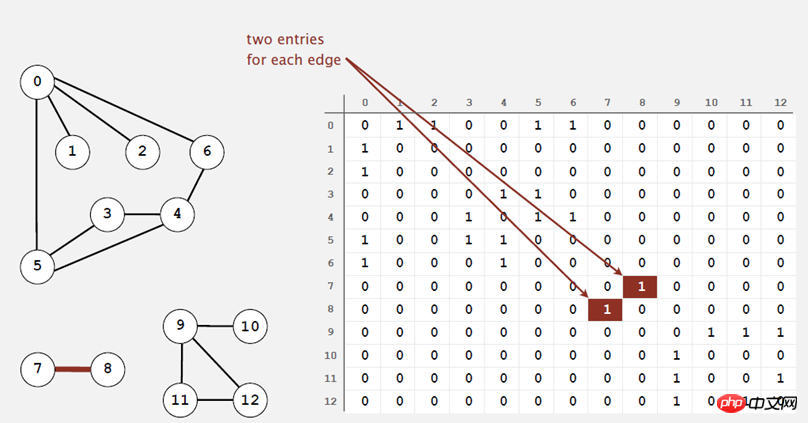
V 곱하기 V 부울 증명을 사용하면 공간에서 만족되지 않습니다.

(3) 인접 목록:

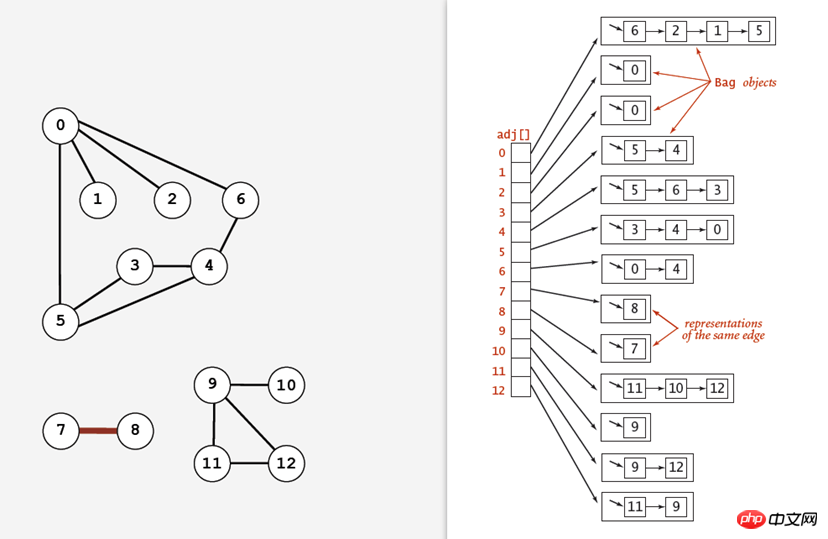
은 정점을 인덱스로 사용하는 배열 목록을 사용하며, 그 안의 각 요소는 정점에 인접한 정점의 목록입니다.

위 방법의 유연성이 더 높으므로 인접 리스트로 표현하는 경우 다음과 같은 데이터 구조를 정의하여 Graph 객체를 표현할 수 있습니다.

public class Graph
{private readonly int verticals;//顶点个数private int edges;//边的个数private List<int>[] adjacency;//顶点联接列表public Graph(int vertical)
    {this.verticals = vertical;this.edges = 0;
        adjacency=new List<int>[vertical];for (int v = 0; v < vertical; v++)
        {
            adjacency[v]=new List<int>();
        }
    }public int GetVerticals ()
    {return verticals;
    }public int GetEdges()
    {return edges;
    }public void AddEdge(int verticalStart, int verticalEnd)
    {
        adjacency[verticalStart].Add(verticalEnd);
        adjacency[verticalEnd].Add(verticalStart);
        edges++;
    }public List<int> GetAdjacency(int vetical)
    {return adjacency[vetical];
    }
}

깊이 우선 알고리즘

깊이 우선 알고리즘에 대해 이야기하기 전에 먼저 미로 탐색 문제를 살펴볼 수 있습니다. 다음은 미로와 그래프의 대응 관계입니다.

미로의 각 교차점은 그래프의 꼭지점을 나타내고 각 채널은 모서리에 해당합니다.

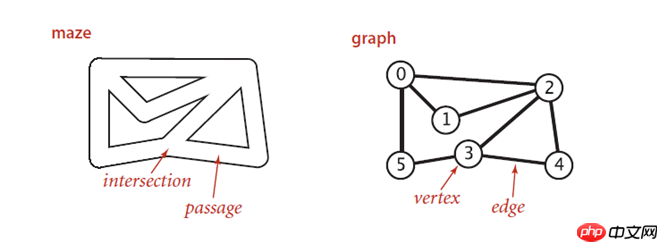
트레모 로프 탐사 방법을 사용하여 미로를 탐색할 수 있습니다. 즉,

• 뒤에 밧줄을 두세요

• 방문하는 모든 장소에 밧줄을 놓아 방문하는 교차점과 통로를 표시하세요

• 이미 가본 장소를 만날 때 방문하고 이전에 방문하지 않은 장소로 로프를 따라 돌아갑니다.

그림은 다음과 같습니다.

다음은 미로 탐험의 작은 애니메이션입니다.

깊이 우선 검색 알고리즘은 미로 탐색을 시뮬레이션합니다. 실제 그래프 처리 알고리즘에서는 일반적으로 그래프 표현과 그래프 처리 논리를 분리합니다. 따라서 알고리즘의 전반적인 디자인 패턴은 다음과 같습니다.

• 그래프 개체 만들기

• Graph 개체를 Paths 개체와 같은 그래프 알고리즘 처리 개체에 전달

• 그런 다음 처리된 결과를 쿼리하여 정보를 얻으려면

dfs 메서드가 재귀적으로 호출되고 표시된[] 표시 배열을 유지하며 호출하기 전에 노드를 방문했는지 여부를 확인합니다.

깊이 우선 알고리즘 설명: 정점을 방문할 때

1. 방문했다고 표시합니다.

2.

public class DepthFirstSearch
{private bool[] marked;//记录顶点是否被标记private int count;//记录查找次数private DepthFirstSearch(Graph g, int v)
    {
        marked = new bool[g.GetVerticals()];
        dfs(g, v);
    }private void dfs(Graph g, int v)
    {
        marked[v] = true;
        count++;foreach (int vertical in g.GetAdjacency(v))
        {if (!marked[vertical])
                dfs(g,vertical);
        }
    }public bool IsMarked(int vertical)
    {return marked[vertical];
    }public int Count()
    {return count;
    }
}

试验一个算法最简单的办法是找一个简单的例子来实现。

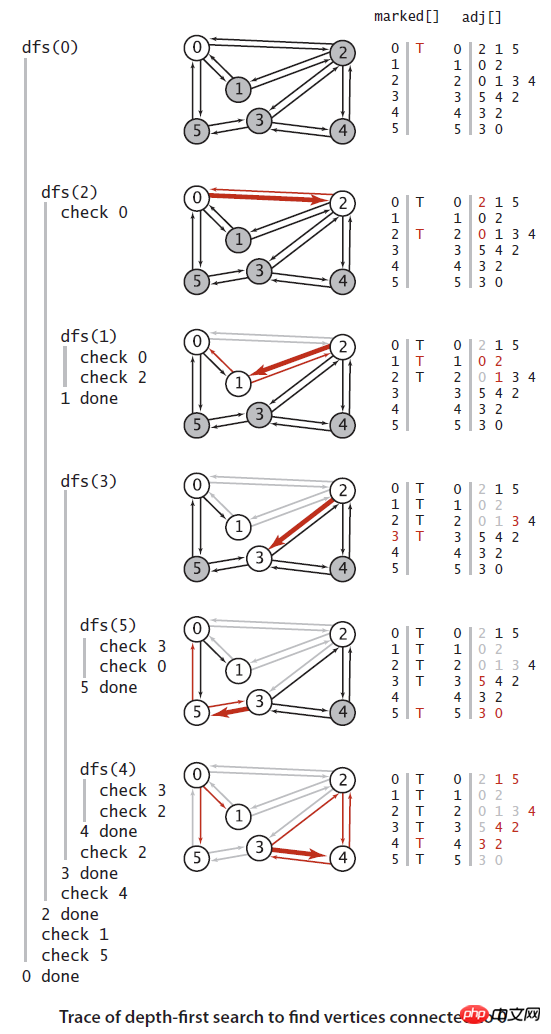
算法应用：

连通性。给定一幅图，回答“两个给定顶点是否连通？” 或者 “图中有多少个连通子图？”

寻找路径。给定一幅图和一个起点，回答“从s到给定目的顶点v是否存在一条路径？如果有，找出这条路径。”

检测环。给定的图是无环图吗？

双色问题。能够用两种颜色将图的所有顶点着色，使得任意一条边连个顶点的颜色都不相同？这个问题等价于：这是一个二分图吗？

 

深度优先路径查询

有了这个基础，我们可以实现基于深度优先的路径查询，要实现路径查询，我们必须定义一个变量来记录所探索到的路径。

所以在上面的基础上定义一个edgesTo变量来后向记录所有到s的顶点的记录，和仅记录从当前节点到起始节点不同，我们记录图中的每一个节点到开始节点的路径。为了完成这一日任务，通过设置edgesTo[w]=v，我们记录从v到w的边，换句话说，v-w是做后一条从s到达w的边。 edgesTo[]其实是一个指向其父节点的树。

注意代码只是在前面算法的基础上维护了一个edgTo数组，并用栈Stack保存路径。

public class DepthFirstPaths
{private bool[] marked;//记录是否被dfs访问过
    private int[] edgesTo;//记录最后一个到当前节点的顶点private int s;//搜索的起始点public DepthFirstPaths(Graph g, int s)
    {
        marked = new bool[g.GetVerticals()];
        edgesTo = new int[g.GetVerticals()];this.s = s;
        dfs(g, s);
    }private void dfs(Graph g, int v)
    {
        marked[v] = true;foreach (int w in g.GetAdjacency(v))
        {if (!marked[w])
            {                edgesTo[w] = v;dfs(g,w);
            }
        }
    }public bool HasPathTo(int v)
    {return marked[v];
    }public Stack<int> PathTo(int v){if (!HasPathTo(v)) return null;
        Stack<int> path = new Stack<int>();for (int x = v; x!=s; x=edgesTo[x])
        {
            path.Push(x);
        }
        path.Push(s);return path;
    }
}

 

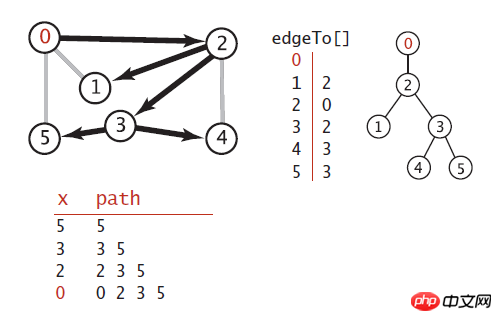
上图中是黑色线条表示 深度优先搜索中，所有定点到原点0的路径， 他是通过edgeTo[]这个变量记录的，可以从右边可以看出，

他其实是一颗树，树根即是原点，每个子节点到树根的路径即是从原点到该子节点的路径。

下图是深度优先搜索算法的一个简单例子的追踪。

 

 

 

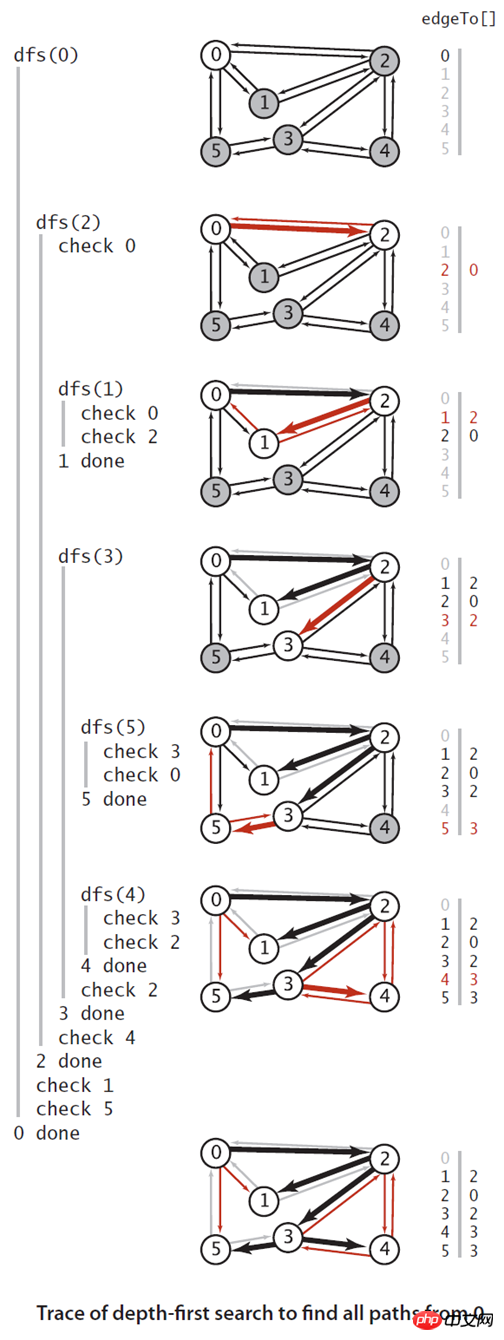
连通分量

API如下：

CC的实现使用了marked[ ]数组来寻找一个顶点作为每个连通分量中深度优先搜索的起点。递归的深搜第一次调用的参数是顶点0，会标记所有与0连通的顶点。然后构造函数中的for循环会查找每个没有被标记的顶点并递归调用dfs来标记和它相邻的所有顶点。另外，它还使用了一个以顶点作为索引的数组id[ ],将同一个连通分量中的顶点和连通分量的标识符关联起来。这个数组使得connected( )方法的实现变得十分简单。

public class CC {private boolean[] marked;private int[] id;private int count;public CC(Graph g){
        marked = new boolean[g.getVertexCount()];
        id = new int[g.getVertexCount()];for(int s = 0; s < g.getVertexCount(); s++){if(!marked[s]){
                dfs(g,s);
                count++;
            }
        }
    }private void dfs(Graph g, int v) {
        marked[v] = true;
        id[v] = count;for(int w: g.adj(v))if(!marked[w])
                dfs(g,w);
    }/** v和w连通吗*/public boolean connected(int v, int w)    { return id[v] == id[w]; }/** v所在的连通分量的标识符*/public int id(int v)    { return id[v]; }/** 连通分量数*/public int count()        {return count;}

 

检测环

/**
 * 给定的图是无环图吗
 * 检测自环:假设没有自环，没有平行边 */public class Cycle {private boolean[] marked;private boolean hasCycle;public Cycle(Graph g){
        marked = new boolean[g.getVertexCount()];for(int i = 0;i<g.getVertexCount();i++)if(!marked[i])    dfs(g, i, i);
    }private void dfs(Graph g, int v, int u) {
        marked[v] = true;for(int w: g.adj(v))if(!marked[w])    dfs(g, w, v); // 若w没被标记过，那么从w继续递归深搜，把w的父节点作为第二参数else if(w != u) hasCycle = true; // 若w被标记过，那么若无环，w必然和父节点相同，否则就是有环    }/** 是否含有环*/public boolean hasCycle(){return hasCycle;}

 

双色问题

/**
 * 双色问题：能够用两种颜色将图的所有顶点着色，使得任意一条边上的两个端点的颜色都不同吗？
 * 等价于：判断是否是二分图的问题 */public class TwoColor {private boolean[] marked;private boolean[] color;private boolean isColorable;public TwoColor(Graph g){
        isColorable = true;
        marked = new boolean[g.getVertexCount()];
        color = new boolean[g.getVertexCount()];for(int i = 0; i<g.getVertexCount(); i++)//遍历所有顶点if(!marked[i])    dfs(g, i);//没有mark就进行深搜    }private void dfs(Graph g, int v) {
        marked[v] = true;        // 标记for(int w: g.adj(v))    // 对邻接表进行遍历if(!marked[w]){        // 如果没有被标记color[w] = !color[v];    // 当前w节点颜色置为和父节点不同的颜色dfs(g, w);                // 对当前节点继续深搜}else if(color[w] == color[v]){    // 如果已经被标记，看是否颜色和父节点相同isColorable = false;         // 若相同则不是二分图            }
    }/** 是否是二分图*/public boolean isBipartite(){return isColorable;}

 

 

广度优先算法

通常我们更关注的是一类单源最短路径的问题，那就是给定一个图和一个源S，是否存在一条从s到给定定点v的路径，如果存在，找出最短的那条(这里最短定义为边的条数最小)

深度优先算法是将未被访问的节点放到一个堆中(stack)，虽然在上面的代码中没有明确在代码中写stack，但是 递归间接的利用递归堆实现了这一原理。

和深度优先算法不同， 广度优先是将所有未被访问的节点放到了队列中。其主要原理是：

先将起点加入队列，然后重复一下步骤直到队列为空：

1.取队列中的下一个顶点V并标记它

2.将与v相邻的所有未被标记过的顶点加入队列

广度优先是以距离递增的方式来搜索路径的。

class BreadthFirstSearch
{private bool[] marked;private int[] edgeTo;private int sourceVetical;//Source verticalpublic BreadthFirstSearch(Graph g, int s)
    {
        marked=new bool[g.GetVerticals()];
        edgeTo=new int[g.GetVerticals()];this.sourceVetical = s;
        bfs(g, s);
    }private void bfs(Graph g, int s)
    {
        Queue<int> queue = new Queue<int>();
        marked[s] = true;
        queue.Enqueue(s);while (queue.Count()!=0)
        {int v = queue.Dequeue();foreach (int w in g.GetAdjacency(v))
            {if (!marked[w])
                {
                    edgeTo[w] = v;
                    marked[w] = true;
                    queue.Enqueue(w);
                }
            }
        }
    }public bool HasPathTo(int v)
    {return marked[v];
    }public Stack<int> PathTo(int v)
    {if (!HasPathTo(v)) return null;

        Stack<int> path = new Stack<int>();for (int x = v; x!=sourceVetical; x=edgeTo[x])
        {
            path.Push(x);
        }
        path.Push(sourceVetical);return path;
    }

}

算法应用：最短路径问题

 

总结：

深度优先搜索和广度优先搜索都是将起点存入数据结构中，然后重复一下步骤直到数据结构被清空：

1.取其中的下一个顶点并标记它

2.将v的所有相邻而未被标记的顶点加入数据结构

这两个算法 的不同之处仅在于从数据结构中获取下一个顶点的规则（广度优先来说是最早加入的顶点，对于深度优先搜索来说是最晚加入的顶点）。

 

위 내용은 깊이 우선 및 너비 우선 알고리즘 예제에 대한 자세한 설명의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!