JS를 사용하여 이진 검색 트리 설정 및 일부 순회 방법 구현

이 글에서는 주로 JS에서 구현된 이진 검색 트리의 구축과 일부 순회 방법의 구현을 소개합니다. 이는 특정 참조 값을 가지며 관심 있는 친구들이 참조할 수 있습니다.

이진 검색 트리는 노드(Node)와 에지(Edge)로 구성됩니다.

노드 데이터와 왼쪽 및 오른쪽 하위 노드를 저장하는 노드 클래스 Node를 정의한 다음 데이터를 표시하는 방법을 정의할 수 있습니다.

//以下定义一个节点类
function Node(data,left,right){
  // 节点的键值
  this.data = data;
  // 左节点
  this.left = left;
  // 右节点
  this.right = left;
  // 显示该节点的键值
  this.show = show;
}
// 实现show方法
function show(){
  return this.data;
}

는 트리의 루트 노드를 정의하고 이를 null로 초기화한 후 노드를 삽입하는 방법과 한쪽을 횡단하는 방법을 정의하는 이진 검색 트리 클래스 BST를 정의합니다.

// 二叉查找树BST
// 有一个节点属性，还有一些其他的方法，以下定义一个二叉查找树BST类
function BST(){
  // 根节点初始化为空
  this.root = null;
  // 方法
  // 插入
  this.insert = insert;
  // JS를 사용하여 이진 검색 트리 설정 및 일부 순회 방법 구현
  this.inorder = inorder;
  // JS를 사용하여 이진 검색 트리 설정 및 일부 순회 방법 구현
  this.preorder = preorder;
  // JS를 사용하여 이진 검색 트리 설정 및 일부 순회 방법 구현
  this.postorder = postorder;
}

//实现insert插入方法
function insert(data){
  // 创建一个节点保存数据
  var node = new Node(data,null,null);
  // 下面将节点node插入到树中
  // 如果树是空的，就将节点设为根节点
  if(!this.root){
    this.root = node;
  }else{ //树不为空
    // 判断插在父节点的左边还是右边
    // 所以先要保存一下父节点
    // var parent = this.root;
    var current = this.root;
    var parent;
    // 如果要插入的节点键值小于父节点键值，则插在父节点左边，
    // 前提是父节点的左边为空，否则要将父节点往下移一层，
    // 然后再做判断
    while(true){
      // data小于父节点的键值
      parent = current;
      if(data < parent.data){
        // 将父节点往左下移(插入左边)
        // parent = parent.left;
        current = current.left;
        // 如果节点为空，则直接插入
        if(!current){
          // ！！！此处特别注意，如果就这样把parent赋值为node，也仅仅只是parent指向node，
          // 而并没有加到父元素的左边！！！根本没有加到树中去。所以要先记住父元素，再把当前元素加入进去
          parent.left = node;
          break;
        }      
      }else{ // 将父节点往右下移(插入右边)
        current = current.right;
        if(!current){
          parent.right = node;
          break;
        }
      }
    }

  }
} 

//实现inorder遍历方法(左中右)
function inorder(node){
  if(node){
    inorder(node.left);
    console.log(node.show());
    inorder(node.right);
  }
}

// JS를 사용하여 이진 검색 트리 설정 및 일부 순회 방법 구현(中左右)
function preorder(node){
  if(node){
    console.log(node.show());
    preorder(node.left);
    preorder(node.right);
  }
}

// JS를 사용하여 이진 검색 트리 설정 및 일부 순회 방법 구현(左右中)
function postorder(node){
  if(node){
    preorder(node.left);
    preorder(node.right);
    console.log(node.show());
  }
}

테스트:

// JS를 사용하여 이진 검색 트리 설정 및 일부 순회 방법 구현(左右中)
function postorder(node){
  if(node){
    postorder(node.left);
    postorder(node.right);
    console.log(node.show());
  }
}

// 实例化一个BST树
var tree = new BST();
// 添加节点
tree.insert(30);
tree.insert(14);
tree.insert(35);
tree.insert(12);
tree.insert(17);
// JS를 사용하여 이진 검색 트리 설정 및 일부 순회 방법 구현
tree.inorder(tree.root);
// JS를 사용하여 이진 검색 트리 설정 및 일부 순회 방법 구현
tree.preorder(tree.root);
// JS를 사용하여 이진 검색 트리 설정 및 일부 순회 방법 구현
tree.postorder(tree.root);

결과:

순서 순회:

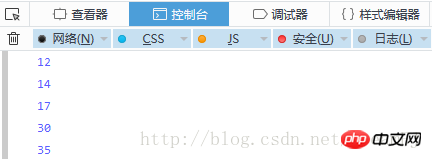
선주문 순회:

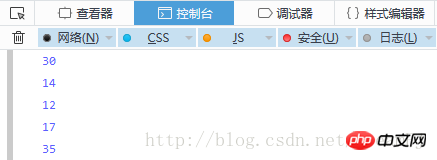
후순 순회:

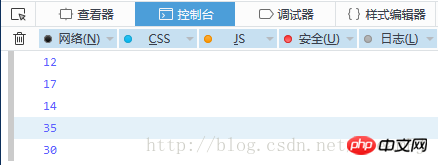
위 내용은 JS를 사용하여 이진 검색 트리 설정 및 일부 순회 방법 구현의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!