그래프 간선 가중치 수정
- WBOY원래의
- 2024-08-31 06:35:321292검색
2699. 그래프 가장자리 가중치 수정
난이도:어려움
주제: 그래프, 힙(우선순위 대기열), 최단 경로
0부터 n - 1까지 레이블이 지정된 n개의 노드를 포함하는 무방향 가중치 연결 그래프와 가장자리[i] = [ai, b인 정수 배열 가장자리가 제공됩니다. i, wi]는 가중치가 wii와 bi 사이에 간선이 있음을 나타냅니다. 🎜>.
일부 모서리의 가중치는 -1(wi = -1)인 반면 다른 모서리의 가중치는 양수(wi > 0)입니다. .
당신의 임무는 [1, 2 * 109 범위에서 양의 정수 값을 할당하여 가중치 -1로 모든 모서리를 수정하는 것입니다. ] 노드 소스와 대상 사이의 최단 거리가 정수 타겟과 같아지도록 합니다. 소스와 대상 사이의 최단 거리를 대상과 동일하게 만드는 여러 수정이 있는 경우 모두 올바른 것으로 간주됩니다. 소스에서 대상까지의 최단 거리를 대상과 동일하게 만드는 것이 가능한 경우
모든 가장자리(수정되지 않은 가장자리도 포함)를 순서에 관계없이 포함하는 배열을 반환하고, 불가능한 경우빈 배열을 반환합니다. .
참고:초기 양수 가중치가 있는 간선의 가중치를 수정할 수 없습니다.
예 1:
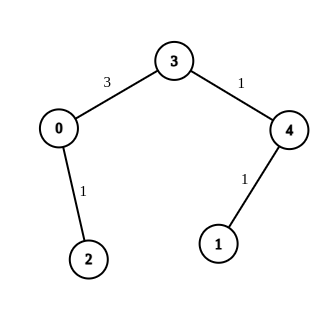
- 입력:
- n = 5, 가장자리 = [[4,1,-1],[2,0,-1],[0,3,-1],[4,3,-1] ], 소스 = 0, 대상 = 1, 대상 = 5 출력:
- [[4,1,1],[2,0,1],[0,3,3],[4,3,1]] 설명:
- 위 그래프는 0에서 1까지의 거리를 5와 동일하게 만드는 가장자리 수정 가능성을 보여줍니다.
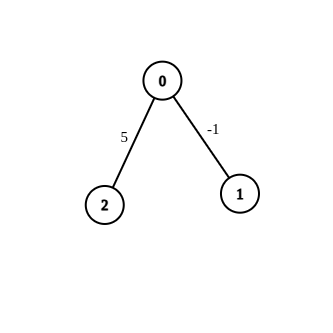
- 입력:
- n = 3, 가장자리 = [[0,1,-1],[0,2,5]], 소스 = 0, 대상 = 2, 대상 = 6 출력:
- [] 설명:
- 위 그래프에는 초기 간선이 포함되어 있습니다. 가중치 -1로 가장자리를 수정하여 0에서 2까지의 거리를 6과 동일하게 만드는 것은 불가능합니다. 따라서 빈 배열이 반환됩니다.
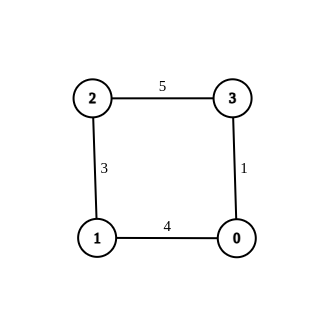
- 입력:
- n = 4, 가장자리 = [[1,0,4],[1,2,3],[2,3,5],[0,3,-1]], 소스 = 0, 목적지 = 2, 대상 = 6 출력:
- [[1,0,4],[1,2,3],[2,3,5],[0,3,1]] 설명:
- 위 그래프는 0에서 2까지의 최단 거리를 6으로 변형한 그래프입니다.
1
먼저 소스에서 대상까지의 최단 경로를 타겟과 동일하게 만드는 것이 실제로 가능한지 확인하세요.
- 수정할 모서리가 없는 원본에서 대상까지의 최단 경로가 대상보다 작으면 불가능합니다.
- 수정할 가장자리를 포함하고 임시 가중치 1을 할당하는 소스에서 대상까지의 최단 경로가 목표보다 큰 경우에도 불가능합니다.
- 소스에서 u까지의 최단 경로 길이(dis1)와 v에서 대상까지의 최단 경로 길이(dis2)가 타겟(dis1)보다 작도록 수정 가능한 에지(u, v)를 찾을 수 있다고 가정합니다. + dis2 < target), 가중치를 "target - dis1 - dis2"로 변경할 수 있습니다.
- 아직 가중치가 "-1"인 다른 모든 가장자리의 경우 가중치를 충분히 큰 수(목표, 목표 + 1 또는 200000000 등)로 변경합니다.
접근 방식을 다음과 같이 분류할 수 있습니다.
접근하다:
- 기존 가중치를 사용한 초기 점검:
- 먼저, 가중치가 -1인 가장자리는 무시하고 양의 가중치를 갖는 가장자리만 사용하여 소스에서 대상까지의 최단 경로를 계산합니다.
- 이 거리가 이미 목표보다 크다면 목표를 달성하기 위해 -1 가장자리를 수정할 수 없으므로 빈 배열을 반환합니다.
-
임시 가중치 부여 1:
- 다음으로 가중치가 -1인 모든 가장자리에 임시 가중치 1을 할당하고 최단 경로를 다시 계산합니다.
- 이 최단 경로가 여전히 목표보다 크면 목표를 달성하는 것이 불가능하므로 빈 배열을 반환합니다.
-
특정 가장자리 가중치 수정:
- 가중치 -1로 가장자리를 반복하고 목표 거리와 정확히 일치하도록 조정될 수 있는 가장자리를 식별합니다. 이는 이 가장자리로 향하는 경로와 가장자리에서 나오는 경로의 결합된 거리가 정확한 목표 거리가 되도록 가장자리의 가중치를 조정하여 수행됩니다.
- 나머지 -1 에지에는 최단 경로에 영향을 주지 않도록 충분히 큰 가중치(예: 2 * 10^9)를 할당하세요.
-
수정된 가장자리 반환:
- 마지막으로 수정된 가장자리 목록을 반환합니다.
PHP에서 이 솔루션을 구현해 보겠습니다: 2699. 그래프 가장자리 가중치 수정
설명:
- dijkstra 함수는 소스에서 다른 모든 노드까지의 최단 경로를 계산합니다.
- 처음에는 -1 모서리를 무시하고 최단 경로를 계산합니다.
- -1 모서리가 없는 경로가 목표보다 작으면 함수는 빈 배열을 반환하여 목표를 충족하도록 가중치를 조정할 수 없음을 나타냅니다.
- 그렇지 않으면 일시적으로 모든 -1 가장자리를 1로 설정하고 최단 경로가 목표를 초과하는지 확인합니다.
- 그렇다면 다시 목표에 도달하는 것이 불가능하며 빈 배열을 반환합니다.
- 그런 다음 -1 모서리의 가중치를 전략적으로 수정하여 정확한 목표의 원하는 최단 경로를 달성합니다.
이 접근 방식은 가장자리 가중치를 효율적으로 확인하고 조정하여 가능한 경우 목표 거리가 충족되도록 합니다.
연락처 링크
이 시리즈가 도움이 되었다면 GitHub에서 저장소에 별표를 표시하거나 즐겨찾는 소셜 네트워크에서 게시물을 공유해 보세요. 여러분의 지원은 저에게 큰 의미가 될 것입니다!
이렇게 더 유용한 콘텐츠를 원하시면 저를 팔로우해주세요.
- 링크드인
- 깃허브
위 내용은 그래프 간선 가중치 수정의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!