javascript_javascript 스킬에서 4개의 연산식을 파싱하는 알고리즘 및 예

코드를 작성할 때 우리는 4개의 산술식을 직접 파싱해야 하는 상황에 직면할 때가 있습니다. 이 글에서는 간단한 4개의 산술식을 파싱하기 위해 JavaScript를 사용하는 방법을 간략하게 소개합니다.

1.익숙한 개념

중위 표기법 (또는 중위 표기법)은 산술 또는 논리식을 표현하는 일반적인 방법으로, 연산자는 중위 형식으로 피연산자 중간에 위치합니다(예: 3 4). 즉, 우리가 가장 일반적으로 사용하는 산술식인 중위식은 사람이 이해하기 쉽지만 컴퓨터가 구문 분석하기는 쉽지 않습니다.

역 폴란드 표기법(역 폴란드 표기법, RPN 또는 역 폴란드 표기법)은 폴란드 수학자 Jan Vukasiewicz가 1920년에 도입한 수학적 표현 방법입니다. 역 폴란드 표기법에서는 모든 연산자가 피연산자 뒤에 배치됩니다. , 그래서 접미사 표기법이라고도 합니다. 역폴란드 표기법에서는 연산자 우선 순위를 나타내기 위해 괄호가 필요하지 않습니다. 역 폴란드 표기법을 사용하면 스택 구조를 사용하여 표현식을 구문 분석하고 계산하기가 쉽습니다. 따라서 여기서는 먼저 중위 표현식을 역 폴란드 표현식으로 변환하여 4개의 요소 표현식을 구문 분석합니다. 그런 다음 값을 계산하십시오.

2. 변환 과정

중위 표현식을 후위 표현식으로 변환(스케줄링 필드 알고리즘)

1. 입력 대기열에 표시가 나타납니다
2. 토큰이 숫자인 경우 출력 대기열에 추가합니다
3. 연산자(-*/)인 경우 출력 스택 상단에 있는 연산자와 비교합니다. 우선 순위가 스택 상단에 있는 연산자보다 작거나 같으면 해당 연산자를 맨 위에 놓습니다. 스택을 복사하여 출력 대기열에 추가하고(위 조건이 충족되지 않을 때까지 반복) 마지막으로 이 연산자를 스택에 푸시합니다.
4. 왼쪽 괄호이면 스택에 밀어 넣습니다
5. 오른쪽 괄호인 경우 스택 맨 위에 있는 요소가 왼쪽 괄호가 될 때까지 스택에서 연산자를 계속해서 팝하고 출력 대기열에 추가합니다. 왼쪽 대괄호를 팝하고 출력 대기열에 추가하지 마십시오. 왼쪽 괄호가 발견되지 않으면 원래 표현식의 괄호가 대칭이 아니며 오류가 있음을 의미합니다.
6. 입력 큐가 비어 있고 스택에 여전히 연산자가 있는 경우, 스택 상단의 연산자가 왼쪽 괄호인 경우 원래 표현식에 일치하지 않는 괄호가 있음을 의미합니다. 스택에서 연산자를 하나씩 팝하여 출력 대기열에 추가합니다.
7. 완료

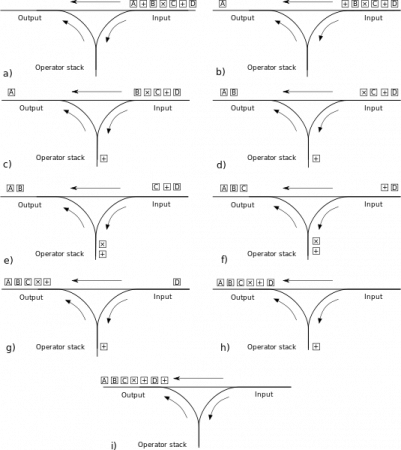
3. 코드 변환 구현

function isOperator(value){
	var operatorString = "+-*/()";
	return operatorString.indexOf(value) > -1
}

function getPrioraty(value){
	switch(value){
		case '+':
		case '-':
			return 1;
		case '*':
		case '/':
			return 2;
		default:
			return 0;
	}
}

function prioraty(o1, o2){
	return getPrioraty(o1) <= getPrioraty(o2);
}

function dal2Rpn(exp){
	var inputStack = [];
	var outputStack = [];
	var outputQueue = [];

	for(var i = 0, len = exp.length; i < len; i++){
		var cur = exp[i];
		if(cur != ' ' ){
			inputStack.push(cur);
		}
	}
	console.log('step one');
	while(inputStack.length > 0){
		var cur = inputStack.shift();
		if(isOperator(cur)){
			if(cur == '('){
				outputStack.push(cur);
			}else if(cur == ')'){
				var po = outputStack.pop();
				while(po != '(' && outputStack.length > 0){
					outputQueue.push(po);
					po = outputStack.pop();
				}
				if(po != '('){
					throw "error: unmatched ()";
				}
			}else{
				while(prioraty(cur, outputStack[outputStack.length - 1]) && outputStack.length > 0){
					outputQueue.push(outputStack.pop());
				}
				outputStack.push(cur);
			}
		}else{
			outputQueue.push(new Number(cur));
		}
	}
	console.log('step two');
	if(outputStack.length > 0){
		if(outputStack[outputStack.length - 1] == ')' || outputStack[outputStack.length - 1] == '('){
			throw "error: unmatched ()";
		}
		while(outputStack.length > 0){
			outputQueue.push(outputStack.pop());
		}
	}
	console.log('step three');
	return outputQueue;

}

console.log(dal2Rpn('1 + 2'));
console.log(dal2Rpn('1 + 2 + 3'));
console.log(dal2Rpn('1 + 2 * 3'));
console.log(dal2Rpn('1 + 2 * 3 - 4 / 5'));
console.log(dal2Rpn('( 1 + 2 )'));

console.log(dal2Rpn('( 1 + 2 ) * ( 3 - 4 ) / 5'));
console.log(dal2Rpn('( 1 + 2 ) * (( 3 - 4 ) / 5)'));

4. 역폴란드 표현 평가

1. 입력 대기열에서 토큰을 팝합니다
2. 피연산자라면 출력 스택에 추가하세요
3. 연산자인 경우 출력 스택에서 두 피연산자를 팝하여 계산을 수행하고 계산된 값을 출력 스택에 푸시합니다.
4. 루프 작업, 입력 큐가 비어 있고 출력 스택에 숫자가 하나만 있으면 이 숫자가 결과이고, 그렇지 않으면 중복 피연산자가 있습니다.

5. 계산 코드

function evalRpn(rpnQueue){
	var outputStack = [];
	while(rpnQueue.length > 0){
		var cur = rpnQueue.shift();

		if(!isOperator(cur)){
			outputStack.push(cur);
		}else{
			if(outputStack.length < 2){
				throw "unvalid stack length";
			}
			var sec = outputStack.pop();
			var fir = outputStack.pop();

			outputStack.push(getResult(fir, sec, cur));
		}
	}

	if(outputStack.length != 1){
		throw "unvalid expression";
	}else{
		return outputStack[0];
	}
}

6. 결론

역폴란드 표기법은 처음 접할 때는 익숙하지 않지만, 익숙해지고 나면 다양한 우선순위와 우선순위가 있는 중위 표기법과 달리 아이디어가 실제로는 매우 간단하다는 것을 알게 될 것입니다. 괄호, 논리가 특히 번거롭지만 역 폴란드 표기법이 더 간결하고 우선 순위를 전혀 고려할 필요가 없으며 상황을 방해하는 괄호, 대괄호 및 중괄호가 필요하지 않습니다.