ホームページ >テクノロジー周辺機器 >AI >清華ヤオクラスの学部生が2作連続で論文を発表、10年間で最大の改善:行列乗算は理論上の最適値に近づいた
清華ヤオクラスの学部生が2作連続で論文を発表、10年間で最大の改善:行列乗算は理論上の最適値に近づいた
- 王林転載
- 2024-03-08 21:52:02962ブラウズ
コンピュータ科学者は、「隠れた非効率」を排除することで、大規模な行列をこれまでよりも高速に乗算する新しい方法を考案しました。
行列乗算は、多くの GPU オペレーターの基本演算として、ハイパフォーマンス コンピューティングで重要な役割を果たし、AI などのアプリケーションの重要なコンポーネントでもあります。アルゴリズム自体は比較的単純ですが、高速化を実現するために長年にわたってアルゴリズムを最適化する努力が行われてきました。ただし、最適化の範囲はある程度制限されています。
Quantum Magazine の最新号で、行列の乗算を高速化できる 2 つの論文を見つけました。これら 2 つの論文の執筆には、清華大学八尾クラスの学部 4 年生が積極的に参加し、この分野のアルゴリズム改善に新たな展望をもたらしました。
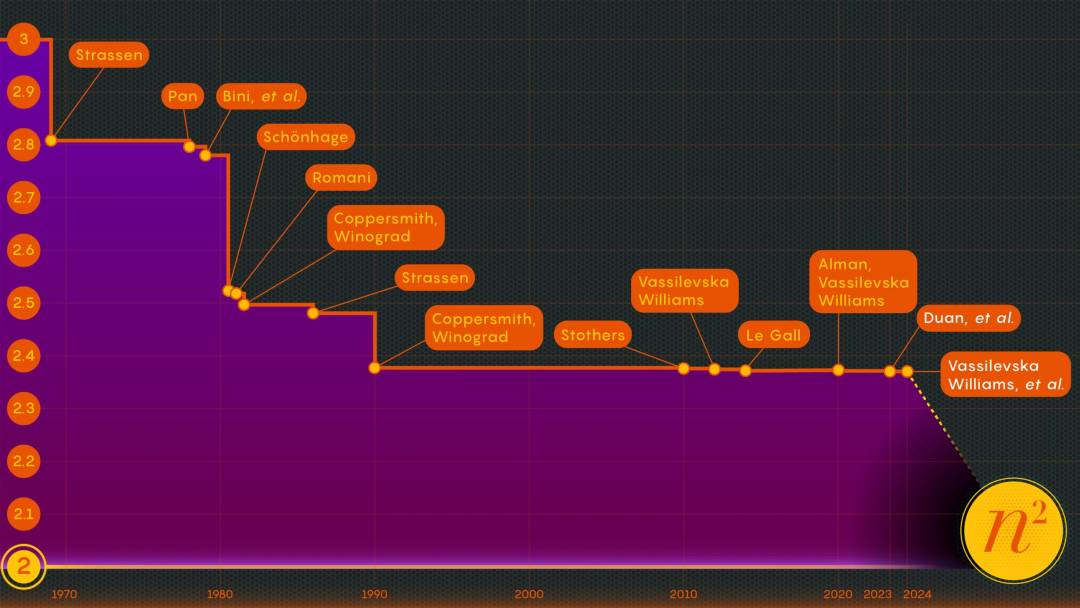
行列乗算の改善に新たな「特異点」が現れる
コンピュータ科学者は、非常に要求の厳しい人々の集団です。彼らが追求するのは、問題を解決するだけではなく、最も効率的な方法で目標を達成することです。
行列や数値配列の乗算を例に挙げてみましょう。1812 年、フランスの数学者ジャック フィリップ マリー ビネは、今日でも学生に教えられている一連の基本的な規則を提案しました。この一連のルールは広く使用されていますが、近年、一部の数学者がプロセスを簡素化し、スピードアップする方法を発見しました。




############### ################################################ ################################################ フランスの数学者ジャック・フィリップ・マリー・ビネ。 ############現在、行列乗算プロセスの高速化は、数学とコンピューター サイエンスの交差点となっています。研究者たちはこのプロセスの改善に取り組んできましたが、ここ数十年の進歩は限られています。名古屋大学のコンピューター科学者フランソワ・ル・ガル氏は、1987 年以降、行列乗算の数値的改善は遅く、達成が困難であると指摘しています。彼は、現在の状況では行列乗算の効率をさらに向上させるには大きな課題に直面しており、さらなる革新と画期的な進歩が必要であると考えています。困難にもかかわらず、科学者たちは行列乗算の計算速度と効率を向上させる新しい方法と技術を見つけることを期待して、ブレークスルーを求めて今も精力的に研究を続けています。これは、行列乗算の最適化が依然として難しいテーマであり、この長期的な問題を最近解決するには、清華大学の Ran Duan 氏と Renfei Zhou 氏、カリフォルニア大学バークレー校の Honxun Wu 氏の共同の努力が必要であることを示しています。既存の問題について調査し、その研究結果は 87 ページの論文で詳細に紹介されています。ル・ガール氏はこれら 3 人の研究者の研究を高く評価し、改善は比較的小さいものの、前例のない概念的な進歩であると信じていました。 ######この論文は、コンピューターサイエンス分野のトップカンファレンスであるFOCS 2023に採択されました。 ###############Paper v1 は 2022 年 10 月に、v5 は 2023 年 11 月にリリースされる予定です。論文アドレス: https://arxiv.org/abs/2210.10173###### その中で、Duan Ran は清華大学学際情報研究所の准教授であり、主な研究方向はグラフ理論アルゴリズム、データ構造です。 、およびコンピューティング理論。 Honxun Wu は、カリフォルニア大学バークレー校の博士課程 2 年生で、清華大学 Yao クラスの卒業生です。 ######Zhou Renfei は、清華大学の 2020 年度ヤオ クラスの学部上級生で、理論コンピューター サイエンス (TCS) を専攻しています。彼は主に (簡潔な) データ構造と高速行列乗算に取り組んでおり、ストリーミング アルゴリズム、ゲーム理論、オンライン アルゴリズムなどの TCS の他の分野にも幅広い関心を持っています。 ######以前、Zhou Renfei は理論コンピューターサイエンスのトップカンファレンスである FOCS/SODA で多くの論文を発表していました。 ################3 人の研究者による論文は、これまで知られていなかった潜在的な改善源を明らかにし、それらはすでに実を結んでいます。 2024 年 1 月に出版された 2 番目の論文 (これも周仁飛との共著) はこれに基づいて構築されており、行列の乗算をさらに強化できる方法を示しています。 ###############論文のアドレス: https://epubs.siam.org/doi/10.1137/1.9781611977912.134###### ハーバード大学の理論コンピューター科学者 William Kuszmaul 氏が次のように回答しました。これは大きな技術的進歩であり、ここ 10 年以上で見た行列乗算の最大の改善であると述べています。 #########行列乗算で改善すべき問題点######
行列の乗算は難解な問題のように思えるかもしれませんが、基本的な計算操作です。これは、より鮮明なコンピュータ グラフィックスの表示からネットワーク理論における物流問題の解決に至るまで、さまざまなタスクで人々が毎日使用するアルゴリズムのほとんどに組み込まれています。コンピューティングの他の分野と同様に、スピードが最も重要です。たとえ小さな改善であっても、最終的には必要な時間、計算能力、費用を大幅に削減できる可能性があります。しかし今のところ、理論家たちは主に、プロセスがどれだけ速く進むかを解明することに興味を持っている。
2 つの n×n 行列を乗算する従来の方法 (つまり、最初の行列の各行の数値と 2 番目の行列の各列の数値を乗算) では、n³ 個の独立した演算 (乗算演算) が必要です。 2 x 2 行列の場合、これは 2³、つまり 8 回の乗算を意味します。
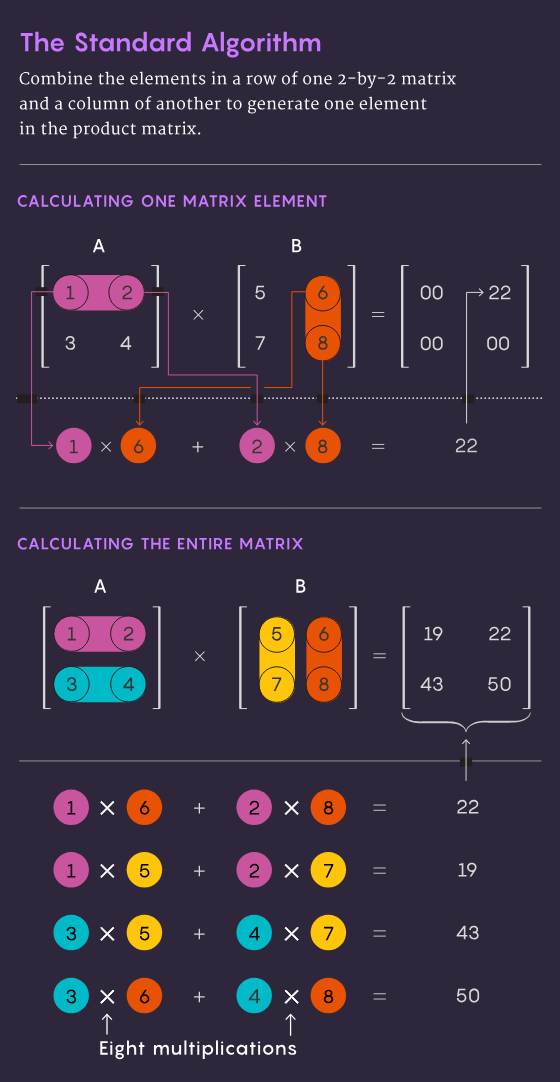
1969 年、数学者の Volker Strassen は、わずか 7 つの乗算ステップと 18 の加算ステップで 2×2 行列を完成できる、より洗練された方法である乗算演算を発見しました。 2 年後、コンピューター科学者のシュムエル ウィノグラードは、7 ステップの乗算が 2×2 行列の絶対最小値であることを示しました。
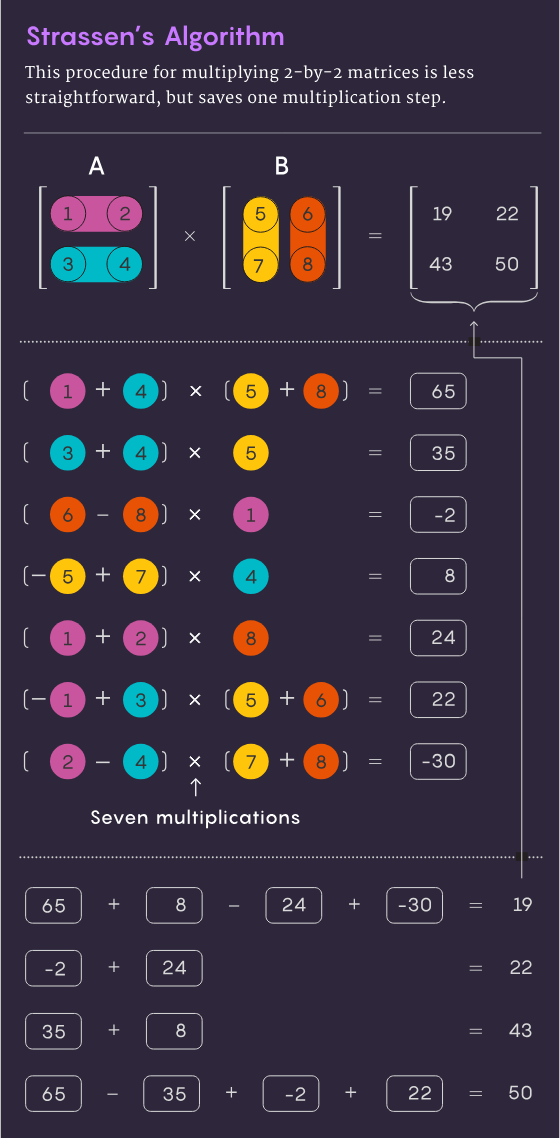
Strassen は同じアイデアを使用して、すべての大きな n×n 行列も n3 ステップ未満で乗算できることを示しました。この戦略の重要な要素には、分解と呼ばれる手順が含まれます。これは、大きな行列を小さな部分行列に分解することで、最終的には 2×2 または 1×1 (単一の数値) まで小さくなる可能性があります。
巨大な配列を小さな部分に分割する理由は非常に単純で、MIT のコンピューター科学者であるバージニア・ヴァシレフスカ・ウィリアムズ氏は次のように述べています。人間が考えるべき最も優れたアルゴリズム。」 3 行 3 列の行列ですら、まだ完全には解決されていません。 「ただし、小さな行列用に開発された高速アルゴリズムを使用して、より大きな行列用の高速アルゴリズムを取得することはできます。」
研究者らは、速度の鍵は乗算ステップの数を減らし、指数を移動することにあると判断しました。 n3(従来法)から可能な限り下げます。可能な最小値 n² は、基本的に、答えを書くのにかかる時間です。コンピューター科学者は、この指数を Ω または ω と呼びます。 nω は、n が大きくなるにつれて 2 つの n×n 行列を正常に乗算するために必要な最小ステップ数です。 2024年1月の論文の共著者でもある周仁飛氏は、「この研究の焦点は、2にどれだけ近づくことができるか、理論的に達成できるかどうかを確認することだ」と述べた。 ## レーザー法
1986 年、ストラッセンは行列乗算のレーザー法を導入し、さらなる大きな進歩を遂げました。 Strassen はこれを使用して 2.48 という ω の上限を決定しました。この方法は大規模な行列乗算の 1 ステップにすぎませんが、研究者は常に改良しているため、最も重要なステップの 1 つです。
1 年後、Winograd と Don Coppersmith は、レーザー法を完全に補完する新しいアルゴリズムを導入しました。このツールの組み合わせは、行列乗算の高速化に関するその後のほぼすべての研究で使用されました。 ここでは、これらのさまざまな要素がどのように組み合わされるかを確認する簡単な方法を示します。 2 つの大きな行列 A と B から始めて、それらを乗算してみましょう。まず、それらを多くの小さな部分行列 (チャンクと呼ばれることもあります) に分割します。次に、これらのブロックを処理し、最終的に組み立てるためのガイドとして、Coppersmith と Winograd のアルゴリズムを使用できます。 「それは、何を掛けるべきか、何を加えるべきか、そしてどの要素が積行列Cのどこにあるかを教えてくれます。これは、AとBからCを構築するための単なる『レシピ』です。」とヴァシレフスカ・ウィリアムズ氏は言いました。 ただし、問題があります。共通の要素を含むブロックが取得される場合があります。これらの共通要素を保持することは、これらの要素を 2 回カウントすることと同じであるため、ある時点でこれらの重複を削除する必要があります。研究者らは、ブロックが含まれていたブロックを「強制終了」することで、つまりコンポーネントをゼロに設定して計算から除外することで、この問題を解決しました。 ## virginia vassilevskaウィリアムズは、マトリックス増殖の新しい方法を改善したチームの一部であり、現在利用可能な最速の方法を思いつきました。
## virginia vassilevskaウィリアムズは、マトリックス増殖の新しい方法を改善したチームの一部であり、現在利用可能な最速の方法を思いつきました。 ここで、ストラッセンのレーザー法が最終的に登場します。 「レーザー法は通常非常に効果的であり、重なり合うサブブロックを除去する良い方法が見つかることがよくあります」とル・ガル氏は語った。レーザーがすべての重なりを除去した後、最終的な製品マトリックス C を構築できます。 これらのさまざまな手法を組み合わせると、少なくとも理論的には、合計の乗算をできるだけ少なくして 2 つの行列を乗算するアルゴリズムが得られます。レーザー法は実際の応用を目的としたものではなく、行列の乗算に関する理想的な考え方にすぎません。 Zhou Renfei 氏は、「私たちはこの方法をコンピューターで実行したことがありません。私たちはそれを分析します。」 ω の 10 年以上で最大の改善につながったのは、この分析です。 発見された「隠れた損失」 Duan Ran、Zhou Renfei、Hongxun Wu による最初の論文「非対称ハッシュによる高速行列乗算」で、彼らは を示しました。 Strassen のアルゴリズムのプロセスを大幅に加速できます。これはすべて、彼らが「隠れた損失」と呼ぶ概念のおかげです。周仁飛氏は、この概念は以前の分析で深く隠されており、不用意に多くのブロックを削除しすぎた結果だと述べた。 レーザー方式は、重複するブロックをガベージとしてマークし、処理のスケジュールを設定することで機能しますが、他のブロックは価値があると見なされ、保存されます。ただし、選択プロセスはある程度ランダムです。実際、ゴミとしてマークされたブロックは、最終的には役立つ可能性があります。 これはまったく驚くべきことではありませんが、Duan Ran のチームは、多くのランダムな選択を調査することにより、レーザー法が体系的にブロックの価値を過小評価しているため、より多くのブロックを保存し、破棄するブロックを少なくする必要があると判断しました。そして、よくあることですが、無駄が減れば効率も上がります。 Duan Ran のチームのアプローチについて、Le Gall 氏は、「より多くのブロックを重複させることなく保持できる。このアプローチにより、より高速な行列乗算アルゴリズムが実現される。」 この種の損失が存在した後、これが証明されました。 , Duan Ran 氏のチームは、ブロックにレーザーでマーキングする方法を修正し、無駄を大幅に削減しました。彼らは、ω の新しい上限を約 2.371866 に設定しました。これは、2020 年にジョシュ アルマンとヴァシレフスカ ウィリアムズによって設定された上限 2.3728596 を上回る改善です。 これは、上限を 約 0.001 下げる小さな変更のように見えるかもしれませんが、科学者が 2010 年以降に確認した最大の改善です 。比較すると、ヴァシレフスカ・ウィリアムズとアルマンの2020年の成績は、前回の成績からわずか0.00001改善しただけだ。 もちろん、研究者にとって最もエキサイティングなことは、長く続かなかった新記録そのものだけではありませんでした。実際、この論文は、これまでまったく気づかれていなかった、改善のための新たな道を明らかにしています。 ル・ガール氏は、誰もが40年近く同じレーザー法に頼ってきたと語った。 Duan Ran を含む 3 人の研究者による論文の出現により、私たちはさらに改善できるでしょう。 したがって、Zhou Renfei 氏が共著した 2024 年 1 月の論文では、この新しい手法が改良され、隠れた損失がさらに削減されました。彼らは ω の上限をさらに引き上げ、2.371552 まで下げました。 研究者らは、同じ方法を使用して、グラフ理論、機械学習、その他の分野で広く使用されている方形 (n×m) 行列の乗算プロセスを改善しました。応用。 これらの方向に沿ってさらなる進展が見られることはほぼ確実ですが、限界もあります。 2015年に、Le Gallと2人の共著者は、現在の方法、つまりレーザー法をCoppersmithとWinogradの方法と組み合わせた場合、2.3078未満のωを取得できないことを示しました。 ル・ガル氏は、「さらに改善するには、カッパースミスとウィノグラードのオリジナルの方法を改善する必要があります。これは1987年以来ほとんど変わっていません。」しかし、これまでのところ、これより良い方法を思いついた人はいません。まだ。もしかしたら全くそうではないかもしれません。 Zhou Renfei 氏は次のように述べています。「ω を改善することは、実際にはこの問題を理解することの一部です。この問題をよく理解できれば、より良いアルゴリズムを設計できます。しかし、この古くからある問題に対する人々の理解はまだ不明確です。予備段階。」 元のリンク: https://www.quantamagazine.org/new-breakthrough-brings-matrix-multiplication -理想に近づく-20240307/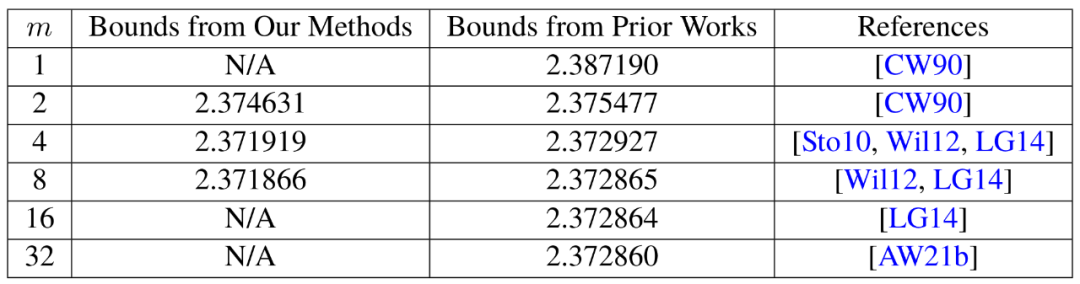
以上が清華ヤオクラスの学部生が2作連続で論文を発表、10年間で最大の改善:行列乗算は理論上の最適値に近づいたの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

