多重線形回帰モデルの概念と応用の詳細な分析

重線形回帰は線形回帰の最も一般的な形式であり、単一の応答変数 Y が複数の予測子変数とどのように線形関係を示すかを説明するために使用されます。

重回帰を使用できるアプリケーションの例:

住宅の販売価格は、場所、寝室とバスルームの数、建設年、敷地面積、もっと。

2. 子供の身長は、母親の身長、父親の身長、栄養および環境要因によって異なります。

重線形回帰モデルのパラメーター

k 個の独立した予測子変数 x1、x2...、xk と応答変数 y をもつ重線形回帰モデルを考えます。

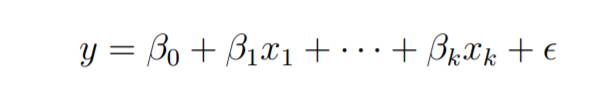
k 1 個の変数に対して n 個の観測値があり、n 個の変数が k より大きいはずだとします。

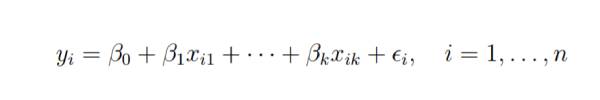
最小二乗回帰の基本的な目標は、超平面を (k 1) 次元空間に当てはめて、残差の二乗和を最小化することです。

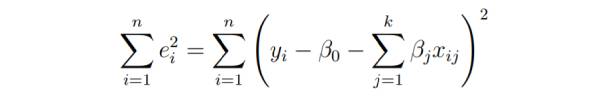
#モデル パラメーターを微分する前に、それらをゼロに設定し、パラメーターが満たす必要がある最小二乗正規方程式を導出します。

これらの方程式は、ベクトルと行列を利用して定式化されます。

#線形回帰モデルは次のように記述されます:

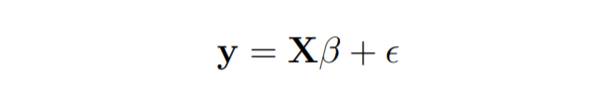
# #Online 線形回帰では、最小二乗パラメータ推定 b

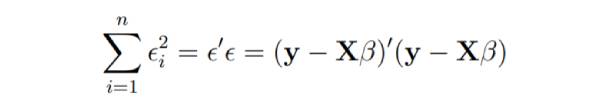
列が変化することを想像してください。二乗残差の合計を最小化する「最良の」 b を見つけたいと考えています。

可能な最小の二乗和はゼロです。

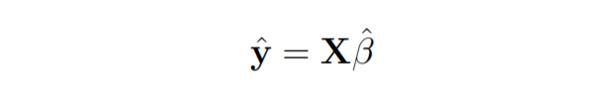#ここで、y は推定された応答ベクトルです。

#このコードは、データセット data2

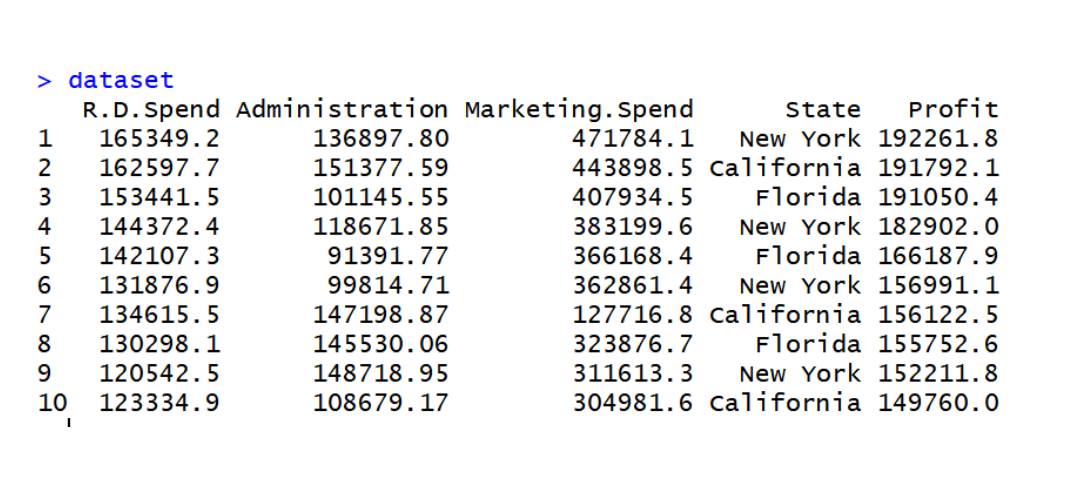
data2 データセット

dataset=read.csv('data2.csv')
dataset$State=factor(dataset$State,
levels=c('New York','California','Florida'),
labels=c(1,2,3))
dataset$State

## に対して重回帰を実装します。 #rree

以上が多重線形回帰モデルの概念と応用の詳細な分析の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。