ホームページ >テクノロジー周辺機器 >AI >データ サイエンティストが 95% の時間使用する 11 の基本ディストリビューション
データ サイエンティストが 95% の時間使用する 11 の基本ディストリビューション
- 王林転載
- 2023-12-15 08:21:251246ブラウズ
前回の「データ サイエンティストが 95% の時間使用する 11 個の基本チャート 」に続き、今日はデータ サイエンティストが 95% の時間使用する 11 個の基本チャートを配布します。これらの分布をマスターすることで、データの性質をより深く理解し、データ分析や意思決定の際により正確な推論や予測を行うことができます。

1. 正規分布
正規分布はガウス分布とも呼ばれ、連続タイプの確率分布です。平均(μ)を中心、標準偏差(σ)を幅とした対称な釣鐘型の曲線を持ちます。正規分布は、統計学、確率論、工学などの多くの分野で重要な応用価値があります。
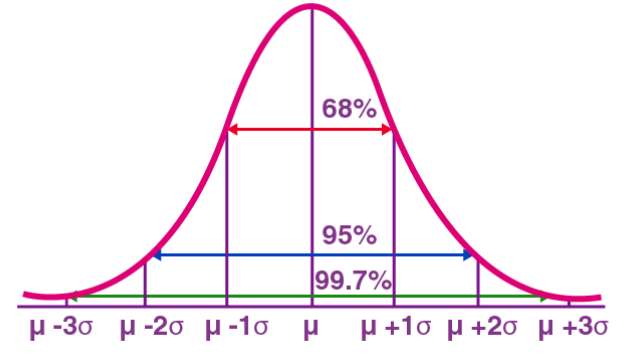
正規分布の確率密度関数は次のように表すことができます。
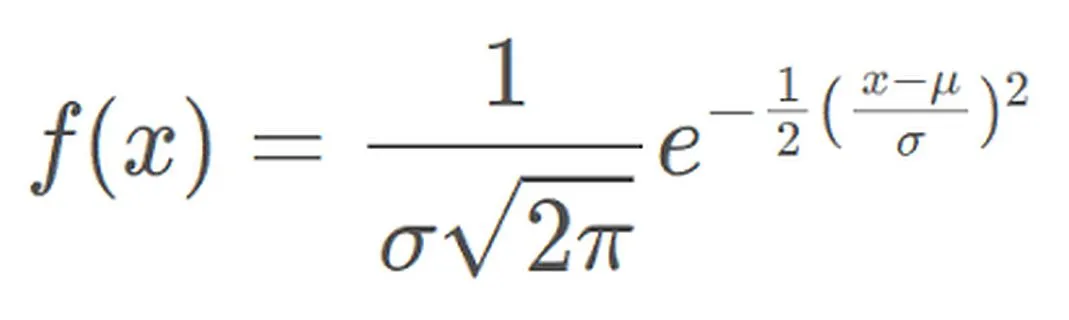
確率密度関数は次のように表されます。指定された値 x 近くの単位間隔内の正規分布する確率変数の値の確率密度。このうちμは平均値、σは標準偏差を表します
正規分布は実務で広く使われています。たとえば、人間の身長と体重の分布は正規分布に近似します。さらに、テストの得点は多くの場合正規分布しており、高得点と低得点を獲得する人は少なく、中間の得点を獲得する人が多くなります。この分布モデルは多くの分野で重要な応用価値があります
2. ベルヌーイ分布
ベルヌーイ分布 (ベルヌーイ分布) は、2 つの可能な結果のみを含む単一のランダム化試験を記述するために使用される離散確率分布です。ベルヌーイ試行には、表か裏、成功か失敗、はいかいいえなどがあります。たとえば、コインを投げたり、製品が認定されているかどうか、誰かが特定の製品を購入するかどうかをテストするなどです。
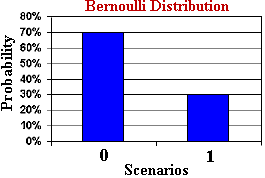
ベルヌーイ分布の確率質量関数は次のとおりです。
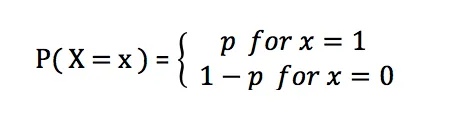
ベルヌーイ分布では、p は成功を表します。確率の範囲は次のとおりです。 0から1。 p が 0.5 に等しい場合、ベルヌーイ分布は一様分布に近づきます。
実際のベルヌーイ分布の適用: たとえば、二項分布は、ベルヌーイ分布の n 回の独立した反復実験です。
3. 二項分布
二項分布 (Binomial Distribution) は、n 回の独立した反復実験における成功数の確率分布を記述するために使用される離散確率分布です。各トライアルには、成功 (1 として記録) または失敗 (0 として記録) の 2 つの結果しかありません。成功の確率は p 、失敗の確率は 1-p です。
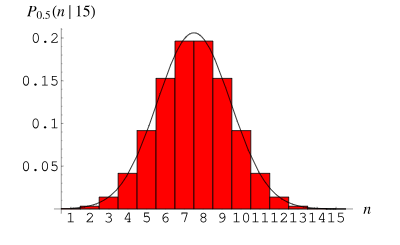
二項分布の確率質量関数は次のように表現できます。
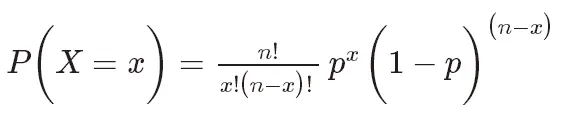
このうち、P(X= k) は成功数が k である確率を表し、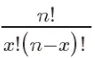 は組み合わせ数で、n 回の試行から選ばれた k 個の成功した組み合わせの数を示します。 p は成功の確率で、範囲は 0 から 1 です。 n は試行回数です。
は組み合わせ数で、n 回の試行から選ばれた k 個の成功した組み合わせの数を示します。 p は成功の確率で、範囲は 0 から 1 です。 n は試行回数です。
二項分布は実際に広く使用されています。たとえば、医学研究では、二項分布を使用して、特定の治療を受けた患者の成功率を計算できます。エンジニアリング分野では、二項分布を使用して、生産プロセス中の製品の合格率を評価できます。これらは、実際のアプリケーションにおける二項分布の重要な例です。
4. ポアソン分布
ポアソン分布 (ポアソン分布) は、イベント数の固定確率分布を記述するために使用される離散確率分布です。時間内に起こること。ポアソン分布は、イベントが独立しており、一定の平均レートで発生する状況に適しています。
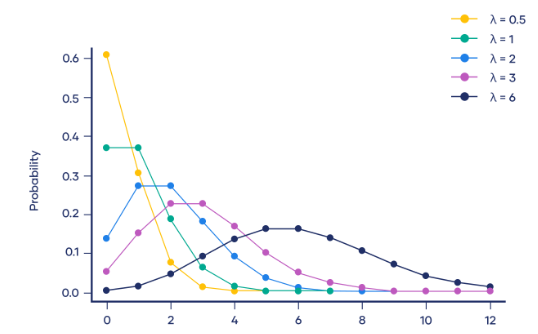
ポアソン分布の確率密度関数は次のとおりです:
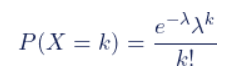
ここで、P(X=k)は一定期間内にイベントがk回発生する確率を表し、λはイベントの平均発生率、つまり単位時間当たりに発生するイベントの平均数を表します。 e は自然定数で、2.718 にほぼ等しくなります。 k は発生するイベントの数を表します
ポアソン分布は実際に広く使用されています。たとえば、コールセンターでは、1 分あたりの通話数はポアソン分布とみなすことができます。 1 分あたりの呼び出し数は
5 です。 指数分布
指数分布 (Exponential Distribution) は、一定期間内にイベントが発生する確率を記述するために使用される連続確率分布です。 。指数分布は、イベントが互いに独立しており、一定の平均レートで発生する状況に適しています。
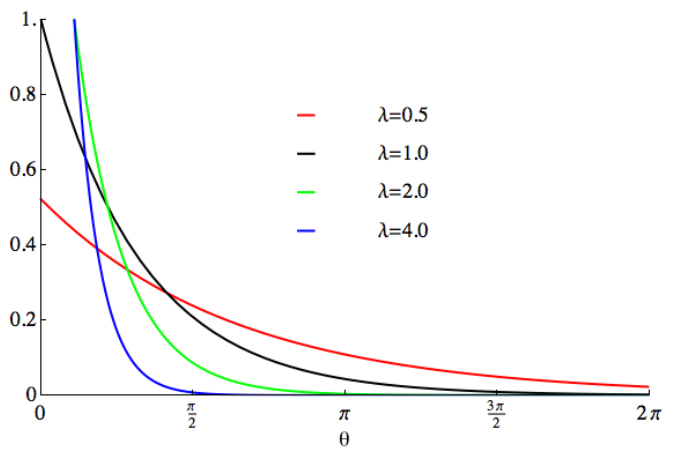
指数分布の確率密度関数は次のとおりです。
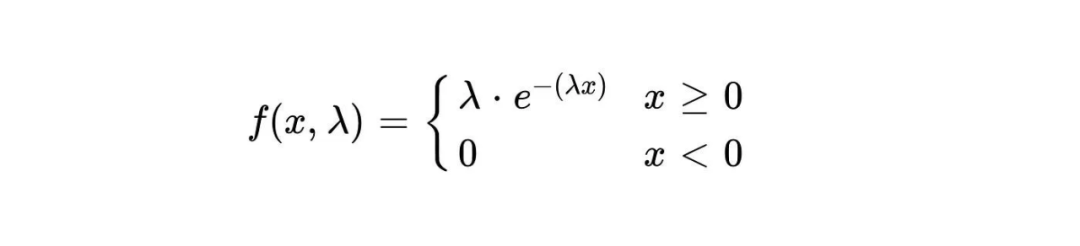
指定された環境内で発生するイベントの確率密度時間xはf(x,λ)で表されます。 λはイベントの平均発生率、つまり単位時間当たりに発生するイベントの平均数を表す。 e は自然定数で、ほぼ 2.718
指数分布は現実に多くの用途があります。たとえば、放射性崩壊では、放射性原子核の崩壊時間は指数関数的に分布していると見なすことができます。これは、減衰時間の確率分布が指数関数に従うことを意味します。平均減衰時間は、指数関数 λ
6 のパラメーター λ に対応します。ガンマ分布
ガンマ分布は、特定の環境内でイベントが発生する確率を記述するために使用される連続確率分布です。時間 。これは、イベントが互いに独立しており、平均発生率が一定のままである状況に適しています。
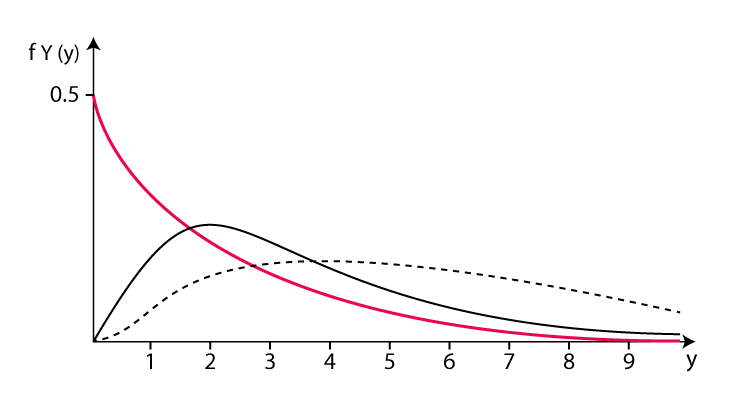
ガンマ分布の確率密度関数は次のとおりです:
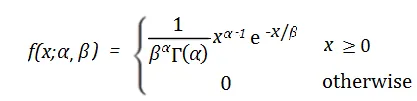
ここで、f(x) は、特定の時間 x 内に発生するイベントの確率密度を表します。 α と β は、ガンマ分布の形状パラメータとレート パラメータです。 α はガンマ分布の形状を決定するために使用され、その値の範囲は 0 から正の無限大までです。 βはイベントの平均発生率、つまり単位時間当たりに発生するイベントの平均数を表し、値の範囲は0から正の無限大までとなります。 e は自然定数で、ほぼ 2.718
ガンマ分布の実際への応用: たとえば、放射性崩壊: 放射性崩壊では、放射性原子核が崩壊するまでの時間をガンマ分布とみなすことができ、平均減衰時間は β/α です。
7. ベータ分布
ベータ分布は、一連の値における成功回数の確率分布を記述するために使用される連続確率分布です。これには、成功確率の期待値 (平均) と標準偏差 (標準偏差) を表す 2 つのパラメーターがあります。
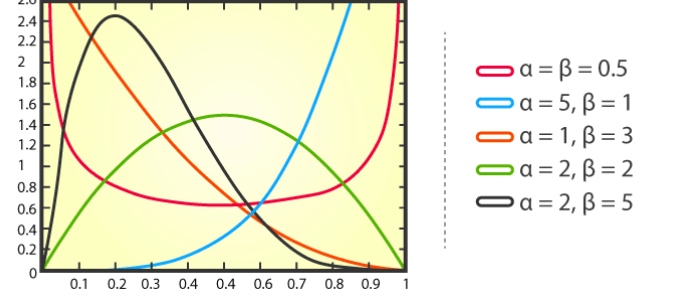
ベータ分布の確率密度関数は次のとおりです。
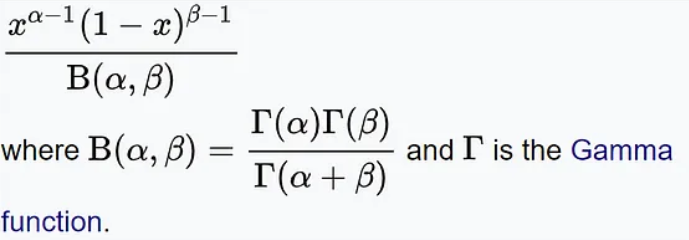
このうち、x は数を表します。成功すると、α と β はそれぞれ分布の形状パラメータを表します
ベータ分布は多くの実際的な問題に応用できます。たとえば、遺伝子編集では、研究者はベータ分布を使用して、遺伝子編集技術が特定の標的部位の編集に成功する確率を予測することがあります。金融分野では、ベータ分布は資産価格の変動性を説明したり、投資ポートフォリオの期待収益を計算したりするために使用できます。
8. 一様分布
一様分布は確率です。分布。特定の間隔内で均等に分布する一連の値を表すために使用されます。一様分布には、離散一様分布と連続一様分布の 2 種類があります。
離散一様分布: 離散確率変数の場合、X は離散一様分布に従うと言います。連続一様分布: 連続確率変数 X の確率密度関数が f(x) = 1/(b-a) であるとき、
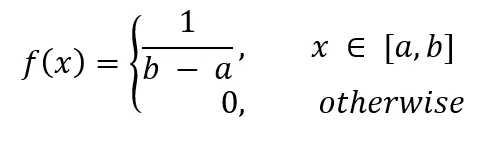 #一様分布の特徴は、与えられた範囲内で間隔に応じて、すべての値が出現する可能性は同じになります。たとえば、公平なコインを投げた場合、表と裏の確率は 1/2 であり、これは一様分布です。
#一様分布の特徴は、与えられた範囲内で間隔に応じて、すべての値が出現する可能性は同じになります。たとえば、公平なコインを投げた場合、表と裏の確率は 1/2 であり、これは一様分布です。
9. 対数正規分布
対数正規分布 (対数正規分布) は連続確率分布であり、確率変数の対数が正規分布に従うという特徴があります。言い換えれば、確率変数 X の対数 ln(X) が正規分布に従う場合、確率変数 X は対数正規分布に従うことになります。
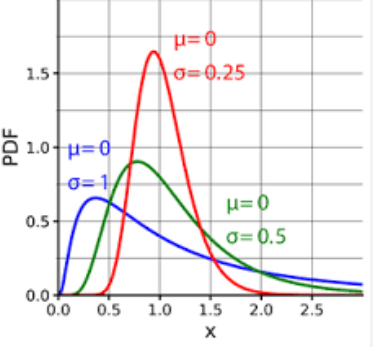
対数正規分布の確率密度関数は次のように表現できます。
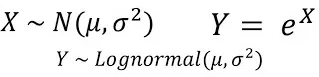
ここで、μ は対数正規分布です。は対数正規分布の平均、σ は対数正規分布の標準偏差です。
対数正規分布は、金融 (株価、利回りなど)、生物学 (成長率など)、経済学 (消費者支出など) など、多くの実際の応用において非常に重要です。 。
10. T 分布
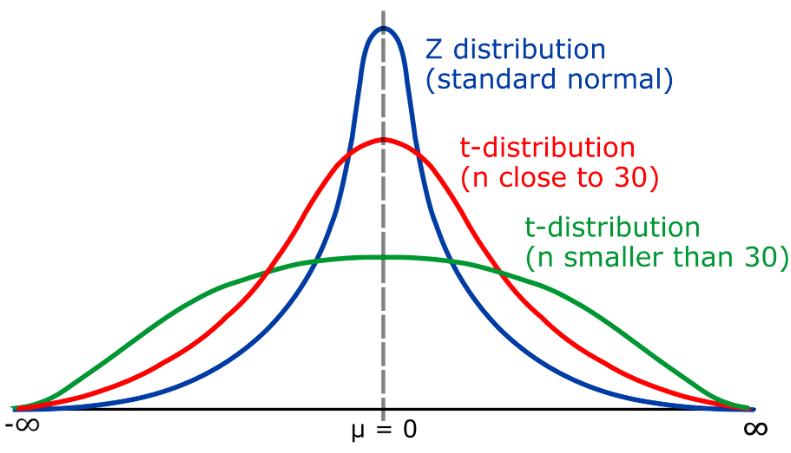
T 分布は連続確率分布であり、主にサンプルが小さい状況における平均値の分布を記述するために使用されます。 t 分布は正規分布に似ていますが、自由度 (k) に応じて尾部が左右に伸びる可能性があります。 t 分布は、サンプル平均と母集団平均の間の有意差を評価するための仮説検定など、統計的推論で広く使用されています。
t 分布の期待値と分散は次のとおりです。
E(t)=0
書き換える内容は、 : Var( t)=k/(k-1)
t 分布の自由度 (k) は、サンプル サイズ (n) と母集団標準偏差との関係を表します。 k > 30 の場合、t 分布は正規分布に近くなります。k が 1 に近い場合、t 分布はコーシー分布 (コーシー分布) になります。
実際のアプリケーションでは、サンプル サイズが大きい場合 ( n>30 )、正規分布は仮説検定に使用でき、z 統計量は信頼区間を確立するために使用できます。ただし、サンプル サイズが小さい場合 (n
11. ワイブル分布
ワイブル分布 (ワイブル分布) は連続確率分布です。
ワイブル分布の確率密度関数は次のとおりです。
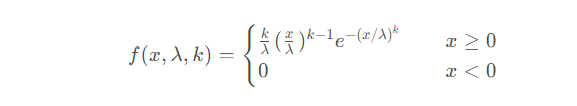
ワイブル分布では、x は確率変数とみなされ、λ はスケールと呼ばれます。パラメータ (scale)、k は形状パラメータ (shape) です。ウェーバー分布に関する限り、k が 1 に等しい場合、指数分布になります。 λ が 1 に等しい場合、これは最小化されたワイブル分布です。
以上がデータ サイエンティストが 95% の時間使用する 11 の基本ディストリビューションの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

